一个求幂指函数的极限定理及其应用

刘元宗，黄　诚

（广东外语外贸大学南国商学院，广州510545）

一个求幂指函数的极限定理及其应用

刘元宗，黄诚

（广东外语外贸大学南国商学院，广州510545）

给出了一个关于求幂指函数极限的定理。通过该定理，把求幂指函数的极限转化为求两个函数乘积的极限，从而避免了在应用第二重要极限时“凑指数”的繁琐过程。给出的例子说明了这种方法的简洁性。

幂指函数；重要极限；凑指数；应用

幂指函数是微积分中一类重要的函数，其特点是底数和指数都带有自变量。通常情况下，幂指函数表示为f( x)g( x)，当x发生变化时，底数和指数都发生变化。比如，就是这样的函数。

1　幂指函数极限定理

引理1：若在x的某个变化过程中，有limϕ(x) =0，则有。

证明：令ϕ(x)=t，则由limϕ(x )=0可知t→0，于是由可得，

引理2［2］：若在x的某个变化过程中，有limf( x) =A >0和limg( x)=B，则有limf( x)g( x)=AB。

证明：因为limf( x)=A>0，由极限的保号性可知，在极限点的某个领域内，有f( x)>0，于是由对数恒等式可得f( x)g( x)=eg( x)lnf( x )。令u( x)=g( x)lnf( x)，则eu( x)为连续函数。

由于eu(x)是连续函数，故有limeu( x)=elimu( x )，于是，有limf( x)g( x)=lim eg( x)lnf(x)=elimg( x)lnf(x)=eBlnA=AB。

定理1：若在x的某个变化过程中，limϕ(x)=0，limf( x)=∞，limϕ(x) f( x)=a，则有

证明：因为在x的某个变化过程中，有limϕ(x )=0，limf( x)=∞，所以，有

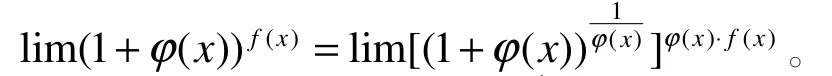
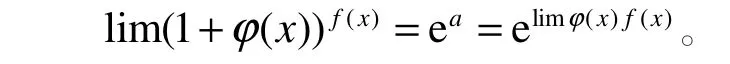
2　幂指函数极限定理的应用

2.1求幂指函数极限的步骤

在x的某个变化过程中，若函数ϕ(x)的极限为零，f( x)的极限为无穷大，则在求“1加无穷小的无穷大次幂”形式(1+ϕ(x) )f( x)函数的极限时，可按以下步骤计算极限：1）将极限式化成lim(1+ϕ(x) )f( x)=elimϕ(x) f( x)的形式；2）求极限limϕ(x) f( x)；3）求lim(1+ϕ(x ))f( x)。

当幂底的形式不是“1加无穷小”时，要先把它化为“1加无穷小”的形式1+ϕ(x)后，再应用式（1）求极限［3］。

2.2求幂指函数极限的例子

例1［4］：求极限

解：本例的幂底x不是“1加无穷小”的形式，必须把它化为x=1+(x−1)后，才能运用式（1）求极限。

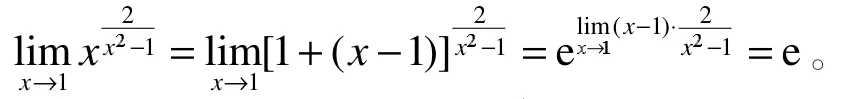
解：本例的幂底为1− sin 3x ，不是“1加无穷小”的形式，需要先化为1+(−sin 3x)，再应用式（1）求解。令，则有

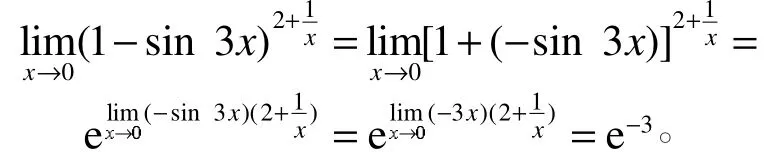
为了避免在指数上进行极限运算，例3的求极限过程也可以表示为如下形式：

例4［4］：求极限

从以上几个求幂指函数极限的例子可以看出，把幂指函数化为“1加无穷小的无穷大次幂”形式，求极限过程将变得简单、快捷，学生易于掌握。

3　结束语

笔者给出了一个幂指函数的极限定理，通过该定理，可以把求幂指函数的极限转化为求两个函数乘积的极限，避免了应用第二重要极限时“凑指数”的繁琐，化解了教学难点。

在求幂指函数极限的教学过程中，该定理给出的方法具有一定的指导和借鉴意义。

［1］隋如彬，吴刚，杨兴云.微积分：经济类［M］.2版.北京：科学出版社，2014：60-61.

［2］朱来义.微积分［M］.北京：高等教育出版社，2009：50.

［3］张建梅，马庆华，席敏，等.经济数学：微积分［M］.北京：科学出版社，2012：41.

［4］吴赣昌.微积分［M］.北京：中国人民大学出版社，2009：54-55.

【责任编辑王云鹏】

A Theorem of Calculating Limit of Power Exponential Function and Its Application

LIU Yuanzong，HUANG Cheng
（South China Business College，Guangdong University of Foreign Studies，Guangzhou 510545，China）

A theorem of calculating limit of power exponential function was given in this paper.By this theorem，the limit of power exponential function was transformed into the product's limit of two functions so that the complex steps of making up index were avoided by means of the second important limit.The given examples have illustrated the conciseness of using this theorem to calculate limit of power exponential function.

power exponential function；important limit；make up index；application

G642.0

A

2095-7726（2016）03-0065-02

2015-09-04

广东省教育厅高等教育教学改革项目（粤教高函〔2015〕173号）

刘元宗（1947-），男，河南巩义人，教授，研究方向：初等数论和数学方法论。