σ星座设计与仿真

张雅声，　莫　薇

(1. 装备学院 航天装备系， 北京 101416;　2. 北京卫星制造厂， 北京 100094)



σ星座设计与仿真

张雅声1，莫薇2

(1. 装备学院 航天装备系， 北京 101416;2. 北京卫星制造厂， 北京 100094)

σ星座作为一种具有独特星下点轨迹特性的特殊Walker星座类型，有关σ星座设计方法的描述在众多文献中相对缺乏，许多阐述也并不完备。基于此，深入研究了地面轨迹分离数与σ星座构型的关系，建立了σ星座空间几何模型，提出了一种σ星座设计解析方法。通过STK软件仿真验证了该设计方法的可行性，仿真结果表明,σ星座在高轨通信卫星星座和预警卫星星座的设计方面具有巨大的应用前景。

σ星座；Walker星座；星座设计；共轨迹

随着航天技术的不断发展，人类对卫星的需求不断增大，尤其是当单颗卫星已经不能满足对地面区域的覆盖要求时，由多颗功能相同或相近的卫星组成的卫星星座应运而生了。Walker星座就是目前世界上应用最广泛的星座构型[1-6]。Walker星座是一种均匀对称的星座构型，也是全球覆盖或纬度带覆盖最有效的星座构型。Walker星座可以分为星形星座、玫瑰星座、δ星座、σ星座和Ω星座等多种构型，其中δ星座得到了普遍承认和广泛应用，通常称为Walker-δ星座，而σ星座正是δ星座的一个特例。σ星座中所有卫星的星下点沿着一条类似正弦的曲线等间隔分布，具有稳定的地面覆盖特性。在满足同一覆盖要求的前提下，σ星座所需要的卫星数量较少，是一种比较经济的星座构型[7-9]。但是，对于σ星座的设计方法相关资料非常少，目前能够查阅到的主要就是文献[10]369-384中提出的有关σ星座的一些描述，且文献中相关计算公式及其参数的定义不清楚，不具有可操作性。在现有在轨运行的各种卫星星座中，只有俄罗斯GLONASS导航卫星星座采用了σ星座构型，这给其地面测控和管理带来了很大的便利。

本文从Walker星座构型出发，分析地面轨迹分离数与σ星座的关系，研究σ星座的轨道特点，从而提出一种具有可操作性的σ星座设计解析模型，并通过仿真验证该解析模型的实用性。

1　σ星座设计解析模型

1.1Walker星座构型描述

由于σ星座是Walker星座的一种特例，因此，首先需要了解Walker星座中的轨道构型。通常Walker星座构型可以用“N/P/F”来表示，即Walker星座的N颗卫星均匀分布在P个轨道平面上，且这P个轨道平面沿赤道等间隔分布(即沿360°或180°均匀分布)；每个轨道平面上的S颗卫星也是均匀分布的，相邻轨道平面之间卫星的相位差Δf保持不变，用相位因子F表示，即

(1)

(2)

式中，F是0～(P-1)之间的一个整数。

1.2地面轨迹分离数

卫星星座的星下点轨迹条数称为卫星星座的地面轨迹分离数。在N颗卫星组成的Walker星座中，如果卫星均选择回归轨道，那么，该Walker星座的星下点轨迹可能存在以下几种情况：

1) 星座中的每颗卫星都有自己的一条星下点轨迹，则星座有N条星下点轨迹；

2) 星座中相同轨道平面上的卫星重复相同的星下点轨迹，则星座有P条星下点轨迹；

3) 星座中所有卫星重复相同的星下点轨迹，则星座只有一条星下点轨迹。

假设Walker星座N/P/F中的卫星均采用D/L(这里L和D为互质数)特性的准回归轨道[10]369，即卫星在D个恒星日内绕地球L圈以后，它的星下点轨迹开始重复。那么，该Walker星座的地面轨迹分离数EL,D可以由下式确定

(3)

式中，K=H[G,PJ],G=SL+FD,J=H[S,D],S=N/P,H[x,y]表示取x和y的最大公因子。

1.3σ星座构型建模

σ星座中的所有卫星的星下点轨迹沿着一条类似正弦曲线的地面轨迹运动，且各颗卫星的瞬时星下点位置沿着该轨迹等间隔分布，如图1所示。

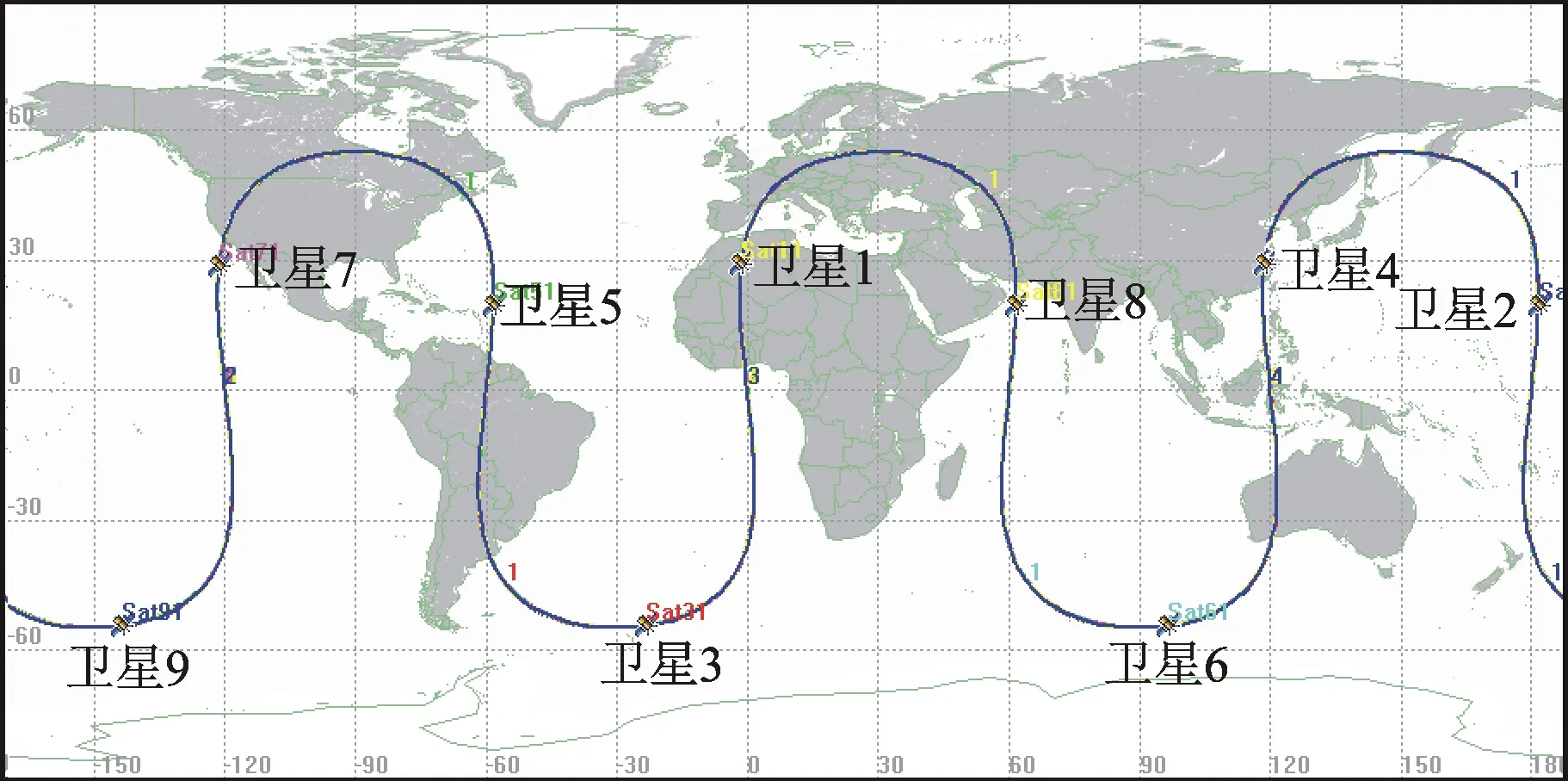
图1　σ星座星下点轨迹示意图

可见，σ星座中的卫星轨道应该均为回归轨道，且地面轨迹分离数为1，即

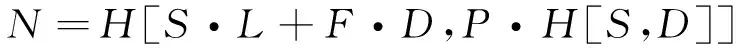
(4)

已知H[x,y]表示取x和y的最大公因子，则有

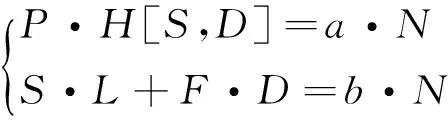
(5)

式中，a、b均为互质的正整数。由于

(6)

可以解得地面轨迹分离数为1的Walker星座必须满足下列关系式

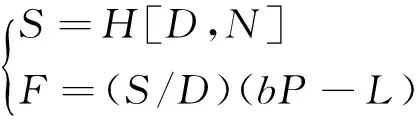
(7)

显然，这是一个D天L圈回归的N/P/F构型的Walker星座。然而，为了保证σ星座中的所有卫星沿着一条类似正弦曲线等间隔分布，它还需要具有如下特点，即

(8)

也就是说，σ星座中的卫星轨道是D天运行(D+1)圈的准回归轨道。因此，σ星座的设计模型为

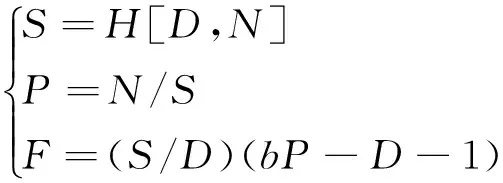
(9)

基于上述关系式，σ星座只需要用(N，D)2个参数就可以表示出Walker星座的参考码N/P/F。

由于σ星座所有卫星的星下点轨迹是一条类似正弦曲线的封闭曲线，且星座中的所有卫星沿该曲线均匀分布。因此，星下点轨迹上顺序相随的2颗卫星之间的相差为

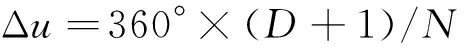
(10)

2　典型σ星座设计仿真

下面基于STK仿真软件[11]，设计一个由9颗卫星组成的σ星座。要求卫星轨道分别采用2天回归和3天回归的准回归轨道，即

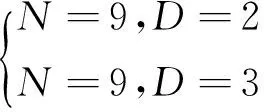
2.1N=9,D=2的σ星座

由于L=D+1，则回归圈数为L=3，利用式(9)可得

已知F为0～(P-1)之间的一个整数，代入验证以后，可得

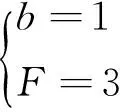
也就是说，(9,2)构型的σ星座所对应的Walker星座构型为9/9/3，轨道参数如表1所示，图2和图3分别是该σ星座的星下点轨迹和三维空间轨道构型。

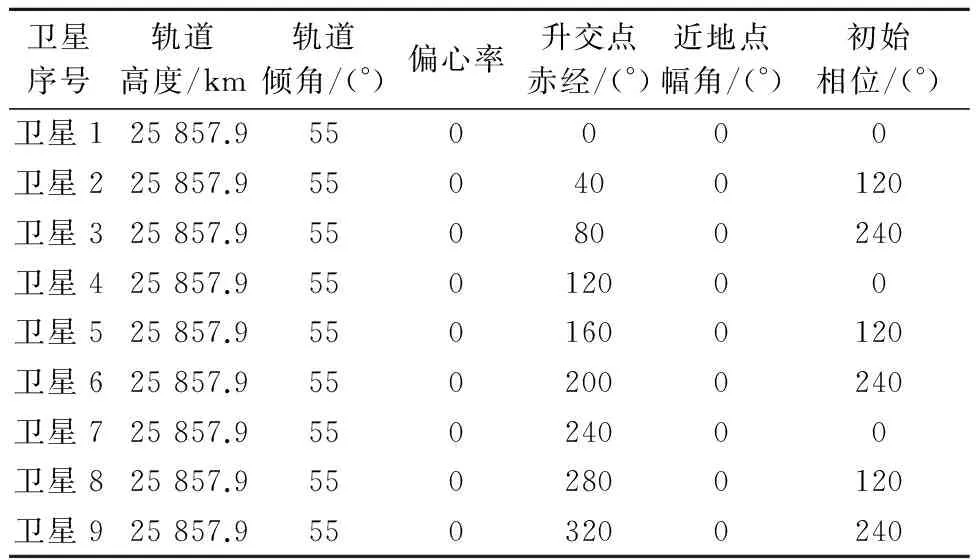
表1　构型为(9,2)的σ星座轨道参数

图2　构型为(9,2)的σ星座星下点轨迹图

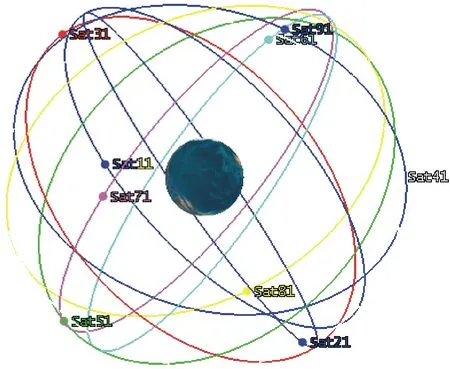
图3　构型为(9,2)的σ星座三维轨道构型

2.2N=9,D=3的σ星座

由于L=D+1，则回归圈数为L=4，利用式(9)可得

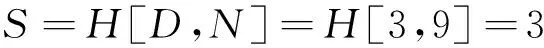
已知F为0～(P-1)之间的一个整数，代入验证以后，可得

也就是说，(9,3)构型的σ星座所对应的Walker星座构型为9/3/2，轨道参数如表2所示，图4和图5分别是该σ星座的星下点轨迹和三维空间轨道构型。

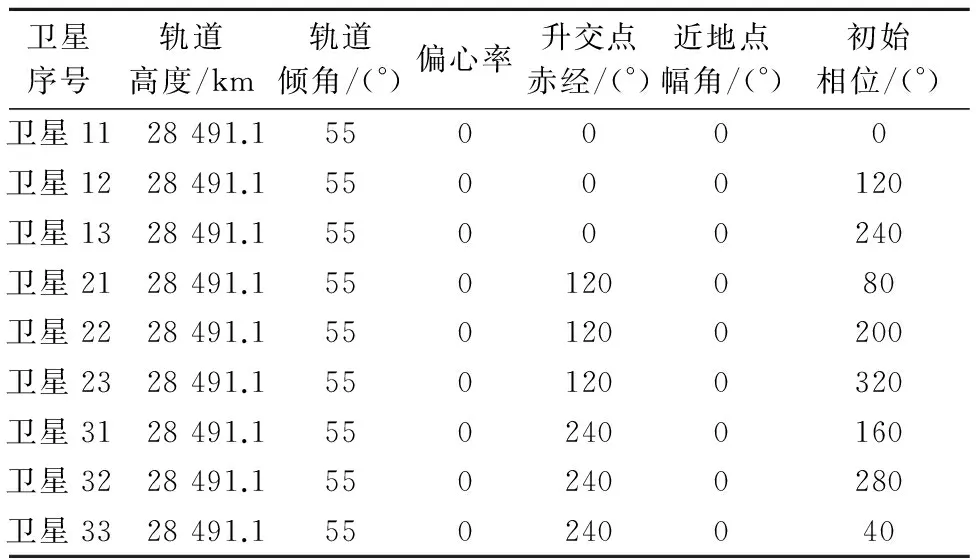
表2　构型为(9,3)的σ星座轨道参数

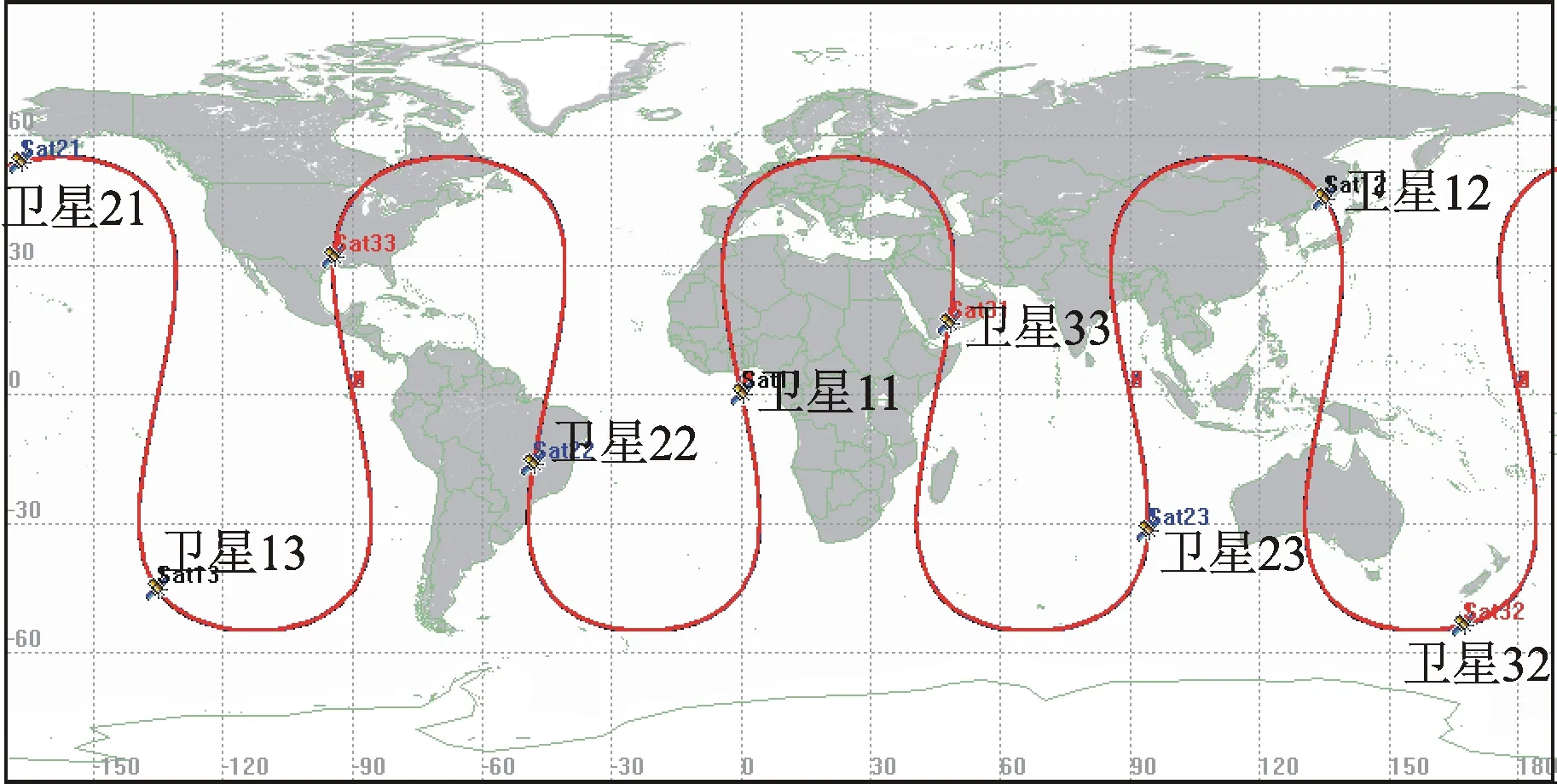
图4　构型为(9,3)的σ星座星下点轨迹图

图5　构型为(9,3)的σ星座星下点轨迹图

3　结 束 语

卫星星座的地面轨迹分离数越少，卫星星座对地面通信与测控站的需求数量就越少，这对于整个星座的测控和管理是非常有利的。然而，σ星座不仅星下点轨迹只有一条，而且整个星下点轨迹呈现出一条类似正弦曲线的特点，这使得σ星座构型比一般的地面轨迹分离数为1的回归轨道卫星星座构型更加简易，具有更大的工程应用价值。但是，通过仿真也可以看到，σ星座的轨道高度都比较高，属于高轨卫星星座。因此，可以将σ星座构型应用于通信卫星星座和预警卫星星座的设计，从而有效降低对轨道资源紧缺的地球静止轨道的依赖。

References)

[1]王永澄,付锋,尤鸣翔,等.中国区域卫星导航系统星座的方案探讨[J].南京航空航天大学学报,2003,35(5):480-484.

[2]项军华,张育林.区域覆盖星座构型优化及协同控制策略研究[J].飞行力学,2007,25(3):87-91.

[3]范丽.卫星星座一体化优化设计方法研究 [D].长沙：国防科技大学,2006：4-5.

[4]MAO Y,SUN F.Global navigation satellite constellation design using Walker constellation[J].Journal of Zhengzhou Institute of Surveying and Mapping,2006(2):18-20.

[5]WANG W,HUANG W D,FU X F,et al.Close approach of Walker constellation without orbital maneuver [J].Chinese Journal of Space Science,2005(6):55-59.

[6]BROCHET C,ENJALBERT J M,GARCIA J M.A multiobjective optimization approach for the design of Walker constellation[C]// 50th International Astronautical Congress.Amsterdam:IAF,1999：15-20.

[7]WALKER J G.Satellite constellations[J].Journal of the British Interplanetary Society,1984,37:559-572.

[8]KANTSIPER B,DRAKE H.Wave based design of satellite constellations[C]//Astrodynamics Specialist Conference.Denver：AIAA，2000:1-18.

[9]LONG F.Satellite network constellation design[M].Germany：Springer Berlin Heidelberg,2014:21-40.

[10]WALKER J G.Some circular orbit patterns providing continuous whole earth coverage[J].Journal of the British Interplanetary Society,1971,24:369-384.

[11]张雅声,樊鹏山,刘海洋，等.掌握与精通卫星工具箱STK[M].北京：国防工业出版社，2011:75-90.

(编辑：李江涛)

Simulation and Designing ofσConstellation

ZHANG Yasheng1,MO Wei2

(1. Department of Space Equipment, Equipment Academy, Beijing 101416, China;2. Beijing Spacecrafts, Beijing 100094, China)

σconstellation is a special type of Walker constellation with unique sub-star track. There is relative less description on design method ofσconstellation in literatures. Even if there are some illustrations, they are incomplete. Therefore, the paper studies on the relationship between ground track separation values andσconstellation configuration in depth, builds up spatial geometrical model ofσconstellation and proposes aσconstellation design and analysis method. Through STK software imitation, the paper verifies the feasibility of the design method. The imitation result shows, there is a huge perspective forσconstellation in the design of high-track communication satellite constellation and warning satellite constellation.

σconstellation; Walker constellation; constellation design; same ground track

2016-01-12

张雅声(1974—)，女，教授，博士，主要研究方向为飞行器设计与应用。13521219203@139.com

V412.41

2095-3828(2016)04-0049-04

A

10.3783/j.issn.2095-3828.2016.04.011