非标准条件对一维弹道修正弹弹道稳定性影响的研究
2016-09-20吴汉洲宋卫东徐敬青
吴汉洲,宋卫东,徐敬青
(1.军械工程学院 火炮工程系,河北 石家庄 050003;2.军械工程学院 弹药工程系,河北 石家庄 050003)
非标准条件对一维弹道修正弹弹道稳定性影响的研究
吴汉洲1,宋卫东1,徐敬青2
(1.军械工程学院 火炮工程系,河北 石家庄050003;2.军械工程学院 弹药工程系,河北 石家庄050003)
分析了阻力片打开前后弹丸弹道稳定性的变化规律,分析了弹道风、初始角速度扰动对一维弹道修正弹弹道稳定性的影响。以某型100 mm一维弹道修正弹为研究对象,建立了6自由度刚体弹道模型。仿真结果表明:弹道风、初始角速度扰动对一维弹道修正弹弹道稳定性的影响较小,在一般气象条件及初始扰动下,阻力片打开后弹丸可稳定飞行;阻力片打开会使弹丸攻角增大并伴随一定幅值的振荡,陀螺稳定性增强,动态稳定性先减弱后增强,追随稳定性减弱,落点侧偏有一定增加。
一维弹道修正;弹道风;初始角速度扰动; 弹道稳定性
随着科技的进步,精确制导武器在作战中使用频率不断升高,从海湾战争到伊拉克战争,战争中使用的精确制导弹药占总投弹量由8.36%提升到68%。弹道修正弹因只对常规弹药的引信加以改进,在改造成本不高的情况下却能使射击精度成倍提高,所以其一经提出便很快得到迅速发展[1-2]。
一维弹道修正弹在飞行中通过增加轴向空气阻尼进行射程上的修正,增加阻尼的方式主要是在弹头部弹出阻力片(环)。文献[3]从阻力环安装位置及展开面积入手,分析了阻力环对弹丸阻力系数、升力系数、俯仰力矩系数及压心系数的影响。文献[4]以一维弹道修正弹伞形阻力器为对象,在分析该阻力器对弹丸阻力系数等的影响基础上,通过数值模拟分析得出了阻力伞展开角度、修正时刻等因素与弹丸修正距离之间的规律。文献[5]以某型57 mm弹丸为研究对象,利用Fluent流体仿真软件,获得了弹丸在不同马赫数、阻力环不同展开高度、不同展开时刻及作用时间情况下的气动力参数,并通过外弹道程序验证了阻力环的增阻效果。以上文献总的结论为:弹丸飞行过程中,阻力片(环)对局部的流场有较大的影响,但产生的阻力系数随马赫数和攻角的变化规律没有改变;阻力片(环)打开后弹丸阻力系数增加明显,极阻尼力矩略有增加,升力系数有所减小,俯仰力矩系数减小,压心后移,有利于弹丸飞行稳定性[3,6]。
上述研究内容主要侧重于标准条件下通过风洞试验或计算流体力学软件分析阻力片(环)对弹丸飞行稳定性及对射程的修正量的影响等,而对非标准条件下弹丸飞行过程中阻力片(环)打时及打开后弹丸弹道稳定性的研究较少。
笔者以某型100 mm一维弹道修正弹为例通过弹道建模、仿真等分析了弹道风、初始角速度扰动等非标准条件下一维弹道修正弹弹道稳定性。
1 弹道建模及稳定性判据
1.1弹道微分方程组
运用Simulink软件建立了某型100 mm一维弹道修正弹刚体弹道模型。鉴于该弹为小射程近距离杀伤武器,模型忽略了地球表面曲率、弹丸质量偏心等对弹丸飞行的影响。依据文献[7]可建立相应弹道方程组。
1.2稳定性判据
1.2.1陀螺稳定性判据
(1)
式中:A、C分别为弹丸赤道转动惯量、极转动惯量;M为弹丸受到的静力矩;vr为弹丸相对速度。
当Sg≥1.3时弹丸具有陀螺稳定性。
1.2.2动态稳定性判据
仅满足陀螺稳定性判据的弹丸,在飞行中虽能稳定飞行,但其攻角可能会一直较大,特别当弹丸飞行中受到一定扰动出现攻角振荡时,弹丸攻角会一直振荡下去,而同时满足动态稳定性的弹丸,飞行中在攻角阻尼作用下,攻角会趋于减小,攻角振荡减弱。动态稳定因子为
(2)
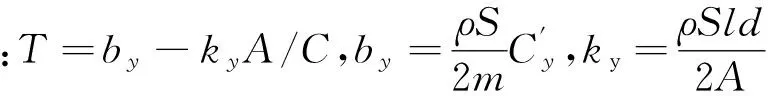
(3)
1.2.3追随稳定性判据
动力平衡角过大会影响弹丸射程,增大落点散布,甚至出现弹底着地,引信不起爆现象。动力平衡角最大值出现在最大射角射击时的弹道顶点附近,只要该值小于限制值δpm,则认为弹丸具有追随稳定性。对于右旋弹丸只考虑静力矩时的动力平衡角为
(4)
2 存在弹道风时阻力片打开对弹丸弹道稳定性的影响
弹道风主要包括弹道纵风(弹丸射击方向)和弹道横风(垂直于射击方向)。弹道风大小是随大气高度不断变化的,以我国某地区不同高度实测风速数据[7]为依据,在此基础上进行一定简化,假设弹道风大小随高度变化公式为
(5)
2.1弹道横风对阻力片不同打开时刻弹丸弹道稳定性影响
以某型100 mm一维弹道修正弹阻力片打开后产生原弹丸3.5倍阻力系数为仿真初始条件,在36°射角下设立如下仿真条件(无弹道纵风):
A0:无风条件下弹丸不打开阻力片。
A1:顺射击方向看横风风向由左向右,弹丸飞行10 s打开阻力片。
A2:顺射击方向看横风风向由左向右,弹丸飞行17 s打开阻力片。
A3:顺射击方向看横风风向由右向左,弹丸飞行10 s打开阻力片。
A4:顺射击方向看横风风向由右向左,弹丸飞行17 s打开阻力片。
其中弹丸飞行10 s左右一般为弹载计算机开始工作后能产生修正指令的最早时刻,弹丸飞行17 s时为弹道顶点。参考文献[3]的研究结论,在弹丸亚声速飞行条件下,设阻力片打开后弹丸升力系数、静力矩系数不变,压心位置后移约30%后不再随速度的变化而移动。
仿真结果表明,不同射角、阻力片不同时刻打开都会使弹丸陀螺稳定性增强,这也验证了文献[5]、[6]的结论,对此笔者不再列出仿真结果图。
图1、图2分别为存在弹道横风时阻力片不同打开时刻条件下弹丸攻角变化、动态稳定性判定值曲线图。表1为不同弹道横风及阻力片不同打开时刻下弹丸落点坐标。
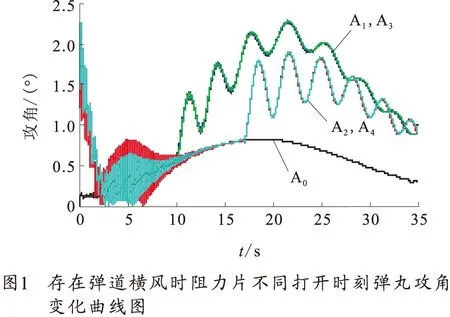

表1 存在弹道横风时弹丸落点坐标

仿真序列 x/mz/mA1 6461.0262.5A3 6449.145.7无风10s打开阻力片6459.7152.8A2 6989.8234.3A4 6979.549.0无风17s打开阻力片6989.6140.2
从图1中可看出,阻力片张开后弹丸攻角会不同程度的增大,且出现明显的振荡,但弹丸飞行一段时间后攻角减小,振荡幅值减小。图2为1/Sg+Sd2值随时间变化曲线,结合式(3)可知,阻力片在不同时刻打开时,由于阻力系数突然增加产生的扰动,使弹丸动态稳定性降低,但判定曲线会很快下降到无控弹动态稳定判定值以下,说明弹丸动态稳定性增强。这与图1中阻力片打开后弹丸攻角突然增加且振荡,一段时间后又开始减小并趋于稳定相对应。从图2中可看出,阻力片打开时间越早曲线瞬间跳变值越大,说明对弹丸动态稳定性影响越大。限于篇幅,没有列出弹丸过弹道顶点以后打开阻力片弹道特性变化。图1、图2中A1与A3、A2与A4曲线几乎重合,说明不同方向的弹道横风对弹丸飞行稳定性的影响相似。
从表1可看出,不同方向的弹道横风对弹丸引起的侧偏与无风条件下弹丸侧偏相差值较小,从射程上看,由左向右方向的弹道横风在一定程度上会增加弹丸射程,相反方向的弹道横风在一定程度上会减小弹丸射程。
2.2弹道横风对不同射角下打开阻力片后弹丸弹道稳定性影响
根据2.1节研究结论,只研究存在由左向右弹道横风,风速变化遵循式(5),无弹道纵风条件下,不同射角下阻力片打开弹丸飞行弹道稳定性。
仿真条件设分别在20°、28°、36°和44°射角下弹丸飞行弹道顶点处打开阻力片。阻力片张开后弹丸攻角、动态稳定性变化规律与2.1节中对一定弹道横风、阻力片不同时刻条件下对弹丸攻角、动态稳定性影响规律相似。
图3为存在弹道横风时不同射角下阻力片打开对弹丸追随稳定性判定值曲线图。
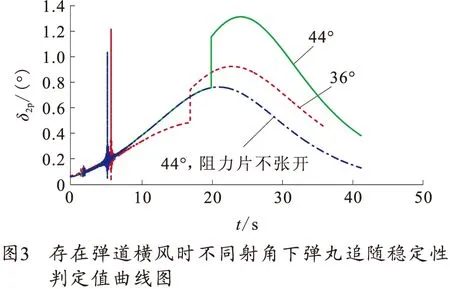
从图3中可看出,阻力片张开后弹丸追随稳定性下降,在射角为44°条件下打开阻力片后,δ2p最大值超过1.3°,弹丸失去追随稳定性(该型弹最大射角下δpm为0.951 6°)。该仿真条件下弹丸侧偏为319.2 m,阻力片不打开条件下侧偏为261.7 m,侧偏增大的原因有:前者仿真条件下弹丸飞行时间较后者多1.33 s;阻力片张开后一段时间里弹丸失去追随稳定性,但飞行一段时间后弹丸恢复追随稳定性。总体还可认为弹丸满足飞行稳定性,只是因阻力片打开增加了弹丸横向散布。
2.3弹道纵风对阻力片不同打开时刻弹丸弹道稳定性影响
设弹道纵风大小按照式(5)变化(无弹道横风),在36°射角下设立如表2仿真条件,仿真结果如图4和表3所示。

表2 不同弹道纵风下阻力片不同打开时间仿真条件设置表
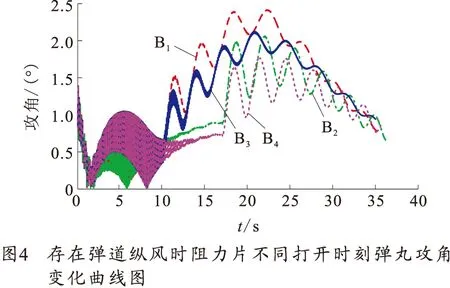
表3 存在纵风时弹丸落点坐标
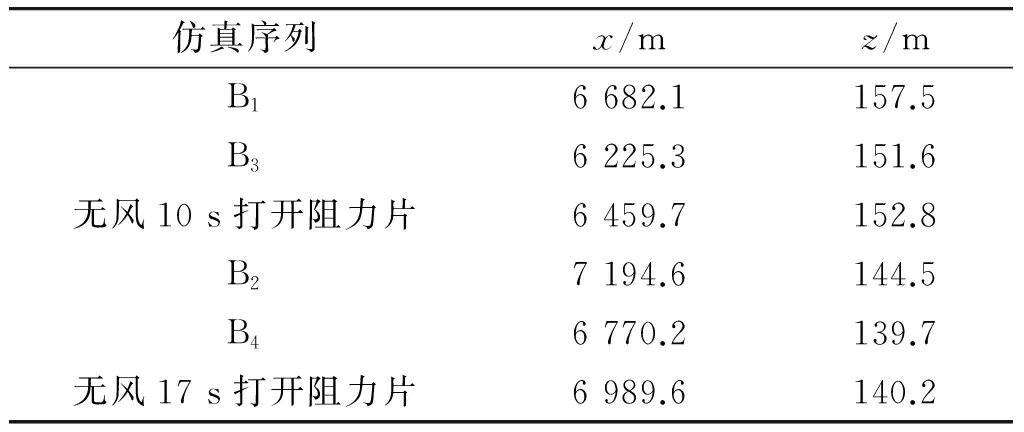
仿真序列x/mz/mB16682.1157.5B36225.3151.6无风10s打开阻力片6459.7152.8B27194.6144.5B46770.2139.7无风17s打开阻力片6989.6140.2
其中图4为存在弹道纵风时阻力片不同时刻打开阻力片弹丸攻角变化曲线,表3为相应弹丸落点坐标。
从图4中可看出,相同大小弹道纵风、相同时间打开阻力片条件下,弹道顺风环境下阻力片打开后对弹丸攻角的影响较弹道逆风大。在弹丸动稳定性判定值曲线图中B1、B3,B2、B4曲线几乎重合,说明相同大小、不同方向的弹道纵风环境下,阻力片打开后弹丸动稳定变化基本相同。从表3中可看出,阻力片在10 s打开时弹道顺风和弹道逆风引起的射程改变量分别为222.4 m、-234.4 m,阻力片在17 s打开时弹道顺风和弹道逆风引起的射程改变量分别为205 m、-219.4 m,说明相同大小弹道纵风条件下,弹道逆风引起的射程改变量较弹道顺风大。弹道纵风对弹丸侧偏较无风条件下影响较小。
2.4弹道纵风对不同射角下打开阻力片后弹丸弹道稳定性影响
根据2.3节研究结论,只研究存在弹道顺风,风速变化遵循式(5),无弹道横风时,不同射角下阻力片打开弹丸飞行弹道稳定性。
仿真条件设分别在20°、28°、36°、44°射角下弹丸飞行弹道顶点处打开阻力片。
仿真结果表明:阻力片张开后弹丸攻角、动态稳定性变化规律与2.3节中同一弹道纵风、不同时刻打开阻力片对弹丸攻角、动态稳定性影响规律相似,笔者不再列图说明。
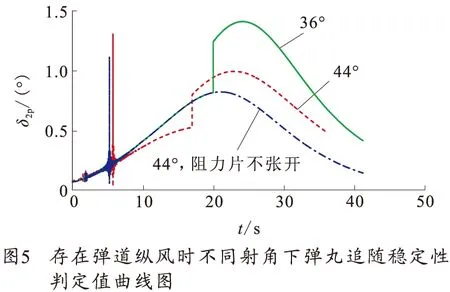
图5为不同射角下弹道纵风对弹丸追随稳定性判定值影响,从图5中可看出,阻力片张开后弹丸追随稳定性下降,在射角为44°条件下打开阻力片后, 最大值约为1.4°,弹丸失去追随稳定性。该仿真条件下弹丸侧偏为200.7 m,阻力片不打开条件下侧偏为178.1 m,侧偏增大的原因有:前者仿真条件下弹丸飞行时间较后者多1.31 s;阻力片张开后一段时间里弹丸失去追随稳定性,但飞行一段时间后弹丸恢复追随稳定性。总体还可认为弹丸满足飞行稳定性,只是因阻力片打开增加了弹丸横向散布。
3 初始角速度扰动对弹丸弹道稳定性的影响
初始角速度扰动主要包括Oη(位于铅垂面内,垂直于弹轴,向上为正)、Oζ(由右手螺旋定则确定)2个方向上的扰动,设2个方向上的初始角速度扰动分别为ωη0、ωζ0。在前期的研究中发现,2个方向上的初始角速度扰动对一维弹道修正弹弹道稳定性的影响相似,笔者以Oη方向上存在初始角速度为例,进行仿真说明。
3.1初始角速度扰动下阻力片不同打开时刻弹丸弹道稳定性研究
在36°射角下,设立如表4仿真初始条件,仿真结果如图6~8和表5所示,其中,图6~8分别为不同初始角速度扰动、阻力片不同打开时间下弹丸攻角曲线、动态稳定性判定值曲线和追随稳定性判定值曲线图,表5为不同仿真条件下弹丸落点侧偏数据。
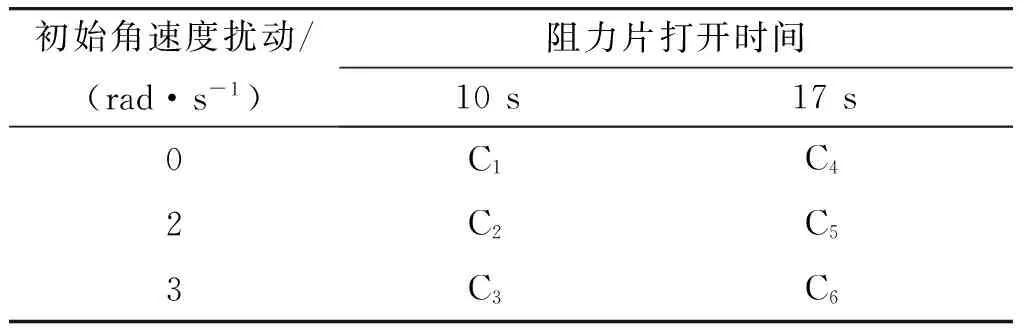
表4 不同角速度扰动时仿真条件设置
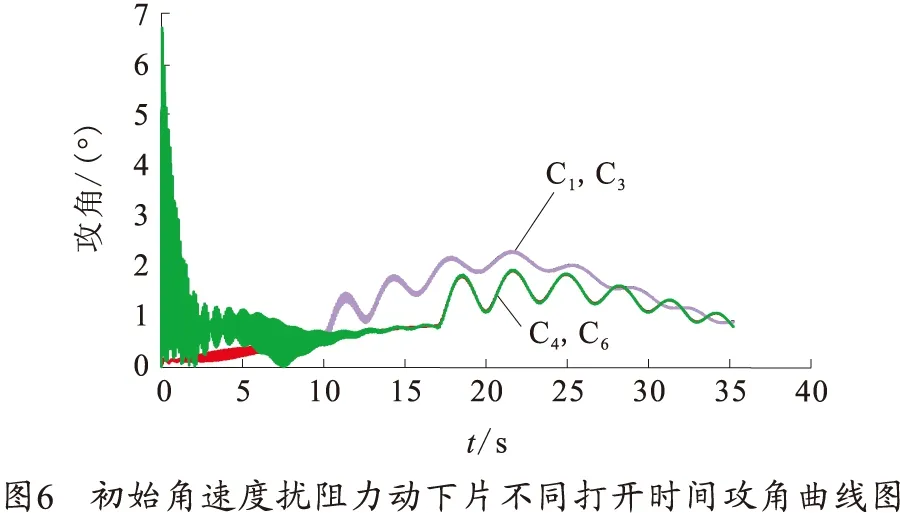
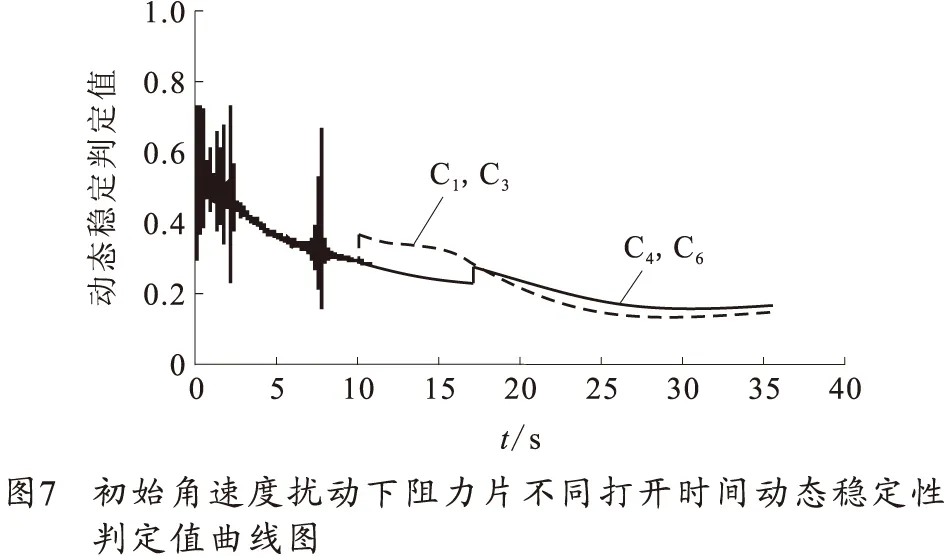
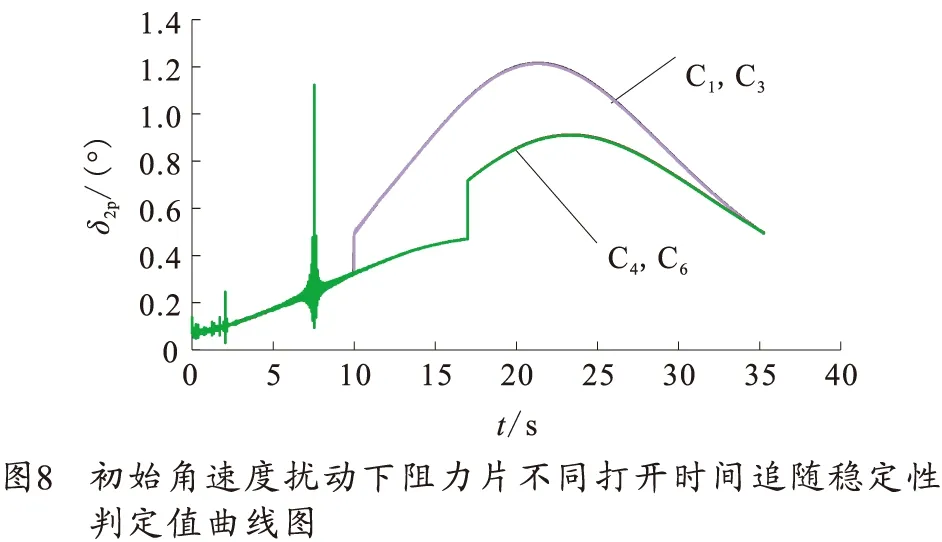
图6~8中,C1被C3曲线覆盖,C4被C6曲线覆盖。从图6中可看出,存在初始角速度扰动时,弹丸在出炮口后攻角会出现剧烈的振荡,从攻角变化趋势看,在弹丸出现攻角振荡期间阻力片打开对弹丸飞行攻角变化影响不大。从图7中可看出,初始角速度扰动总体对弹丸动态稳定性影响较小。从图8中可看出阻力片打开时间越早,追随稳定性判定值(动力平衡角)最大值越大,说明对弹丸追稳定性影响越大。从表5弹丸落点侧偏来看,阻力片打开对比不打开,弹丸落点侧偏明显增大,且打开时间越早引起的侧偏值越大,这与阻力片打开时间越早,对飞行追随稳定性影响越大相对应。

表5 弹丸落点侧偏表
3.2初始角速度扰动下射角取不同值时一维弹道修正弹弹道稳定性研究
从3.1节中可看出,在36°射角条件下,初始角速度扰动对弹丸弹道稳定性影响不大,为研究在其他射角下初始角速度扰动对一维弹道修正弹弹道稳定性的影响,笔者主要研究在20°、28°、44°射角条件下,初始角速度扰动ωη0=3 rad/s、阻力片在弹道顶点打开时对弹丸弹道稳定性的影响。图9~10分别为一定初始角速度扰动、不同射角下阻力片打开后弹丸攻角曲线图和追随稳定性判定值曲线图。
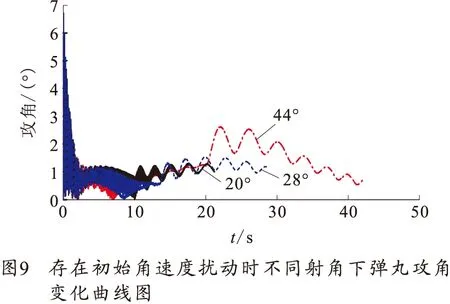
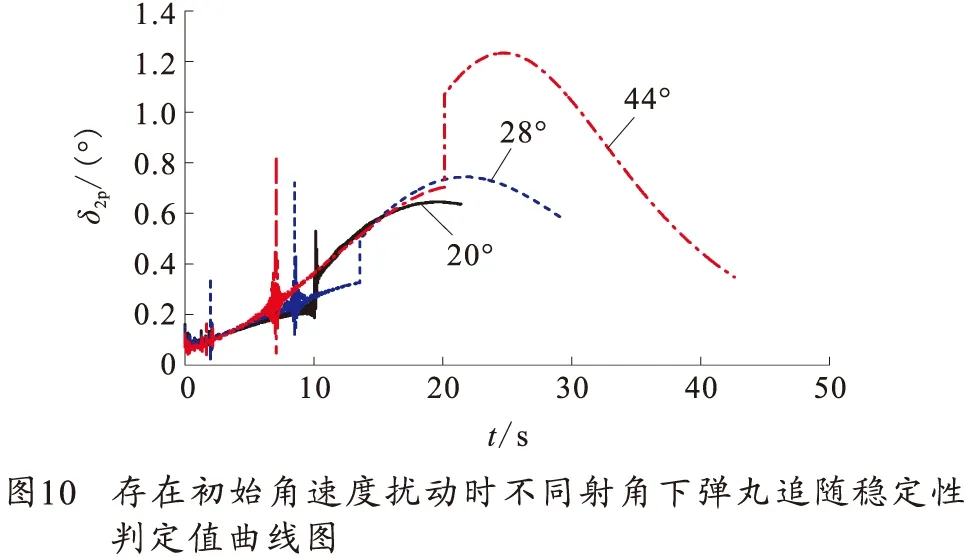
图9曲线变化规律与图6相似,说明初始角速度扰动对不同射角情况下弹丸飞行攻角影响规律相同,都使弹丸出炮口后产生较大的攻角幅值振荡,但对阻力片打开后攻角变化规律影响不大。不同射角下初始角速度扰动对弹丸陀螺稳定性和动态稳定性影响不大,较无扰动情况没有明显变化,本文不再列图说明。从图10中可看出在44°射角射击时若阻力片在弹顶甚至之前打开,则弹丸飞行将明显失去追随稳定性,飞行一段时间后将再恢复追随稳定性,这将使弹丸落点侧偏不同程度增大。
总体来说初始角速度扰动对一维弹道修正弹弹道稳定性的影响较小,在初始角速度扰动合理范围内,一维弹道修正弹阻力片打开对弹丸飞行稳定性影响不大,弹丸可继续稳定飞行。
4 结论
笔者以某型100 mm一维弹道修正弹为例,分析了弹道风、初始角速度扰动对一维弹道修正弹弹道稳定性的影响。仿真结果表明:弹道风的存在使弹丸出炮口后产生较大攻角,但攻角会很快减小;阻力片的张开会使弹丸攻角瞬间增大,并伴有一定幅值的振荡,一段时间后攻角及振荡幅值都会减小;阻力片的张开会使弹丸陀螺稳定性增强,动态稳定性先减弱后增强,追随稳定性减弱,且阻力片张开越早,追随稳定性减弱越明显,弹丸落点侧偏增大。初始角速度扰动会使弹丸出炮口后产生较大幅值的攻角振荡,阻力片打开后攻角增加,且仍伴随一定的幅值振荡。总体来说,弹道风、初始角速度扰动对一维弹道修正弹弹道稳定性的影响较小,在一般气象条件及初始角速度扰动下,阻力片打开后弹丸可照样保持一定的飞行稳定性。
References)
[1]陈科山,马宝华,何光林,等. 一维弹道修正引信阻力器的研究现状分析及其设计原则探讨[J]. 探测与控制学报, 2003, 25(3): 24-29.
CHEN Keshan,MA Baohua,HE Guanglin,et al.The study status and the design principle of damper of one dimension trajectory correction fuzes[J].Journal of Detection & Control, 2003, 25(3): 24-29. (in Chinese)
[2]张民权,刘东方,王东梅,等. 弹道修正弹发展综述[J]. 兵工学报, 2010, 31(2): 127-130.
ZHANG Minquan,LIU Dongfang,WANG Dongmei,et al.A summary for trajectory correction projectiles[J]. Acta Armamentarii, 2010,31(2):127-130.(in Chinese)
[3]裔萍. 一维弹道修正弹的气动力特性研究[D].南京:南京理工大学, 2006.
YI Ping.Study of one-dimension trajectory correction projectile aerodynamic characteristic[D]. Nanjing: Nanjing University of Science and Technology,2006.(in Chinese)
[4]吴雪飞. 一维弹道修正弹刚性伞形阻力器气动特性分析[D]. 太原:中北大学, 2013.
WU Xuefei. Aerodynamic characteristics analysis of rigid umbrella resistance device for one-dimensional trajectory correction projectile[D]. Taiyuan:North University of China, 2013. (in Chinese)
[5]徐永杰,吴国东,刘强,等.增阻式一维弹道修正弹气动分析[J].弹箭与制导学报, 2013, 33(6):133-136.
XU Yongjie,WU Guodong, LIU Qiang, et al. Aerodyna-mic analysis for damp-increasing one-dimensional trajectory correction shrapnel[J]. Journal of Projectiles, Roc-kets, Missiles and Guidance, 2013, 33(6):133-136.(in Chinese)
[6]于涛. 二维弹道修正弹的弹道特性研究[D]. 南京:南京理工大学, 2010.
YU Tao. A study on the ballistic characteristics of the two-dimension trajectory correction projectile[D]. Nanjing:Nanjing University of Science and Technology, 2010.(in Chinese)
[7]韩子鹏. 弹箭外弹道学[M].北京:北京理工大学出版社, 2008: 22, 260-271.
HAN Zipeng. Exterior ballistics of projectile and rocket[M]. Beijing:Beijing Institute of Technology Press,2008:22,260-271. (in Chinese)
[8]宋丕极. 枪炮与火箭外弹道学[M].北京:兵器工业出版社,1993:140-146.
SONG Piji. Exterior ballistics of gun and rocket[M]. Beijing:The Publishing House of Ordance Industry, 1993:140- 146.(in Chinese)
Study on Ballistic Stability of One Dimension Trajectory Correction Projectile in Non-standard Conditions
WU Hanzhou1,SONG Weidong1,XU Jingqing2
(1.Department of Artillery Engineering, Ordnance Engineering College, Shijiazhuang050003, Hebei, China;2.Department of Ammunition Engineering, Ordnance Engineering College, Shijiazhuang050003, Hebei, China)
An analysis is made of the ballistic stability around the time when the damper opened, and also of the influence of trajectory wind and initial angular velocity perturbation to the ballistic stability of one dimension ballistic correction projectiles. With a certain type of 100mm one dimension trajectory correction projectile as the research object, six DOF rigid body model was established. The simulation results show that the influence of trajectory wind and initial angular velocity on the ballistic stability of one dimension ballistic correction projectiles is slight. The projectile can have stable flight under the general meteorology conditions and initial angular velocity perturbation when the damper opened. The opening of the damper can increase the attack angle, accompanied with a measure of concussion. The gyro stability is enhanced, and the following stability weakened when the damper opened. First, the dynamic stability is at first weakened and then enhanced when the damper opened. The yaw is increased after the damper opened.
one dimension trajectory correction;trajectory wind;initial angular velocity perturbation;ballistic stability
10.19323/j.issn.1673-6524.2016.02.005
2015-07-02
吴汉洲(1989—),男,硕士研究生,主要从事弹箭弹道理论与应用技术研究。E-mail:18633049479@163.com
TJ012.3+1
A
1673-6524(2016)02-0019-06
