火炮武器-目标分配模型及其算法研究
2016-09-20耿修堂史国清石德乾
耿修堂,史国清,王 越,石德乾,何 浩
(西北机电工程研究所,陕西 咸阳 712099)
火炮武器-目标分配模型及其算法研究
耿修堂,史国清,王越,石德乾,何浩
(西北机电工程研究所,陕西 咸阳712099)
根据火炮不同作战任务或作战目的,防空反导火炮作战目标分配需遵循最大威胁法则,而远程压制火炮作战目标分配需遵循最大毁伤法则。针对火炮武器-目标分配问题,提出了两种典型的火炮武器-目标分配模型,分别为防空反导、远程压制目标分配。针对上述模型提出了基于模拟退火的目标分配优化算法,并通过嵌入局部领域贪婪搜索策略,提高了该算法的收敛速度和搜索效率。仿真结果表明,该算法具有收敛速度快、分配偏差低的优点,在军事领域具有潜在的应用价值。
火炮武器-目标分配;局部搜索;防空反导;远程压制
为了有效解决火力单元与毁伤目标的合理匹配,火炮武器-目标分配NP优化问题被提出。目标分配是火力打击作战指挥决策过程中的重要内容,是信息化条件下协同作战中的一项重要任务。
目标分配问题一直是军事研究领域的热点问题,求解目标分配常用方法包括全局搜索算法、动态规划算法、匈牙利算法[1]和软计算方法等。近年来各种软计算方法被频繁地用于求解火力分配问题,如遗传算法[2-5]、混合跳蛙算法[3]、捕食搜索算法[4]、蚁群算法[5-7]、人工免疫算法[8]和粒子群优化算法[9]等。同时,各种算法混合应用以提高搜索效率被不断尝试。例如,在文献[3]中遗传算法和跳蛙算法被混合用于求解火力分配问题;文献[4]中遗传算法和捕食搜索算法被混合用于求解火力分配问题;文献[5]中遗传算法和蚁群算法被混合用于求解火力分配问题,仿真结果表明能在一定程度上弥补单个算法存在收敛速度或精确度的缺陷。
通过描述火炮武器-目标分配模型,分别建立基于最大威胁法则的防空火炮-目标分配模型及基于最大毁伤法则的压制火炮-目标分配模型。运用一种简单的模拟退火算法[10]并进行改进,开展火炮武器-目标分配研究,尝试用更短时间得到更低分配偏差率,为火炮武器实时火力分配提供参考。
1 火炮武器-目标分配数学模型
笔者主要结合防空反导、远程压制两类典型火炮的作战任务或目的,分别进行对应的火炮武器-目标分配数学建模。
1.1防空反导火炮武器-目标分配模型
假设在有效的作用区域和时间内,防空反导编队共有W门防空高炮,T个来袭敌目标,某门防空高炮只能分配给某个来袭目标。假定所有的防空高炮必须分配给来袭目标,分配时刻每门防空高炮对来袭目标的毁伤概率已知,每个来袭目标的威胁度已知。
防空反导火炮防御作战时,其任务主要是保护军事要地,故基于最大威胁法则的防空反导火炮武器-目标分配的数学模型为
(1)
式中:X为初始解或决策矩阵;xij为第i门防空高炮对第j个来袭目标的分配结果,xij=0表示未分配,xij= 1表示分配;kij为第i门防空高炮对第j个来袭目标的毁伤概率;wj表示第j个来袭目标的威胁度。
1.2远程压制火炮武器-目标分配模型
同样地,假设在有效的作用区域和时间内,远程压制编队共有W门压制地炮,T个地面目标,某门压制地炮只能分配给某个地面目标。假定所有的压制地炮必须分配给前方地面目标,分配时刻每门压制地炮对地面目标的毁伤概率已知,每个地面目标的威胁度已知。
压制火炮远程压制作战时,其任务主要是摧毁前方的地面目标,故基于最大毁伤法则的远程压制火炮-目标分配的数学模型为
(2)
类同防空反导模型中的参数定义,X为初始解或决策矩阵;xij为第i门压制地炮对第j个地面目标的分配结果,xij=0表示未分配,xij=1表示分配;kij为第i门压制地炮对第j个地面目标的毁伤概率;cj表示第j个地面目标的价值度。
2 火炮武器-目标分配优化算法
2.1模拟退火算法
20世纪80年代,模拟退火思想被成功地引入到组合优化领域。特别是进入21世纪,伴随着计算机技术发展和计算机的普及,模拟退火算法在工程中得到了广泛应用。
模拟退火算法来源于固体退火原理,是一种基于概率的算法,将固体加温至充分高,再让其逐渐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而逐渐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
模拟退火算法实现时,是从某一较高初温出发,伴随温度参数不断下降,结合概率突跳特性在可行解空间中随机寻找目标函数的全局最优解,即局部最优解理论上存在概率性地跳出并最终趋于全局最优的可能。
2.2领域搜索策略
如图1所示,其中矩阵X[i][j]为初始解,矩阵中元素xij=1表示第i武器分配第j目标,xij=0表示第i武器没有分配第j目标,这里i=7表示武器数量为7,j=15表示目标数量为15。
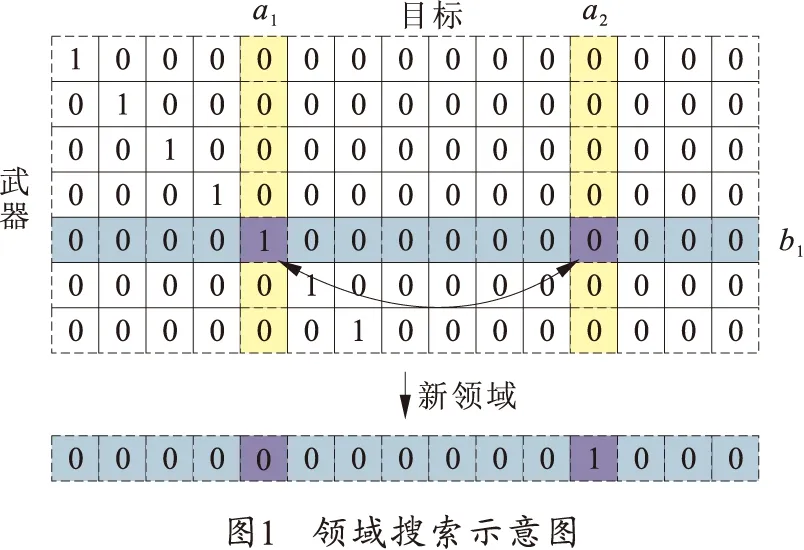
图1中基于某个初始解,领域搜索策略首先随机选择第b1武器,再把该武器已分配目标a1变换为新的目标a2,这里a1≠a2。这样,原来的领域状态为xb1a1=1、xb1a2=0,领域搜索后,新的领域状态为xb1a1=0、xb1a2=1。
2.3算法流程
目标分配优化算法流程如图2所示。
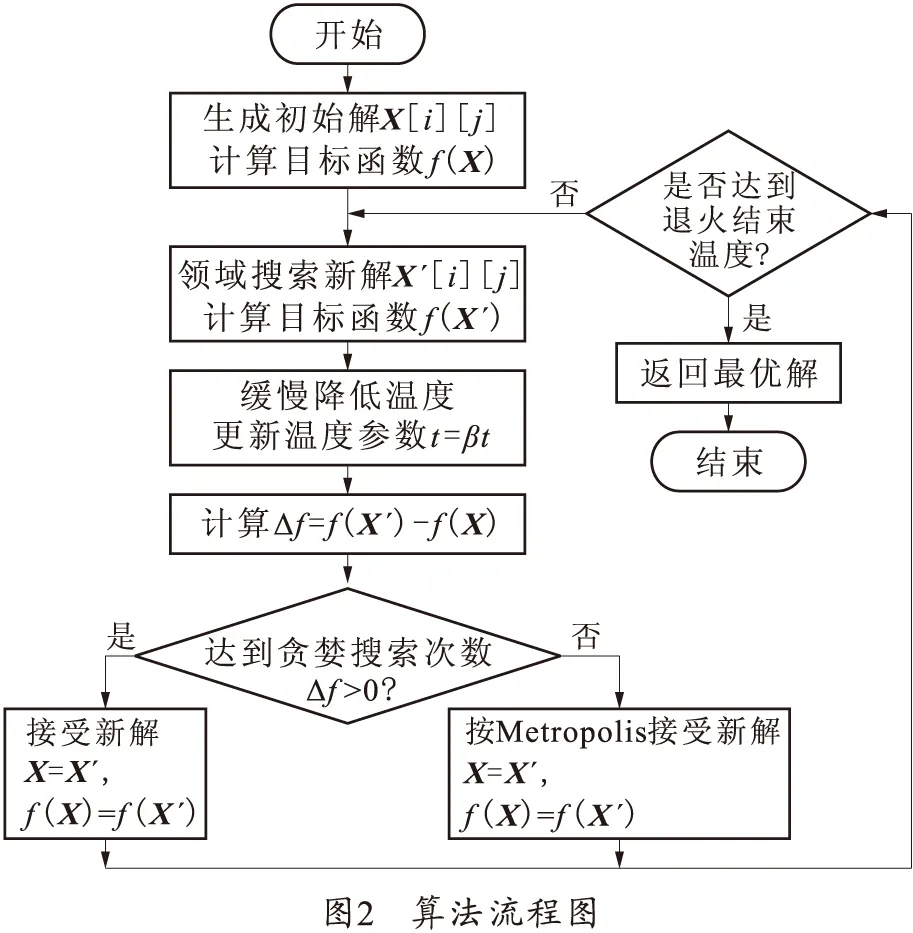
新解的产生和接受主要分为如下几个步骤:
1)按照各武器分配至当前威胁最大目标的要
求,生成初始解X[i][j],防空反导火炮武器-目标分配按式(1)计算目标函数,远程压制火炮武器-目标分配按式(2)计算目标函数。
2)按照图1所示的领域搜索策略,随机生成新解X′[i][j],按式(1)或(2)计算新目标函数。
3)缓慢降低退火温度,计算目标函数值增量Δf=f(X′)-f(X)。
4)如果Δf>0或达到贪婪搜索次数,接受新解,X=X′且f(X)=f(X′);否则,按Metropolis接受新解。
5)如果已达到退火结束温度,返回最优解,算法结束;否则,重复步骤2至步骤5。
3 仿真分析
3.1案例假定
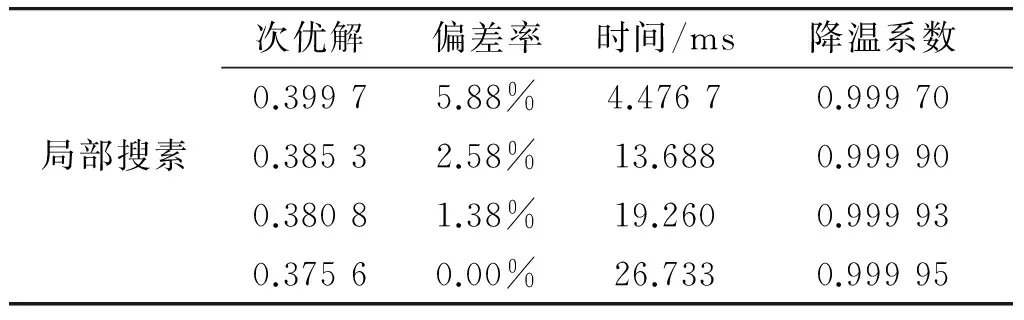
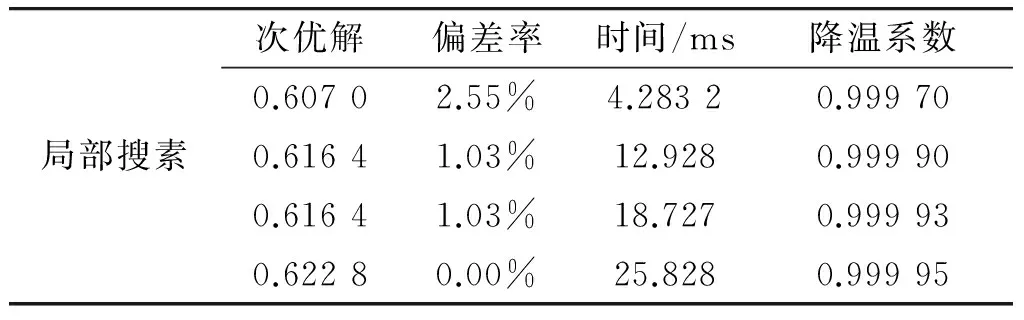
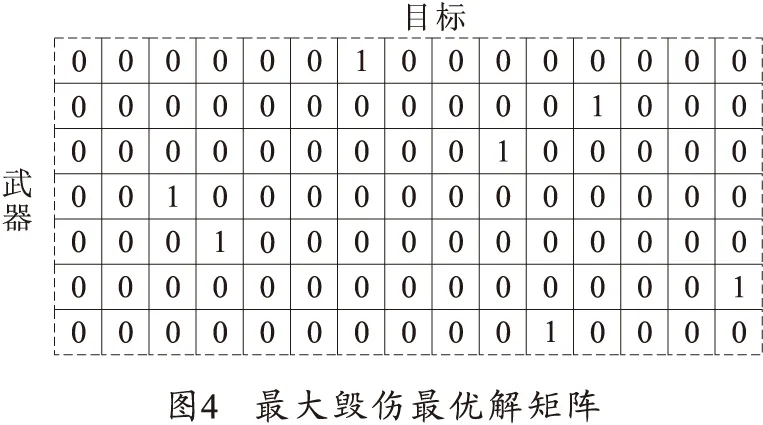
假设火炮武器的数量为i=7,来袭目标的数量为j=15。武器对目标毁伤概率、目标威胁度权重及目标价值度权重如表1所示。表1中前7行矩阵表示7个武器对15个目标的毁伤概率kij,且0 表1 武器对目标毁伤概率、目标威胁度权重及目标价值度权重 3.2最大威胁法则仿真结果 基于表1案例的最大威胁法则及对应模型的全局搜索计算结果如表2所示。 表2 最大威胁法则全局搜索仿真结果 基于表1案例的防空反导火炮武器-目标分配的最大威胁法则及对应模型的仿真计算和结果如表3所示。其中偏差率=(次优解-最优解)/最优解×100%。 表3 最大威胁法则局部搜索仿真结果 如表2、3所示,当采用全局搜索求解最优解需耗时53 916 ms;而采用本文算法求解最优解只需26.733 ms,偏差率为0.0%;求解次优解分别需耗时19.260、13.688和4.4767 ms(偏差率分别为1.38%、2.58%和5.88%)。对应的最优解矩阵如图3所示。 3.3最大毁伤法则仿真结果 基于表1案例的最大毁伤法则及对应模型的全局搜索计算结果如表4所示。 表4 最大毁伤法则全局搜索仿真结果 基于表1案例的远程压制火炮武器-目标分配的基于最大毁伤法则及对应模型的仿真计算和结果如表5所示。其中偏差率=(最优解-次优解)/最优解×100%。 表5 最大毁伤法则局部搜索仿真结果 如表4、5所示,当采用全局搜索求解最优解需耗时57 541 ms;而采用本文算法求解最优解需时25.828 ms,偏差率为0.0%;求解次优解分别需18.727、12.928和4.283 2 ms(偏差率分别为1.03%、1.03%和2.55%)。对应的最优解矩阵如图4所示。 现代战争越来越重视火控协同和系统作战,武器系统越来越复杂,指挥决策的时效性越来越重要。在此背景之下,目标分配面临速度和精度双重挑战。传统的全局搜索算法在有限的时间内已不能求解目标分配问题,而各种启发式算法能在有限的时间内求解出能够接受的次优解,在军事信息处理领域具有潜在的应用价值,提出的火炮武器-目标分配模型及改进模拟退火启发式优化算法,仅仅从基础理论角度进行初步的分析和验证,毁伤概率、威胁度、价值度等都是随机生成的,旨在验证算法的有效性。而要实现火炮武器-目标分配工程化应用需要对目标特性、分配模型进行更深入的研究和适应性改进,特别是威胁度、毁伤度建模,并建立对应的特性专家库,这是下一步工作研究重点。 References) [1]彭琛, 李建立, 王琦. 基于改进匈牙利算法的自组网火力分配[J]. 弹箭与制导学报, 2014, 34(5): 169-172,179. PENG Chen, LI Jianli, WANG Qi. Firepower assignment by improved Hungarian algorithm based on ad hoc networks[J]. Journal of Projectiles, Rockets, Missiles and Gui-dance, 2014, 34(5): 169-172,179. (in Chinese) [2]LEE Znejung, SU Shunfeng, LEE Chouyuan. Efficiently solving general weapon-target assignment problem by genetic algorithms with greedy eugenics[J]. IEEE Transactions on Systems, Man, and Cybernetics,Part B: Cybernetics, 2003, 33(1): 113-121. [3]阮旻智, 李庆民, 刘天华. 编队防空火力分配建模及其优化方法研究[J]. 兵工学报, 2010, 31(11):1525- 1529. RUAN Minzhi, LI Qingmin, LIU Tianhua. Modeling and optimization on fleet antiaircraft firepower allocation[J]. Acta Armamentarii, 2010, 31(11): 1525-1529. (in Chinese) [4]汲万峰, 王光源, 章尧卿, 等. 基于PSGA的岸基导弹火力分配研究[J]. 现代防御技术, 2014, 42(2): 77-83, 94. JI Wanfeng, WANG Guangyuan, ZHANG Yaoqing, et al. Fire distribution for shore-based missiles based on PSGA[J]. Modern Defence Technology, 2014, 42(2): 77-83, 94. (in Chinese) [5]陈云飞, 刘玉树, 范洁, 等. 火力优化分配问题的小生境遗传蚂蚁算法[J]. 计算机应用, 2005, 25(1): 206- 209. CHEN Yunfei, LIU Yushu, FAN Jie, et al. Niche-based genetic & ant colony optimization algorithm for generalized assignment problem[J]. Computer Applications, 2005, 25(1): 206-209. (in Chinese) [6]LEE Znejung, SU Shunfeng, LEE Chouyuan. An immunity-based ant colony optimization algorithm for solving weapon-target assignment problem[J]. Applied Soft Computing, 2002(2): 39-47. [7]郭蕴华, 李运涛, 杨福缘. 考虑毁伤概率门限的火力分配变异蚁群算法[J]. 火炮发射与控制学报, 2006(4): 1-5,11. GUO Yunhua, LI Yuntao, YANG Fuyuan. Mutation ant colony algorithm for weapon target assignment problem based on threshold of damage probability[J]. Journal of Gun Launch & Control, 2006(4): 1-5,11. (in Chinese) [8]张凯, 周德云, 潘潜. 基于混合蛙跳算法的协同空战火力分配[J]. 计算机工程与应用, 2014, 50(17):263- 266. ZHANG Kai, ZHOU Deyun, PAN Qian. Weapon-target assignment based on shuffled frog leaping algorithm in cooperative air combat[J]. Computer Engineering and Applications, 2014, 50(17): 263-266. (in Chinese) [9]王光源, 徐鹏飞, 赵勇. 基于粒子群优化算法求解火力分配问题[J]. 舰船电子工程, 2013, 33(11):34- 36. WANG Guangyuan, XU Pengfei, ZHAO Yong. A solution of weapon-target assignment problems based on particle swarm optimization[J]. Ship Electronic Engineering, 2013, 33(11): 34-36.(in Chinese) [10]GENG Xiutang, XU Jin, XIAO Jianhua, et al. A simple simulated annealing algorithm for the maximum clique problem[J]. Information Sciences, 2007, 177(22): 5064-5071. Research on Model and Algorithm for Artillery Weapon-target Assignment GENG Xiutang, SHI Guoqing, WANG Yue, SHI Deqian, HE Hao (Northwest Institute of Mechanical & Electrical Engineering, Xianyang712099, Shaanxi, China) According to the different operational tasks and purposes of artillery, weapon-target assignment for air defense and anti-missile artillery needs to follow maximum threat principles, while weapon-target assignment for remote attacking artillery needs to follow maximum damage principles. With regard to the artillery weapon-target assignment problem, two models for air defense and anti-missile and remote attacking are proposed. The weapon-target assignment optimization algorithm based on simulated annealing is presented, and the convergence rate and searching efficiency for the algorithm are enhanced by means of embedding greedy search strategy in local area. Computational results indicate that the proposed algorithm has the advantage of fast convergence rate and low allocation deviation, and can find potential application value in military field. artillery weapon-target assignment; local search; air defense and antimissile; long range neutralization 10.19323/j.issn.1673-6524.2016.02.009 2015-10-19 兵器支撑预研项目(62201020101) 耿修堂(1975—),男,博士,高级工程师,主要从事火炮信息与控制技术研究。E-mail:gxt1028@163.com TJ301 A 1673-6524(2016)02-0041-05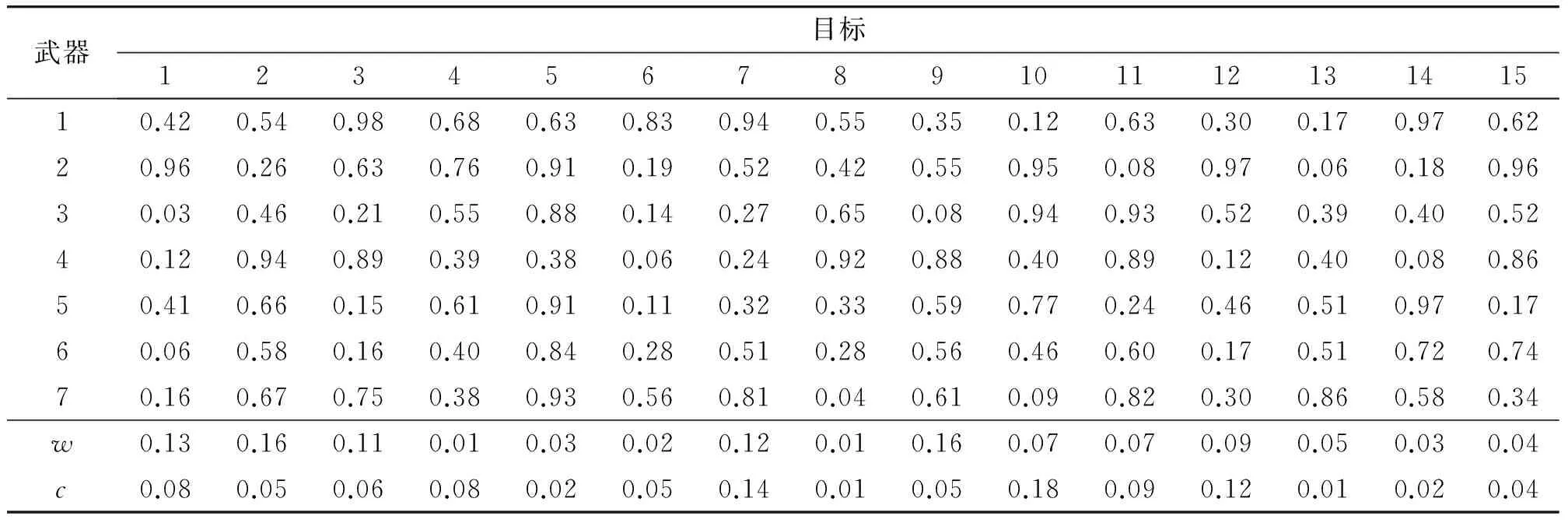



4 结束语
