约束圆环试验混凝土裂缝扩展全过程研究

罗　昊，荣　华，袁文岩，董　伟

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.中冶建筑研究总院， 北京 100000)



约束圆环试验混凝土裂缝扩展全过程研究

罗昊1，荣华2，袁文岩1，董伟1

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.中冶建筑研究总院， 北京 100000)

美国国家公路与运输协会(AASHTO)及美国试验材料学会(ASTM)推荐约束圆环试验为评估早期混凝土抗裂性的标准试验方法。为了更好地研究约束圆环试验中混凝土的破坏机理，利用ANSYS有限元软件热学分析和结构分析模块，在混凝土上施加虚拟温度场来模拟收缩作用。结合应力分析结果确定混凝土的起裂位置，并引入虚拟裂缝模型，模拟外圆周干燥的圆环试件收缩裂缝在起裂后的扩展过程。通过对比混凝土开裂时间，预测结果和试验结果吻合良好，验证了数值模拟中提出的计算方法的可行性。结果显示，在约束圆环试验中，限制收缩裂缝形成后直接进入失稳扩展阶段，试验中钢环压应变的突然滞回反映了混凝土限制收缩条件下的失稳扩展。

约束收缩；破坏机理；虚拟裂缝模型；裂缝扩展

内部湿度变化及自身的水化反应会引起混凝土的收缩，进而产生体积变化，这在早龄期混凝土中体现更为显著。当这种体积改变受到外部的约束，会在混凝土内部产生拉应力，由于早期混凝土抗拉强度较低，一旦产生的拉应力大于其抗拉强度，混凝土就会开裂。这种收缩裂缝在一些大表体比(A/V)结构中尤其显著，例如高速公路，桥面板，工业地坪等。这是混凝土的主要病害之一。因此如何有效地评估早龄期混凝土的开裂性一直是工程界和学术界关注的问题。约束圆环试验可获得足够的均匀约束，且便于挪动，又可以在实验室条件下进行操作，被美国国家公路与运输协会(AASHTO)[1]及美国试验材料学会(ASTM)[2]推荐为评估早龄期混凝土抗裂性的标准试验方法。约束圆环试验在我国已经广泛应用于高强混凝土[3]、自密实混凝土[4]、轻骨料混凝土[5]和微粉混凝土[6]等抗裂性测试中。目前对于限制收缩破坏的机理分析可以归纳为传统强度理论方法[7-9]和断裂理论方法[10-12]。传统强度理论认为，混凝土在约束收缩条件下，当内部形成的最大周向应力大于其抗拉强度时，则视为裂缝出现，考虑到收缩徐变产生的应力松弛，在强度理论中实际起控制作用的为残余应力[7-9]。但一些学者[10-12]也指出，由于混凝土的抗拉强度存在着尺寸效应，而且混凝土在限制收缩状态下呈现拉压复合应力状态，此时再单纯采用混凝土单轴抗拉强度来进行判断裂缝出现是不准确的，所以一些学者提出基于断裂力学的R阻力曲线方法[13-14]分析混凝土中裂缝的出现，尽管R阻力曲线将试件尺寸对裂缝出现的影响考虑其中，却也停留在判断混凝土破坏的阶段，无法描述裂缝的整个扩展过程。同时ASTM推荐的试验方法中应变滞回仅仅代表内部约束作用的释放，对于混凝土起裂和失稳在标准中没有明确指出。

基于上述原因，本文拟通过施加于混凝土的虚拟温度场模拟收缩作用，研究混凝土限制收缩裂缝的产生及扩展过程。采用ANSYS软件热学分析和结构分析模块，通过弹性理论分析获取混凝土内部的周向应力分布，当其超过劈拉强度时混凝土出现开裂。在此基础上建立虚拟裂缝模型，基于非线性断裂理论，引入裂缝扩展准则来研究混凝土起裂后裂缝扩展的全过程，并分析得到混凝土圆环的应力强度因子(记为SIF)随着龄期增长的变化规律，研究圆环试验中混凝土在限制收缩条件下的破坏机理。

1　试验分析

采用配合比为水泥∶沙子∶石子∶水=1∶1.5∶1.5∶0.5的混凝土，同时试验中所有试件在温度23℃、相对湿度50%的环境中养护。

1.1材料性能试验

参照《普通混凝土力学性能试验方法标准》[15](GBT 50081-2002)，劈拉试验试件采用150 mm×150 mm×150 mm的立方体；弹性模量试验试件取150 mm×150 mm×300 mm的棱柱体；三点弯曲梁采用100 mm×100 mm×500 mm的标准试件，初始缝高比a0/D设定为0.33。选取1 d、3 d、5 d、7 d、14 d、21 d和28 d龄期点试件，分别按照标准试验方法进行试验。对上述试验结果进行拟合回归，得到断裂能、劈拉强度和弹性模量随龄期变化的函数，分别如式(1)、式(2)和式(3)所示，其中t表示龄期，d，断裂能Gf的单位为N/m，劈拉强度fst的单位为MPa，弹性模量Ec的单位为GPa。

Gf(t)=41.913+10.350×ln(t-0.326)

(1)

fst(t)=1.244+0.44×ln(t-0.0318)

(2)

Ec(t)=13.8973+0.4000t-0.0056t2

(3)

1.2自由收缩试验

参照标准[16]，为了测量表体比对早龄期混凝土自由收缩量的影响，试验中混凝土棱柱体采用四种不同的封闭方式，具体为侧面全封闭，侧面无封闭，三侧面封闭和两侧面封闭，并且四个试件的上下面全部封闭。此时四个试件的表体比为0，0.0533/mm，0.0133/mm和0.0267/mm，为了保证封闭质量，试验中用两层带胶锡带纸封闭试件。试验中收缩量采用精度为0.001 mm的千分表进行测量，每天9∶00和21∶00两个时间记录变形量，观测28 d。

1.3约束圆环试验

参考ASHHTO[1]和ASTM[2]两个标准，试验中，收缩试件的钢环厚度为12.5 mm，混凝土壁厚37.5 mm，钢环外径为150 mm，在混凝土从外圆周表面干燥的情况下，研究限制收缩下混凝土的裂缝的产生与扩展等特性。试验中，通过观察粘贴于钢环内侧的应变计的示数变化确定混凝土的开裂时间，同时定期观测混凝土周向外表面确定裂缝起裂位置。图1给出圆环试验中钢环压应变的示数变化，钢环压应变突然滞回所对应的时刻即为混凝土开裂的时间，因此可以判断出圆环分别在第15 d、第16 d和第14 d开裂。

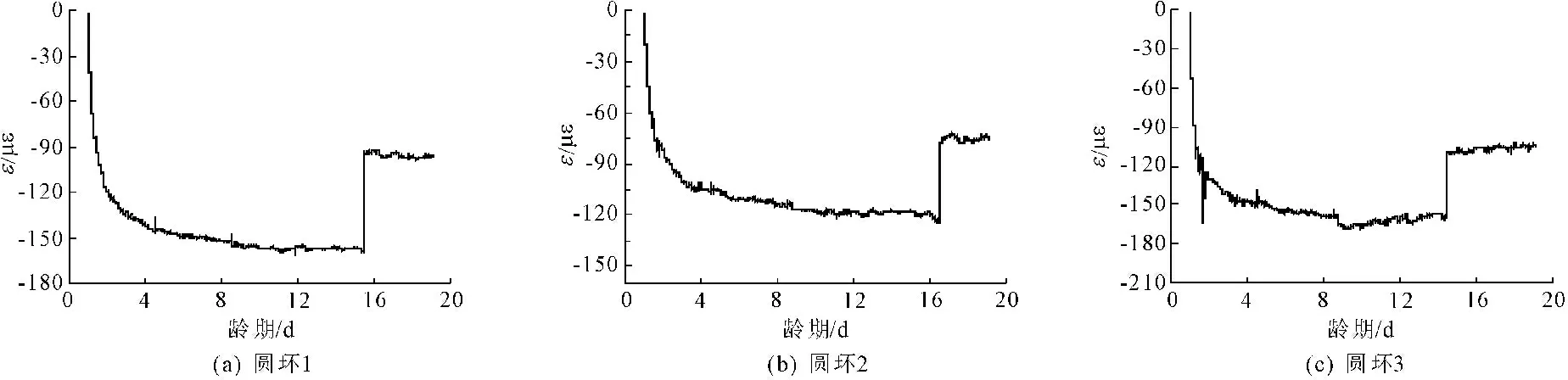
图1约束钢环压应变

2　数值模拟

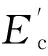
2.1热学分析

考虑到虚拟温度场下混凝土圆环产生的变形与自由收缩条件下的变形相同。因此引入温度变形公式Δl=α·l·Δt，其中α表示热膨胀系数，Δt表示温度变化，Δl和l分别表示变形量和原长度。在常用混凝土热膨胀系数α为10-6/℃情形下，可以反推获得上述四种体表比的混凝土随龄期的虚拟温度曲线。但是在实际的数值模拟中，混凝土构件拥有不同的几何形式和尺寸，此时暴露于空气中的面积和构件的体积都发生了变化，表现为具有与上述试验不同的表体比，所以需要通过线性插入的方式获得应用于实际构件的虚拟温度曲线。本文中开展混凝土圆环试件的数值模拟，钢环外径Ros=150 mm，混凝土壁厚37.5 mm，表体比为0.0296/mm，图2给出不同体表比的虚拟温度曲线。图3给出数值计算中龄期为14 d时混凝土上的虚拟温度场，混凝土上有着-25.56℃的虚拟温度场，分析的基准温度为0℃。

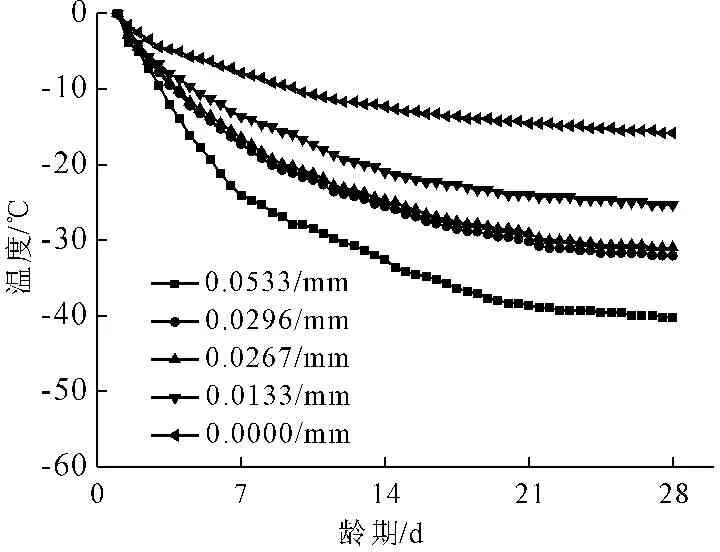
图2　不同体表比棱柱体的虚拟温度曲线

图3虚拟温度场

2.2结构分析

虚拟温度场的施加，会使混凝土产生收缩，在内部钢环约束作用下内部会产生拉应力，当最大拉应力超过抗拉强度时产生裂缝。数值计算结果显示，圆环试验中裂缝随机产生于混凝土环内侧，如图4所示。在混凝土起裂后，在最大环向拉应力处设置2 mm的预制裂缝。为了考虑宏观裂缝前端微裂区的材料软化，本文采用Hillerborg[18]提出的虚拟裂缝模型，对裂缝两侧施加黏聚力，模拟限制收缩作用下混凝土裂缝扩展全过程，图5给出虚拟裂缝模型中裂缝尖端的处理方式。混凝土拉伸软化本构模型采用Peterson[19]提出的双线性σ-w软化模型，转折点的位移和应力的确定如式(4)，其中w0表示黏聚力为零时的裂缝张开口位移，ws和σs分别为软化曲线转折点的裂缝张开口位移和黏聚力，ft和Gf分别表示混凝土的抗拉极限强度和断裂能。

图4　环向应力场

图5裂缝尖端处理

σs=ft/3

ws=0.8Gf/ft

(4)

w0=3.6Gf/ft

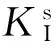
(1) 确定混凝土的材料性能：劈拉强度ft、弹性模量E、断裂能Gf；

(2) 确定圆环试件随龄期的虚拟温度下降曲线，即虚拟温度场；

(3) 施加不同龄期的虚拟温度场，开展混凝土弹性分析，当混凝土内产生的拉应力大于抗拉强度时，判断混凝土裂缝产生位置。基于虚拟裂缝模型，建立数值计算模型，在裂缝处预制初始长度a0=2mm的裂缝；

(5) 给定的裂缝增量Δa=2mm，重复步骤(4)和(5)直到裂缝贯穿整个混凝土环壁厚，停止计算。

3　结果分析与讨论

混凝土在虚拟温度场作用下产生了收缩，而在内部钢环约束作用下，使混凝土内部产生拉应力，图3给出了14 d龄期的约束圆环试件混凝土内部的环向应力场，从中可以看出混凝土圆环试件最大拉应力为2.39 MPa，而从式(2)中可知道抗拉强度为2.38 MPa，说明混凝土在14 d开裂，开裂时间与约束圆环试验结果吻合良好。

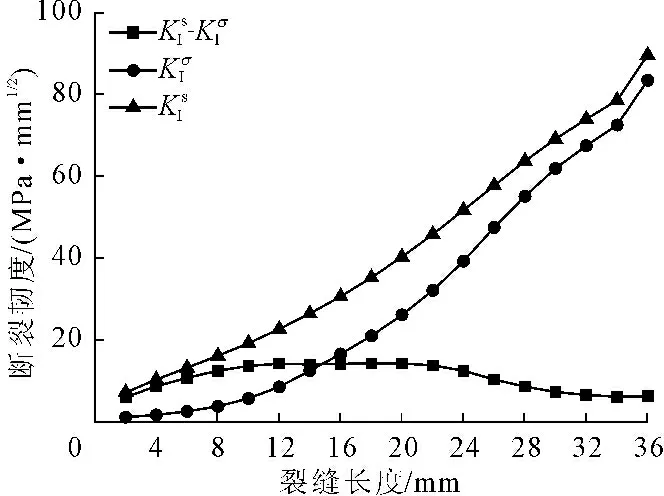
图6两种作用产生的的应力强度因子

AASHTO和ASTM两个标准试验方法推荐，约束圆环试验中早龄期混凝土的开裂通过钢环压应变的突然滞回确定。然而需要提出的是，钢环压应变的突然滞回仅仅代表着内部约束作用得到释放，不能够准确地反映出裂缝具体处于哪个破坏阶段。本文的数值计算结果显示，限制收缩下混凝土起裂后，裂缝只有在收缩和约束共同的驱动作用大于裂缝黏聚作用时，裂缝才会进一步扩展贯穿整个壁厚。在混凝土断裂力学中，混凝土的起裂是由材料特性引起，与结构的尺寸和边界条件无关；然而混凝土的失稳破坏点则是结构对外界条件的响应，是与结构的尺寸和边界条件紧密相关的。在本文的约束圆环试件中，混凝土裂缝在起裂后直接进入失稳破坏阶段并贯穿整个壁厚，说明起裂与失稳在同一时刻发生。但该计算结果只能代表本文所研究的混凝土材料与圆环试件几何情况，对于不同材料性能的混凝土及圆环试件尺寸，是否依然服从这一规律还有待进一步的研究。

4　结　论

本文在混凝土结构上施加虚拟温度场来模拟收缩作用，引入虚拟裂缝模型并在裂缝两侧施加黏聚力，还原混凝土裂缝尖端的应力场和位移场，分析收缩裂缝起裂和扩展全过程，分析得到如下结论：

(1) 对比约束圆环试件开裂时间，数值结果和试验结果吻合良好，说明本文采用的数值计算方法的可行性，同时说明可以引入虚拟裂缝模型来模拟约束圆环试验中混凝土的裂缝扩展全过程。

(2) 对于本文所采用的混凝土材料，约束圆环试件在混凝土起裂后，收缩效应产生的应力强度因子始终大于材料黏聚作用产生的应力强度因子，因此裂缝直接进入不稳定扩展阶段，钢环压应变的突然滞回标志着混凝土失稳破坏。

[1]Aashto. Standard practice for estimating the crack tendency of concrete:AASHTO Designation PP-34-99[S]. [s.l]:[s.n], 2006:179-182.

[2]Standard test method for determining age at cracking and induced tensile stress characteristics of mortarand concrete under restrained shrinkage: ASTM C 1581/C 1581M-09[S]. [s.l]:[s.n], 2009.

[3]巴恒静,苏安双,高小建,等.单面干燥条件下受约束高强混凝土的早期开裂研究[J].华南理工大学学报:自然科学版,2008,36(1):110-116.

[4]郑建岚,王国杰,王辉明.自密实混凝土自生约束收缩开裂性能试验研究[J].建筑材料学报,2010,13(5):607-612.

[5]高英力,龙杰,刘赫,等.粉煤灰高强轻骨料混凝土早期自收缩及抗裂性试验研究[J].硅酸盐通报,2013(6):1151-1156.

[6]高志楼,刘小艳,左俊卿,等.圆环法研究再生微粉混凝土收缩性能[J].粉煤灰综合利用,2012(2):6-10.

[7]Hossain A B, Weiss W J. Assessing residual stress development and stress relaxation in restrained concrete ring specimens[J]. Cement and Concrete Composites, 2004,26(5):531-540.

[8]Moon JM, Weiss W J. Estimating residual stress in the restrained ring test under circumferential dying[J]. Cement and Concrete Composites, 2006,28(5):486-496.

[9]Miltenberger M A, Attiogbe E K, See H T. Shrinkage cracking characteristics of concrete using ring specimens[J]. ACIMaterials Journal, 2003,100(3):239-245.

[10]Passuello A, Moriconi G, Shan S P. Cracking behavior of concrete with shrinkage reducing admixtures and PVA fibers[J]. Cement and Concrete Composites, 2009,31(10):699-704.

[11]Turcry P, Loukili A, Haidar K, et al. Cracking tendency of self-compacting concrete subjected to restrained shrinkage: experimental study and modeling[J]. Journal of Materials in Civil Engineering, 2006，18(1):46-54.

[12]Shah S P, Ouyang C, Marikunte S, et al. A method to predict shrinkage cracking of concrete[J]. ACI Materials Journal, 1998,95(4):339-346.

[14]Ouyang C, Shah S P. Geometry-dependent R-curve for Quasi-brittle materials[J]. Journal of the American ceramic society, 1991，74(11):2831-2836.

[15]中华人民共和国建设部.普通混凝土力学性能试验方法标准:GB/T50081-2002[S].北京：中国建筑工业出版社，2002.

[16]Testing of concrete-Part 8: Determination of drying shrinkage of concrete for samples prepared in the field or in the laboratory: ISO 1920-8[S]. [s.l]:[s.n], 2009.

[17]Bazant Z P, Wittmann F H. Creep and shrinkage in concrete structures[M]. [s.l]:[s.n],1982.

[18]Hillerborg A, Modéer M, Petersson P. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite element[J]. Cement and concrete research, 1976，6(6):773-781.

[19]Petersson P E. Crack growth and development of fracture zones in plain concrete and similar materials[R]. Lund, Sweden: Lund University, 1981.

[20]Yang Z J, Deeks A J. Fully-automatic modelling of cohesive crack growth using a finite element-scaled boundary finite element coupled method[J]. Engineering Fracture Mechanics, 2007，33(7):915-929.

[21]Ooi E T, Yang Z J. A hybrid finite element-scaled boundary finite element method for crack propagation modelling[J]. Computer Methods in Applied Mechanics and Engineering, 2010，199(17):1178.

Concrete Crack Initiation and Propagation Process in the Restrained Shrinkage Ring Test

LUO Hao1, RONG Hua2, YUAN Wenyan1, DONG Wei1

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering，DalianUniversityofTechnology,Dalian,Liaoning116024,China; 2.CentralResearchInstituteofBuildingandConstruction,Beijing100000,China)

The restrained ring test recommended by AASHTO and ASTM has been used for assessing the crack resistance of early-age concrete. In order to investigate the fracture mechanics of concrete in the ring test, shrinkage was simulated through applying the fictitious temperature filed on concrete based on thermal and structural analysis module in ANSYS. Combining with the stress analysis results, the crack location of concrete ring was determined, combining with the fictitious crack model, the crack propagation after initiation of ring specimens with circumference exposed was simulated. At the same time, the proposed method is proved feasible because concrete cracking time from numerical results and experimental results agree well. It was found that concrete directly go into unstable propagation stage after crack initiation in the restrained circular ring test, and the sudden drop of steel compressive strain represents onset of crack unstable propagation.

restrained shrinkage; fracture mechanics; fictitious crack model; crack propagation

10.3969/j.issn.1672-1144.2016.04.033

2016-03-25

2016-04-17

国家自然科学基金项目(51478083，51109026)

罗昊(1990—)，男(满族)，辽宁铁岭人，硕士研究生，研究方向为混凝土早龄期限制收缩破坏机理。

E-mail:luohao1021@126.com

TU528.1

A

1672—1144(2016)04—0168—05