基于ANSYS的寒冷地区大体积混凝土越冬保温研究
2016-09-19杜志达
张 豪,杜志达
(大连理工大学 建设工程学部, 辽宁 大连 116024)
基于ANSYS的寒冷地区大体积混凝土越冬保温研究
张豪,杜志达
(大连理工大学 建设工程学部, 辽宁 大连 116024)
利用大型通用有限元商业软件ANSYS提供的用户子程序USERMAT.F和UldFin.F,对ANSYS进行了二次开发,建立了弹性徐变本构模型,实现了大体积混凝土温度场和徐变应力场的计算,并通过具体算例验证其正确性。最后在此基础上运用等效散热系数法针对寒冷地区的大体积混凝土的越冬保温做了相应研究,为大体积混凝土的设计和施工提供一定的参考。
ANSYS;徐变应力;等效散热系数法;越冬保温
现如今,大体积混凝土已经广泛应用于我国土木水利工程建设中,在进行前期设计时需要重点考虑温控防裂问题,而混凝土结构开裂的主要因素是由温度徐变应力产生的[1-3]。混凝土的温控仿真研究主要包括温度场和徐变应力场的计算,这是一个非常复杂的分析过程[4-5]。为了解决这一问题,通常有两种办法,一是通过自编程序的方法进行相关计算,但是这些自编程序有着很明显的缺点,例如开发工作量大、维护较困难,前后处理功能不强等,因此并不是一个很好的选择[6-7]。另外一种是利用ANSYS、ABAQUS、MARC等商业软件强大的前后处理功能,通过对本构关系、边界条件等的设定以实现对相关问题的求解[8-9]。
ANSYS是功能齐全的大型通用有限元商业软件,国内众多企业和高校中的专家学者都在使用此软件,并且解决了很多科研难题。尽管ANSYS的通用性很强大,但不能解决所有用户的问题[10]。所以ANSYS提供了大量FORTRAN版本的用户子程序接口,用户可利用这些接口进行二次开发,实现各种复杂的应用功能。本文通过对ANSYS提供的用户子程序USERMAT.F和UldFin.F进行重新编写,建立了徐变本构模型,成功将混凝土徐变的相关理论在ANSYS中实现。并且在此基础上,结合某具体实例运用等效表面散热系数法对混凝土表面进行保温,针对寒冷地区的大体积混凝土的越冬保温情况做了相应研究。
1 基本原理
1.1混凝土徐变问题的有限元求解
设混凝土徐变度为
(1)
徐变应变增量为:

(2)
上式中,

(3)

(4)
应力增量与应变增量的关系为:

(5)
上式中,
(6)
(7)

单位刚度矩阵为:
(8)
可得非应力变形引起的单元荷载增量为
(9)
(10)
(11)
(12)
建立平衡方程,
∫∫∫[B]T{Δσn}dxdydz={Δpn}
(13)
整体的平衡方程为:
[K]{Δδn}={ΔPn}L+{ΔPn}c+{ΔPn}T+
{ΔPn}0+{ΔPn}s
(14)
其中,{ΔPn}L、{ΔPn}c、{ΔPn}T、{ΔPn}0、{ΔPn}s分别表示的是外荷载、徐变、温度、自生体积变形、干缩引起的节点荷载增量。
对式(14)进行求解,可以得到各节点位移增量{Δδn},将{Δδn}代入式(5),可得应力增量,最后将各个时间段的应力增量进行累加,获得最终应力:
{σn}=∑{Δσn}
(15)
1.2等效表面散热系数法的计算原理
大体积混凝土施工中必不可少的一种温控措施就是表面保温。温度原因造成的裂缝常常发生在大体积混凝土表面,这些裂缝基本都是由于外界气温骤降使得混凝土拉应力超限造成的,所以如何做好表面保温是防止这些裂缝产生的主要方法[11-12]。
现如今一般采用有限元法计算混凝土结构加保温材料的温度场,由于混凝土材料和保温板材料性能完全不同,在进行有限元建模的时候用不同单元进行模拟是几乎不可能的,所以一般通过等效表面放热系数法进行模拟研究。等效表面散热系数法的原理就是当混凝土表面添加保温材料时,依旧可以当作第三类边界条件,等效的方法是通过改变表面放热系数来表示保温材料的作用。等效表面散热系数的计算公式如下:
(16)
式中:Rs表示的是保温板总热阻;β表示的是最外层保温板在空气中的散热系数;hi表示的是保温板厚度;λi表示的是保温板导热系数。
因此,等效表面散热系数法就是根据已知的保温板厚度以及导热系数来计算其等效表面散热系数,通过这个方法来模拟保温板的效果,并且在进行有限元建模时不需要单独添加保温材料计算单元,复杂性很大程度的降低,计算效率也得到有效提高,在大体积混凝土结构表面保温模拟计算中已经较为成熟[13]。本文就用此方法模拟保温板的保温效果进行分析研究。
2 混凝土徐变问题在ANSYS中的实现
本文实现大体积混凝土温度徐变应力计算的二次开发需利用ANSYS提供的2个子程序:USERMAT.F和UldFin.F。
子程序USERMAT.F用于用户自定义材料本构模型的开发,本文中程序主要实现的有:定义混凝土徐变指数函数模型和弹性模量随龄期变化的函数;接收温度场计算得出的单元温度荷载;接收APDL中通过TBDATA定义的材料参数;建立徐变本构的一致切算子矩阵;更新每一个荷载步结束后的应力应变增量和状态变量。
子程序UldFin.F是计算干预子程序,用户可以利用该子程序开发自定义的运算功能,在每一荷载步结束的时候进行调用。本文利用计算干预子程序UldFin.F接收子程序USERMAT.F中的状态变量[ηn],并利用式(9)计算徐变引起的单元荷载增量{ΔPn}c。简明程序流程图如图1所示。

图1简明程序流程图
在应力场分析中,需要注意的是不能直接运用ANSYS的标准命令流杀死或者激活相应的单元。而是通过如下步骤实现应力场的求解:
(1) 在命令流中材料定义的时候中对每一层浇筑的混凝土赋予不同的材料号。
(2) 在命令流TBDATA定义用户自定义材料参数的时候,将每一层的开始浇筑时间定义为一种材料参数,同时在USERMAT.F子程序中利用Prop数组接受上述定义的材料参数,这样每一层的开始浇筑时间就成功导入USERMAT.F子程序中。
(3) 当计算时间小于当前混凝土层开始浇筑时间时,说明当前混凝土处于未浇筑状态,即在USERMAT.F子程序中将该层混凝土单元的弹性模量乘以一个极小值,并且在命令流中相应约束该层混凝土单元。
(4) 当计算时间大于当前混凝土层开始浇筑时间时,说明当前混凝土处于浇筑状态,即在USERMAT.F子程序中恢复其初始的弹性模量值,并且在命令流中相应删除该层混凝土单元的约束。
3 算例验证
算例1:为了验证上述程序的正确性,采用文献[14]中的一个应力松弛的例子进行验证,混凝土的材料参数如下:
弹性模量E=392 000MPa,热胀系数α=
1.0×10-5/℃,泊松比μ=0,

其中c1=2.04×10-6MPa-1,c2=2.55×10-6MPa-1,r1=3d-1,r2=0.3d-1。应变ε(t)=ε0,通过求解继效方程
(17)
可得:
σ(t)=Eε0(0.8475+0.0755e-3.24t+0.0770e-0.328t)
(18)
采用ANSYS有限元程序进行计算时,运用Solid185单元划分网格,施加均匀温升10℃,使其产生初始应力。计算完成后选取梁中部某一节点的计算结果与式(18)进行比较,结果如表1所示。

表1 理论解与ANSYS解计算结果
ANSYS计算应力随时间的变化过程如图2所示。

图2ANSYS计算结果
从表1和图2可以看出理论解和有限元的计算结果很接近,从而验证了本文所述方法的正确性。
算例2:采用文献[15]中在岩基上三层混凝土浇注块,用有限单元法计算其由于自身水化热的作用以及外界环境的冷却作用下的温度场和徐变应力场。混凝土浇筑块长度25.0 m,每层厚1.5 m,层间间歇7 d,浇筑完成后停歇200 d,总共历时214 d。相关计算参数如下:
混凝土导热系数λ=10.0 kJ/(m·h·℃)(MPa-1),导温系数a=0.004 m2/h,表面放热系数β=60.0 kJ/(m·h·℃),热胀系数α=1.0×10-5/℃。混凝土绝热温升为:
θ(τ)=25.0τ/(4.5+τ)
式中τ单位为d;θ(τ)单位为℃。
混凝土的弹性模量为:E(τ)=30000[1-exp(-0.4τ0.34)],单位为MPa。
混凝土的徐变度为:
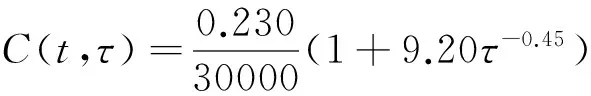
混凝土密度为ρ=2 326kg/m3,泊松比为μ=1/6;基岩弹性模量为E=30 000MPa,泊松比为μ=0.2,其他材料参数与混凝土一样。
分别采用Solid45和Solid185单元计算温度场和应力场,取四分之一模型进行计算,基岩厚度取6 m,沿高程方向基岩剖分了10层单元,混凝土每层剖分5层单元,共15层单元,有限元计算网格如图3所示。图4为混凝土中央剖面在浇筑后不同时间温度沿高程的分布,图5为混凝土中央剖面在浇筑后不同时间X方向正应力沿高程的分布。


图3 有限元计算网格

图4 混凝土中央剖面沿高程方向的温度分布图
图5混凝土中央剖面沿高程方向X方向应力分布图
由图4可以看出,在混凝土浇筑开始时,由于水泥水化热的作用,混凝土内部温度一直在升高,在20 d达到了最高温度12.8℃,发生在第三层混凝土中点靠下附近的位置,以后由于环境的影响整体温度开始下降,在214 d内部的最高温度只有2.1℃,发生在混凝土与基岩的交界位置。由图5可以看出,第1层混凝土是早期全断面受压,在第14 d达到了最大压应力为-0.94 MPa,发生在与上层混凝土交界点处,此后内部慢慢转化成拉应力,在100 d以后开始全断面受拉,在214 d达到了最大拉应力0.65 MPa,发生在中点位置;第2层混凝土与第1层基本一致,早期也是全断面受压,在第20 d达到了最大压应力为-0.90 MPa,同样也是发生在与上层混凝土交界点处,后期全断面收拉,在214 d达到了最大拉应力0.87 MPa,发生在与下层混凝土交界处的位置;第3层混凝土因顶面一直暴露在外,所以早期全断面受压,在第20 d达到了最大压应力为-0.54 MPa,发生在与下层混凝土交界点处,中期表面受拉而内部受压,后期表面受压而内部受拉,在159 d达到了最大拉应力0.64 MPa,发生在与下层混凝土交界点处。上述结果与文献[15]中计算结果误差很小,趋势一致,说明了本文方法的正确性。
4 工程实例
某严寒地区重力坝实际进度安排为第一年十月初开始浇筑, 到十一月初浇筑了5 m(分5层)后进入越冬保温期。前5层每层浇筑高度为1 m, 层间间歇为7 d。地区常年气温如表2所示。选取挤塑板为保温材料, 其散热系数为λ=0.108 kJ/(m·h·℃)。
采用有限元法对该重力坝越冬保温的过程进行模拟研究,计算在不同保温方案下的坝体温度场和徐变应力场,以确定合适的保温厚度。建立该坝坝体前五层有限元模型如图6所示,竖直向上为Y方向,上游到下游方向为X方向,具体保温方案如表3所示。取中央剖面典型点(如图6所示)相关数据以便分析。

表2 地区常年气温

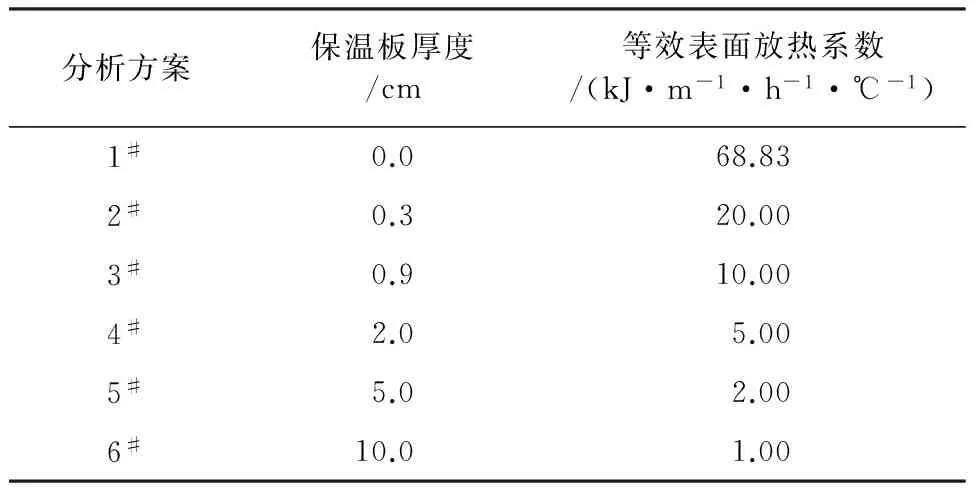
图6 前五层坝体有限元模型和典型点图
根据温度场计算结果,选取上游中点(点1)和内部点(点6)温度变化过程如图7、图8所示,两点的温差变化过程如图9所示。
由图7~图9分析可知,当β值越小时,坝体表面温度越高,内部散热越慢,内外温差也会相应的减小。当无保温时,内外最大温差达21.92℃,加保温之后典型点在越冬期间的温度变幅显著降低,当β=1时,内外最大温差也降到了17.11℃,保温的作用使得在越冬期内的温度变幅有效减小。


图7 点1温度变化过程图
图8点6温度变化过程图
对于应力场来说,主要考虑的是表面的最大拉应力。据《混凝土重力坝设计规范》[16](SL319-2005),取龄期180 d极限拉伸值及弹性模量,安全系数取1.5,计算得出混凝土块体允拉应力为1.52 MPa。由相关经验和计算结果分析后,选取越冬表面的三个点(点2、点3、点4)X方向的应力和上下游面的两个点(点1、点5)Z方向的应力在六种方案下的变化过程图如图10~图14所示。


图9 点1与点6内外温差变化过程图

图10 点2的X方向应力变化过程图

图11 点3的X方向应力变化过程图

图12 点4的X方向应力变化过程图

图13 点1的Z方向应力变化过程图
图14点5的Z方向应力变化过程图
由图11~图14可知,在无保温的情况下,坝体上下游面和越冬面会有比较大区域的超限拉应力区,最大拉应力达3.05 MPa,但随着β值越小时,各个典型点表面拉应力也相应的减小,当β=1时,表面最大拉应力降到了1.19 MPa,说明在寒冷地区越冬时对混凝土表面进行一定程度的保温是能够达到避免裂缝的目的。因此,为了控制最大拉应力在规范规定的限制内,根据所得结果数据我们可以通过选用的保温材料将上下游面的β值控制在1~2之间,即保温材料厚度为8 cm左右,顶面的β值控制在2~5之间,即保温材料厚度控制在4 cm左右,但对于边界处(点2、点4)因为双向散热应当适当增加保温,从而可以达到有效避免表面温度裂缝的目的。
5 结 论
(1) 本文利用UPFS和APDL对ANSYS进行了二次开发,通过对ANSYS提供的用户子程序USERMAT.F和UldFin.F进行重新编写,建立了弹性徐变本构模型,将混凝土弹性徐变方程的隐式解法引入ANSYS,实现了混凝土徐变问题的有限元求解,并且经过算例验证本文方法的正确性。
(2) 运用等效散热系数法对寒冷地区大体积混凝土施工期越冬保温进行了相关研究。在不同的保温方案下分别计算了大体积混凝土越冬保温的温度场和应力场,所得结果说明寒冷地区冬季温度很低,为了降低混凝土表面的温度梯度,避免拉应力过大造成裂缝的产生,必须选择合适的保温材料对暴露在外的混凝土进行施工停歇越冬保温处理。这将给大体积混凝土的表面保温对大体积混凝土施工期温控防裂提供一定的理论指导。
[1]高岳权,黄浩良,王佶,等.基于等效模量法与ANSYS计算混凝土徐变[J].武汉理工大学学报,2010,32(2):13-15.
[2]黄海东,向中富.混凝土结构非线性徐变计算方法研究[J].工程力学,2014,31(2):96-102.
[3]陈忠,张研,周红军.基于等效时间的混凝土徐变模型[J].河海大学学报(自然科学版),2011,39(3):302-305.
[4]胡磊,杨谈蜀.混凝土徐变影响因素及预测模型研究运用[J].煤炭技术,2010,29(4):113-116.
[5]卓旬,梅明荣.混凝土徐变计算理论和方法综述[J].水利与建筑工程学报,2012,10(2):14-19,40.
[6]王一凡,宁兴东,陈尧隆,等.大体积混凝土温度应力有限元分析[J].水资源与水工程学报,2010,21(1):109-113.
[7]路璐,李兴贵.大体积混凝土裂缝控制的研究与进展[J].水利与建筑工程学报,2012,10(1):146-150.
[8]王建,刘爱龙.ABAQUS在大体积混凝土徐变温度应力计算中的应用[J].河海大学学报(自然科学版),2008,36(4):532-7.
[9]李骁春,吴胜兴.基于ANSYS的混凝土早期徐变应力仿真分析[J].系统仿真学报,2008,20(15):3944-3947.
[10]李涛,张洵安,高娃.基于ANSYS的大体积混凝土温度应力的研究[J].混凝土,2010(12):43-46.
[11]田振华,郑东健,姚远,等.大体积混凝土寒潮期温度应力及表面保温分析[J].水电能源科学,2011,29(5):93-95.
[12]李潘武,曾宪哲,李博渊,等.浇筑温度对大体积混凝土温度应力的影响[J].长安大学学报(自然科学版),2011,31(5):68-71.
[13]丁兵勇,杨忠良,唐瑜莲,等.水电站厂房大体积混凝土温度应力分析与防裂措施[J].南水北调与水利科技,2015,13(2):362-365.
[14]唐崇钊.混凝土的徐变力学与试验技术[M].北京:水利电力出版社,1982.
[15]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.
[16]中华人民共和国水利部.混凝土重力坝设计规范:SL319-2005[S].北京:中国水利出版社,2005.
Winter Insulation of the Mass Concrete in Cold Area Based on ANSYS
ZHANG Hao, DU Zhida
(FacultyofInfrastructureEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China)
User subroutine USERMAT.F and UldFin.F of large commercial software ANSYS finite element were improved in this research. An elastic creep constitutive model was developed, temperature field and creep stress field calculations of mass concrete was acquired. Specific numerical examples were conducted to verify its accuracy. Finally, aimed at the problem of winter insulation of mass concrete in cold region, by means of equivalent thermal coefficient method, appropriate research had been carried out to provide some reference for the design and construction of mass concrete.
ANSYS; creep stress; the equivalent thermal coefficient method; winter insulation
10.3969/j.issn.1672-1144.2016.04.035
2016-03-20
2016-04-10
张豪(1993—),男,安徽马鞍山人,硕士研究生,研究方向为大体积混凝土温度控制。E-mail:zhanghaodut2016@163.com
杜志达(1967—),男,内蒙古赤峰人,教授,主要从事水利工程施工模拟方面的研究工作。E-mail:duzhida@dlut.edu.cn
TU37
A
1672—1144(2016)04—0177—06
