基于bi-LWCA-ENN煤与瓦斯突出危险性预测*

付　华，司南楠，鲁俊杰，王雨虹，徐耀松

（辽宁工程技术大学电气工程与控制工程学院，辽宁葫芦岛125105）

基于bi-LWCA-ENN煤与瓦斯突出危险性预测*

付华*，司南楠，鲁俊杰，王雨虹，徐耀松

（辽宁工程技术大学电气工程与控制工程学院，辽宁葫芦岛125105）

为了提高煤与瓦斯突出的预测精度，以实现准确、可靠的瓦斯突出危险性预测，提出一种双层狼群算法（LWCA）优化Elman神经网络模型进行模式分类与预测，建立煤与瓦斯突出的双层LWCA-ENN预测模型。分析煤与瓦斯突出机理和影响因素，提取相关数据样本，筛选稳定的特征子集作为特征向量训练模型，算法通过对Elman神经网络的权值、阈值寻优，建立了基于bi-LWCA-ENN算法的预测模型并结合矿井监测数据进行实例分析。试验结果表明：煤与瓦斯突出的bi-LWCA-ENN模型稳定性好，收敛速度快，有效地实现了瓦斯突出危险性预测。

煤与瓦斯突出危险性；双层狼群算法；Elman神经网络；特征选择

煤与瓦斯突出是含有瓦斯媒体突然破坏并释放出其弹性潜能和瓦斯潜能的一种矿井瓦斯动力现象。分析并综合基于各类假说的煤与瓦斯突出机理，煤与瓦斯突出过程的实质是在卸压区，煤层破裂体在地应力与瓦斯压力的耦合作用下发生失稳，即煤与瓦斯突出受地应力、瓦斯压力作用、以及煤岩特性等多因素的影响，这些因素相互制约，与瓦斯突出存在着非线性映射关系。为了保障突出矿井安全生产，提高经济效益，必须对突出进行有效的防治。

在对煤与瓦斯突出研究的进程中，提出了多种突出预测方法，静态法［1］是首先应用在工作面煤与瓦斯的预测中，从现场工作面瓦斯煤体中提取某种量化指标而确定危险性，如钻屑量S，此类预测方法其结果不能完全代表整个预测步长范围内和煤体稳定前整个时期内的突出危险性，容易出现延期突出现象；因此静态预测法逐渐被动态连续预测取代，声发射技术［2］因煤岩裂隙的产生和扩展以弹性波的形式产生能量辐射而发展运用；文献［3］对受载煤岩体及瓦斯解吸流动等情况下的电磁辐射进行了深入的研究，提高了预测精准率；声发射和电磁辐射以及微震法［4］，由于在矿井恶劣环境下采集到的信号受干扰及噪声影响大，加之智能算法的发展，决策树、支持向量机（SVR）、人工神经网络（极端学习机、RBF神经网络）［5-9］等逐渐应用于煤与瓦斯突出预测中。

本文采用Elman神经网络［10-11］算法进行输入数据与瓦斯突出危险性之间的非映射关系研究，通过多组样本训练模型以形成一定的规则而预测新数据，而对于其参数优化，传统的优化算法如遗传算法［12］、粒子群算法等在后期收敛速度慢，易陷入局部最优或精度不高等缺陷，因此本文提出一种双层狼群［13］优化算法，其在迭代中不断淘汰适应度差的狼群，解决上述算法不足。各个矿井影响煤与瓦斯突出的因素不尽相同，对各项指标的敏感性也存在差异，将特征选择［14-15］FS（Feature Selection）应用于敏感指标的筛选中，既可以减小维数灾难，又防止出现高维小样本的数据稀少造成的过拟合现象，提高泛化能力，加快Elman神经网络学习过程。

1　煤与瓦斯突出指标参数量化

依据现代采矿理论的危险性预测原理可表述为：基于对突出的理论认识，在分析影响煤与瓦斯突出影响因素基础上，对各影响因素进行定量化分析，确定煤与瓦斯突出危险性的预测准则［16］，应用网络模型确定预测区域的危险性，对煤与瓦斯突出的危险性进行分类，划分煤与瓦斯突出危险区、突出威胁区和无突出危险区。

在井下采掘过程中，根据引起煤与瓦斯突出危险性主要因素，选择适当的危险性预测敏感指标，依次选取综合指标、突出预兆指标、瓦斯压力：MPa、瓦斯含量：m3/t、顶板岩性：（渗透率）/%、开采深度：m、坚固系数等十项指标作为该矿井煤与瓦斯突出的基础参数。

1.1综合指标

在煤层区域性突出危险性预测时，可按下列两个综合指标判断：

式中，K、D为煤层的突出危险性综合指标；H为开采深度，m；Δp为软分层煤的瓦斯放散初速度；f为软分层煤的平均坚固性系数；p为煤层瓦斯压力。

结合表1，如果实测的指标D、K值均小于临界值，并且未发现其它异常现象，则该工作面无突出危险性，否则有突出危险。

表1　突出危险性预测综合指标D、K参考值

1.2突出预兆指标的定量化

突出预兆是工作面是否具有突出危险性最表象也是最直接的外在特征，不同突出预兆对应的突出防线大小为突出风险度R，则

式中，R为不同突出预兆对应的突出风险度；T为不同类型突出预兆对应的突出风险率，如表2所示；ξ为突出预兆严重程度系数。

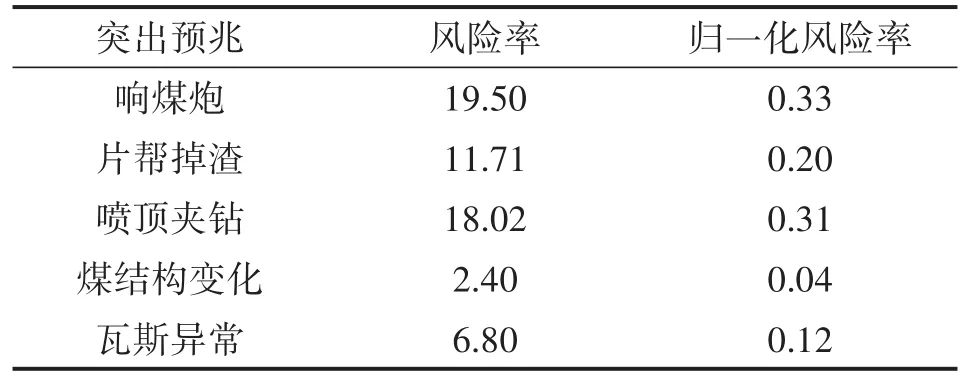
表2　不同突出预兆的风险率

严重程度等级对应严重程度系数分别如下：等级为严重时，严重程度系数为2，等级为中等时，严重程度系数为1，等级为轻微时，严重程度系数为0.5。

1.3瓦斯含量

在煤岩巷道打孔，测定煤屑的瓦斯解吸指标值（用以测定煤样装入仪器前煤样的瓦斯解吸量W），在接入钻屑的同时保存一罐煤样密封送入实验室测定煤样中的残余瓦斯含量X残余，则煤层的原始瓦斯含量为

K1值和损失瓦斯含量W之间的关系式：

式中，K1为比例系数，煤样自煤体脱落暴露在大气1 min期间每克煤的瓦斯解吸量，；Q为每克煤的瓦斯解吸量，mL/g；W为煤样自装入仪器之前的解析瓦斯量，mL/g；t为煤样在仪器内的解析时间，min。

1.4瓦斯压力

直接测定煤层瓦斯压力时从围岩巷道向煤层打直径为50mm～75mm的钻孔，孔中放测压管，将钻孔密封后用压力表直接进行测定，对于难以直接测量的条件下采用间接的测量方法，其测定瓦斯压力的工作根据瓦斯含量测定，根据朗格缪尔曲线方程表达式（6）计算，a、b为吸附系数。

2　基于Bagging稳定的瓦斯突出特征选择

现有的特征选择［14-15］方法更侧重于特征选择结果的高分类或聚类性能，而忽略了特征选择结果的稳定性，训练样本集中的样本数据变化或含有噪声特征，加之Elman神经网络算法的不稳定性，尤其在瓦斯突出预测中，新的数据在不断收集并输入到网络模型中，若模型输入的样本特征随着新数据的更新而差异大，模型的分类率下降，因此应将特征选择的稳定性度量和分类的准确率综合考虑，得到一个稳定性强分类准确率高的模型。

图1　特征选择稳定性图解

设原始数据D=｛X，Y｝，X∈RN×s，原始特征集合F=｛f1，f2，…，fs｝，特征选择的过程为：f（F:X，Y）→｛F′｝，f（·）为特征选择算法，F′⊂F为所选择的特征子集，为所选的特征个数；在原始数据D上新增样本 D′=｛X′，Y′｝构成新的样本集 D1，X′∈RN′×s，D′与D同分布，在样本集D1上使用特征选择算法 f（·）进行特征选择，得到特征子集F1′，若使特征选择的稳定性好，即｛F′｝≈｛F1′｝，如图1所示为特征选择稳定性图解。

结合Bagging集成学习方法，特征选择操作方案：用bootstrap从N个样本中抽取m个候选特征子集（m=μN，0＜μ＜1），特征选择算法，通过误差RMSE得到m个基特征选择器，输入新的样本X，根据m个基特征选择器，进行分类并返回预测值，与真实值进行比较，若划分正确记第i个特征子集各特征一票，对于包含m个特征排序结果的集合，利用加权投票得到的集成特征选择结果为：

式中，ω（·）表示加权函数，l=1，2，…，n，每个特征的最终排序值是在搜索排序结果中的排序值，再根据式（7）获取集成特征排序的结果。

3　基于bi-LWCA-ENN的煤与瓦斯突出模型建立

3.1基于狼群算法的ENN参数编码

狼群神经网络训练时，每个狼群个体Xi代表神经网络各层的连接权值和阈值，编码采用实数矢量形式，以图2（a）的三层神经网络拓扑结构为例，狼群个体Xi的编码形式如图2（b）所示，编码长度L 由Elman神经网络各层的节点数r、s1、s2决定。

图2　狼群算法编码形式

Elman神经网络训练时，模型的训练精度通过训练误差RMSE来衡量

训练误差越小，代表网络对瓦斯突出训练样本的拟合过程更为充分，得到的神经网络模型精度越高。

狼群神经网络模型训练过程中，狼群个体的适应度与该个体对应的模型下的训练误差有关，适应度与训练误差值构成线性关系：

根据式（10）知，训练误差越小，则个体的适应度值越大，在狼群算法中，适应度值越大，则表明狼群个体在寻优问题上表现越优。

3.2bi-LWCA-ENN算法方法论

领导狼狼群算法LWCA（Leader Wolves Colony Algorithm）的基本思想：在瓦斯突出预测模型中，网络参数问题的解是狼群搜索空间内的最佳个体位置，所有狼群个体都对应着Elman网络的训练误差函数决定的适应值，适应值越大，狼群的位置越好。

随机初始化网络参数｛ω，β，b，ϖ，b′｝，根据适应度函数计算狼群适应值，并以此选取q个适应度值最佳的个体竞选首狼，竞选狼附近h个位置中的第l个点第d维的位置xld（1≤l≤h）：

领导狼搜索猎物，当狼发现猎物且猎物不在领导狼位置，狼群就会偏离领导者，更新个体位置zid：

领导狼找到食物，向导狼包围猎物，在［0，1］内产生随机数rm，θ为预先设定的阈值，并对狼群个体位置进行越界处理，参数更新为：

在优化搜索初期运行阶段个体在大范围内以较大的包围步长快速搜索到全局最优邻域，而在最优邻域附近的个体以较小的包围步长变为局部搜索，每次迭代结束都移除最差的m匹狼，再随机生成m匹狼，可以精确、快速的搜索到全局最优解。

其中，rand是［0，1］内均匀分布的一个随机数，stepa和stepb分别是搜索步长和移动步长，ra为包围步长，maxt为最大迭代次数，ramax和ramin分别为最大最小的包围步长。

上述的LWCA算法中涉及参数较多，对模型起主要影响的是搜索步长stepa和包围步长stepb，其取值缺乏依据或经验公式，选取不当模型的训练误差无法有效收敛，种群个体之间协同寻优功能易失效，因此将双层狼群神经网络用于瓦斯突出预测模型中。

基于双层狼群优化ENN模型具体步骤如下，其操作流程图如图3所示。

①对bi-LWCA-ENN预测模型进行初始化，包括生成外层狼群初始种群，编码长度为2，编码元素依次对应内层狼群算法的搜索步长stepa和移动步长stepb；生成内层狼群种群，用于bi-LWCA-ENN模型参数的优化。

②输入经过特征筛选后的突出训练样本，计算bi-LWCA-ENN模型的实际输出与期望输出，根据式（10）计算内层狼群个体适应度值。

图3　bi-LWCA-ENN预测模型示意图

③进行双层狼群算法优化Elman神经网络。内层狼群移动公式的搜索步长stepa和移动步长stepb由外层个体决定，内层个体依据式（11）～式（15）进行模型参数的更新，当达到内层迭代次数停止，并将最优的内层狼群个体适应度值赋予对应的外层个体，作为该外层个体的适应度值，考虑到模型的复杂度，外层其余个体依据式（10）计算适应度值，搜索使模型误差最小的搜索步长stepa和移动步长stepb的取值，外层所有个体通过式（10）更新一次种群后而进行内层种群寻优，直到达到外层最大迭代次数停止，内外层迭代次数分别设为800、20（参考经验选取值及重复试验，800、20次既能在迭代完成时满足训练误差要求，又避免造成训练时间过长）。即外层种群每更新一次，内层种群就更新800次。

④Elman神经网络训练结束，得到适应度最好的狼群位置即获得bi-LWCA-ENN最优参数矢量｛ω，β，b，ϖ，b'｝作为预测模型的权值、阈值。

⑤输入测试样本，特征选择后作为bi-LWCAENN模型的输入向量，判断模型的预测能力。

4　煤与瓦斯突出预测试验及分析

①实验数据来自开滦矿业集团钱营矿2074综采工作面的KJ90N煤矿安全综合监测系统，截取2015年6月份中的400个实测数据作为研究对象。在进行模型训练之前进行特征筛选，其涉及的相关设置如下：选用浮动广义向后搜索策略，将预测模型的误差RMSE作为评价指标，特征选择结果体现在图4中。

图4　特征选择与未经筛选特征模型误差曲线

特征选择结果的稳定性是通过评价不同特征选择结果的相似性来度量的，采用特征排序向量作为特征选择算法输出，为第i个特征子集中特征的排序，m个特征子集中共筛选出n个特征，Spearman相关系数为 fi和 fj的相似性如式（16），通过式（17）得到整体特征的稳定性，如图5所示。

由图4知，未经特征提取的样本数据在预测过程的后半段预测精度产生了明显的偏差，相对误差达到了7.65%，说明未经特征提取的样本的模型时效性有限。图5为当样本集发生微小扰动时，两种不同特征选择方法稳定性的比较，图中曲线1为本文所用的Bagging特征筛选方法，其筛选稳定性为0.8～0.9之间，筛选结果保持一致或比较接近，相比曲线2，曲线2的稳定性会随样本集中的扰动而波动，且稳定值较低。

②结合煤与瓦斯突出的数据进行分类与预测，分析所提出的bi-LWCA-ENN的训练、测试能力。瓦斯突出输入样本经筛选后特征维数为6，选择K折交叉验证的测试方法，并确定Elman神经网络的结构：输入层、输出层节点数分别为6+1=7、1，人为选定隐含层节点数8个，狼群外层个体编码长度为L=2，编码元素为内层狼群算法参数搜索步长stepa和移动步长stepb，初始化外层狼群规模N=100，候选领导狼q=5，候选领导狼h个方向大小为h=4，最大竞选次数 maxdh=10，搜索步长 stepa=1.5，移动步长stepb=0.9，被淘汰狼个数m=5，阈值θ=0.2；初始化内层狼群规模N=200，最大竞选次数maxdh=15，搜索步长和移动步长随机赋予初值，其它参数同上。在上述参数的设置下进行bi-LWCA-ENN模型对瓦斯突出输入样本数据的训练。

利用训练集重复进行试验，得到狼群神经网络搜索步长和移动步长的平均值和标准差如表3所示。

表3　内层狼群移动步长和搜索步长选取结果

内层狼群选取上述参数的平均值重复训练，并与固定参数取值stepa=1.5，stepb=0.9的狼群算法进行对比，训练误差RMSE的临近值设为0.1%，训练、测试的平均结果如表4所示。

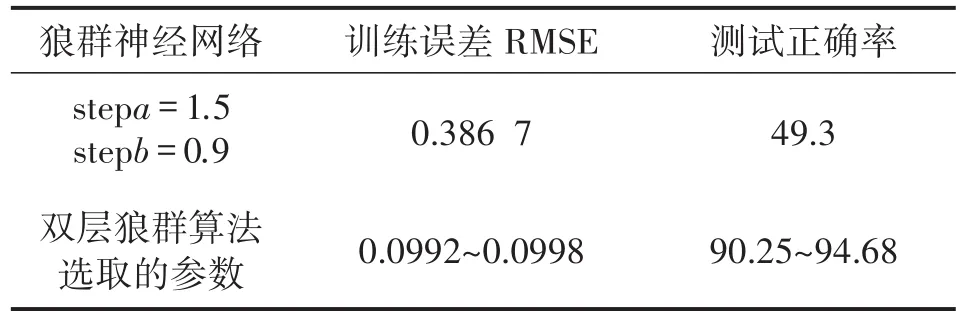
表4　瓦斯突出数据的训练测试结果对比　单位：%

从表3可知，Elman神经网络模型在双层狼群算法优化下选取的参数的训练误差都位于误差临界值0.1%以下，在规定的迭代次数内，均达到了设定的训练精度要求，而在固定取值 stepa=1.5，stepb=0.9下，网络训练误差收敛值为0.386 7%，远大于临界值，可见在一般参数取值下，狼群神经网络训练不足，因而无法有效识别测试样本，测试的正确率为49.3%，远小于双层狼群算法选取参数下神经网络的测试正确率。图6为bi-LWCA-ENN模型训练收敛误差曲线，在起初训练阶段，该模型能以较快的下降速度收敛，在后期bi-LWCA-ENN能稳定的收敛在低误差段，误差精度高。根据突出危险性概率划分（危险区概率预测指标＞0.6，、威胁区概率预测指标为0.6～0.3、安全区概率预测指标＜0.3），分别取不同区域的03#（威胁区）、07#（危险区）、12#（安全区）、21#（危险区）、29#（安全区）、36#（威胁区）共6组数据进行预测，其结果参照图7，可知本预测方法可有效地实现煤与瓦斯突出的危险性预测。因此，该方法可作为一种有效的突出危险性预测方法。

图6　瓦斯突出双层LWCA-ENN收敛曲线

图7　测试样本的预测结果

5　结论

（1）基于数据扰动的Bagging集成方法，结合单特征选择器对样本进行特征选择，与未经特征筛选的训练样本比较表明，通过特征筛选，原始特征集合中的不相关特征和冗余特征被删除，且有效提高特征选择算法的稳定性，提高算法精度。

（2）将双层狼群优化算法引入到瓦斯突出危险性预测模型中，在整个训练进程中模型能以较快的速度搜索全局最优解，充分改善了ENN模型的学习速度慢、陷入局部极值等缺点，且bi-LWCA-ENN模型能够提高系统的跟踪能力，结合煤矿历史数据并经MATLAB仿真试验验证了模型的预测性能，相比于传统的狼群、粒子群优化算法能在收敛后期平稳、快速的收敛到误差精度范围内，适用于煤与瓦斯突出危险性预测中，此方法对煤矿防突具有重大意义。

［1］Dingqi Li，Yuanping Cheng，Lei Wang，et al.Prediction Method for Risks of coal and Gas Outbursts Based on Spatial Chaos Theory Using Gas Desorption Index of Drill Cuttings［J］.Mining Science and Technology（China），2011，21（3）：439-443

［2］单亚锋，孙朋，徐耀松，等.基于PSO-SVM的煤岩声发射源定位预测［J］.传感技术学报，2013，26（03）：402-406.

［3］王恩元，李忠辉，何学秋，等.煤与瓦斯突出电磁辐射预警技术及应用［J］.煤炭科学技术，2014，42（06）：53-57+91.

［4］朱权洁，李青松，李绍泉，等.煤与瓦斯突出试验的微震动态响应与特征分析［J］.岩石力学与工程学报，2015，34（S2）：3813-3821.

［5］李定启，程远平，王海峰，等.基于决策树ID3改进算法的煤与瓦斯突出预测［J］.煤炭学报，2011，36（04）：619-622.

［6］Qiao Meiying，Ma Xiaoping，Lan Jianyi，et Al.Time-Series Gas Prediction Model Using LS-SVR Within a Bayesian Framework［J］. Mining Science and Technology（China），2011，21（1）：153-157.

［7］Xin Yuanfang，Jiang Yuanyuan，Zhang Xuemei.Gas Outburst Prediction Model Based on Empirical Mode Decomposition and Extreme Learning Machine［J］.Recent Advances in Electrical& Electronic Engineer ing，2015，8（1）：50-56.

［8］付华，李文娟，孟祥云，等.IGA-DFNN在瓦斯浓度预测中的应用［J］.传感技术学报，2014，27（02）：262-266.

［9］Zhang Ruilin，Ian S.Lowndes.The Application of a Coupled Artificial Neural Network and Fault Tree Analysis Model to Predict Coal and Gas Outbursts［J］.International Journal of Coal Geology，2010，84（2）：141-152.

［10］付华，谢森，徐耀松，等.基于ACC-ENN算法的煤矿瓦斯涌出量动态预测模型研究［J］.煤炭学报，2014，39（7）：1296-1301.

［11］付华，刘雨竹，李海霞，等.煤矿瓦斯浓度的CAPSO-ENN短期预测模型［J］.传感技术学报，2015，28（5）：717-722.

［12］郭金栋，王恩元.基于量子免疫遗传算法的煤与瓦斯突出神经网络预测［J］.山东科技大学学报（自然科学版），2014，33（6）：69-75.

［13］吴虎胜，张凤鸣，吴庐山，等.一种新的群体智能算法——狼群算法［J］.系统工程与电子技术，2013，35（11）：2430-2438.

［14］Li Hui，Zhang Shu，Wang Xia.The Technique of Gas Disaster Information Feature Extraction based on Rough Set Theory［J］.Journal of Computers，2013，8（4）：983-989.

［15］Wu Shiyue，Guo Yongyi，Li Yuanxing，et al.Research on the Mechanism of Coal and Gas Outburst and the Screening of Prediction Indices［J］.Procedia Earth and Planetary Science，2009，1 （1）：173-179.

［16］Song Weihua，Zhang Hongwei.Regional Prediction of Coal and Gas Outburst Hazard Based on Multi-Factor Pattern Recognition ［J］.Procedia Earth and Planetary Science，2009，1（1）：347-3.

付华（1962-），女，辽宁阜新人，教授，博士生导师，博士（后），主要研究方向为煤矿瓦斯检测、智能检测和数据融合技术。支持国家自然科学基金2项、支持及参与国家863和省部级项目30余项，发表学术论文40余篇，申请专利24项，fxfuhua@163.com；

司南楠（1990-），女，山东淄博人，辽宁工程技术大学电气与控制工程学院硕士研究生，主要研究方向为检测技术及其自动化装置，1546538885@qq.com。

Prediction of Coal and Gas Outburst Risk Based on bi-LWCA-ENN*

FU Hua*，SI Nannan，LU Junjie，WANG Yuhong，XU Yaosong
（College of Electrical and Control Engineering，Liaoning Technical University，Huludao Liaoning 125105，China）

In order to improve the prediction accuracy of coal and gas outburst，realize the accurate and reliable gas outburst danger prediction，this paper put forward a method that use bi-Leader Wolves Colony Algorithm（LWCA）to optimize Elman neural network for pattern classification and prediction，and model of coal and gas outburst was established by bi-LWCA-ENN algorithm.On the analysis of the mechanism and influencing factors of coal and gas outburst based on the data samples that extracted by application of feature selection as the characteristic vector，a bi-Leader Wolves Colony Algorithm（LWCA）was merged with Elman neural network to optimize weight and threshold，with the data of mine actual monitoring to experiment and analysis.The results show that the bi-LWCA-ENN model of coal and gas has good stability and fast convergence rate，realized the gas outburst prediction effectively.

coal and gas outburst；bi-wolves colony algorithm；Elman neural network；feature selection

TP391；TP212

A

1004-1699（2016）08-1222-07

EEACC：723010.3969/j.issn.1004-1699.2016.08.017

项目来源：国家自然科学基金项目（51274118）；辽宁省教育厅基金项目（L2012119）；辽宁省科技攻关项目（2011229011）

2016-01-13修改日期：2016-03-15