函数列收敛性判别法的动态与静态性教学法

刘炎，张学奇，陈文辉

(广东金融学院 应用数学系,广东 广州 510521)



函数列收敛性判别法的动态与静态性教学法

刘炎，张学奇，陈文辉

(广东金融学院 应用数学系,广东 广州 510521)

以“动态”和“静态”的对立统一思想来讨论函数列与函数项级数的收敛性与一致收敛性，据此，我们可以对于函数列收敛性判别法提供一种新的教与学的方式。

函数列;函数项级数;收敛性;一致收敛性

函数列的收敛性与一致收敛性是函数的重要性质，它在级数的收敛理论中扮演着相当重要的角色。一般的数学分析书籍都列出了许多判定方法，但是根据定义判定函数列的收敛性与一致收敛性的过程过于繁琐，学生很难掌握其本质，更难以灵活地用于实际判断。事实上，这种困难在于没有很好的把握收敛性定义与各种判定方法中的动静思想。我们可以注意到，无论从定义，命题还是习题，“任给”与“存在”是一对经常并行出现的量词。“任给”是先动后静，“存在”是依赖着动而静，是一种动静结合的逻辑体系，可以说贯穿于整个分析学。本文从教学实践出发，强化动态和静态的思想来分析函数列的收敛性问题，得出这两种状态下收敛与一致收敛性的判定方法，并给出相应的例题；最后，将此思想用运于函数项级数的一致收敛的判断，收到了很好的教学效果。

1　判别函数列收敛与一致收敛的方法

按照函数列收敛的定义，当我们考察函数列{fn(x)}在某区间I内的收敛性的时候，我们通常需要考察这个函数列在这个区间内是否逐点收敛于某一函数f(x)。但是在实际应用的过程中，运用此方法比较繁琐。因此，我们引入静态的思想。将x固定在x0之时，我们称之为静态。而若函数列{fn(x)}所处静态之时且同时令n→∞,若函数列fn(x0)收敛于f(x0)，那么我们认为函数列{fn(x)}收敛。归结以上，我们有以静态方法判断函数列收敛的结论：

在考察函数列{fn(x)}在某区间I内的一致收敛性的时候，判定过程更为复杂。以往，我们先要求出极限函数f(x)，再找出一个N=N(ε)使得函数列与极数的差值|fn(x)-f(x)|<ε。我们引入动态的思想判定函数列的一致收敛性。当x为在区间I上任意变化的时候，我们称之为动态。若函数列{fn(x)}所处动态之时，并使n→∞，若函数列fn(x)的极限为f(x)，那么函数列{fn(x)}一致收敛。通过以上分析，我们得出以动态方法判断函数列一致收敛与不一致收敛结论：

事实上，函数列一致收敛的动态性反映为x在区间I上的任意变化性，也即存在一个不依赖x而只依赖于控制函数差值的ε的充分大的数N=N(ε)，使得当n>N=N(ε)时，有|fn(x)-f(x)|<ε成立。这种N不依赖x的变化性就是动态性的反映。x变，N不依赖x而变，由动而导致静正是一致收敛的核心。并由此，我们有得到一致收敛的否定性结论：

2　收敛与一致收敛判别方法的应用

而固定x=x0，同时运用洛必达法则可得

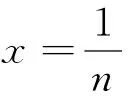
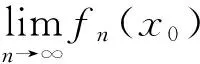
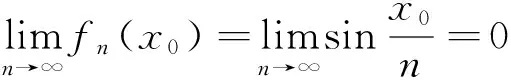
同理，固定x=x1，也有相同的结果。因此根据结论1，发现在[0，1]和(-∞，+∞)内函数列{fn(x)}收敛。以下分别讨论函数列{fn(x)}在这两个区间内的一致收敛性：

(1)并不固定x的取值，让其在区间[0，1]内变化。我们发现无论x如何变化，总有x≤n成立。因此无论x在[0，1]中如何变化，当n→∞时

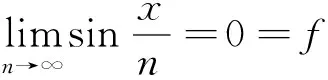
(2)当x∈(-∞,+∞)时，我们让x在区间内变化，使其处于动态的过程。同时，使x充分大，选取x与n满足x=n+1，那么

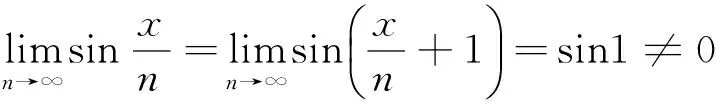
最后，我们将上述动态和静态的思想应用于函数项级数收敛性与一致收敛性的判断。我们通过一条例题来说明这种方法的应用。

首先在区间[0，1)上选取x0并固定x=x0，那么会发现

3　结论

动态与静态思想贯穿整个分析体系，从数列极限、函数极限、函数连续性、导数与微分积分、数列与函数列的收敛性、数项级数与函数项级数的收敛性等等，可谓无处不在，从而数学分析教学中对动态与静态思想方法值得我们深入细致的研究。在数学分析的教学中，始终要向学生阐明这些基本结论与概念中蕴涵的动与静的辨证关系，并且立足于让学生以动的方法去理解，以静的方法去解决，这样才能真正掌握其要领。

[1] 徐志庭，刘名生，冯伟贞.数学分析(二)[M].北京:科学出版社,2009.

[2] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,2003.

[3] 吕通庆.一致收敛与一致连续[M].北京:人民教育出版社,1981.

(责任校对王小飞)

10.13582/j.cnki.1674-5884.2016.08.020

20160518

国家自然科学基金项目资助(11201087)；广东省教育厅教改课题(2015GXJK103)；广东金融学院校级重点培育学科“应用数学”；广东金融学院创新强校工程“温度依赖于溶解度的热对流模型的解的性态研究”；2015广东省教育质量工程—金融数学示范专业以及广东省教育厅—数学建模团队项目资助

刘炎(1980- )，男，湖南澧县人，副教授，博士，主要从事偏微分方程研究。

G0171

A

1674-5884(2016)08-0062-03