洲滩钉螺垂向迁徙对水位变化的滞后响应研究

李凌云，卢金友，范北林，王家生

(长江科学院 a.河流研究所; b.水利部江湖治理与防洪重点实验室，武汉　430010)



洲滩钉螺垂向迁徙对水位变化的滞后响应研究

李凌云a,b，卢金友b，范北林a,b，王家生a,b

(长江科学院 a.河流研究所; b.水利部江湖治理与防洪重点实验室，武汉430010)

河湖洲滩是血吸虫唯一中间宿主——钉螺的主要分布区域。洲滩钉螺垂向迁徙与水位密切相关，但一般滞后于水位变化，以往研究没有考虑这一滞后现象，难以准确把握钉螺垂向迁徙规律。为了准确预测洲滩生境条件变化后钉螺的垂向分布高程，对钉螺迁徙过程进行概化，推导了水位变化后钉螺理论分布高程的计算模型，揭示了钉螺随水位变化的迁徙规律。研究结果表明：①钉螺分布高程随着水位增加而增加，随水位降低而降低；②水位上升时钉螺分布高程与水位之间距离有减小趋势，水位下降时钉螺分布高程与水位之间距离有增加趋势。利用洞庭湖区东口洲滩实测资料进行检验，结果表明基于滞后响应原理的钉螺垂向迁徙预测模型能够较准确地预测洲滩水位变化后密螺线的分布高程。

钉螺；带状分布；垂向迁徙；水位；滞后响应

1　研究背景

血吸虫病是世界卫生组织(WHO)确定的6大重点热带病之一，全球现有76个国家地方性流行血吸虫病，目前约6亿人口受血吸虫病威胁，感染人口约2亿[1]。河湖洲滩是血吸虫唯一中间宿主——钉螺的主要分布区域。长期的野外观察表明，河湖滩地的钉螺一般生长在洲滩水位线以上一定高程的位置，呈带状分布。按钉螺分布密度水位高程从高到低可依次定义为上有螺线、密螺线和下有螺线，钉螺生存在下有螺线和上有螺线之间，且以密螺线附近分布密度最大。在下有螺线高程以下和上有螺线高程以上的地带，因滩地湿度、植被等环境不满足钉螺生长条件，少见钉螺分布。上述现象已为广大血防科研工作者所认知，但限于当前认识水平，目前对钉螺带状分布特征的研究以定性描述为主，部分学者采用数学统计方法直接拟合钉螺分布与生境要素之间量化关系[2-3]，但从理论上建立钉螺分布高程调整模型的研究尚未见报道。如何准确预测洲滩生境条件变化后钉螺的垂向分布高程这一问题一直没有得到很好地解决。

20世纪90年代，杨先祥等[4]、徐兴建等[5]、张威等[6]先后通过室内试验研究了钉螺在水中的沉降、起动规律，建立了钉螺沉速及起动流速计算方法，总结了钉螺随水流扩散的3种基本运动方式。这些成果为进一步研究钉螺洲滩迁徙扩散规律奠定了重要基础。同时，我国血防工作者在三峡水库下游血吸虫病疫区针对钉螺分布情况开展了大量的野外调查工作[7-16]，获取了大量的野外观测资料，印证了钉螺在河湖洲滩的一般分布规律。秦建新等[17]基于RS与GIS技术，研究了洞庭湖区水文、气候、土壤等自然环境与钉螺分布之间的关系及钉螺空间分布的特征。Zheng等[18]定性分析了三峡水库运行与下游洲滩钉螺扩散的关系，认为洞庭湖洲滩钉螺扩散受三峡水库运行影响明显，而鄱阳湖洲滩钉螺扩散受到的影响相对较小。姚孝明等[19]以洞庭湖区目平湖为例，比较三峡建坝前后环境变化并分析对钉螺分布的影响，结果表明湖泊洲滩钉螺分布与水位变化有明显关系。何家昶等[20]研究了三峡建坝后长江安徽段水位变化对钉螺分布的影响，认为水位变化将会造成低高程滩地钉螺扩散。此外，部分研究者基于数学统计手段，研究描述钉螺分布规律的数学表达方法。苏德隆[21]较早提出了水网型钉螺的负二项分布规律，随后很多研究均认为钉螺的相关分布是负二项分布，张志杰等[22]拟合不同季节的钉螺数据，并与负二项分布进行了比较分析，结果表明，广义负二项分布比负二项分布能更好地反映钉螺分布的复杂性。Seto等[2]收集了鄱阳湖区1998—2002年间的水位、天气及钉螺数据，并进行了线性关系分析。马巍等[3]以洞庭湖为例定量分析了洞庭湖区钉螺分布与城陵矶站汛期平均水位的线性相关关系。

可以看出，上述研究主要基于野外观测和调查，对观测结果进行规律性总结。部分研究者在此基础上，利用数学统计方法进行了进一步分析，以期建立钉螺分布与生境要素之间的数学关系。总体来看，这些研究基于某一个或几个疫区野外实测资料，其成果适用范围也仅限于相应区域，而得到的数学关系以直接数学拟合为主要手段，属于经验性成果，未能从钉螺本身的生态学习性以及生境要素变化规律出发，缺乏理论基础，成果适用范围有限。

本文基于生态学理论，结合野外观测资料分析了钉螺的一般分布规律，对水位变化后洲滩钉螺垂向迁徙过程进行概化，通过数学方程描述概化后的迁徙过程，从理论上建立了水位变化条件下洲滩钉螺垂向迁徙的滞后响应模型，得到了钉螺生长高程与水位高程之间函数关系。

2　理论模型建立

长期的野外观察表明，洲滩钉螺一般生长在水位以上一定高程的位置，呈带状分布，且随水位变化而变化。通常情况下，钉螺平均密度沿垂直于等高线方向呈近似正态分布，即中间密度大，两端密度小。图1给出了洲滩钉螺分布的概化示意图。

图1　钉螺生长分布示意图Fig.1　Zonal distribution of snails on bottomland

图1中显示了钉螺在洲滩呈带状分布的特点。从水位z高程往上，依次为下有螺线zd、密螺线zm及上有螺线zu。钉螺生存在下有螺线zd和上有螺线zu之间，且以密螺线zm附近分布密度最大，而在zd高程以下和zu高程以上的地带，因河岸带土壤湿度、植被等环境不满足钉螺生长条件，没有钉螺分布。也就是说，钉螺总是生长在一定的土壤湿度范围内，当水位变化后，土壤湿度分布将发生变化，适合钉螺生长的湿度带位置随之改变，钉螺则自动迁徙到新的适合其生长的湿度带。将钉螺及洲滩生境看成一个开放系统，密螺线及上、下有螺线是系统的内部变量，而水位高程为系统的外部控制变量。当外部控制变量发生变化时，即系统受到外部条件干扰作用，系统会立即作出响应，表现为内部变量的调整变化。当系统外部条件不变且持续作用足够长时间时，系统将调整达到相对平衡状态。图1可以看出，密螺线是洲滩钉螺带状分布的中心地带，作为洲滩钉螺分布位置的代表变量最为合适，因此下面以密螺线高程为代表变量，分析密螺线随水位高程变化的响应调整过程，如图2所示。

图2　密螺线随水位变化的响应调整过程示意图Fig.2　Adjustment of the altitude line of the densest distribution of snails in response to water level fluctuation

对于图2所示的密螺线响应模式，作如下假定：①假定水位的扰动是突然发生的，之后维持足够长的时间不变；②密螺线的平衡状态值记为适螺线ze，且ze是一个常数，由扰动后的水位高程唯一决定；③密螺线在水位变化后立即作出响应，没有延时时间，但到达新的平衡状态的时间滞后于水位扰动时间；④初始的密螺线可以是原有的平衡状态值，也可以是处于不平衡状态的任何值。

图2所示的密螺线的响应调整过程可以用如下微分方程描述：

(1)

式中：zm是密螺线高程；ze是适螺线高程，理解为密螺线在长时间尺度上的平衡值；βm是密螺线的调整变化速率；t是时间。

图2和式(1)表明，不同的洲滩水位高程对应着唯一的最适合钉螺生长高程线，即适螺线。当水位高程发生变化后，新的适螺线随即确定，密螺线逐步往适螺线靠近直至最终重合。图2和式(1)还体现出了密螺线调整速度逐步减缓的特点，即：由于适螺线具有钉螺生长的最佳生境条件，当水位变化后的初始时刻，钉螺所处的生境条件最差，钉螺由密螺线向适螺线移动的驱动力最强，表现为钉螺由密螺线向适螺线靠近的速度最快；随着钉螺逐步向适螺线移动，其生境条件也逐步得到改善，向适螺线移动的驱动力也逐步减弱，表现为向适螺线靠近速度逐步减缓。这一特点符合钉螺生长的生态学原理，也表明了图2和式(1)所描述的钉螺密螺线调整模式是合理的。当水位高程变化并确定后，式(1)中适螺线视为常数，由此可得式(1)以zm为变量的通解为

(2)

式中zm0为t=0时zm的值。

式(2)即为密螺线随水位变化进行响应调整的基本模式，它描述了密螺线在水位变化后的一定时段内的调整路径。当水位再次变化后，密螺线沿着该路径的调整将立即终止。水位变化后对应的适螺线ze和水位变化前的密螺线高程值zm将重新给出新的调整路径。

自然条件下，河湖洲滩水位的变化十分频繁，因此很可能存在密螺线尚未调整到达适螺线的位置，水位就发生新的变化，适螺线的位置也随之变化。但适螺线变化后密螺线的调整仍然可以用图2和式(1)给出的调整模式描述，只是t=0时刻密螺线的初始值zm0尚未达到平衡值而已。这种情况可以理解为调整模式的迭代模式，如图3所示。

图3　密螺线调整多时段迭代示意图Fig.3　Iterative model of multi-period adjustment of the altitude line of the densest distribution of snails

由图3可知，在水位z0条件下，密螺线调整至zm0状态。此时水位扰动，密螺线由zm0开始调整。经过Δt时段后，密螺线调整至zm1，由此，式(2)可改写为

(3)

式中：ze1为第1个Δt时段内的水位所决定的适螺线高程；zm1为经过第1个Δt时段的调整后密螺线的高程；Δt为水位变化的时间段。

在下一个Δt时段内，将上一时段末的密螺线高程zm1作为这一时段的初始值，则经过Δt时段的调整后，时段末的密螺线高程zm2可表达为

(4)

式中ze2为第2个Δt时段内的水位所决定的适螺线高程。将式(3)代入式(4)可得

(5)

依此类推，将上一时段的结果作为下一时段的初始条件，逐时段递推，经过n次计算后得

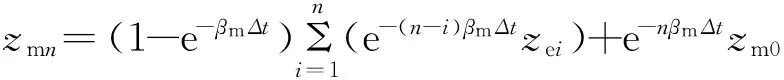
(6)

式中:n为迭代时段数；i为时段编号。

(7)

由于各时段的适螺线高程ze由相应时段的水位高程z唯一决定，即ze为z的函数即

(8)

因此可以看出，最终第n个时段末的密螺线高程zmn是由包括当前时段在内的一系列时段内的水位高程zi所共同决定的。也就是说当前的密螺线高程不仅与当前的水位高程有关，同时也与前期一定历史时期内的水位高程有关。至于密螺线高程受影响的前期时段长度，则与具体河湖的水流、土壤、气候、植被等条件有关，需要根据实测资料综合分析确定。

3　模型应用

3.1实用模型推导

适螺线是具有钉螺生长所需的最佳生境条件的位置，与洲滩水流、土壤湿度、气候、植被等众多因素有关，之前分析表明，众多因素中水位高程是影响适螺线高程的决定性因素，结合实测资料分析，假设适螺线高程ze与当前水位高程z之间的函数关系为

(9)

式中:α为>0的待定系数，与具体河湖滩地的土壤特性、植被种类等条件有关，计算时需根据实测资料确定；z*为近似于当地河湖洲滩春、秋季(钉螺生活周期)平均水位的参数，一般为较为稳定的常数。

需要说明的是，汛期河道水位一般均维持较高状态，此时洲滩往往被洪水所淹没。实际上，钉螺的带状分布生长规律在汛期已经被打破，大量的钉螺漂浮在水面或附着在芦苇等挺水植被的顶端度汛，因此汛期的适螺线实际上已经不再存在，但为了模型计算方便，汛期仍采用式(9)计算虚拟的适螺线高程，并参与模型计算。通常条件下，血吸虫病疫区的查螺频率为每月1次，因此进行模型计算时，可以将1个月作为一个计算时段长度。但在汛期由于洪水水位较高，一般不需要进行查螺，因此整个汛期均无查螺记录，实际上汛期也没有钉螺由密螺线向适螺线移动调整的过程。为了模型计算的连续性，之前仍采用式(9)计算虚拟的适螺线高程，但若模型中继续沿用汛期的实际时间作为计算时段长度显然是不合适的。对于河湖洲滩而言，汛期最重要的特征是洪水水位较高淹没洲滩土壤，从而使得土壤充分浸润，尤其是汛末最后1个月水位高程的影响最为明显，而淹没时间本身则不再是最重要的因素。基于这一认识，同时便于计算方便，取汛期计算时段长度为1个月，即与非汛期计算时段长度一致。

根据实际经验，先取n=2，即考虑包括当月在内一共3个月水位的影响。式(7)可以展开为

zm2=(1-e-βmΔt)(ze2+e-βmΔtze1)+e-2βmΔtze0。

(10)

为便于计算，令：pm=e-βmΔt，将式(9)一并代入上式，可得

(11)

实际查螺过程中，密螺线zm与水位z之间高差往往是关注的重要参数之一，令：Δz2-1=z2-z1，Δz1-0=z1-z0，式(11)改写为

(12)

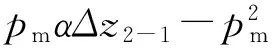
3.2模型检验

洞庭湖区是我国长江中下游血吸虫病主要疫区之一。本文选择洞庭湖区岳阳市君山区东口洲滩2008年10月至2010年12月实测钉螺监测数据，采用距离钉螺监测点(东口洲滩)约10 km处(见图4)的城陵矶水文站的水位数据。根据所收集的钉螺监测资料和水位资料，可得式(12)应用于东口洲滩时的参数取值为：α=0.16，z*=21.4，pm=0.1，由此得到东口洲滩密螺线高程与水位差之间高差计算公式为

zm2-z2=-0.84z2-0.016z2-1-

(13)

图4　东口洲滩和城陵矶水文站地理位置Fig.4　Geographical sketch map of Chenglingji station and Dongkou bottomland

图5　计算值与实测值对比散点图Fig.5　Correlations between computed results and field survey data

利用式(13)即可计算东口洲滩密螺线高程与当前水位高程之间差值，图5为计算值与实测值对比散点图，可以看出，数据点基本分布在45°线附近，表明计算值与实测值符合较好，二者相关系数R=0.73。需要说明的是，本文用于模型检验计算的数据量相对较少，且数据收集范围集中在岳阳东口洲滩。下一步可广泛收集资料，针对不同类型洲滩，进一步验证模型的准确性和适用性。

4　结　论

(1)通过概化钉螺对水位变化的响应和调整过程，提出了钉螺垂向迁徙对水位变化的滞后响应物理模式，建立了水位变化后钉螺垂向迁徙的滞后响应计算模型。

(2)基于所建立的滞后响应模型，从数学上表达了钉螺滞后于洲滩水位变化的垂向迁徙过程，即钉螺分布高程随着水位增加而增加，随水位降低而降低，水位上升时钉螺分布高程与水位之间距离有减小趋势，水位下降时钉螺分布高程与水位之间距离有增加趋势。

(3)利用所建立的滞后响应模型，计算了洞庭湖区东口洲滩2008—2010年钉螺分布高程，计算结果表明，基于滞后响应原理的钉螺垂向迁徙预测模型能够较准确地预测洲滩水位变化后密螺线的分布高程。

[1]龚震宇,杨小平.全球血吸虫病流行概况[J].疾病监测,2011,26(6):504.

[2]SETO E Y,WU W,LIU H,et al.Impact of Changing Water Levels and Weather on Oncomelania hupensishupensis Populations,the Snail Host of Schistosoma japonicum,Downstream of the Three Gorges Dam[J].Eco Health,2008,5(2):149-158.

[3]马巍,廖文根,匡尚富,等.洞庭湖钉螺扩散与水情变化规律[J].长江流域资源与环境,2009,18(3):264-269.

[4]杨先祥,潘庆燊.钉螺和螺卵静水沉降及运动方式的实验研究[J].动物学杂志,1994,29(6):1-3.

[5]徐兴建,潘庆燊.钉螺静水沉速公式的推导与建立[J].湖北预防医学杂志,1996,7(3):26-28.

[6]张威,陈伟.钉螺起动流速试验研究[J].长江科学院院报,1994,11(4):23-29.

[7]陈雪峰,储成忠,杜怡芳,等.安徽石台县钉螺分布现状与调查[J].热带病与寄生虫学,2010,8(2):88-90.

[8]陈燕国,蔡建新,彭国忠,等.2005年华容河钉螺分布现状及防治对策[J].中国血吸虫病防治杂志,2006,18(6):441.

[9]柯永文,韩世民,杨和奎.安徽池州市贵池区钉螺及感染性钉螺调查与分析[J].热带病与寄生虫学,2011,9(2):91-94.

[10]钱泽祥,王晓可.枞阳县2002—2009年钉螺调查[J].安徽预防医学杂志,2009,15(6):468-469.

[11]汪为春,詹惕,朱应富,等.马鞍山市辖区8条通江河道钉螺调查[J].热带病与寄生虫学,2008,6(3):162-163.

[12]王柏勇.嵊州市1996—1998年钉螺调查结果[J].浙江预防医学,2001,13(12):20.

[13]王富宽,谭敏华.2000—2001年玉山县感染性钉螺调查[J].中国血吸虫病防治杂志,2003,15(2):156.

[14]吴建平,肖妙青.株洲市血吸虫病新疫区钉螺调查报告[J].中国血吸虫病防治杂志,2000,12(3):164.

[15]吴子松,赵联国,毛勇,等.2002—2003年西昌邛海湖盆沟渠钉螺调查[J].中国血吸虫病防治杂志,2004,16(5):359-362.

[16]向钢,郭志贤.益阳市血吸虫病流行区垸外洲滩易感地带钉螺调查分析[J].中国血吸虫病防治杂志,2000,12(4):252.

[17]秦建新,谭子芳,张春.洞庭湖区江滩钉螺分布的环境因子及空间特征——基于RS/GIS的研究[J].自然灾害学报,2008,17(4):19-27.

[18]ZHENG J,GU X,XU Y,et al.Relationship between the Transmission of Schistosomiasis japonica and the Construction of the Three Gorge Reservoir[J].Actatropica,2002,82(2):147-156.

[19]姚孝明,周应彩,赵正元,等.目平湖洲滩钉螺分布与水位及植被变化的关系[J].实用预防医学,2008,15(3):641-644.

[20]何家昶,张世清,张功华,等.三峡建坝后水位变化对皖江流域血吸虫病流行影响的预测研究[J].中国媒介生物学及控制杂志,2002,13(6):448-449.

[21]苏德隆.苏德隆教授论文选集[M].天津:天津科学技术出版社,1995：71-101.

[22]张志杰,彭文祥,SENGHUAT O,等.广义负二项分布对钉螺分布的拟合[J].中国卫生统计,2008,25(1):2-6.

(编辑：王慰)

with the descending of water level.According to the field data at the Dongkou bottomland of Dongting Lake,the calculation method based on the delayed response for predicting the snails’ distribution elevation was tested,and the results showed that the relationship between the snails’ vertical distribution and the water level alteration established in this paper can be used to accurately predict the snails’ distribution elevation.

Delayed Response of Snails’ Vertical Migration onthe Bottomland to the Changed Water Level

LI Ling-yun1，2,LU Jin-you2,FAN Bei-lin1，2,WANG Jia-sheng1，2

(1.River Department,Yangtze River Scientific Research Institute,Wuhan430010,China; 2.Key Laboratory of River-Lake Regulation and Flood Control of Ministry Water Resources, Yangtze River Scientific Research Institute,Wuhan430010,China)

As the only intermediate host of schistosome,snails generally live at the bottomland of lakes.The vertical migration of snails on the bottomland is closely related to the water level but usually delayed to the water level alteration,which has not yet been considered in previous studies.As a result,the snails’ vertical migration is always difficult to describe or predict accurately.A generalized model for the changes of snails’ vertical distribution was proposed in this study,and a calculation method is developed for predicting the theoretical distribution elevation of snails in the presence of altered water level.The calculation method reveals that:1).the elevation at which snails are distributed increases with the rise of water level and decreases with the decline of water level; 2).the distance between the snail distribution elevation and the water level decreases with the rising of water level,and increases

snail; zonal distribution; vertical migration; water level; delayed response

2015-04-08；

2015-06-15

国家自然科学基金项目(51209015，51339001)

李凌云(1982-)，男，土家族，湖南慈利人，高级工程师，博士，从事河流动力学及河流生态方面的研究，(电话)027-82829145(电子信箱)lilingyunhq@163.com。

10.11988/ckyyb.201503782016,33(08):1-5，10

TV853

A

1001-5485(2016)08-0001-05