此减非彼简
——一次监测引发对简便运算教学的思考
2016-09-18浙江仙居县实验小学317300
浙江仙居县实验小学(317300) 方 芳
此减非彼简
——一次监测引发对简便运算教学的思考
浙江仙居县实验小学(317300)方芳
计算教学占据小学数学教学的半壁江山,所以简便运算是计算教学的“重头戏”。在市监测和学校普测的错例统计基础上,对学生的错因进行细致剖析,同时针对教学中存在的问题,提出简便运算教学的措施,以使学生获得更好的发展。
简便运算错例分析对策意识技巧练习
我非常有幸全程参与了台州市小学数学四年级的监测活动,共收到有效样本9213份。我们选择了一些典型的题进行全方位的分析,其中一道计算题引发了我的思考。如下:

本题的得分率为64.6%,与预计的难度系数有一定的距离。学生呈现的比较典型的错误如下式(1)~(3),也有属于口算的错误,如下式(3)和(4)。

简便运算教学相较于老教材而言,课时、类型都减少了,但是很多教师也深切地感悟到:花的时间最多,不少学生对定律、性质掌握的很好,但是在实际应用中却错误百出。为了更好地寻求教学的突破点,我再一次在学校里组织小测试,并以此为切入点进行分析,寻找错因和对策。
一、错例回眸
参与测试的为五年级的432名学生,因为统计的内容过多,现只摘录其中出错率较高的几题予以呈现。如下:
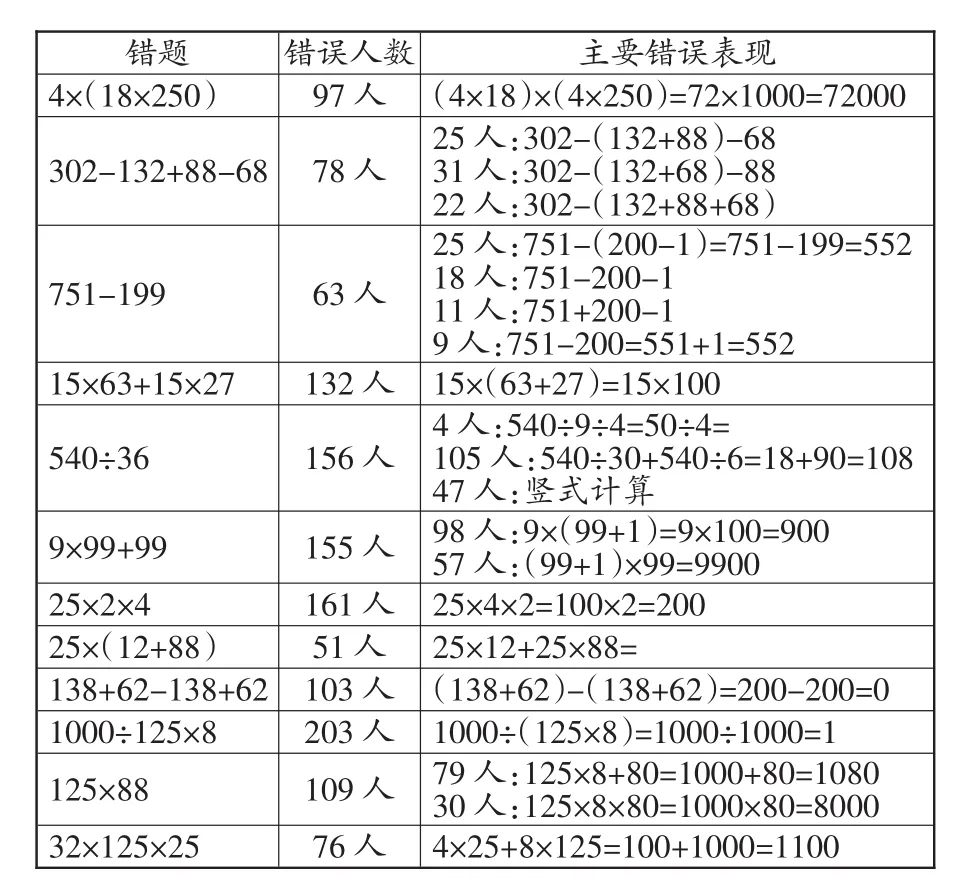
二、错例透视解读
透析这些错例,大致可归为以下几个方面。
1.张冠李戴——定律易混淆
学生主要出现两种情况,一是对运算定律混淆不清,二是对运算性质理解不深。简便运算是一种高级的混合运算,是混合运算的技巧,而运算的五大定律是简便运算的支撑。如有些算式看上去与某些定律、性质相似,于是有的学生盲无目的,只要相似就用方法去套用解决,从而失去了观察、分析和思考的能力。例如,乘法分配律和结合律容易产生混淆,它们的表现形式十分相近,导致一些学生造成误判。如4×(18×250)=(4×18)× (4×250),一些学生没有抓住乘法分配律和结合律的特征进行计算;计算302-132+88-68时,一些学生容易出现三种情况,即302-(132+88)-68、302-(132+68)-88、302-(132+88+68),都源于错误运用减法的性质。
2.马步不稳——口算能力弱
简算的一个重要基础是建立在学生对数的敏感与口算的快、准上。从错误率最高的15×(63+27)=15×100= 1500、540÷36=540÷9÷4=50÷4、300÷15=11……10等算式中可以看出,学生口算不熟练、准确率低。口算能力弱,导致学生对数的判断能力不强。如计算540÷36中有47人选择了笔算,无法发现这题可以简便计算。这说明我们在教学简便计算中重在方法的引导与运用,忽略了对学生口算基本功的训练。
3.大鱼不吃小鱼——思维已定式
强化口算训练,有时容易造成思维定式。如在学生的错例中出现9×99+99=9×100=900,这是由于在学生的印象中,99比9凑整更常见。为巩固学生的简便运算,教师往往进行专项训练,帮助学生及时巩固所学知识,使学生形成和熟练口算的技能,结果反而让学生在不知不觉中形成思维定式。如25×2×4,学生马上会把25和4联系在一起进行计算,为什么他们想不到直接算呢?一学生告诉我:“其实我知道还是按照原来的运算顺序计算简便的,可是不用运算定律,到时说我不是简便计算呀!”
4.盲人摸象——观察忽整体
小学生受年龄的制约,对事物无法进行全面的统筹。如有百分之十几的学生这样计算:138+62-138+62= (138+62)-(138+62)=200-200=0,1000÷125×8=1000÷ 1000=1。这里,学生看到哪些数据可以凑整的,就不管三七二十一先凑整,而忽略灵活运用定律和运算顺序,说明学生缺乏整体的意识,不会从整体上看算式的特征和考虑运算顺序。如监测中有75+225÷(18-3)一题,学生看到75+225就先凑整计算,从而导致计算错误。
三、思考与对策
简便运算一般以怎样简便就怎样计算的形式出现,不仅需要灵活运用运算定律、性质,更需融合学生的计算能力、思维品质、情感态度等。那么,在实际教学中,我们教师应该注意什么呢?
1.在大计算观中培养学生简算的意识
简算是四则运算中的一部分,教师应该把简算融入整个计算教学中。其实,简算并非是在运算定律学习后才出现的,它从学生开始学习计算时就孕伏其中。如“凑十法”,实际上就是加法交换律和加法结合律的不自觉使用。又如12×21=12×20+12×1=240+12=252,这里乘法分配律的使用以及乘加、乘减等,都要在不知不觉中渗透简算的意识。同时,简算意识的培养并不只是体现在计算中,也存在于解决问题探讨最优的方法、统计与概率、空间与图形中,让学生消除为简算而简算的定式。
简便运算的书写虽然没有简便,可它能令我们的计算思维和方法更简便,但因为简便运算容易让学生失分,导致教师把注意力集中在简便的方法上,认为学生能运用运算定律进行简便计算就是完成教学任务了。因此,教师应把简便计算置于整个教学体系之中,让学生了解为什么要简便计算及简便计算有什么优点,这样学生才会将简便计算作为解决问题的一个重要策略。
2.在算理理解中深化技能的掌握
运算的五大定律与性质是重要的基础知识,是简便计算的重要依据。如果学生没有真正理解运算定律、性质,那么简便运算就是无本之木、无源之水,最后只能“照葫芦画瓢”了。而新教材将运算的五大定律集于一体,有利于学生进行横向比较。
(1)依托生活情境,理解运算定律。
新教材最明显的特点之一就是关注数学的现实背景。教师应领会教材编者的这一意图,用好教材,借助数学知识的现实原型,结合学生熟悉的问题情境,激活学生的生活经验,引导学生体会运算定律的现实背景,理解所学的运算定律,构建个性化的知识。如学习加法交换律时,教师可以利用执教班级的男(35人)女(31人)生人数来让学生计算总人数(66人),并提问:“为什么都是66人?”这样使学生明白:不管是“男生人数+女生人数”,还是“女生人数+男生人数”,算的都是这个班的总人数,其结果是一样的。同时,在教学中,教师要让学生思考:“加法交换律需要通过例子去证明,那么需要哪些例子去证明呢?”如大的数、小的数、特殊数(比如0)等,只有通过充分的素材研究,才能让学生在研究中明白刚才的猜想是正确的。
(2)用自己的话来理解运算定律、性质。
对于运算的定律与性质,教材中虽然给了我们明确的定义,但一些学生只限于背定律,而在运用上缺乏灵活性。因此,教师不妨引导学生用自己的话来加深理解所学的运算定律和性质。如乘法分配律和乘法结合律,除了让学生通过不完全归纳法理解外,还可以让学生从条件、角度等不同方面进行理解。如只有两个数相加和相减,再去乘一个数,才可以用乘法分配律;乘法结合律是三个数相乘,无需运用加减法。又如加法交换律,要先算加法,再交换位置,才能适用。
3.在对比练习中促进技巧的形成
(1)教材对比,丰富教学。
目前,新版本的教材比较多,每一版本的教材都有不同的呈现方式或情境,那么这些教材变的是什么、变的理由是什么?我们只有读懂这些,才能促进我们的教学,使学生真正理解所学知识。如在浙教版教材中是常见的类型题,但在新教材中不再出现,面对这一类题目,学生无从下手,而这能促进学生对乘法分配律的理解。像“多退少补”等类型的题目新教材不再出现,但生活中经常见到,导致学生在计算751-199等算式中容易出错。按四年级下册教学用书上的建议,本单元只有10个课时,这样的教学只能是点到即止,知识点过于集中,所以教师有必要补充课时数。
(2)练习对比,提升技巧。
在学生理解定律后,计算技能需要在对比中进一步提升。如125×88,选一选下列哪种方法是正确的,为什么?A.125×8+80;B.125×8+125×80;C.125×8×80;D.125×8× 11。通过选择比较,不仅让学生感知到有些问题可以有多种方法解决,而且使学生明白乘法分配律的本质特征。又如,仔细观察,判断下列算式哪些可以进行简便计算:(25+75)×(26+14)。这样的对比辨析,让学生明确有些计算看似可以运用定律进行简算,但实际上却改变了计算的结果,还有必要对运算定律进行灵活的运用。如第一层次计算:35×34+65×34;第二层次计算:36×34+65×34;第三层次计算:350×34+65×340和70×17+65×34。对于第一层次计算,学生可能会主动进行简便计算;对于第二层次计算,不妨要求学生用简算的方法去进行计算,同时让学生观察比较第二层次计算和第一层次计算有什么不同;第三层次可以检测有多少学生能主动进行简算。教师应积累学生容易上当的、容易混淆的题,并经常进行训练,切实提高学生简算的水平。
4.三步走,形成技巧
在教学简便运算中,我们发现可以分为这样的三步:一找,二变,三估。一找,即从算式的特征找方法,先从整体到局部,由运算符号到算式中数的特征进行全方位的观察,再确定计算的方法。二变就是改变运算的方式,但要保证计算的结果不变,即调用所学的运算定律和性质重组运算顺序,达到变难为易的目的,使整个计算的过程口算化。三估是让学生通过估算可以判断方法是否正确,如125×88≈120×90=10800,就可以直接判断另两个选择1080和8000是错误的。
总之,新教材中简便运算的内容虽然减少了,但不等于教师减轻了负担,更不等于教学可以简单化,反而给予了教师更大的思考空间。如果说简便运算是一曲歌,希望我们在新课程的简算教学中,越唱越优美!
(责编蓝天)
G623.5
A
1007-9068(2016)20-036
