激活经验，主动建构

江苏无锡市花园实验小学（214000）李梅芝



激活经验，主动建构

江苏无锡市花园实验小学（214000）李梅芝

数学课程标准把获得数学活动经验与理解数学知识、掌握数学技能、感悟数学思想方法共同作为义务教育阶段学生数学学习的重要目标之一。由两个课时的递进式教学设计阐述了在教学中如何避免学习过程的简单重复，如何让学生对数学知识深刻理解并感悟数学思想方法后，达成数学活动经验的获得、丰富、内化，完成知识经验的构建。

数学活动经验积累内化递进

学生数学活动经验在数学活动中产生，是他们主动参与数学活动的过程和结果。但是这个经验的获得不是一蹴而就的，与个体的认知水平、情意状态以及个体参与活动的程度密切相关，而且一次性经验很容易随着时间的流逝被淡忘，需要有积累、丰富和内化的过程。

“用计算器探索规律”是苏教版小学数学第八册的内容。这一单元主要引导学生借助计算器探索积的一些变化规律和商不变的规律，并运用这些规律进行简便计算和解决一些简单的实际问题。第一课时是“用计算器探索积的变化规律”，教学重点是使学生探索并掌握一个因数不变，另一个因数乘几，得到的积等于原来的积乘几的变化规律，让学生充分经历和体验探索数学规律的一般策略和方法，即提出猜想、举例验证、发现规律、运用规律，进而发展数学思维。第二课时“用计算器探索商不变的规律”，教学目标与第一课时大同小异，两节课的结构也基本相同。对这样的两节“相似”的课，如何设计才能避免简单重复的学习过程，达成“把在第一课时学生积累的学习经验在第二课时加以运用，并完成拓展、内化经验，感悟思想，发展思维”的一个递进式的教学目标呢？为此，我们数学组进行了积极的研究。

第一课时“用计算器探索积的变化规律”教学片断：

1.提出猜想

师：积的变化会存在怎样的规律呢？我们就以36×30为例进行探索。请用计算器算算它的积是多少。

生：1080。

师：如果其中的一个因数不变，另一个因数乘一个数，得到的积可能会有什么变化呢？比如，因数36不变，把另一个因数30乘2，得到的积和原来的积相比，会有什么样的变化呢？请想一想、猜一猜，然后在小组里交流你的想法。

出示：

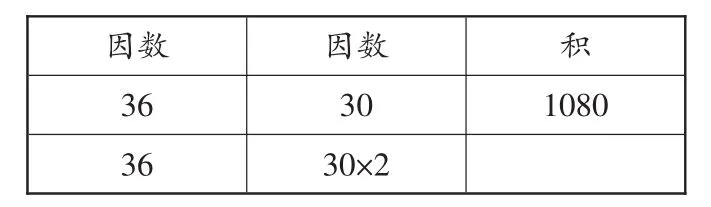
生1：一个因数36不变，另一个因数30乘2，得到的积等于原来的积乘2。

生2：一个因数不变，另一个因数乘几，得到的积等于原来的积乘几。

2.引领学生举例验证

师：从表格上看，一个因数36不变，另一个因数变化后是几？（60）现在的积又是多少？（2160）一个因数不变，另一个因数乘2，根据猜想，现在积应该等于原来的积乘2，那2160是否等于1080乘2呢？也请你算一算。你是怎么算的？

生3：2160÷1080=2。

生4：1080×2=2160。

师：这个例子符合我们的猜想吗？

师：又如，一个因数不变，另一个因数乘10，或者乘8，或者乘100，积又会有什么样的变化呢？请你再次验证。验证时注意因数和积的变化。

师：以上4个例子符合猜想吗？

生：符合。

3.学生自主举例验证

师：仅仅通过这4道题目能证明我们的猜想一定正确吗？（再举些例子来证明）

师：请同学们举出乘法算式来验证猜想。

生5：

生6：

（学生汇报交流）

师：大家举的例子符合我们的猜想吗？有没有谁举出的例子不符合猜想的？

（学生举出了三位数乘法和小数乘法的例子，发现自己任意举出的例子都是符合猜想的，其后在与同学交流中并没有发现反例，再次验证了猜想。）

4.引发思考

如果：○×☆=120

那么：○×（☆×3）=（○×2）×☆=

（○×10）×（☆×10）=（○×2）×（☆×3）=

○×（☆÷3）=

（○÷2）×（☆÷3）=（○÷2）×（☆×5）=

师：积还会怎么变化？有规律吗？会有怎样的规律？请同学们课后运用今天学到的方法进行验证。

本课设计，重在让学生在教师的引导下探索积的变化规律，经历一次完整的“猜想规律——举例验证——运用规律”数学活动过程，体会“不完全归纳”的数学思想方法。如何让学生学会运用经验去发现新的规律，并且在运用中积累新的经验是这节课我们要达成的更高目标——成为“用计算器探索商不变的规律”的经验基础。

第二课时“用计算器探索商不变的规律”片断：

1.经验迁移

师：上节课我们借助计算器探索了乘法运算中积的变化规律，一起来看上一节课的课件。（课件回放）谁来说说我们是如何研究的？

生1：观察例题，我们发现一个因数不变，另一个因数变化，积也发生了变化。（板书：猜想规律）

生2：然后举例验证猜想。（板书：举例验证）

师：是不是举了一个例子？还举了怎样的例子？这些例子中有没有不符合这个猜想的？（板书：大量，特殊，没有反例）

师：经历了这样一个探索的过程，最后我们得到了积的变化规律，并且运用规律来解决了一些实际问题。课的最后，老师给出一组拓展题，同学们可以在课后进一步探究乘法中还有没有别的变化规律。那么，除法中，被除数和除数同时除或乘相同的数，商会怎样呢？有没有规律呢？今天我们继续用上节课的方法来研究除法运算中的规律。

2.自由经历探索过程

（1）4人小组讨论，提出猜想；

（2）自由举例验证猜想；

（3）得出结论；

（4）全班交流汇报。（关注特殊数字的例子，如“零”等）

数学课程标准指出：“课程内容既要反映社会的需要、数学的特点，也要符合学生的认知规律。它不仅包括数学的结果，也包括数学结果的形成过程和数学思想方法。”据此分析，第一课时，更强调让学生经历数学活动的全过程，在这个过程中，让学生体验一种由特殊到一般的推理方法，初步体会由具体到抽象、由特殊到一般的归纳思想。因为小学生知识经验和认知水平有限，第一课时教师以引导为主，通过一个特殊的例子，引发猜想，通过列举大量的例子来证明猜想，其间关注了特殊的数字，关注了有没有反例，在得到结论后让学生利用结论去解决实际问题，从而经历用不完全归纳法发现规律的过程。第二课时则通过回忆激活学生在第一课时积累的学习经验。放手让学生用眼观察，比较相关算式的内在联系；让学生动脑去想，抽象出“不变”的特点；让学生动口去说，概括出商不变的规律；让学生在多种感官的协同活动中主动获取知识，

学生学习数学需要有一个意义建构的过程，这一过程以原有经验为基础，并且所建构的意义最终以经验的形态储存在学生的大脑中。如果第二课时与第一课时一样，教师扶着学生一步步前行，这种单调的重复就不具有递进性，就失去了让学生丰富、内化经验的好时机。因此，前后两节课的教学，从第一节课教师的半扶半放，引领学生探索发现规律，到第二节课教师的完全放开，让学生自主探究，目的在于，通过这种递进式的教学，充分激发学生的探究潜能，激活学生业已形成的知识经验，让学生再一次参与知识的建构过程。学生在探究中多次尝试、思考、追问，体会越来越深，所积累的活动经验在内化的同时更科学、更丰富，在主动的探索过程中形成对数学知识的深刻理解并感悟数学思想方法。

对于数学学科而言，学生学会学习需要掌握基本的数学学习技能，更需要掌握观察、猜想、验证、推理等数学的思维方法，实现由已知到未知，由具体到抽象，由感性到理性，由现象到本质的跨越，逐步由“学会”到“会学”。可见，数学教学以学生为主体，引导学生经历学习过程、积累数学活动经验是非常必要的。因此，在数学教学中，教师应选择合适的内容，安排合理的时机，引导学生自主探索学习数学。

（责编金铃）

G623.5

A

1007-9068（2016）20-005