以“导学案”为依托，培养学生发现和提出问题的能力——以苏教版六年级“图形的放大和缩小”一课教学为例

江苏扬州市梅岭小学西区校（225002）　殷丽萍



以“导学案”为依托，培养学生发现和提出问题的能力
——以苏教版六年级“图形的放大和缩小”一课教学为例

江苏扬州市梅岭小学西区校（225002）殷丽萍

“疑”能产生动力，孕育着发现。发现和提出问题的能力关乎学生数学学习品质的提升，关乎他们创新意识和实践能力的发展，甚至关乎学生的未来。因此，教师应改善学生的学习方式，以“导学案”为依托，培养学生发现和提出问题的能力，让学生受益终身。

导学案发现问题提出问题综合素养能力图形放大缩小

教学重点：

初步理解图形的放大和缩小，能利用方格纸按一定的比例将图形放大或缩小。

教学难点：

使学生在观察、比较、思考和交流等活动中，感受图形的放大、缩小，初步体会图形的相似，进一步发展空间观念。

教学目标：

1.使学生初步理解图形的放大与缩小，能利用方格纸按一定的比例将简单图形放大或缩小，初步体会图形的相似。

2.通过教学，培养学生的空间观念和抽象、概括等思维能力。

教学预设：

师：同学们，我们已经学习了图形的平移和旋转等知识，今天我们继续学习图形的变换。请同学们按照导学案的要求进行探究，你们一定会大有收获！

一、自主研究

师（出示下图）：拖动电脑鼠标可以将图①分别放大成图②、图③、图④，你认为图（）是图①数学意义上放大后得到的图形？同时说明自己的理由。

……

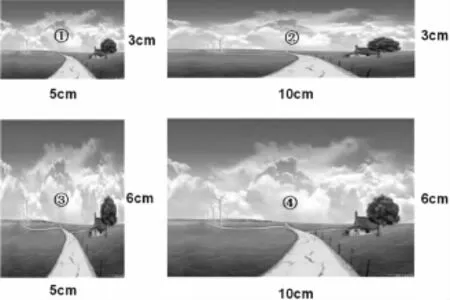
师（出示图⑤）：图⑤是图①放大后得到的图形吗？为什么？

……

师：从你认为怎样才算是数学意义上的放大？数学意义上的放大与生活中的拉伸有何区别？

……

师：图①到图④，放大后长方形的长与原来长方形的长有什么关系？宽呢？如果用一个比来表示这种放大的规律，是（）∶（）。（生答略）

师：请自学课本第38页例1，对解决以上问题也许会大有帮助。（生自学）

师：你如何理解“把原来的长方形按2∶1的比放大”？（生答略）

师：如果把例1中原来的长方形按1∶2缩小，长和宽应是原来的几分之几？各是多少厘米？

……

二、自主巩固

师：请同学们自主完成课本第39页例2、试一试、练一练以及练习九的第1题和第2题。

三、自主反思

师：通过对“图形的放大和缩小”的自学，你有什么收获？还有什么疑问？

……

教学实录：

一、揭示课题，明确目标

师：今天我们学习的内容是“图形的放大和缩小”，从学习目标来看，通过本节课的学习，我们要达到什么样的要求？（生答略）

师：在学习过程中，你有什么想法和疑问？（课前师对学生的学案进行整理和分析，选择几个问题在课上指名学生回答，师做记录，如下）

生1：两个图形长的比和宽的比不一样，是不是放大或缩小？

生2：怎样判断一个比是把图形放大还是缩小？

生3：为什么在说按“几比几”的比放大或缩小时，比的前、后项的顺序与图形的顺序相反？

生4：书上的练习中长方形的长和宽都放大了1.5倍，是按几比几放大的？

生5：怎样把梯形、平行四边形放大或缩小？

……

师：同学们提出的问题都很有价值，下面我们就带着这些问题进行研究。

二、自主探究，交流展示

1.初步认识图形放大的含义。

师：按照平时的想法，上述图②、图③、图④都是把图①进行放大，但只有一幅图符合数学意义上的放大，你认为是哪一幅图？为什么？

生6：我认为是图④，因为这幅图的长和宽都放大了，看起来比较协调，而图②只是把长拉长了，图③只拉长了宽，所以图②和图③不符合数学意义上的放大。

师：图⑤是图①放大后的图形吗？为什么？

生7：不是。和图①相比，虽然图⑤的长和宽都进行了放大，但放大的倍数不一样，所以看起来长方形的形状发生了变化。

师：你认为怎样才算是数学意义上的放大？数学意义上的放大与生活中的拉伸有何区别？

生8：数学意义上的放大应该是把图形的每条边都放大相同的倍数；生活中的拉伸只是拉长图形的某一条边，或是图形中每条边放大的倍数不同。

生9：数学意义上的放大应该是形状不变，而拉伸会使图形发生变形，看起来不匀称。

生10：数学意义上的放大应是按比例放大，而拉伸不是。

……

2.建立概念。

（1）理解图形的放大。

师：从图①到图④，放大后长方形的长与原来长方形的长有什么关系？宽呢？

生11：放大后长方形的长是原来长方形的2倍，宽也是原来的2倍。

生12：放大后长方形的长与原来长方形的长的比是2∶1，宽的比也是2∶1。

师：谁能把他们的话合起来说？

生13：放大后的长方形的长和宽都是原来的2倍。

生14：放大后的长方形的长和宽与原来长方形的长和宽的比都是2∶1。

师：书上是如何概括的？

生（齐读）：把长方形的每条边放大到原来的2倍，放大后的长方形与原来长方形对应边长的比是2∶1。

师：这里“对应边长的比”怎么理解？

生15：就是两个长方形的长比长，宽比宽。

师：用一个比来表示这种变化的规律，你觉得是几比几？

生（齐答）：2∶1。

师：同学们原来都是这么想的吗？还是自学以后的答案？

生16：我原本认为是1∶2，因为我想的是从原来到现在，原来是1份，现在是2份，所以是1∶2。

生17：我原来的答案也不是2∶1，我想的是1∶4，因为原来长方形的面积是15cm2，现在的面积是60cm2，所以是1∶4。

生18：我想的是4∶1，因为我也是想到了长方形面积的比。

师：大家说的都很有道理。那么，数学书上的规定与大家所想的有何不同？

生19：书上是放大后的长方形与原来长方形的比。

生20：我来补充。书上是现在和原来对应边长的比，而不是面积的比。

师：对应边长的比和面积的比相同吗？

生：不同。

（2）认识图形的缩小。（略）

（3）交流练习九的第1题。（重点交流图①到图⑤是按几比几放大的）

（4）在方格纸上按一定的比画出放大或缩小后的图形。（略）

（5）交流汇报试一试、练一练以及练习九的第2题。

三、释疑解惑，合作讨论

师：课前大家提出了一些问题，通过交流，已经解决了哪些问题？还有哪些问题没有解决？我们来继续讨论。

生21：“长方形的长和宽都放大了1.5倍”，我知道这里是按3∶2的比放大的，是放大后的长方形与原来长方形长的比和宽的比。

生22：我来回答“为什么在说几比几放大或缩小的时候，与图形的顺序是相反”的问题。自学的时候，我也不太明白，后来我上网查，网上说“这个比是新画的图形与原来图形对应边长的比，后面我们要学一个知识，叫做比例尺，比例尺是图上距离和实际距离的比，和今天的这个比形成对应关系”。

师：真了不起，还会求助于网络，你帮大家解决了一个大难题！还有其他同学要发表意见吗？

生23：我发现比的前项比后项大，表示放大；前项比后项小，表示缩小。

生24：我是看比值的，如2∶1的比值是2，表示放大；1∶2的比值是1/2，就表示缩小。

师：比值多大时，表示放大？比值多大时，又表示缩小呢？

生25：比值比1大时，表示放大；比1小时，表示缩小。

师：还有一个问题。如何把梯形或平行四边形等图形放大或缩小？你能举个例子吗？

……

四、课堂总结，反思提升（略）

五、修改学案，拓展延伸（略）

……

思考：

问题是思维的起点，是创新的源泉。《数学课程标准》明确指出了培养学生创新意识的途径：“学生自己发现和提出问题是创新的基础。”爱因斯坦也曾经说过：“提出一个问题比解决一个问题更为重要，因为解决问题也许是一个数学上或实验上的技能而已，而提出新的问题、新的可能性，从新的角度去看旧的问题，却需要创造性的想象力，而且标志着科学的真正进步。”那么，在数学教学过程中，如何培养学生主动发现和提出问题的能力呢？这就需要我们教师改变原有的教学方式，将学生的学习变“被动”为“主动”。而“学案导学”中“先学后教，师生互动”的教学模式是一个有效的载体，主要体现在以下几个方面。

1.充足的思考时间，是学生发现和提出问题的基础。

“学案导学”与传统教学的最大区别在于将学生的学习进行前置，且课前的先学过程给予了学生充足的思考时间与空间。有思考才会有疑问，学生带着问题进入课堂，更容易激活学生的思维，调动学生的学习积极性。学生对知识的理解越深刻，就越容易发现新的问题，这样提出的问题才会更有意义、更具价值。如上述教学中，学生发现和提出的问题都是他们经历充分思考后的真实思维显现，是带有个性思考的发现。同时，“学案导学”能暴露出学生思维过程中的困难、障碍、疑问、错误，利于教师调整教学过程。如上述教学中，有学生认为面积放大了4倍，所以图形是按1∶4的比例放大的。这说明只有学生已有的知识经验与新知产生矛盾时，才会引发新的思考和新的问题。数学学习离不开思考，学生只有经历充分的思考后，才能形成自己的想法和见解。

2.厚实的知识储备，是学生发现和提出问题的关键。

“发现和提出问题的过程是建立在对事物或现象进行观察、比较基础上的，需要分析、综合考察事物或现象的各种本质属性及内在联系，从新的角度，发挥想象，提出有实际意义的、有价值的问题。”这对于小学生而言，不是简单的事情。学生只有具备一定的知识储备，这样学习新知时，已有的知识储备才可能与新知相互作用，形成认知冲突，进而产生困惑、疑问。所以，有足够的知识储备是学生发现和提出问题的关键。如上述教学中，教师首先调动学生已有的知识经验，通过对问题“哪一幅图才是数学意义上的放大”的正、反例辨析，使学生对数学中的放大有一个初步的感知，接着以“长和宽放大的倍数不同”的反例，帮助学生进一步完善对概念内涵的认识。然后教师引导学生辨析数学中的放大与生活中的拉伸的不同点，使学生完成对概念的定性把握，帮助学生逐步建构新知。当学生利用已有的知识经验解决不了新的问题时，或旧知识与新知识存在“脱节”的情况，需要学生通过各种途径（如查阅资料、网上搜索、请教家长或同学等）去弥补知识的漏洞，以寻求知识的重组。如教师提出“在描述是按几比几放大或缩小时，为什么是变化后与原来的比”的问题后，学生想到了上网查阅的方法，这样既满足了自己强烈的好奇心和求知欲，又找到了知识的延伸点，完善了自身的认知结构，为后续学习奠定基础。

3.和谐的学习氛围，是学生发现和提出问题的保障。

心理学研究表明：“一个人的创新思维只有在他感觉到心理安全和自由的条件下，才能获得最大限度的表现和发展。”所谓心理安全，是指不需要有戒备心，不会受到苛求和责备。所谓心理自由，是在思考问题时没有过多的束缚，能够比较自由地思考和表达。因此，在数学课堂中，教师要想方设法创建宽松、和谐的教学环境。首先，“学案导学，师生互动”的教学模式既能营造轻松、活泼的课堂气氛，让课堂成为学生展示自我的舞台，又增强了师生、生生之间的互动交流，使每个学生都敢说、敢想、敢问、敢于探索及张扬个性，生成精彩的课堂教学。其次，课上及时的反馈和展示，给予了学生表现的机会，激发了学生的表现欲，既能展示学生的预习成果，又能呈现学生自己的想法和疑问。此外，在“学案导学”中，教师要鼓励学生提出自己的想法和问题，然后围绕学生学习中产生的问题去展开教学，凸显学生的学习主体性，并把提出问题和解决问题的权利交给学生，让学生自主去发现、去研究。宽松、和谐的学习环境，能保持学生继续主动参与教学过程的信心和热情，培养了他们良好的问题意识。

4.有效的学习方式，是学生发现和提出问题的源泉。

教育心理学家布鲁纳的“发现学习”理论强调：“学生的学习应是主动发现的过程，而不是被动地接受知识。”“先学后教”强调在“导学案”的指引下，学生对知识的自主建构，从真正意义上培养学生的自主学习能力，使学生从“学会”走向“会学”。数学学习的过程，是“问题的提出——问题的解决——新问题的提出”的过程。“学起于思，思源于疑。”学生长期处于这样“以问启思，以问导学”的学习机制下，有效地培养了他们的问题意识。同时，教师课前对学生的学案进行整理与分析，精选出有价值的问题供学生课上探究、讨论和交流，日积月累，使学生积累了学习的经验，能够辨别出什么样的问题有价值、什么样的问题没有意义，对学习有促进和发展的作用，从根本上提高了学生发现和提出问题的能力。

总之，“疑”能产生动力，孕育着发现。发现和提出问题的能力关乎学生数学学习品质的提升，关乎学生创新意识和实践能力的发展，甚至关乎学生的未来。因此，课堂教学中，教师要改善学生的学习方式，以“导学案”为依托，培养学生发现和提出问题的能力，使学生受益终身。

（责编杜华）

G623.5

A

1007-9068（2016）20-017