高中数学课程建设的构想与实践

□ 海南省海口市第一中学 黄耀国

高中数学课程建设的构想与实践

□ 海南省海口市第一中学 黄耀国

在长期的实践中，我校数学组的课程体系雏形初现，数学组坚持“在统计中规划策略，在规划中提高效率，在研究中把握方向，在整编中获得发展”的指导思想，贯彻执行“资料自编，滚动复习，统计诊断，三个凡是”工作章程，以课程的校本化为载体，逐步完善海口一中数学配套资料校本化和命题研究的校本化工作.并形成其特有的课程基地建设构想与实践操作。

一、关于高中数学课程建设的构想

经过多年实践，海口市第一中学数学校本课程开发活动有课程选择、课程改编、课程整合、课程补充和课程创新等活动。在新课程改革的背景下，数学往往以问题为中心，将基本数学知识、基本的数学思想和方法融为一体，突出了数学思想方法，体现了数学的思维价值。以数学问题作为课程与教学内容反映了在解决数学问题过程中数学的重要规律和方法，它在人的数学思维一系列过程（包括推理、类比、归纳、运算等）与人类的思维发展的目标之间架起了一座桥梁。关于数学问题的价值就在于数学问题作为教学内容在教学中起到无可替代的导向性发挥着重要作用。数学问题相应地就成为了最理想的思维训练的素材，是数学知识综合的载体，是学生主动探究的支点。

二、高中数学课程建设的操作流程

美国课程理论学者肖特（Short.E.C）认为：在实际的教育场所发生的并可望能够使教师们积极地参与并卷入到广泛的相互作用和课程决策之中的一种课程开发策略。根据肖特的理论，我们将其操作可以构建为左边的示意图（见左图）.

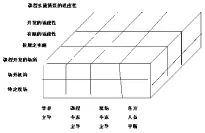
围绕课程建设肖特的理论，结合实践，我们构建出自己的课程建设操作流程：

三、高中数学课程建设实践

1.利用数学课程建设的历程提升数学教师专业。关于数学课程建设研究我们主要经历了初始阶段：发现课程问题、形成校本课题；发展阶段：研究课程建设课题或专题、形成校本科研成果；实践阶段：进行课程科研成果的鉴定；推广阶段：推广使用数学课程建设科研成果，其发展历程如图1：

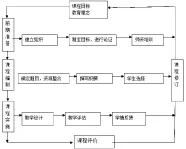
2.利用数学课程建设的历程促进教学有效性。“问题是数学的心脏”，著名数学教育家波利亚在《数学的发现》一书中曾给出问题明确含义，并从数学角度对问题做了分类。他指出：所谓有问题，指的是有意识地寻求某一适当的行动，以便达到一个被清楚地意识到但又不能立即达到的目的。从问题特点的角度，我国学者曾提出了如下观点：“问题的呈现应该激起学生的思考”、“问题要有一定的现实性包括内容的现实性和问题的现实性两方面”、“问题要有一定的趣味性”，这种对问题特征的描述为大家广为接受。我国的张奠宙、刘鸿坤教授在他们的《数学教育学》里的“数学教育中的问题解决”中，对什么是问题及问题与习题的区别做了很好的探讨，提出了“问题是一种情境状态”、“问题解决中的问题与习题、练习不同”、“问题是相对的”等观点。比如，笔者对以下问题的设计：

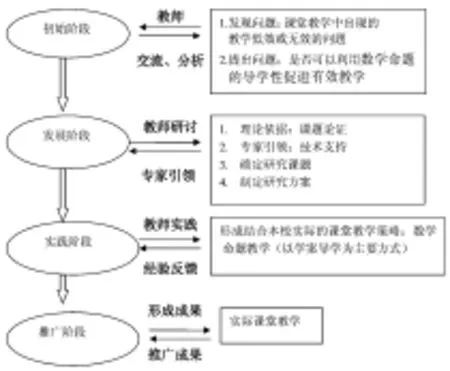
图1

例：某市为了对学生的数理（数学与物理）学习能力进行分析，从10000名学生中随机抽出100位学生的数理综合学习能力等级分数（6分制）作为样本，分数频数分布如下表：

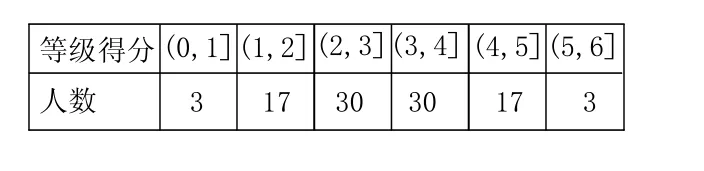
（0，1］等级得分人数（1，2］（2，3］（3，4］（4，5］（5，6］3　17　30　30　17　3

（1）如果以能力等级分数大于4分作为良好的标准，从样本中任意抽取2名学生，求恰有1名学生为良好的概率；

（2）统计方法中，同一组数据常用该组区间的中点值（例如区间的中点值为1.5）作为代表：

①据此，计算这100名学生数理学习能力等级分数的期望及标准差（精确到0.1）。

② 若总体服从正态分布，以样本估计总体，估计该市这10000名学生中数理学习能力等级在范围内的人数。

（3）从这10000名学生中任意抽取5名同学，他们数学与物理单科学习能力等级分数如下表：

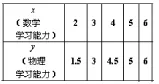
①请画出上表数据的散点图；

②请根据上表提供的数据。

用最小二乘法求出y关于x的线性回归方程^y=bx+a

问题推动探究：在学生的学习中，我们总是将概率统计人为地分为不相融合的两个知识内容，这其实是一大误解。以概率的概念而言，在中学教材中，其首先是以频率呈现，而频率是以统计为基础的。这充分说明，统计与概率其本身就需要融为一体。上面问题的呈现，就是要学生将统计与概率作为一个整体来探究。不仅如此，问题还融合了课改区的“研究性学习”和“综合实践模块”的背景，对这类有一定实践性试题，让学生从问题中也体会到概率统计作为一个整体是如何解决现实生活中的一些问题，使得学生在学科整体意识上进行研究，这对概率和统计的应用将会产生深远的影响。那么，概率与统计是通过什么形式融合为一体的呢？学生可以通过探究上面的问题认真体会。实际上，在概率与统计中，“平均数、方差、标准差”等基本概念就是他们联系的纽带。下面，还是让我们和学生一起来探究本题的解法：解：（1）样本中，学生为良好的人数为20人.故从样本中任意抽取2名学生，则仅有1名学生为良好的概率为

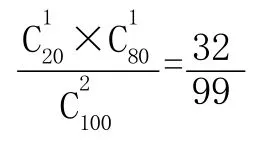
（2）①总体数据的期望约为：μ=0.5×0.03+1.5× 0.17+2.5×0.30+3.5×0.30+4.5×0.17+5.5×0.03=3.0

标准差σ=

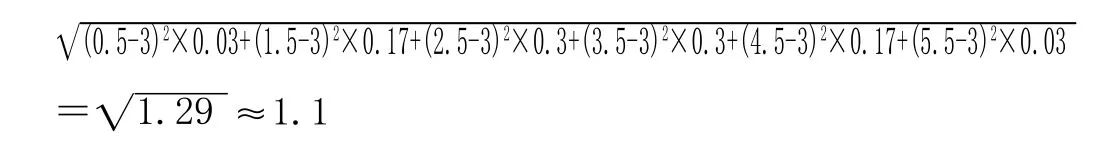
②由于μ=3，σ≈1.1

当x∈=（1.9，4.1）时，即x∈（μ-σ，μ+σ）故数学学习能力等级分数在（1.9，4.1）范围中的概率0.6826.数学学习能力等级在（1.9，4.1）范围中的学生的人数约为6826人.

（3）

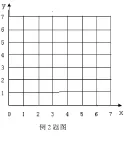
①数据的散点图如下图：

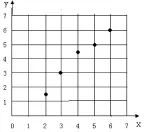
②设线性回归方程为^y=bx+a，则

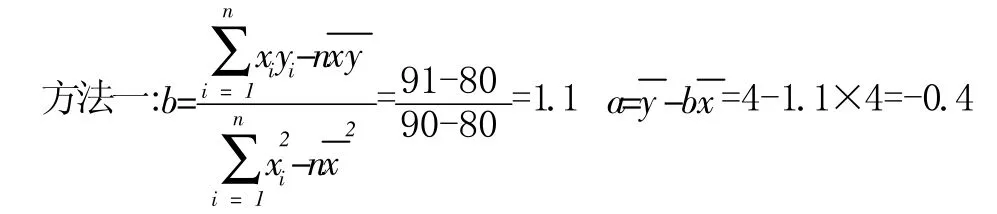
故回归直线方程为y=1.1x-0.4

方法二：

f（a，b）=（2b+a-1.5）2+（3b+a-3）2+（4b+a-3.5）2+（5b+a-5）2+（6b+a-6）2

f（a，b）取得最小值10b2-22b+12.5

即，∴b=1.1，a=-0.4时f（a，b）取得最小值；

所以线性回归方程为y=1.1x-0.4

3.利用数学课程建设历程促进学生主动探究意识。我校教师在怎样实现教与学的统一的问题的不断探索过程中逐渐达成共识，采用以数学命题为导向性的教学方法——资料整编。

充分利用数学命题的导向性，以典型例题明确考点，注重解题方法的渗透，学生根据整编资料中的各环节学习最终要达到理解和掌握数列求和的常见的方法，运用所学的知识来解决问题，同时在应用之中达到巩固和提高。题不在多而在于精，突出重点知识，也具有诊断功能，用于检查学生掌握这些知识的程度。活动如下图所示：

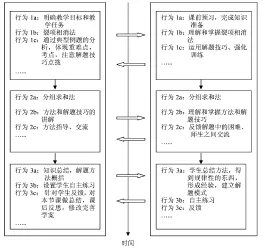
问题要作为教学内容或者是学生的学习内容，重要的是它起到的是一种导学性。在课堂教学中以问题作为知识的载体，通过其导向性促进学生的探究意识，有效地建构知识体系，实现教师的有效地教和学生有效地学的统一。学习的目的是通过经验的获得来引起行为变化。因此，课程意识在课程建设中有重要的建构意义。

［1］G·波利亚.怎样解题［M］.北京：科学出版社，1982.

［2］数学课程标准研制组.数学课程标准解读［S］.南京：江苏教育出版社，2004.

［3］王梓坤.今日数学及其应用，面向21世纪的数学教育--数学家论数学教育［M］.南京：江苏教育出版社，1994.

黄耀国，华中师范大学硕士学位，现任海口一中数学教研组长；全国首届教育改革创新优秀教师，海南省数学学科带头人，海南省先进工作者，数学奥林匹克一级教练员，海南省数学竞赛优秀辅导教师，中国数学教育学会优秀实验教师，海南省基础教育改革先进个人，海南省先进实验教师，“十五”规划课题先进实验教师）