声结构耦合系统双材料模型的拓扑优化设计

商林源, 赵国忠， 陈　刚

(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连　116024;2.上海电气电站设备公司 上海汽轮机厂,上海　200240)



声结构耦合系统双材料模型的拓扑优化设计

商林源1, 赵国忠1， 陈刚2

(1.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连116024;2.上海电气电站设备公司 上海汽轮机厂,上海200240)

基于微结构设计域法，并结合伴随法与放松形式准则法，研究了针对声结构耦合系统的双材料拓扑优化方法。提出并详细地推导了声压级关于拓扑变量的伴随灵敏度分析公式。推导了一种放松形式的最优准则法，并应用到声结构耦合问题的优化求解中。数值算例证明了在求解声结构耦合问题中，伴随灵敏度分析方法具有高精度，高效率的特点；放松形式的最优准则法具有收敛快速，迭代稳定的优点。数值结果说明文中提出的拓扑优化方法能有效降低结构内部的噪声，验证了方法的正确性。

声结构耦合系统;拓扑优化;伴随法;最优准则;双材料模型

随着人们环境保护意识的提高，噪声污染问题越来越受到社会的关注。企业希望在产品设计阶段就能预知其噪声指标，因此数值方法对于预估以及优化产品的声学性能具有重要的实际意义。

拓扑优化方法作为一种新的结构优化方法得到了快速发展，并广泛应用在工程中。BENDSØE等[1]提出了拓扑优化的均匀化方法。SIGMUND[2]开发了经典的99行拓扑优化程序，在拓扑优化领域被广泛的学习。ANDREASSEN等[3]对动力载荷下的结构拓扑优化设计进行了研究。JOG[5]研究了周期载荷作用下的最小动柔度和最小频率响应的拓扑优化方法。GUO等[6]提出了一种解决应力和局部屈曲约束下的桁架结构拓扑优化奇异最优解的方法。近年来，拓扑优化在声学领域中也开始应用，LEE等[7]研究使用遗传算法的薄结构声学辐射和散射拓扑优化问题。KANG等[8]研究通过优化壳结构阻尼层降低声辐射的拓扑优化方法。DU等[9]以最大结构特征频率和最小动柔度为优化目标，采用拓扑优化方法降低结构声辐射。AKL等[10]使用移动渐近线法对声腔与板结构耦合的拓扑优化方法进行了研究，并通过实验加以验证。SHU等[11]提出基于水平集法的声结构耦合拓扑优化方法。LIU等[12]研究了随机激励下声辐射的设计优化方法。YANG等[13]对声辐射的微结构拓扑优化设计进行了研究。NIU等[14]发展了对层合板振动噪声的拓扑优化方法。刘海等[15]采用拓扑优化方法设计加强筋布局降低结构辐射声功率。

由于传统的拓扑优化过程会产生结构的镂空，不能保证结构的密封性，因此内声场的拓扑优化方法需要对传统方法进行改进，而相关研究工作也较少。文献[16]使用了一种优化刚度层的拓扑优化方法，避免了结构产生孔洞。本文基于微结构设计域法，提出了声结构耦合系统的双材料拓扑优化模型。考虑到拓扑优化设计变量数目大，有限差分法不适合求解大计算量问题，本文提出了针对声结构耦合问题的伴随灵敏度方法，并推导了关于声压级灵敏度分析公式。传统的最优准则法[17]具有计算效率高的特点，被广泛的应用在结构优化求解中，而在声学优化中应用较少。考虑到声结构耦合问题计算量较大，本文首次将优化准则法应用到了声结构耦合系统的优化中，由于准则法中成本函数要求具有非负性，为了避免在声结构耦合优化中成本函数出现负值，采用了一种放松形式的最优准则法。

1　声结构耦合系统有限元方程

声结构耦合系统有限元方程为[18]：

(1)

式中:ρ0为声场介质密度，Ma和Ka分别为声场的质量矩阵和刚度矩阵；Ms和Ks分别为结构的质量矩阵和刚度矩阵；fs为作用在结构上的外部力；其中Mas和Ksa为声场结构耦合矩阵，满足Ksa=-MasT；us和p分别为系统位移和声压。

若外力为简谐激励 Fseiωt， 则系统位移和声压分别为为Useiωt和Peiωt，因此式(1)可表示成如下形式：

ZU=F

(2)

式中:

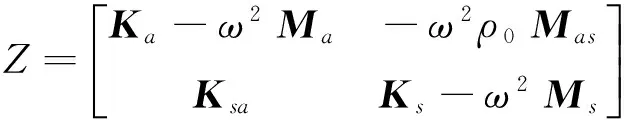
(3)

Z为耦合系统的阻抗矩阵；U为耦合系统响应幅值向量，包括声压幅值向量P和位移幅值向量Us；F为耦合系统的外力幅值向量，Fs为作用在结构上的外力幅值向量；ω为激励的角频率。

2　声结构耦合系统的拓扑优化模型

传统的拓扑优化方法是在给定的设计空间中寻找已知某种材料最优分布使得结构获得刚度最大，柔度或者响应最小的结构优化方法，优化过程包括对优化目标的结构响应分析、灵敏度分析和求解极值问题三个步骤，通过反复迭代直至收敛，结构中出现孔洞，得到的最优材料分布使得目标函数到达极小值。

对于封闭的声结构耦合系统，由于要求结构必须是封闭的，若采用单一材料的拓扑优化模型，则会产生结构的镂空，不能保持声场封闭性。因此，本文采用了文献[19]提出的MBDDM (Microstructure-Based Design Domain Method)，将该方法拓展到声结构耦合问题中，得到由基材料和刚度材料构成的双材料拓扑模型，如图1所示。

图1　拓扑优化双材料模型Fig.1 Bi-material model of topology optimization

双材料模型的力学性质可描述如下：

(4)

(5)

ρ(i)=ρ1c(i)+ρ0(1-c(i))

(6)

其中

(7)

式中：κ，μ和ρ分别为材料的体积模量，剪切模量和密度；ν为泊松比；上标i为单元编号；下标0和1分别为基材料和刚度材料；c为刚度材料的相对体积密度。

在声结构耦合系统的优化设计中，优化目标和约束函数包括：声场某点声压级、空间平均的声压级、频带平均的声压级以及结构设计重量等，声压级是最直接的噪声指标，作为目标函数，结构的重量作为约束函数。根据声压级的定义得到：

SPLj=10lg(Pj/P0)2

(8)

(9)

式中:Pj为第j号声场节点的声压，P0为参考声压，一般取2.00×10-5Pa，SPLj为声场某点的声压级；n为选取的声场节点数，SPLn为选取的n个节点的平均声压级。当激励频率是分布于ω0到ω1的频带内，那么耦合系统在带宽为 Δω频带上的平均声压级为如下形式：

SPLΔω=

(10)

因此，对于声结构耦合系统拓扑优化问题，可以表示成：

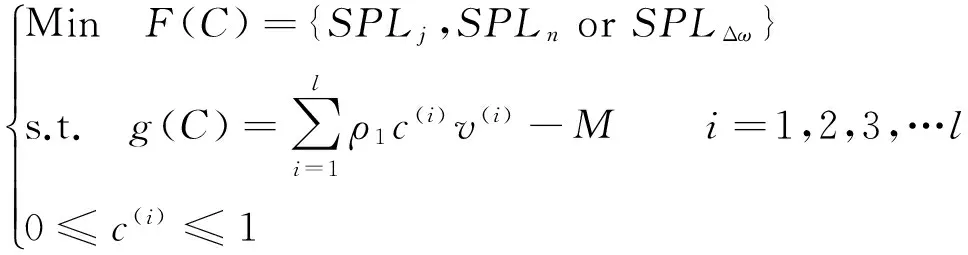
式中：F(C)为目标函数，g(C)为约束函数，M为刚度材料总重量，v(i)为i号单元体积，l为设计变量个数。

3　声结构耦合系统的灵敏度分析

灵敏度分析的目的是确定系统响应对设计参数的改变的敏感程度，作为基于梯度的优化求解的关键，灵敏度计算精度直接影响优化求解的正确性，而求解灵敏度的效率也直接决定了优化的效率，本文采用了伴随法求解关于声压级的灵敏度，首先对式(2)两边对设计变量求导得到耦合系统稳态响应灵敏度：

(12)

其中，

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

由于拓扑优化中设计变量数目多，若采用直接法求灵敏度计算量过大。取向量ξjT={0,0,…,1,0,…}T，其中只在作为优化目标的第j号元素等于1，其他元素均取0。因此采用伴随法求解声压灵敏度：

(24)

将式(12)代入式(24)，得到

(25)

Y称为伴随向量。

YjT=ξjTZ-1

(26)

最终求出声压级的灵敏度计算公式：

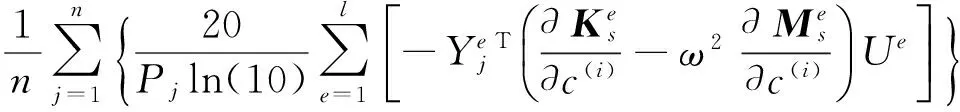
(29)

4　声结构耦合系统的优化求解算法

本文采用放松形式的最优准则法[20](OC)进行优化求解。最优准则法以最优解满足库恩塔克条件作为结构最优准则，设计变量的更新根据该准则构造的显式的迭代公式实现，公式中引入经验系数调整优化的收敛性和稳定性。最优准则法迭代公式简单，迭代次数不依赖设计变量数，具有较高的优化效率。式(11)的库恩塔克条件可以写成：

(30)

式中:λ为拉格朗日乘子。此时采用放松方法，在式(30)中引入放松因子ψ，得到：

cF(C)+(λ*-ψ)cg(C)=0

(31)

式中：λ*为考虑放松因子的拉格拉日乘子，满足λ*=λ+ψ。放松因子ψ满足下式：

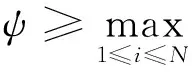
(32)

根据式(31),得到成本函数Bk：

(33)

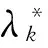
ck+1=

式中：ck为第k步迭代时的设计变量值，调试参数η=0.5，移动极限ζ=0.1。当Bk=1，设计变量获得最优解；当Bk>0，增大设计变量；当Bk<1，减少设计变量。

5　数值算例

如图2所示，一方型封闭空腔长0.7 m，宽0.7 m，高0.4 m。 结构顶面采用厚度4 mm的弹性板，并作为拓扑优化设计域， 其他面均为刚性面。 对设计域采用双材料模型，其中基材料密度和弹性模量分别为1 000 kg/m3和2 GPa，泊松比0.3，刚度材料密度和弹性模量分别为1 000 kg/m3和3 GPa。初始刚度材料相对体积密度为0.5。结构总重量为1.96 kg，其中刚度材料总重0.98 kg，并作为优化的重量约束。腔体内空气密度1.21 kg/m3，声速为340 m/s。对于声场和结构分别采用8节点声场单元和4节点壳单元。

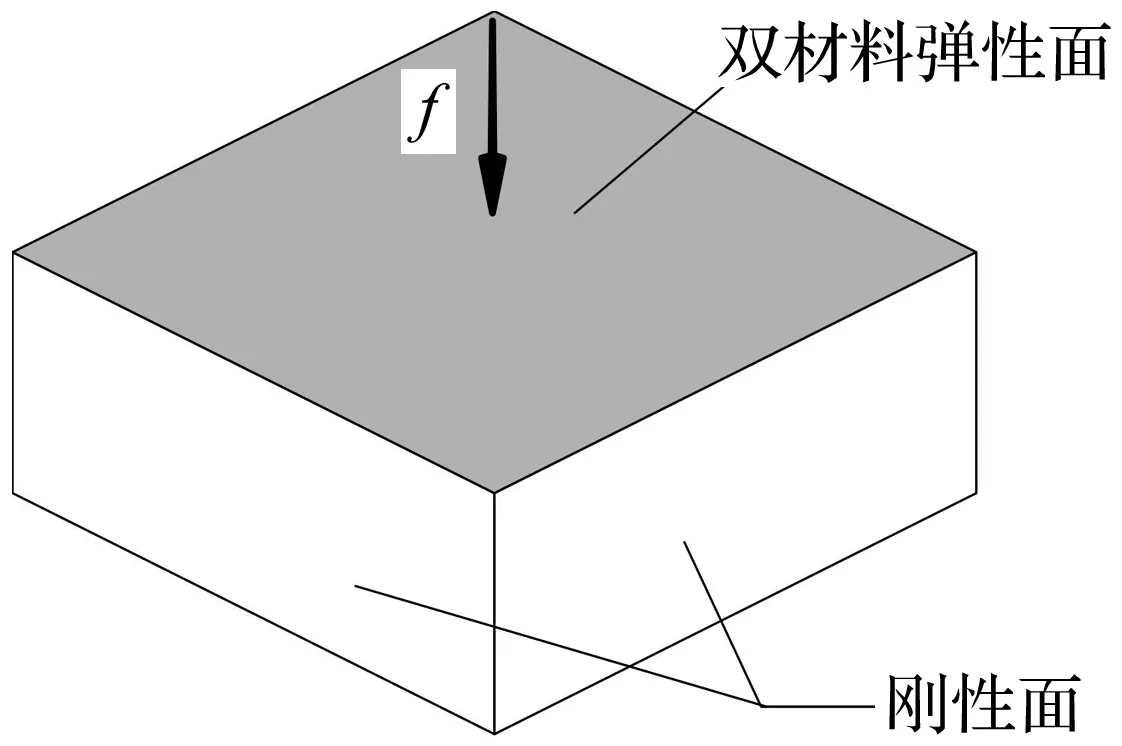
图2　声结构耦合系统模型Fig.2 Model of acoustic-structural coupled systems

5.1最大声压级的拓扑优化

顶板中心处作用幅值0.1 N，频率45 Hz的简谐力，方向沿着顶面法向。如图3(a)所示，最大声压级出现在声腔顶面的角节点，板中心声压级最小。右上角处的最大声压级选为目标函数，约束函数为刚度材料重量。采用伴随法计算灵敏度，计算结果如图4所示，横向网格数和纵向网格数均为70个，灵敏度总数为4 900个，白色表示灵敏度是正值，黑色和灰色代表灵敏度是负值，在正灵敏度位置减少刚度材料或在负灵敏度位置增加刚度材料均可以降低最大声压级。采用有限差分法(FDM)验证伴随法灵敏度分析的计算精度，图5给出了两种方法计算结果的相对误差，最大相对误差小于3%，验证了伴随法求解声压级灵敏度的精确性，采用伴随法CPU用时0.706 1 s，差分法用时1.107 8×104s，可见差分法不适用于声结构耦合问题的灵敏度分析，伴随法的高效率凸显。

图3　优化前后声压级分布Fig.3 Contour of SPL before and after optimization

图4　伴随灵敏度分析结果Fig.4 Results of adjoint sensitivity analysis

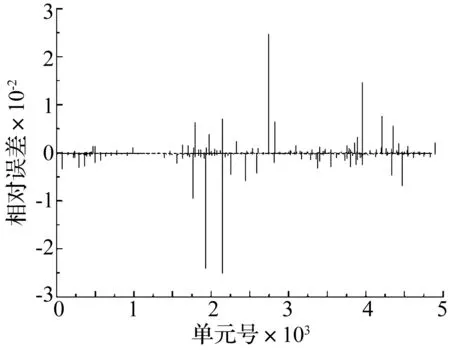
图5　伴随法和差分法求灵敏度的相对误差Fig.5 Relative errors of sensitivities between adjoint method and FDM

采用OC方法求解目标函数最优值，经过37步迭代，目标函数从初始的96.49 dB收敛到94.00 dB，降低了2.49 dB，CPU用时121.351 7 s。为了验证放松形式的OC方法在处理声结构耦合问题的精度和效率，采用移动渐近线法(MMA)作对比，使用MMA目标函数经过50次迭代收敛到94.03 dB，CPU用时289.581 1 s。若图6所示，用MMA求解目标值时，在迭代的前四步下降的速度明显快于使用OC，但在第五步进入收敛阶段后迭代过程出现小幅波动，并缓慢地向最优解逼近，而OC方法的收敛过程更加平稳，且更快地收敛。

图6　用OC和MMA求解最优值的迭代过程Fig.6 Iteration process by OC and MMA

双材料的拓扑构型见图7，图中白色代表基材料，黑色代表刚度材料。由拓扑构型可以看出，材料的分布与灵敏度分析结果一致，少部分刚度材料长条状分布在板的上方和右侧，大部分聚集在板中心和其左下方位置，并且与左边界和下边界处的刚度材料连为一体。从图3中可以看出，优化后除了板左下方区域外，其它区域声压级均减小，最小声压级位置由中心向右上方偏移，右上方区域的声压级降低较多，目标声压级明显降低。双材料的拓扑优化方法对原结构的刚度重新分布，改变声场内声压级的分布，进而降低目标位置的声压级。

图7　双材料的拓扑分布Fig.7 Distribution of bi-material

5.2声场平均声压级的拓扑优化

5.2.1集中力作用下的拓扑优化

顶板中心作用幅值0.1 N的简谐激励，声场的平均声压级作为优化的目标函数。算例展示了激励频率为20 Hz， 55 Hz， 90 Hz， 125 Hz， 160 Hz和195 Hz的双材料拓扑分布，如图8所示，可以看出拓扑构型与激励频率相关，频率越高拓扑构型越复杂，刚度材料以激励点为中心成对称分布，且在激励作用点处始终有刚度材料。表1给出了目标函数和约束函数优化前和优化后的结果。结合图9和表1可见，频率为20 Hz， 55 Hz和90 Hz的声压级减少量远小于频率为125 Hz， 160 Hz和195 Hz的声压级减少量。

(a) f=20 Hz　　　(b) f=55 Hz　　　(c) f=90 Hz

(d) f=125 Hz　　　(e) f=160 Hz　　　(f) f=195 Hz图8　双材料的拓扑分布Fig.8 Distribution of bi-material

频率/Hz初始设计目标函数/dB结构重量/kg最优设计目标函数/dB结构重量/kg迭代步数2091.060.9890.510.983355101.590.9899.110.98209091.220.9888.720.9821125103.770.9894.010.9825160104.600.9897.320.9828195103.320.9896.550.9826

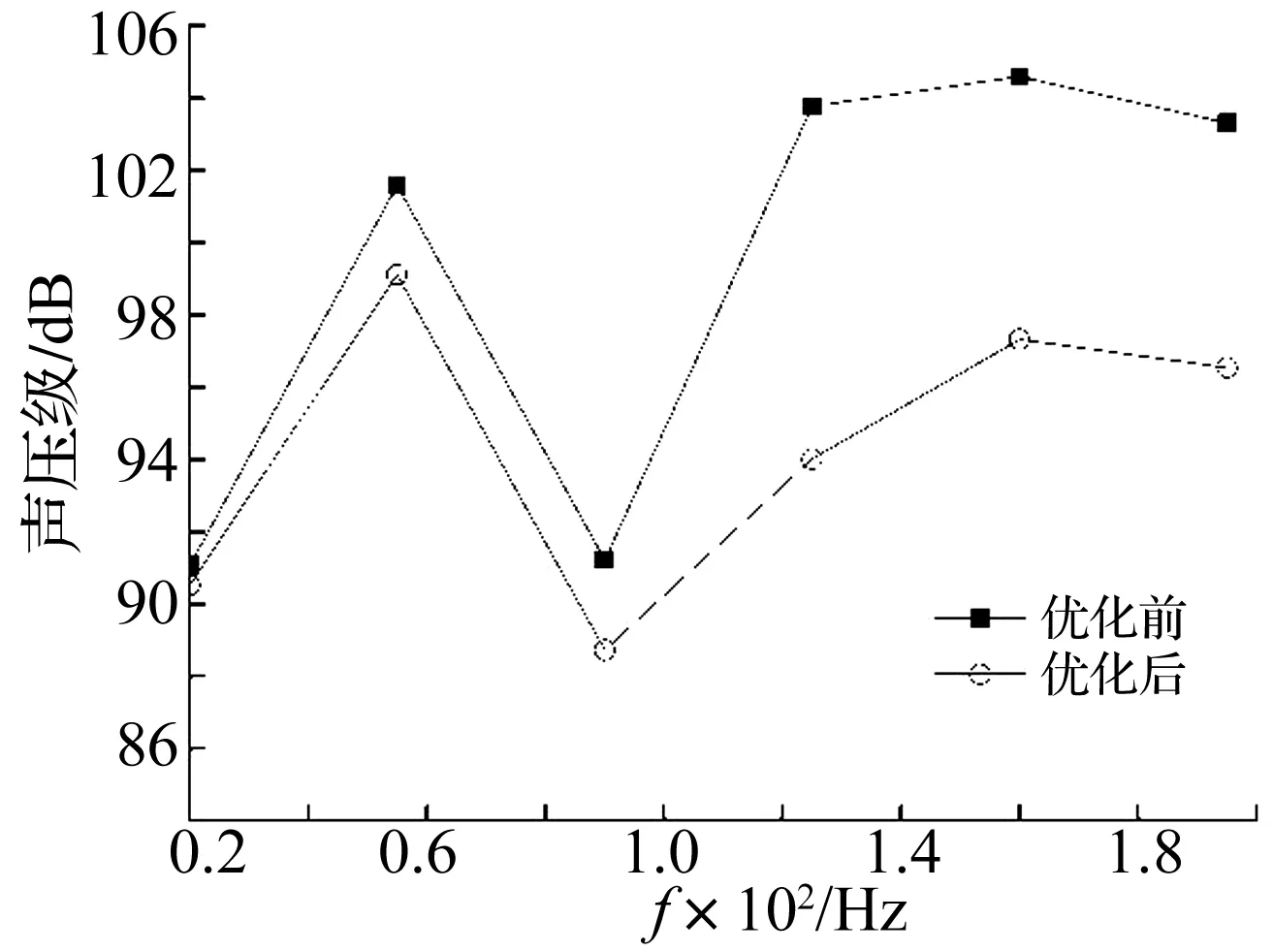
图9　优化前后声场的平均声压级Fig.9 Average sound pressure level before and after optimization

5.2.2均布面压力下拓扑优化

声场的平均声压级作为优化的目标函数。1 000 Pa的均布面荷载作用在顶面上，激励频率分别为20 Hz， 55 Hz， 90 Hz， 125 Hz， 160 Hz和195 Hz。如图10所示，拓扑构型随频率变化。表2给出了目标函数和约束函数优化前和优化后的结果。结合图11和表2可见，频率为20 Hz， 55 Hz和90 Hz的声压级减少量远小于频率为125 Hz， 160 Hz和195 Hz的声压级减少量。较高的外部激励频率能激起结构较高阶的特征模态，结构的振动形态越复杂，刚度的改变对结构振动响应的影响也越大，优化后声压级的降低也更明显。

(a) f=20 Hz　　　(b) f=55 Hz　　　(c) f=90 Hz

(d) f=125 Hz　　　(e) f=160 Hz　　　(f) f=195 Hz图10　双材料的拓扑分布Fig.10 Distribution of bi-material

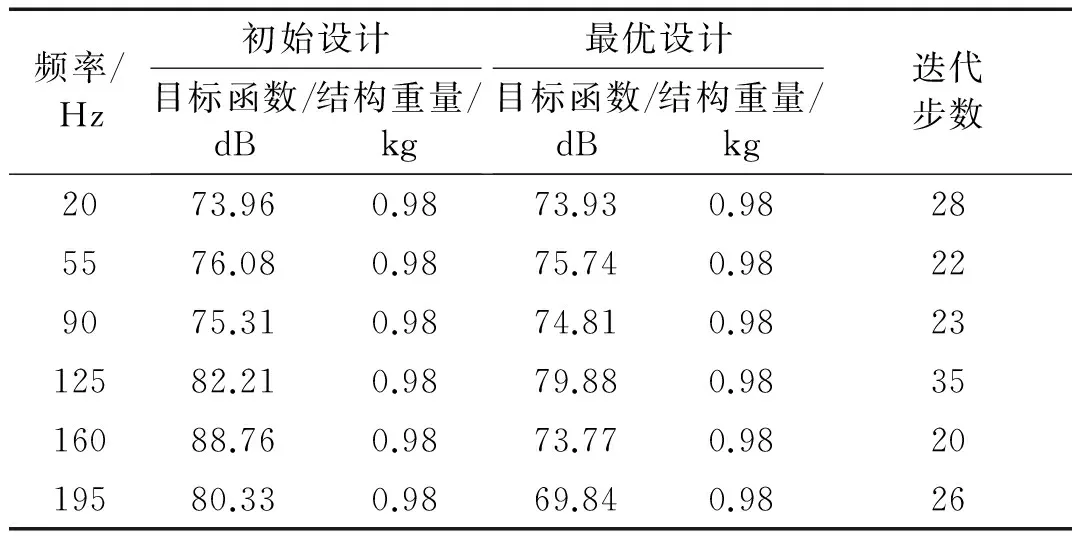
频率/Hz初始设计目标函数/dB结构重量/kg最优设计目标函数/dB结构重量/kg迭代步数2073.960.9873.930.98285576.080.9875.740.98229075.310.9874.810.982312582.210.9879.880.983516088.760.9873.770.982019580.330.9869.840.9826

图11　优化前后声场的平均声压级Fig.11 Average sound pressure level before and after optimization

5.3频率段激励下平均声压级的拓扑优化

在顶板中心作用的集中力幅值为0.1 N，频率在120～130 Hz和130～140 Hz两个频带上，分别选取120～130 Hz频带上的平均声压级和130～140 Hz频带上的平均声压级为优化目标，刚度材料重量为约束函数，优化的刚度材料拓扑分布如图12所示。图13展示了不同的优化目标对声压级曲线的影响，实曲线代表优化前声压级曲线；点曲线代表优化120～130 Hz的平均声压级的声压级曲线，可以看出它在120～130 Hz范围内比实曲线明显降低，但是在超出130 Hz的位置会高于实曲线，而且峰值位置向高频方向移动；虚曲线代表优化130～140 Hz的平均声压级的声压级曲线，同样可以看到它在130～140 Hz范围内明显低于实曲线，在小于这个频带范围的位置会高于实曲线，峰值位置向低频方向迁移。这说明了在满足优化目标降低的同时可能会导致其他位置响应的提高，因此在研究声结构耦合系统的优化时，必须要明确优化目标的频率范围，否则可能不仅没有降低目标的噪声，反而增大了噪声。

图12　双材料的拓扑分布Fig.12 Distribution of bi-material

图13　不同频带激励下初始和优化后的平均声压级Fig.13 Average sound pressure level of the initial and the optimized under different frequency band

6　结　论

本文主要研究了声结构耦合系统双材料模型的拓扑优化方法。基于微结构设计域法，构建了双材料优化模型。推导了关于声压级的伴随灵敏度分析方法，通过与有限差分法作比较，验证了伴随灵敏度计算的高精确和高效率并且推导了放松形式的最优准则法，并与移动渐近线法比对，得到了放松形式的最优准则法在求解声结构耦合问题时具有收敛快，算法稳定的特点。数值结果证明本文提出的优化方法既可降低封闭腔体内某点的声压级，也可以降低整个腔内的平均声压级。刚度材料的拓扑构型不仅取决于加载的是集中力或是面力，而且与作用频率相关，高频时降噪效果更明显。针对不同频率或频率段的声压级进行优化会得到不同的声压级曲线，因此明确优化的声压级频率是声结构耦合系统拓扑优化方法有效的关键。

[1] BENDSØE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method [J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[2] SIGMUND O. A 99 line topology optimization code written in Matlab [J]. Struct Multidiscip O, 2001,21(2):120-127.

[3] ANDREASSEN E, CLAUSEN A, SCHEVENELS M, et al. Efficient topology optimization in MATLAB using 88 lines of code [J]. Struct Multidiscip O, 2011, 43(1): 1-16.

[4] MIN S, KIKUCHI N, PARK Y, et al. Optimal topology design of structures under dynamic loads [J]. Structural Optimization, 1999, 17(2/3): 208-218.

[5] JOG C. Topology design of structures subjected to periodic loading [J]. Journal of Sound and Vibration,2002,253(3): 687-709.

[6] GUO Xu, CHENG Geng-dong, YAMAZAKI K. A new approach for the solution of singular optima in truss topology optimization with stress and local buckling constraints [J]. Structural and Multidisciplinary Optimization, 2001, 22(5): 364-373.

[7] LEE J, WANG S, DIKEC A. Topology optimization for the radiation and scattering of sound from thin-body using genetic algorithms [J]. Journal of Sound and Vibration, 2004, 276(3/4/5): 899-918.

[8] KANG Zhan, ZHANG Xiaopeng, JIANG Shigang, et al. On topology optimization of damping layer in shell structures under harmonic excitations [J]. Structural and Multidisciplinary Optimization, 2012, 46(1): 51-67.

[9] DU J, OLHOFF N. Topological design of vibrating structures with respect to optimum sound pressure characteristics in a surrounding acoustic medium [J]. Struct Multidiscip O, 2010, 42(1): 43-54.

[10] AKL W, EL-SABBAGH A, AL-MITANI K, et al. Topology optimization of a plate coupled with acoustic cavity [J]. International Journal of Solids and Structures,2009,46(10):2060-2074.

[11] SHU L, WANG M Y, MA Z D. Level set based topology optimization of vibrating structures for coupled acoustic-structural dynamics [J]. Computers & Structures, 2014, 132:34-42.

[12] LIU Baoshan, ZHAO Guozhong, SHI Lei. Design optimization of acoustic radiation from structures under random excitation [J]. Noise Control Eng, 2010, 58(2): 132-144.

[13] YANG R Z, DU J B. Microstructural topology optimization with respect to sound power radiation [J]. Struct Multidiscip O, 2013, 47(2): 191-206.

[14] NIU B, OLHOFF N, LUND E, et al. Discrete material optimization of vibrating laminated composite plates for minimum sound radiation [J]. International Journal of Solids and Structures, 2010, 47(16): 2097-2114.

[15] 刘海, 高行山, 王佩艳, 等.基于拓扑优化的结构加强筋布局降噪方法研究 [J]. 振动与冲击, 2013,32(13):62-65.

LIU Hai, GAO Xingshan, WANG Peiyan, et al. Stiffeners layout design for noise reduction using topology optimization [J]. Journal of Vibration and Shock,2013,32(13):62-65.

[16] LUO J, GEA H C. Optimal stiffener design for interior sound reduction using a topology optimization based approach [J]. Transactions-American Society of Mechanical Engineers Journal of Vibration and Acoustics, 2003, 125(3): 267-73.

[17] VENKAYYA V. Optimality criteria: a basis for multidisciplinary design optimization [J]. Computational Mechanics, 1989, 5(1): 1-21.

[18] CRAGGS A. The transient response of a coupled plate-acoustic system using plate and acoustic finite elements [J]. Journal of Sound and Vibration, 1971, 15(4): 509-528.

[19] GEA H C. Topology optimization: a new microstructure-based design domain method [J]. Computers & Structures, 1996, 61(5): 781-788.

[20] MA Z D, KIKUCHI N, CHENG H C. Topological design for vibrating structures [J]. Computer Methods in Applied Mechanics and Engineering, 1995, 121(1): 259-280.

Topology optimization of a bi-material model for acoustic-structural coupled systems

SHANG Linyuan1， ZHAO Guozhong1， CHEN Gang2

(1. State Key Laboratory of Structural Analysis for Industrial Equipments,Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China;2. Shanghai Turbine Plant, Shanghai Electric Power Generation Equipment Co., Ltd., Shanghai 200240, China)

A bi-material topology optimization approach was investigated based on the microstructure-based design domain method with the combination of an adjoint method and a relaxed form of optimality criteria. An adjoint sensitivity method whereby sound pressure level derivative with respect to topology variables was proposed and deduced. A relaxed form of optimality criteria was deduced and used to solve the optimization problem of the coupled systems. Numerical examples show the high efficiency and the high accuracy of the adjoint sensitivity analysis, and the quick convergence and the high stability of the relaxed form of optimality criteria. The results also show that the topology optimization method of bi-material reduces internal noise and validates the optimization method.

acoustic-structural coupled systems; topology optimization; adjoint method; optimality criteria; bi-material model

国家自然科学基金(11072049);国家重点基础研究发展计划(2010CB832703)

2014-12-19修改稿收到日期：2015-03-10

商林源 男，博士生，1987年生

赵国忠 男，博士，教授，博士生导师，1972年生E-mail: zhaogz@dlut.edu.cn

TB533

A

10.13465/j.cnki.jvs.2016.16.031