基于数学形态梯度谱熵的性能退化特征提取方法及其应用

刘　鹏， 李洪儒， 许葆华

(军械工程学院，石家庄　050003)



基于数学形态梯度谱熵的性能退化特征提取方法及其应用

刘鹏， 李洪儒， 许葆华

(军械工程学院，石家庄050003)

针对数学形态谱熵难以准确描述信号的形态复杂度以及性能退化趋势评价效果不理想的问题，提出一种基于数学形态梯度谱熵的性能退化特征提取方法。该方法利用形态梯度算子在信号处理中能有效提取故障特征信息并抑制噪声的优势，将其引入到形态谱熵的定义中，得到数学形态梯度谱熵的概念。通过对仿真信号进行分析，验证了所提出的形态梯度谱熵作为信号复杂度指标的合理性与有效性。最后，将该方法应用到滚动轴承的性能退化研究中，结果表明，形态梯度谱熵能有效反映滚动轴承的性能退化趋势。

性能退化；特征提取；形态谱熵；形态梯度谱熵；滚动轴承

如何有效提取反映机械设备运行状态与规律的特征，一直是故障诊断领域的研究热点与难点。传统特征提取技术侧重于对不同故障类型的区分，而性能退化特征的着眼点在于该特征信息能否反映设备性能退化程度的量化反映能力。徐东等[1]通过改进的经验模态分解方法分解轴承振动信号，计算各本征模态的均方根值、峭度等时域指标作为表征滚动轴承运行状态的性能退化指标；张龙等[2]通过粗粒化过程，在多尺度熵的基础上，提出了一个新的故障程度定量表征指标—多尺度熵偏均值，该指标能够发现轴承的早期故障，并且很好地跟踪故障的发展趋势。

数学形态学是一种非线性信号处理的工具，能够把一个复杂信号分解为具有物理意义的部分，并将其与背景剥离，同时保持其主要的形状特性，在信号处理和故障诊断中得到了普遍应用[3-10]。以数学形态学为基础，结合分形和信息熵等理论，王书涛等[5]以形态分形维数和形态谱熵为特征向量，在滚动轴承故障诊断中取得了不错的效果；王冰等[6]提出一种基于多尺度形态分解谱熵的特征提取方法，可以有效表征滚动轴承的性能退化程度。

基于上述研究成果，在形态谱以及形态谱熵的理论研究基础上，以形态梯度算子为核心，提出一种基于形态梯度谱熵的性能退化特征提取方法，并通过仿真与实例信号进行有效性验证。

1　理论基础

1.1多尺度数学形态学

多尺度运算采用不同尺度的结构元素对信号进行变换，能够实现对信号不同尺度结构特征下的处理和分析。假设离散信号为f(n)，n=0,1,…,N-1，λ为分析尺度，g为单位结构元素，即分析尺度为1时的结构元素，则在λ尺度下的结构元素定义为：

λg=g⊕g…⊕g

(1)

式中:共进行λ-1次膨胀运算。

以此为基础，对离散信号序列为f(n)的多尺度形态腐蚀、膨胀、开和闭运算可分别定义如下：

(2)

1.2形态谱和形态谱熵

令f(n)为时域中的一非负函数，g(m)为一凸结构函数。则f(n)的形态谱可由下式计算而得。

(3)

式中:A(f)表示f在定义域内的面积。当λ≥0时，为开运算形态谱，记为PS+(f,λ,g)，当λ<0时，为闭运算形态谱，记为PS-(f,λ,g)。

与频谱能直观反映信号中存在的频率成分一样,建立在多尺度形态学理论上的形态谱，亦能反映信号不同尺度结构元素的形态运算下形状的变化信息[5]。对于一维离散信号，由于尺度大小只取连续的整数值，因此形态谱的定义可简化为：

PS+(λ,g)=A[f○λg-f○ (λ+1)g],

0≤λ≤λmax

(4)

PS-(λ,g)=A[f•(-λ)g-f•(-λ+1)g],

λmin≤λ≤0

(5)

形态谱熵描述了形态谱值的稀疏程度，即信号不同形态形状概率分布的有序程度，形态谱熵的定义为：

(6)

式中:q(λ)=PS(λ,g)/∑PS(λ,g)，将PSE除以ln(λmax-λmin+1)便可以得到归一化的形态谱熵。

综上所述，形态开、闭运算是形态谱和形态谱熵分析的核心。通过多尺度形态开运算，可以得到一组随结构元素尺度增大而递减的灰度值。由于形态开运算只能平滑信号中的正向脉冲以及闭运算只能平滑信号中的负向脉冲，因此，形态开、闭在信号分析处理中存在统计偏倚现象[7]，若采集的振动信号中含大量噪声成分，具有特定形态特征的故障信号很可能会淹没在强烈背景噪声中，而直接影响到信号处理的准确性。

2　基于数学形态梯度谱熵的性能退化特征提取方法

2.1形态梯度算子

形态梯度算子定义为信号f通过结构元素g膨胀和腐蚀运算后的差分，其定义如下：

Grad(f)=f⊕g-fΘg

(7)

形态梯度常作为图像处理中的边沿检测工具。如果在某一点处的梯度值大，则表明该点处图像的明暗变化迅速，从而可能会有边沿通过。在信号处理中，形态梯度算子是凸显脉冲信息的有力工具，可用来检测并提取出稳态信号上的暂态信息，因此能有效地检测出脉冲的位置与形状[7-9]。

实际采集的旋转机械故障振动信号一般包含大量噪声成分，必会影响形态谱和形态谱熵分析结果的准确性。基于形态梯度的上述特性，本节将形态梯度算子推广应用到形态谱分析中，得到形态梯度谱的概念，以此为基础，提出基于形态梯度谱熵的性能退化特征提取方法，并验证其有效性。

2.2形态梯度谱与形态梯度谱熵

令f为时域中的一非负函数，g为一凸的结构函数。根据上述形态谱的定义，形态梯度谱的定义可以描述如下：

PGS(f,λ,g)=

(8)

由形态谱的定义可知，数学形态谱是由正、负两个区间构成的，形态谱的正区间表示信号本身的结构特征信息，而负区间表示的是相应的背景信息，由于形态开、闭运算具有对偶性，所以两者表示的对象是一致的，一般只研究形态谱的正区间。同理，对于形态梯度谱，只对其正区间进行研究。

对于一维离散信号，与形态开算子的非外延性相反，形态梯度算子具有外延性，因此，离散的形态梯度谱则简化为：

PGS+(λ,g)=S[(f⊕(λ+1)g-fΘ(λ+1)g)-

(f⊕λg-fΘλg)]

(9)

PGS-(λ,g)=S[(fΘ(-λ+1)g-f⊕(-λ+1)g)-

(fΘ(-λ)g-f⊕(-λ)g)]

(10)

形态梯度谱熵的定义则为：

(11)

式中:q(λ)=PGS(λ,g)/∑PGS(λ,g)，将PGSE除以ln(λmax-λmin+1)便得到归一化的形态梯度谱熵。形态梯度谱熵反映了信号的形态特征及组成变化情况，也是从本质上描述信号的一种复杂度指标。

3　仿真分析

为验证形态梯度谱熵对性能退化趋势的反映能力，采用仿真信号[1]对其进行有效性研究，仿真信号表达式如下：

x(t)=2cos(2π*50t)+

0.1t2cos(2π*10t+2)+y(t)

(12)

式中：2cos(2π*50t)为常规的振动信号，0.1t2cos(2π*10t+2)为故障模拟信号，用幅值0.1t2来近似反映故障随时间的变化过程，y(t)代表高斯噪声。信号采样点数为N=12 288，采样频率为f=1 024 Hz。图1显示了噪声强度为1时的仿真信号时域波形。将信号等分为12段并依次按顺序标记，每段采样点数为1 024，用这12组数据近似描述仿真信号故障程度不断加深的性能退化过程，组别越高，其性能退化程度也越深。

图1　仿真信号时域图Fig.1 Time domain wave of simulation signal

对仿真信号进行分析，根据以往文献资料[10-12]，选取计算简单的选取扁平型结构元素g=[0,0,0]，尺度从1连续变化到24。分别计算每组不同性能退化程度仿真数据的数学形态谱，见图2。从图中可以看出，随着结构元素尺度的变化，数学形态谱曲线受噪声影响，波动较大，且不同组别的数学形态谱曲线交织在一起，区分性差，难以准确定性定量区分不同的性能退化程度。

图2　12组仿真数据的形态谱曲线Fig.2 Morphological spectrum curves of 12 groups’ simulation data

保持结构元素以及结构尺度的取值不变，分别计算12组不同性能退化程度的仿真数据的形态梯度谱，结果见图3。与图2所示的数学形态谱曲线相比，形态梯度谱曲线随着结构元素的增大而呈现有规律地下降。对不同性能退化程度的仿真数据而言，形态梯度谱曲线区分更为明显，且随着故障程度加深，其内部包含特定尺度元素的成分就越多，下降趋势趋于平稳，幅值整体上呈现上升的趋势。

在形态谱和形态梯度谱熵的基础上，分别计算各组数据的形态谱熵以及形态梯度谱熵，结果见图4。随着性能退化程度的加深，12组仿真数据的形态谱熵变化不大，受噪声影响存在波动，很难定性区分不同的性能退化程度；而形态梯度谱熵值呈不断增大的趋势，与性能退化趋势具有良好的关联性。

可以得知，与形态梯度谱熵相比，形态谱和形态谱熵未能充分挖掘信号中的特征信息，较难准确描述信号的形态复杂度，因此，性能退化趋势的评价效果不佳。

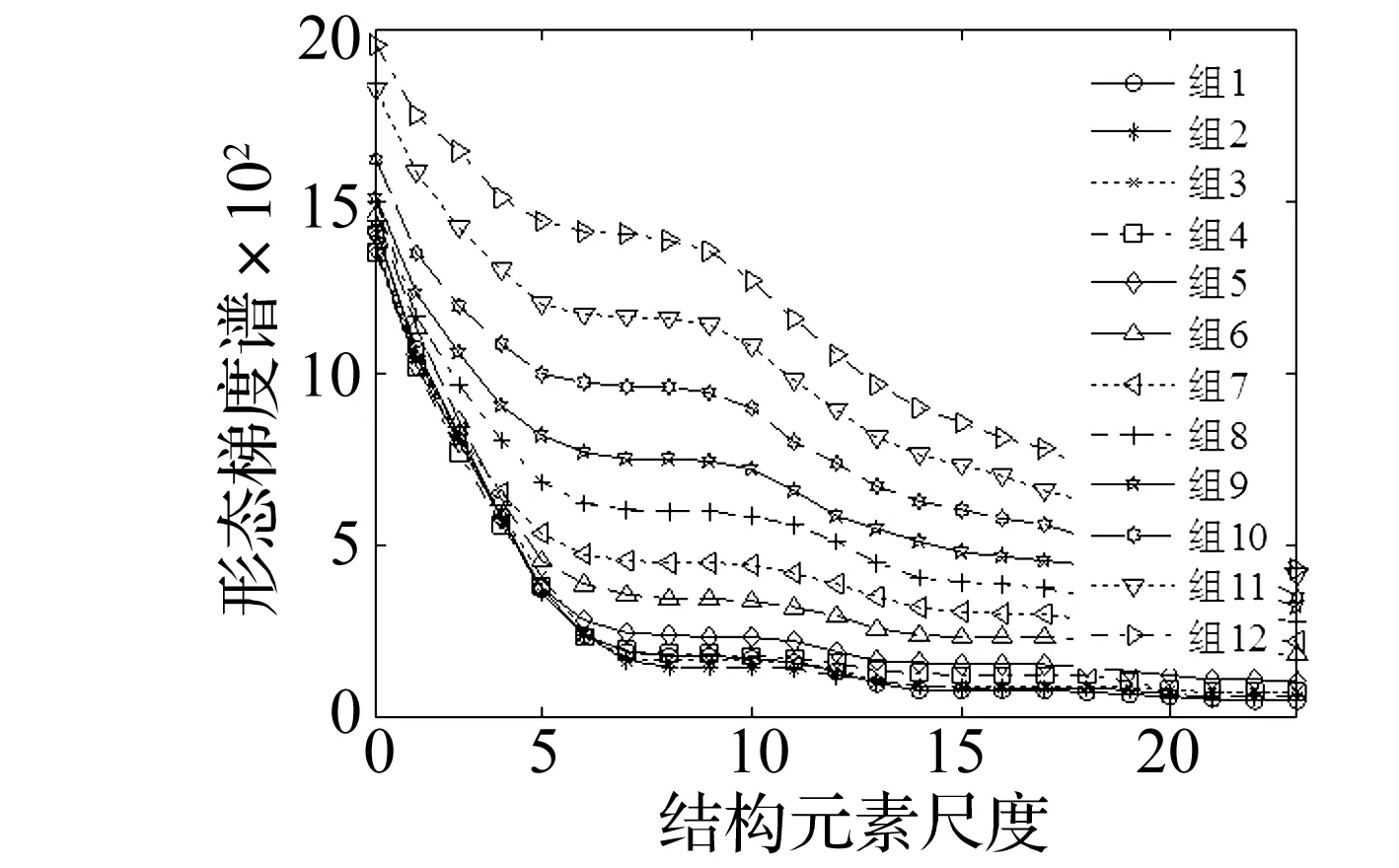
图3　12组仿真数据的形态梯度谱曲线Fig.3 Morphology gradient spectrum curves of 12 groups’ simulation data

图4　12组仿真数据的形态谱熵与形态梯度谱熵的分析结果Fig.4 Morphological spectrum entropy and morphological gradient spectrum entropy result of 12 groups’ simulation data

4　实例分析

为进一步验证数学形态梯度谱熵表征滚动轴承性能退化趋势的有效性，本文应用美国凯斯西储大学电气工程实验室的滚动轴承实验数据[13]和美国国家宇航局(NASA)预诊断数据库的轴承全寿命数据[14]进行分析。

首先对美国凯斯西储大学的轴承实验数据进行分析，实验的对象为深沟球轴承。轴承局部损伤是由电火花机在轴承内圈上人工加工而成的，直径0.18 mm，0.54 mm分别用于模拟滚动轴承内圈轻度和重度两种不同损伤程度。按时间顺序以6 000个采样值为1组，分别选取轴承内圈不同受损状态下(包括正常状态)的振动信号各20组进行损伤程度分析。同样选取计算简单的扁平型结构元素g=[0,0,0]，最大尺度设定为24。

从轴承3种不同受损状态下随机选取一种信号，其时域波形图见图5。计算其形态梯度谱，结果见图6，可以看出，损伤程度越大，形态梯度谱幅值越大，不同损伤状态信号的形态梯度谱曲线区分显著。

图5　不同损伤程度状态下内圈信号时域波形图Fig.5 Time domain waves of inner race fault with different severity

分别对轴承3种不同受损状态共60组的振动信号进行形态梯度谱熵分析，见图7。从图中可以看出，随着损伤程度的加深，数学形态梯度谱熵的取值不断增大，与仿真信号结果一致。

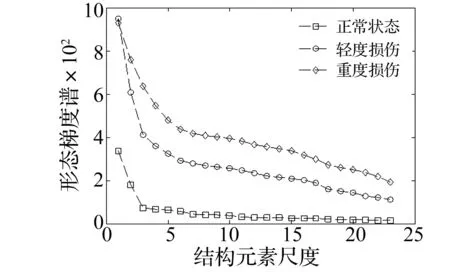
图6　不同损伤程度状态下内圈信号的形态梯度谱曲线Fig.6 Morphological spectrum curve of inner race fault with different severity

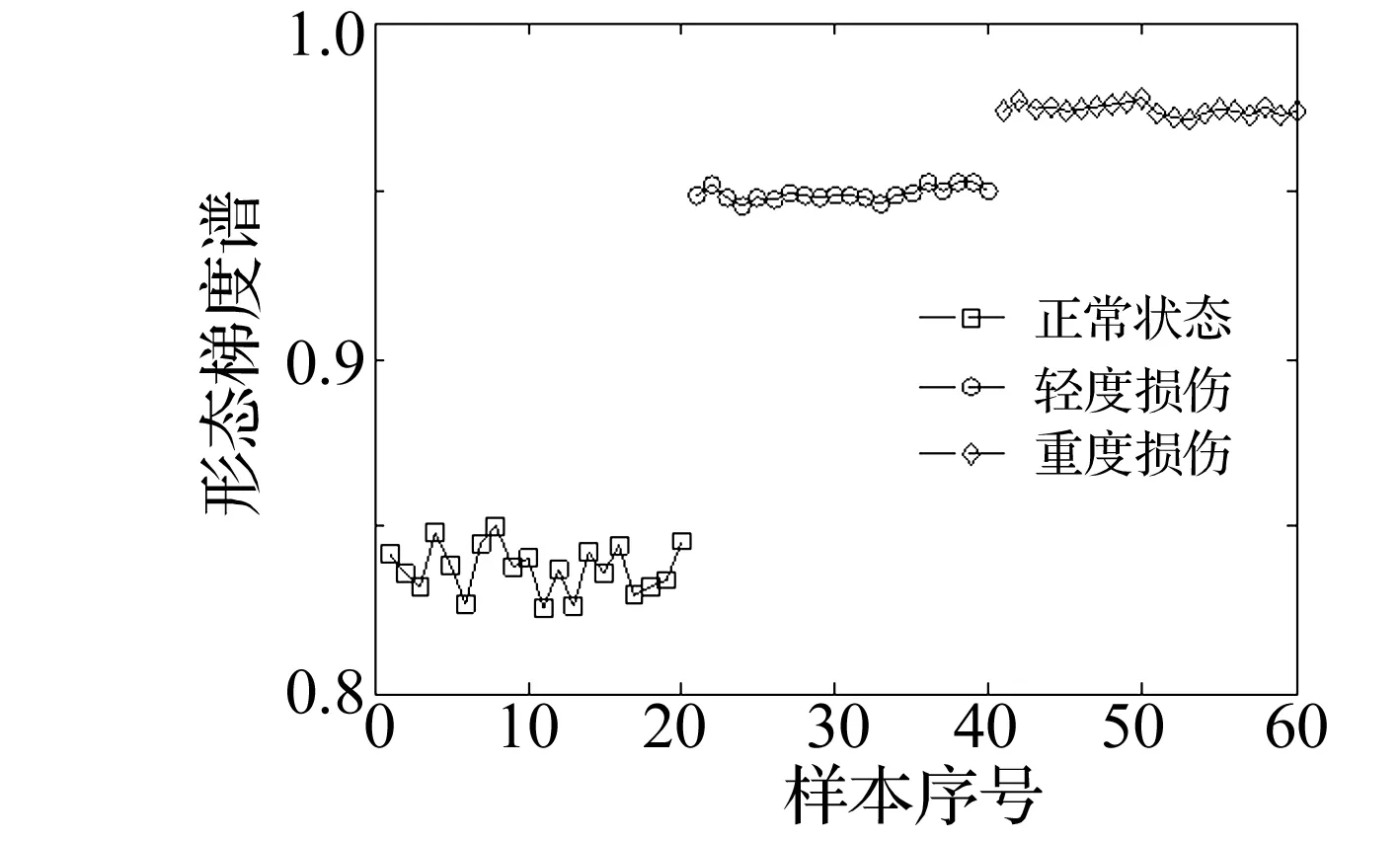
图7　不同损伤程度状态下内圈信号的形态梯度谱熵Fig.7 Morphological gradient spectrum entropy of inner race fault with different severity

其次，按照形态梯度谱熵的计算方法对美国国家宇航局(NASA)预诊断数据库的轴承全寿命数据进行分析，实验过程中采样频率为20 000 Hz，期间每隔10 min采集振动信号一次，总共采集到984个数据文件。停机解体后发现轴承的失效形式为严重的外圈剥落故障。

计算轴承全寿命实验数据的形态梯度谱熵，并进行5点平滑处理，结果见图8。从图中可以看出，在第700个样本左右形态梯度谱熵开始出现波动，在第800个样本后开始有持续上升的趋势，在第900个样本后急剧上升，并出现较大的波动。可以表明，随着轴承性能退化程度的加剧，形态梯度谱熵能较早地发现早期故障，并且正确跟踪轴承性能退化的发展趋势。

形态谱熵在全寿命数据中的变化情况见图9，大约在900个样本后才开始有明显上升的趋势。与形态梯度谱熵相比，形态谱熵识别早期故障的能力不强，在性能退化趋势的评价效果上不是很理想。

图8　形态梯度谱熵在轴承全寿命数据中的变化Fig.8 Variation of morphological gradient spectrum entropy in bearing life-cycle data

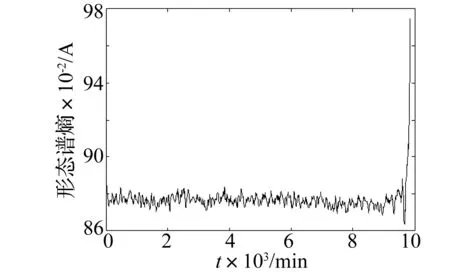
图9　形态谱熵在轴承全寿命数据中的变化Fig.9 Variation of morphological spectrum entropy in bearing life-cycle data

综合分析上述仿真与实例结果，可以得知，与形态谱熵相比，形态梯度谱熵在反映滚动轴承的性能退化趋势上具有更好的效果。

5　结　论

(1)本文在形态谱以及形态谱熵的基础上，以形态梯度算子为核心，提出了一个新的性能退化程度定量表征指标——数学形态梯度谱熵。

(2)通过对仿真信号进行分析，验证了形态梯度谱熵作为信号复杂度指标的合理性与有效性。与形态谱熵相比，形态梯度谱熵能有效提取信号在多个尺度上的非线性复杂度信息，更好地表征信号的性能退化趋势。

(3)将数学形态梯度谱熵应用到滚动轴承的性能退化研究中，结果表明，该指标能较早地发现早期故障，与滚动轴承性能退化趋势能保持较好的一致性。

[1] 徐东, 徐永成, 陈循, 等. 基于EMD的灰色模型的疲劳剩余寿命预测方法研究 [J]. 振动工程学报, 2011, 24(1): 104-110.

XU Dong,XU Yongcheng, CHEN Xun, et al. Residual fatigue life prediction based on grey model and EMD [J]. Journal of Vibration Engineering, 2011, 24(1): 104-110.

[2] 张龙, 黄文艺, 熊国良. 基于多尺度熵的滚动轴承故障程度评估 [J]. 振动与冲击, 2014, 33(9): 185-189.

ZHANG Long, HUANG Wenyi, XIONG Guoliang, et al. Assessment of rolling element bearing fault severity using multi-scale entropy [J]. Journal of Vibration and Shock, 2014, 33(9): 185-189.

[3] LI Q Y, XU J, WANG W H, et al. Slope displacement prediction based on morphological filtering [J]. Journal of Central South University, 2013, 20: 1724-1730.

[4] RAJ S, MURALI N. Early classification of bearing faults using morphological operators and fuzzy inference [J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 567-574.

[5] 王书涛, 张金敏, 李圆圆, 等. 基于数学形态学和模糊聚类的旋转机械故障诊断 [J]. 仪器仪表学报,2012,33(5): 1054-1061.

WANG Shutao, ZHANG Jinmin, LI Yuanyuan, et al. Rotating machinery fault diagnosis based on mathematical morphology and fuzzy clustering [J]. Chinese Journal of Scientific Instrument, 2012, 33(5): 1054-1061.

[6] 王冰, 李洪儒, 许葆华. 基于多尺度形态分解谱熵的电机轴承预测特征提取及退化状态评估 [J]. 振动与冲击, 2013, 32(22): 124-128.

WANG Bing, LI Hongru, XU Baohua. Motor bearing forecast feature extracting and degradation status identification based on multi-scale morphological decomposition spectrum entropy [J]. Journal of Vibration and Shock, 2013, 32(22): 124-128.

[7] LI B, ZHANG P L, WANG Z J. A weighted multi-scale morphological gradient filter for rolling element bearing fault detection [J]. ISA Transactions, 2011, 50: 599-608.

[8] 刘东升, 李元, 杨博文, 等. 基于自适应多尺度形态梯度与非负矩阵分解的轴承故障诊断 [J]. 振动与冲击,2013,32(19):106-110.

LIU Dongsheng, LI Yuan, YANG Bowen, et al. Bearing fault diagnosis based on adaptive multi-scale morphological gradient and non-negative matrix factorization [J]. Journal of Vibration and Shock, 2013, 32(19): 106-110.

[9] 李兵, 高敏, 张旭光, 等. 用形态梯度法与非负矩阵分解的齿轮故障诊断 [J]. 振动、测试与诊断, 2014, 34(2): 295-300.

LI Bing, GAO Min, ZHANG Xuguang, et al. Gear fault diagnosis based on adaptive multi-scale morphological gradient and non-negative matrix factorization [J]. Journal of Vibration, Measurement and Diagnosis, 2014, 34(2):295-300.

[10] DONG Y B, LIAO M F. Fault diagnosis of rolling element bearing based on modified morphological method [J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1276-1286.

[11] ZHANG Y D, WU L A. Recursive structure element decomposition using migration fitness scaling genetic algorithm [J]. Advances in Swarm Intelligence, 2011,6728:514-512.

[12] 姜万录, 郑直, 朱勇, 等. 基于最优扁平型结构元素长度的液压泵故障诊断研究 [J]. 振动与冲击, 2014, 33(15): 35-41.

JIANG Wanlu, ZHENG Zhi, ZHU Yong, et al. Hydraulic pump fault diagnosis based on optimal flat structure element length[J]. Journal of Vibration and Shock, 2014, 33(15): 35-41.

[13] LEE J, QIU H, YU G, et al. Rexnord technical services: ‘bearing data set’, IMS, University of Cincinnati [EB/OL].NASA Ames Prognostics Data Repository. http://ti.arc.nasa.gov/project/prognostic-data-repository.

[14] LOPARO K A. Bearing data center [EB/OL]. Case Western Reserve University. http://www.eecs.cwru. edu/laboratory/bearing.

A performance degradation feature extraction method and its application based on mathematical morphological gradient spectrum entropy

LIU Peng, LI Hongru, XU Baohua

(Ordnance Engineering College, Shijiazhuang 050003, China)

Aiming at that morphology spectrum entropy fails to accurately describe the morphological complexity of signals and its evaluation effect of performance degradation trend is not ideal, a performance degradation feature extraction method based on mathematical morphological gradient spectrum entropy was proposed in this work. Morphological gradient algorithm which could effectively extract fault feature information and remove interference components in the signal processing was introduced into the definition of morphology spectrum entropy. The concept of mathematical morphological gradient spectrum entropy was thus obtained. The simulations verify the rationality and effectiveness of the morphological gradient spectrum entropy as a signal complexity index. Lastly the rolling bearing performance degradation study results prove that the morphological gradient spectrum entropy can describe rolling bearing’s performance degradation trend.

performance degradation; feature extraction; morphological spectrum entropy; morphological gradient spectrum entropy; rolling bearing

国家自然科学基金资助项目(51275524)

2015-07-06修改稿收到日期：2015-09-06

刘鹏 男，硕士，1991年3月生

李洪儒 男，博士，教授，博士生导师，1963年1月生

TH165；TN911

A

10.13465/j.cnki.jvs.2016.16.015