压电材料中多个孔边径向裂纹的动力相互作用

李　冬， 王慧聪， 宋天舒

(1. 河北交通职业技术学院 土木工程系，石家庄　050091；2. 哈尔滨工程大学 航天与建筑工程学院，哈尔滨　150001)



压电材料中多个孔边径向裂纹的动力相互作用

李冬1， 王慧聪1， 宋天舒2

(1. 河北交通职业技术学院 土木工程系，石家庄050091；2. 哈尔滨工程大学 航天与建筑工程学院，哈尔滨150001)

采用Green函数法对压电材料中多个孔边径向裂纹在SH波作用下的相互作用问题进行了研究。首先利用复变函数方法构造出具有多个半圆形凹陷的半无限压电介质的位移Green函数和电场Green函数，然后采用裂纹“切割”技术构造孔边径向裂纹，根据界面上的位移和应力连续性条件建立求解问题的第一类Fredholm定解积分方程。最后作为算例，给出了裂纹尖端动应力强度因子随缺陷几何尺寸、材料物理参数和入射波频率的变化特征图并进行了讨论。

压电材料；孔边径向裂纹；Green函数；动应力强度因子；SH波散射

压电材料具有独特的力电耦合性质，因此被广泛用于制作高精度位移器和传感器等电子元器件。但由于其本身呈脆性，压电材料制作的电子器件在工作过程中经常发生电致疲劳和电致断裂，因而对于压电材料及结构的力电耦合的静动力特性研究得到了普遍重视[1-3]。近年来，NARITA等[4]研究了电弹波作用下压电材料中单一裂纹的能量释放率问题；MEGUID等[5-6]对压电材料中多个裂纹在电弹波场作用下的动力反平面问题进行了研究；WANG[7]进一步对双相压电材料中多个界面裂纹相互作用的动力学问题进行了探讨；周振功等[8-9]分析了压电材料中两平行裂纹的相互影响问题。

以上研究均是把缺陷简化成直线型裂纹来进行研究，但是目前已有部分研究成果表明，将材料中的缺陷一律简化成直线型裂纹并不总是偏于安全的，比如孔边裂纹缺陷情况。GARCA-SNCHEZ等[10]对各向异性压电板中孔边裂纹的应力强度因子问题采用混合边界元的方法进行了数值分析；WANG等[11]利用保角映射和复变函数方法分析了无限大压电材料中圆孔边径向Ш型裂纹问题；GUO等[12-13]利用文献[11]中的方法对压电材料中椭圆孔边非对称双裂纹的反平面问题进行了探讨；宋天舒等[14-15]通过Green函数方法研究了压电材料中圆孔边径向Ш型裂纹在SH波作用下的动力反平面特性。

本文对含有多个圆孔边径向裂纹缺陷的横观各向同性压电材料的动力反平面问题进行了分析，讨论了在一组稳态电弹波场作用下，裂纹尖端的动应力强度因子随材料的几何参数、物理参数以及入射波频率等因素的变化规律。

1　力学模型与基本方程

含多个圆孔边径向有限长度裂纹的横观各向同性压电材料力学模型如图1所示。介质中含有N个圆孔边径向裂纹，且各裂纹均在一条直线上。沿裂纹方向建立xoy整体直角坐标系，并以各圆孔中心为原点建立局部坐标系xnonyn，各圆孔半径分别为Rn，孔边裂纹长度取为An，其中，n=1、2、…、N。相邻裂纹间的距离为d1、d2、…、dN-1，SH波与x轴呈角度a0入射，假定z轴为电极化方向。

图1　压电材料中多孔边径向裂纹模型Fig.1 Piezoelectric material with radial cracks emanating from the edges of circular cavities

在压电材料中，稳态的反平面动力学问题的控制方程为[6]：

c442w+e152φ+ρω2w=0,

e152w-κ112φ=0

(1)

式中：e15，κ11和c44分别为材料的压电系数、介电常数和弹性常数；w和φ为介质的出平面位移和平面内电势；ω和ρ为入射波圆频率和材料的质量密度。另外，这里省略了时间谐和因子exp(-iωt)，下同。

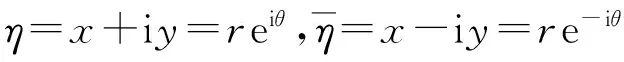
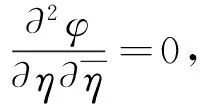
(2)

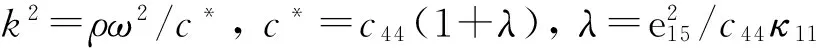
(3)

式中:τrz、τθz、Dr和Dθ分别为两个剪应力分量和两个电位移分量。

2　Green函数

本文Green函数采用的是具有多个半圆形凹陷的半无限压电介质在其水平表面任意一点η0处承受与时间谐和的出平面线源荷载δ(η-η0)作用时位移函数Gw和电势函数Gφ的基本解，满足控制方程式(2)的表达式由入射和散射两部分组成，分别用上标i和s表示[16]：

(4)

式中：

(5)

(6)

将式(4)代入本构方程式(3)，得到相应的应力和电位移表达式，利用边界条件(6)可得到求解未知系数的无穷代数方程组：

(7)

式中：

其中，κ0为圆孔内的介电常数。

利用周期函数的正交性，式(7)两边同乘e-inθ(n=0, ±1, ±2,…)，并在(-π,π)上积分可得：

(8)

式中：

3　定解积分方程

3.1圆孔对SH波的散射

一束稳态的SH波入射到含多个圆孔的无限域压电介质中，入射角度为a0，其产生的位移场和电势由入射和散射两部分组成。其中，入射位移场w(i)和电势φ(i)可写成[7]：

(9)

由圆孔产生的散射位移场w(s)和电势φ(s)可分别写为：

(10)

则含多个圆孔无限域压电介质中的总场为：

w(t)=w(i)+w(s)，φ(t)=φ(i)+φ(s)

(11)

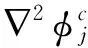
(12)

3.2定解积分方程的建立

根据已经得到的含多个圆孔的无限域压电介质中SH波入射时的总位移场和总电势以及半无限域中的Green函数，利用“裂纹切割”技术并结合“契合”思想[17]可构造得到压电介质中多个孔边径向导通裂纹对SH波散射的模型，其过程如图2所示。

图2　压电介质中裂纹切割与剖面契合模型Fig.2 The model of cracks’ division and section conjunction in a piezoelectric medium

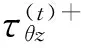
(13)

f+(r0,θ0)=f-(r0,θ0)=f(r0,θ0)

位移连续性条件为：

w(t+)+w(f+)+w(c+)=w(t-)+w(f-)+w(c-)

(14)

其中,

w(t+)=w(t-)=w(t)

w(f+)=∫Γ0f+(r0,π)Gw(r,θ;r0,π)dr0+

∫ΓNf+(r0,0)Gw(r,θ;r0,0)dr0

w(f-)=-∫Γ0f-(r0,π)Gw(r,θ;r0,π)dr0-

∫ΓNf-(r0,0)Gw(r,θ;r0,0)dr0

这里，

Γ0∈[R1+A1,∞];

Γn∈[Cn+Rn+An,Cn+Rn+An+dn];

ΓN∈[CN+RN+AN,∞];

Π1=Π2∈[R1,R1+A1];

Π2n-1∈[Cn-Rn-An,Cn-Rn];

Π2n∈[Cn+Rn,Cn+Rn+An];

其中，Cn为各圆孔中心到整体坐标系原点的距离，n=1,2,…,N。

由式(13)和(14)并结合上面几式便可得到求解未知力系f(r0,θ0)的定解积分方程：

∫Γ0f+(r0,π)Gw(r,θ;r0,π)dr0+

∫ΓNf+(r0,0)Gw(r,θ;r0,0)dr0=

θ=0,π

(15)

3.3动应力强度因子的定义与求解

附加的外力系f在裂纹尖端处具有平方根奇异性。引入孔边径向裂纹的动应力强度因子kⅢ如下：

(16)

式中:Sn=Cn-Rn-An或Cn+Rn+An(分别对应孔边裂纹的左端点和右端点)。

为了在定解积分方程中直接包含动应力强度因子以便于求解，对式(15)中的被积函数作如下代换：

(17)

代换后的定解积分方程在裂纹尖端处的数值结果即为动应力强度因子kⅢ的值。本文采用直接数值积分方法，利用散射波的衰减特性，把无穷积分方程转化为仅含有限项的线性代数方程，用Gauss消元法求解。

(18)

式中:τ0为入射波w(i)的应力幅值τ0=c*kw0。Q是特征参数，具有长度平方根的量纲。其值取SIH[18]在研究此类问题时给出的表达式：

(19)

4　算例和分析

作为算例，本文主要给出了双圆孔情况下，波垂直入射时，孔边径向裂纹内端点(图中B点所示)的动应力强度因子随圆孔半径、裂纹长度、入射波频率和压电常数等参数变化的数值结果。其中，各圆孔半径和孔边裂纹长度假定相等，分别用R和A表示。

图3给出了孔边径向裂纹和等效长度的直线型裂纹尖端的DSIF值在不同无量纲波数时，随A/R的变化。可以看到，两种模型下裂纹尖端的DSIF值大小交替变化，范围从-73%～98%。由此表明，“将非裂纹缺陷一律简化为Griffith裂纹是偏于安全的”假设并不总成立。

图4给出了A/R取不同值时，DSIF值随无量纲波数kR的变化情况。分析发现，当A/R=1 000，即退化到两直线型裂纹模型时，其值与文献[6]中的数据基本吻合。各DSIF值曲线随波数的增大而振荡衰减，其峰值随A/R减小而减小。当A/R=1.0和2.0时，其DSIF曲线峰值分别比A/R=1 000时的峰值大14%和31%。由此说明，当裂纹尺寸相对于圆孔半径相差不大时，圆孔对DSIF峰值的影响较明显。

图5给出了压电常数λ取不同值时，DSIF值的变化情况。由图可见，当波数kR=0.3左右时，各DSIF曲线取得峰值，且其值随λ增加而增大。当波数kR>0.6左右时，各曲线变化趋势刚好相反。随着波数的增加，以上变化趋势又重复出现。

图6给出了两圆孔边裂纹间相对距离d/R不同时，DSIF值的变化情况。可以看到，d/R值越小，DSIF峰值越大，表明两圆孔边裂纹间的相互作用越明显。随着无量纲波数的增加，各DSIF值曲线振荡衰减。

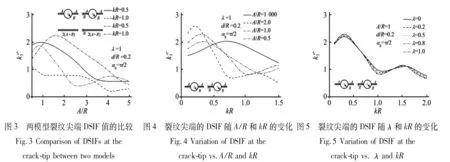
图6　裂纹尖端的DSIF随d/R和kR的变化Fig.6 Variation of DSIF at the crack-tip vs.d/R and kR

图7　不同裂纹数量下裂纹尖端的DSIF随kR的变化Fig.7 Variation of DSIF at the crack-tip vs. kR under different crack numbers

图7给出了不同孔边裂纹数量，各裂纹间距离均为d时，DSIF值随波数kR的变化情况。由图可见，孔边裂纹数目为1时，其DSIF值曲线与文献[14]中的结果基本吻合，进一步验证了计算结果的正确性。各曲线峰值均在低频kR< 0.5时取得，随着孔边裂纹数量的增加，其DSIF峰值逐渐增大，取得峰值时的频率逐渐向低频移动。随着无量纲波数的增加，孔边裂纹数量的影响逐渐减弱。

5　结　论

本文采用Green函数法、复变函数方法、裂纹“切割”技术和“契合”思想对压电材料中多个孔边径向裂纹在SH波作用下裂纹尖端的动应力强度因子问题进行了研究。主要结论如下：

(1) 在动态问题中，孔边径向裂纹尖端的DSIF值并不总是小于等效长度的直线型裂纹尖端的DSIF值。特别当裂纹长度与圆孔半径相差不大时，将孔边径向裂纹简化成直线型裂纹计算将引起明显误差，最高可达98%左右；

(2) 孔边径向裂纹尖端的DSIF值随入射波频率的增加振荡衰减，在低频段时DSIF曲线取得峰值，因此低频情况下的动力分析更为重要；

(3) 圆孔与裂纹尺寸、裂纹间距离及压电常数等都影响裂纹尖端的DSIF值。裂纹尺寸与圆孔半径为同一量级，裂纹间距离越小，压电常数越大，孔边径向裂纹尖端的DSIF峰值就越大；

(4) 圆孔边裂纹数目的增加会改变裂纹尖端的DSIF峰值，孔边裂纹数量越多，DSIF曲线峰值越大。

[1] 王保林. 压电材料及其结构的断裂力学[M]. 北京：国防工业出版社, 2003.

[2] 方岱宁, 刘金喜. 压电与铁电体的断裂力学[M]. 北京：清华大学出版社, 2008.

[3] 孔艳平, 田若萌, 刘金喜. 功能梯度压电层/压磁半空间结构中SH波传播[J]. 振动与冲击,2014,33(20):176-182.

KONG Yanping, TIAN Ruomeng, LIU Jinxi. Propagation of SH-waves in the structure of functionally graded piezoelectric layer/piezomagnetic half space [J]. Journal of Vibration and Shock, 2014, 33(20): 176-182.

[4] NARITA F, SHINDO Y. Dynamic anti-plane shear of a cracked piezoelectric ceramic [J]. Theoretical and Applied Fracture Mechanics, 1998, 29(3): 169-180.

[5] MEGUID S A, WANG X D. Dynamic antiplane behaviour of interacting cracks in a piezoelectric medium [J]. International Journal of Fracture, 1998, 91(4): 391-403.

[6] WANG X D, MEGUID S A. Modelling and analysis of the dynamic behaviour of piezoelectric materials containing interacting cracks [J]. Mechanics of Materials, 2000, 32: 723-737.

[7] WANG X D. On the dynamic behaviour of interacting interfacial cracks in piezoelectric media [J]. International Journal of Solids and Structures, 2001, 38: 815-831.

[8] 周振功, 王彪. 压电材料中两平行对称可导通裂纹断裂性能分析[J]. 应用数学和力学, 2002,23(12):1211-1219.

ZHOU Zhengong, WANG Biao. The behavior of two parallel symmetric permeable cracks in piezoelectric materials [J]. Applied Mathematics and Mechanics,2002,23(12):1211-1219.

[9] 周振功, 王彪. 压电材料中两个非对称平行裂纹的基本解[J]. 应用数学和力学, 2007, 28(4): 379-390.

ZHOU Zhengong, WANG Biao. Basic solution of two parallel non-symmetric permeable cracks in piezoelectric materials [J]. Applied Mathematics and Mechanics, 2007, 28(4): 379-390.

[11] WANG Y J, GAO C F. The mode III cracks originating from the edge of a circular hole in a piezoelectric solid [J]. International Journal of Solids and Structures, 2008, 45: 4590-4599.

[12] GUO J H, LU Z X, HAN H T, et al. Exact solutions for anti-plane problem of two asymmetrical edge cracks emanating from an elliptical hole in a piezoelectric material [J]. International Journal of Solids and Structures, 2009, 46: 3799-3809.

[13] GUO J H, LU Z X, HAN H T, et al. The behavior of two non-asymmetrical permeable cracks emanating from an elliptical hole in a piezoelectric solid [J]. European Journal of Mechanics A/Solids, 2009, 46: 3799-3809.

[14] 宋天舒, 李冬, 牛士强. 压电材料中孔边径向裂纹的动应力强度因子[J]. 工程力学, 2010, 27(9): 7-11.

SONG Tianshu, LI Dong, NIU Shiqiang. Dynamic stress intensity factor for radial cracks at the edge of a circular cavity in a piezoelectric medium [J]. Engineering Mechanics, 2010, 27(9): 7-11.

[15] 宋天舒, 李冬. 压电体中孔边III型界面裂纹的动应力强度因子[J]. 力学学报, 2010, 42(6): 1219-1224.

SONG Tianshu, LI Dong. Dynamic stress intensity factor for interfacial cracks of mode III on a circular cavity in piezoelectric bimaterials [J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1219-1224.

[16] 史守峡, 刘殿魁. SH波与界面多圆孔的散射及动应力集中[J]. 力学学报, 2001, 33(1): 60-70.

SHI Shouxia, LIU Diankui. Dynamic stress concentration and scattering of SH-wave by interface multiple circle canyons [J]. Chinese Journal of Theoretical and Applied Mechanics, 2001, 33(1): 60-70.

[17] 刘殿魁, 刘宏伟. 孔边裂纹对SH波的散射及其动应力强度因子[J]. 力学学报, 1999, 31(3): 292-299.

LIU Diankui, LIU Hongwei. Scattering of SH-wave by cracks originating at a circular hole edge and dynamic stress intensity factor [J]. Chinese Journal of Theoretical and Applied Mechanics, 1999, 31(3): 292-299.

[18] SIH G C. Stress distribution near internal crack tips for longitudinal shear problems [J]. Journal of Applied Mechanics, 1965, 32(1): 51-58.

Dynamic behaviors of interacting radial cracks at the edge of the circular cavities in piezoelectric medium

LI Dong1, WANG Huicong1, SONG Tianshu2

(1. Department of Civil Engineering, Hebei Jiaotong Vocational & Technical College, Shijiazhuang 050091, China;2. School of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China)

Based on the method of Green’s function, this work studied the interaction of the radial cracks emanating from the edges of the circular cavities in piezoelectric material, which was subjected to the dynamic incident anti-plane shearing wave(SH-wave). Firstly, coupled Green’s functions for displacement and electric potential were established by using a complex variable method. Secondly, crack-division technique was used to construct the model of radial cracks. The problem was reduced to a series of Fredholm integral equations of the first type according to the continuity conditions of the displacement and stress at the interface. Finally, numerical results were provided by solving the equations to show the influences of the geometry parameters, piezoelectric characteristic parameters, and the wave frequencies of incident wave on the dynamic stress intensity factors(DSIFs) at the crack tips.

piezoelectric medium; radial cracks emanating from the edge of the circular cavities; Green’s function; dynamic stress intensity factor(DSIF); SH-wave scattering

河北省教育厅青年自然科学基金项目(Q2012031)

2015-04-23修改稿收到日期：2015-08-12

李冬 男，博士，讲师，1983年9月生

O346.1

A

10.13465/j.cnki.jvs.2016.16.028