M/M/c型与M/M/1型排队系统对比仿真

孙 健，丁日佳1，陈艳艳3

（1.中国矿业大学（北京）管理学院，北京 100083；2.北京工业大学实验学院，北京 101101；3.北京工业大学交通工程北京市重点实验室，北京 100124）

M/M/c型与M/M/1型排队系统对比仿真

孙 健1，2，丁日佳1，陈艳艳3

（1.中国矿业大学（北京）管理学院，北京 100083；2.北京工业大学实验学院，北京 101101；3.北京工业大学交通工程北京市重点实验室，北京 100124）

为了更具体地分析M/M/c和c个M/M/1并联系统在性能上的差异，首先分析了Little公式在应用中可能存在的缺陷，然后通过AnyLogic仿真工具对模型运行过程进行跟踪，最后通过管理系统仿真（general purpose simulation system，GPSS）JAVA仿真获取了2种排队系统中服务台利用率、平均队长、最大队长、平均等待时间等对比指标，并指出了M/M/1并联系统用解析法求解存在的缺陷.仿真结果表明:2种排队系统中服务台利用率几乎相同；M/M/c系统中顾客平均等待时间稍短于c个M/M/1并联系统，对传统排队论中的“与c个M/M/1并联系统相比，M/M/c系统可以显著提高服务效率和减少等待时间”结论进行了修正.此外，M/M/c系统中“短时等待”顾客更多，其“零等待”顾客数和“长时等待”顾客数均显著少于c个M/M/1并联系统.

M/M/c排队；M/M/1排队；多Agent；管理系统仿真；排队论；AnyLogic

排队论（queuing theory），又称随机服务系统理论（random service system theory）.1909年由丹麦工程师爱尔朗（A.K.Erlang）在研究电话系统时创立.具体地说，它是在研究各种排队系统概率规律性的基础上，解决相应排队系统的最优设计和最优控制问题.随着计算机技术尤其是仿真技术的发展，排队论的应用有了更广阔的前景.

在机场、火车站等人流密集场所，顾客的到达受航班波、交通状况等诸多因素的影响，呈现出随机性、涌现性的特点，同时，枢纽内空间有限，增加服务台数量的余地不大，改变排队规则便成为诸多学者研究的重点.文献［1-4］分别从定性和定量角度研究了排队方式对系统性能的影响.文献［5］明确指出:“与直线型排队系统相比，折线型排队有更好的系统性能，可以提高服务效率和减少排队等待时间”，并给出了具体的对比数据.潘向东［6］指出:采用叫号机后（变直线型为折线型），银行服务系统的平均等待时长缩短了24.6％，过长等待的顾客数量减少了39.9％.王志清［7］指出:将5个值机柜台作为一个蛇形排队区，可使顾客平均等待时间缩短30％以上.以上学者基于Little公式计算了2种排队系统的性能对比指标，笔者认为其计算过程存在一定的缺陷.

本文主要研究在相同的顾客到达、相同服务台数目、遵循先到先服务规则的前提下，2种排队系统在性能上的差异.仿真研究发现，折线型排队方式并不能提高服务效率和显著缩短排队等待时间.本文首先分析了Little公式在求解并联M/M/ 1系统中可能存在的缺陷，然后通过AnyLogic仿真工具［8-9］对模型运行过程的细节进行了跟踪，最后，通过GPSSJAVA仿真工具获取了2种排队系统中服务台利用率、平均最长、最大队长、平均等待时间等数据.仿真的结果验证了本文的结论.

1 排队论经典算法的缺陷分析

［5］中有如下案例:某售票处有3个窗口，同时出售各车次的车票.顾客到达服从到达率为λ的泊松分布，服务时间服从服务率为μ的负指数分布，分2种情况［5］.

1）采用M/M/c型排队方式，顾客排成一队，依次购票（M/M/3/∞/∞），如图1（a）所示.

2）采用并联M/M/1型排队方式，顾客在每个窗口排1队，不准串队（3个M/M/1/∞/∞并联）.如图1（b）所示.

求:1）售票处空闲的概率.

2）平均等待时间和逗留时间.

3）队长和队列长.

排队方式1的计算过程如下:

售票处空闲概率

式中:Wq为顾客平均等待时间；Ws为顾客平均逗留时间；ρ=λ/μ.

经典排队论对排队方式2进行了简化处理，每个队列的到达率被修正为λ/3，然后按照M/M/1系统求解.

将λ=0.9、μ=0.4代入求解，结果如表1所示.

从表1各指标的对比可以看出:折线型排队比直线型排队有显著的优越性:服务台空闲率大大降低，顾客必须等待的概率降低18％，平均队列长降低24％，平均逗留时间为后者的一半.

文献［5］针对这个结论做了如下备注［5］:“相比之下，排1队共享3个服务台效率好.须注意，本例不允许串队，这是理论研究的要求，在实践中，若允许各排队顺序的前提下串队，实际效率相差不会这样大，但是差距肯定会有的，并且比较大.”可见，文献［5］中对表1中的结果表现出了一定的不确定性，笔者认为仅通过改变排队方式，系统性能不可能有如此大的提升.

经典排队论基于解析法求解，在一定程度上忽视了随机性因素对系统的影响，系统仿真的方法可以突破数学手段的限制，能够建立既表达系统物理特征又表达系统逻辑特征的模型，而且还可以很好地处理随机因素对系统的影响.针对上述问题，笔者基于AnyLogic和GPSS分别进行了仿真实验，以便对实验结果进行对比分析.

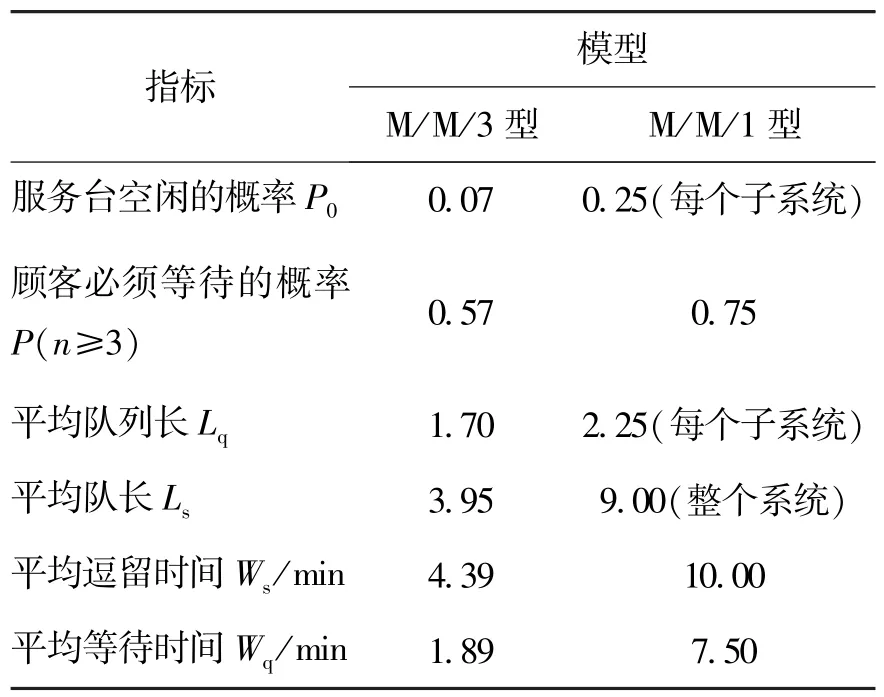
表1　2种排队系统性能指标对比表［5］Table 1 Performance indexes of the two queuing system［5］

2 基于多Agent模型的比较实验

多智能体系统是由多个相互独立的自治智能体构成的分布系统，他们处于相同的工作环境，能够感知环境信息并执行各自的行为动作［10］.将排队系统中的顾客和服务员分别封装为Agent，可以更准确地对M/M/c型和M/M/1型排队系统进行对比研究.图2是基于AnyLogic的2种排队系统的仿真模型.

在图2中，source模块用于产生顾客agent，delay模块用于模拟顾客接受服务所持续的随机时间（服务台的容量由对应的resourcePool定义），seize和release模块分别模拟顾客对服务台的占用和释放，sink模块表示顾客被排出模型，MaxQueue、MaxQ1、MaxQ2、MaxQ3分别记录模拟过程中各个队列的最大队长，系统还定义了事件event、event1和变量n.

2.1多Agent仿真模型的运行机制分析

仿真模型的步长等于相继到达的2个顾客的间隔时间.该间隔时间服从均值为1/0.9的指数分布（顾客到达率为0.9）.每个仿真步长开始的时刻，event事件被触发一次，系统会同时产生2个顾客分别进入子模型1和子模型2，由于子模型2中有3个source模块，event事件安排当前队长最短的那个source模块产生一个顾客，其余2个source模块不产生顾客.因此，通过event事件的处理机制，可以保证2个子模型有完全相同的顾客到达规律.

模型中变量n的初值为5 000，每当有顾客进入sink模块，n的值就减少1，当n为0时，事件event1被触发，模型停止运行.

2.2实时队长的对比分析

图3显示了在模拟过程中，从第1 160～1 660 min期间，M/M/c系统的队长和M/M/1系统中3个队长之和的实时对比情况，从图3可以得出如下结论:

在顾客到达的低峰期，M/M/c系统的当前队长低于M/M/1系统中3个队长之和；在顾客到达的高峰期，M/M/c系统的当前队长高于M/M/1系统中3个队长之和.

从图3可以看出，在第1 200～1 260 min期间，M/M/c系统的队长保持在0左右，而M/M/1系统中3个队长之和保持在5以上，最高值为14.笔者认为这种现象是由服务时间的不均匀性造成的，由于不许串队，在M/M/1系统中，即使相邻的服务台空闲，顾客也只能在队列中等待.由于以上2个系统的服务时间均服从指数分布，因而可以认定，在顾客到达低峰期，M/M/c系统服务台利用效率高，顾客排队等待时间短.

在服务高峰时段，如第1 460～1 660 min期间，M/M/c系统的队长远高于M/M/1系统中3个队长之和.甚至在M/M/1系统中3个队长之和很小（小于3）的时候，M/M/c系统队长仍然在5以上，甚至高达24.同低峰期一样，这也是由指数分布的不均匀性造成的.

2.3仿真结果的对比分析

上述模型启动后，当时钟推进到第5 547.02 min时，第5 000名顾客流入子模型2的sink模块，模拟结束.仿真结果如表2所示.

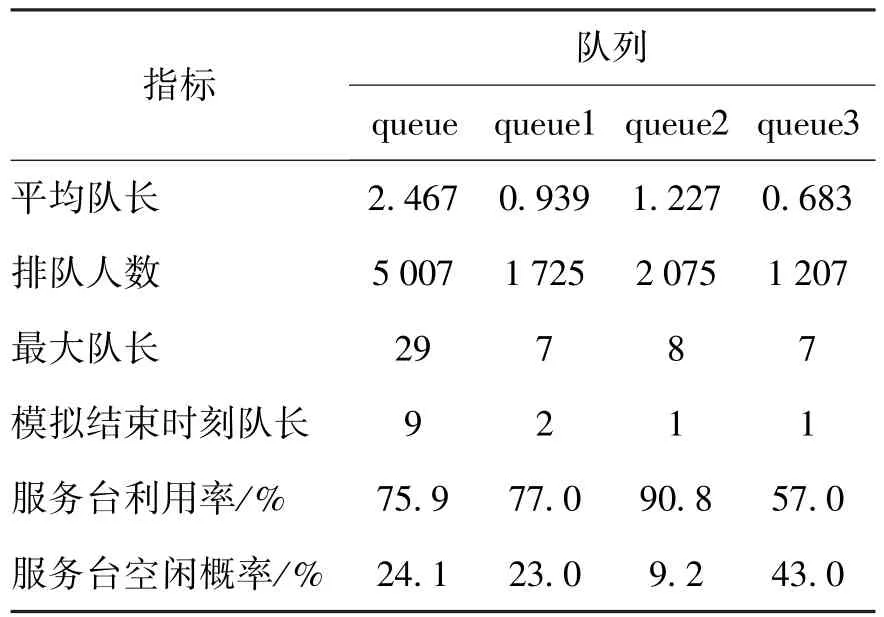
表2　基于仿真法的系统性能指标对比表Table 2 Simulation performance of the two systems

以模拟期间各队列排队人数为权重，并联M/ M/1系统平均队长加权值为0.997，略高于M/M/c系统平均队长除以3的值0.822 3；并联M/M/1系统服务台利用率加权值77.9％，略高于M/M/c系统的75.9％.

3 基于随机因素的理论分析

3.1Little公式的适用性分析

图1（b）中，到达率为λ的泊松流被简化为3个λ/3的泊松流，可能是造成计算结果差异的主要原因.因为爱尔朗分布也用来表示独立随机事件发生的时间间隔，如果λ=0.9的泊松顾客流被依次分配到3个服务台，对单个服务台来讲，顾客到达间隔时间被拉长，这符合爱尔朗分布的定义:“设V1，V2，…，Vk相互独立，Vi～E（0，kμ），则T=V1+ V2+…+Vk，则T服从k阶爱尔朗分布.”因为指数分布随机数流合并后形成的是爱尔朗分布.顾客以λ=0.9的到达率进入系统后，假设第1位、第3+1位、第6+1位……顾客进入1号服务台，第2位、第3+2位、第6+2位……顾客进入2号服务台，第3位、第3+3位、第6+3位……顾客进入3号服务台接受服务的话，3个服务台顾客到达均服从3阶的爱尔朗分布，即演变成为3个E3/M/1并联的排队系统.由于爱尔朗分布不具备马尔科夫性，因此不能再用Little公式求解.

3.2M/M/1与M/M/c系统优缺点分析

指数分布与爱尔朗分布的关系如图4所示.

当k=1时，爱尔朗分布化为负指数分布，可看成是一种完全随机的分布；

当k增大时，爱尔朗分布的图形逐渐变为对称的；

当k≥30时，爱尔朗分布近似于正态分布；

k→∞时，Var［T］→0，这时爱尔朗分布化为确定型分布.

排队论研究的内容是如何构建一个系统，使之对顾客和服务员均有利，对于管理当局来讲，理想的排队系统应该是降低排队长度，提高服务员利用率.

1）以排队长度为研究对象

排队长度与顾客到达流密切相关，将M/M/c型排队系统变更为c个M/M/1并联系统，可以使指数分布的到达流演变成为c个c阶分布的爱尔朗流，并且，随着c的增大，顾客到达间隔时间的离散性有进一步减少的趋势，因此，可以认为，M/M/c型排队系统可以有效抵消短时大客流对服务系统造成的冲击.

2）以服务员利用率为研究对象

在M/M/c系统中，一个队列对应多个服务台，相当于将服务时间由指数分布转化为c阶爱尔朗分布，因此，在客流到达低峰时期，可以有效提高服务台利用率，如果在客流到达高峰期，所有服务台均满负荷运作，二者服务员利用率均为100％.

综上所述，并联M/M/1系统将顾客加入队列的间隔时间由指数分布转变为爱尔朗分布，可以有效抵消短时大客流对于服务系统的冲击；M/M/c系统将顾客离开队列到达服务台的时间间隔由指数分布转变为爱尔朗分布，可以有效提高服务台在低峰时期的利用率.

以上是基于AnyLogic仿真平台的2种排队系统对比分析，由于AnyLogic是商业软件，对其内部调度程序、仿真步长机制等做了封装，无法求解系统中顾客的平均等待时间（每位顾客等待时间之和/顾客数），因此，本文采用笔者参与开发的GPSS/JAVA再次建立2种排队系统的对比分析模型.

4 基于GPSSJAVA仿真模型的对比实验

4.1建模过程分析

图5（b）展示了折线型排队的GPSS模型，该模型定义了一个队列q1，一个并行服务能力为3的服务实体s1.顾客在generate模块的作用下，通过2号随机数发生器产生到达间隔均值为1/λ的指数分布随机数流，用以模拟顾客的到达，顾客进入系统后，首先排入队列s1，在队列中试图占用其中一个空闲的服务台，如果能够占用，就离开队列，进入advance模块，滞留时间是指数分布（均值2.5 min）的一个抽样值，滞留期满后，离开advance模块，进入leave模块，释放其所占用的服务员，进入terminate模块，被排出模型，同时使模拟终止计数器减1（模拟终止计数器初值为5 000，计数器值为0时，模型运行结束）.

图5（a）展示了直线型排队GPSS模型，在该模型中，首先创建3个单服务台实体f1、f2、f3，然后创建3个队列对象q1、q2、q3，定义了3个QTable类的对象用于分别计算顾客在3个队列中等待时间的均值和标准差等数据.顾客经generate模块进入系统后，第1个select语句的作用是从1～3号服务台中选取当前空闲的服务台，并将其编号存入该顾客的1号参数，如果3个服务台都忙，则其1号参数值为0，接下来的test模块就是比较该顾客1号参数P$（1）的值是否为0，如果为0，说明该顾客到达时，3个服务台均处于忙态，于是该顾客进入紧后的select模块，在该模块中，寻找当前队长最短的队列，并将该队列的编号存入其1号参数中，然后通过queue模块排入1号参数所对应的队列；如果该顾客的1号参数值不为0，说明该顾客到达时，至少有一个服务台处于闲态，于是该顾客直接进入地址标号为zeroArrival的模块，即排入其1号参数所对应的队列（QP（1）返回当前顾客1号参数所对应的队列对象，FP（1）返回1号参数对应的服务台对象）.然后在队列中试图占用该队列对应的服务台，如果能够占用就离开队列，进入advance模块，服务完成后，通过release模块释放所占用的服务员，进入terminate模块被排出模型.

4.2模拟结果的对比分析

M/M/3排队模型服务完第5 000位顾客后，模拟结束，历时5 526.8 min，其服务台利用率为76.0％；折线型排队系统在稳态下服务5 000位顾客历时5 527.1 min，在直线排队模型中，3个服务台的忙闲率分别为85.8％、76.4％和65.8％，加权平均忙闲率为76.69％，此结果与基于AnyLogic的计算结果基本一致，其差异可能是2种仿真工具随机数生成算法的不同造成的.

表3列出了2种系统中与队列有关的统计数据，M/M/1型（以下称直线型）系统中，有更多的顾客能得到“零等待”服务（“零等待”指顾客到达时，服务台正好空闲，顾客排队时间为0），但其顾客的平均等待时间长于M/M/c型（以下称折线型）系统.对表2中的平均等待时间求加权平均，直线型为2.422 7 min（加权平均），折线型为2.012 3 min；摒除所有“零等待”顾客，“非零等待”顾客的平均等待时间，直线型为4.583 4 min，折线型为3.522 9 min，见表3.

表3　排队性能指标对比（模拟5 000位顾客服务过程）Table 3 Contrast of performance index（for 5 000 customers）

表3展示了模拟结束时，2个系统中队列的排队统计情况，从表3可以看出，无论是所有顾客的平均等待时间还是“非零等待”顾客的平均等待时间，折线型排队系统均优于直线型排队系统，但二者差别并不大.

表4统计了所有顾客排队等待时间的分布情况，从表4可以看出，等待时间为0的顾客数，直线型排队系统比折线型多222人，但是，在等待时间为0～7 min的区间内，折线型排队系统的人数比直线型多462人，在等待时间为7～21 min的区间内，折线型排队系统的人数比直线型少240人.于是得出以下3条结论（如图6所示）:

1）零等待顾客数，直线型排队比折线型多5％左右.

2）在等待时间0～7 min区间内的顾客数，直线型排队比折线型少10％左右.

3）在等待时间7～21 min区间内的顾客数，直线型排队比折线型多5％左右.

也就是说，在直线型排队系统中，顾客“零等待”的概率稍高，但是短时等待（0～7 min）的顾客明显少于折线型，而长时等待（7～21 min）的顾客又明显多于折线型.从排队顾客的平均等待时间上来看，直线型为2.422 7 min，折线型为2.012 3 min；“非零等待”顾客的平均等待时间，直线型为4.583 4 min，折线型为3.522 9 min，本例中，在“零等待人数”方面，直线型排队系统有2 385人，占比48％，折线型排队系统仅为43％；直线型比折线型高出5个百分点，在短时等待（0～7 min）人数方面，折线型排队系统有2 519人，占比51％，直线型排队系统有2 057人，占比41％，直线型比折线型低10个百分点，在长时等待（7～21 min）方面，折线型排队系统为558人，占比11％，而折线型排队系统仅有318人，占比6％，仅为前者的一半左右（比直线型低5个百分点），因此，归纳出的结论是，折线型排队系统顾客等待时间更加均匀，在顾客平均等待时间比直线型排队系统稍短.

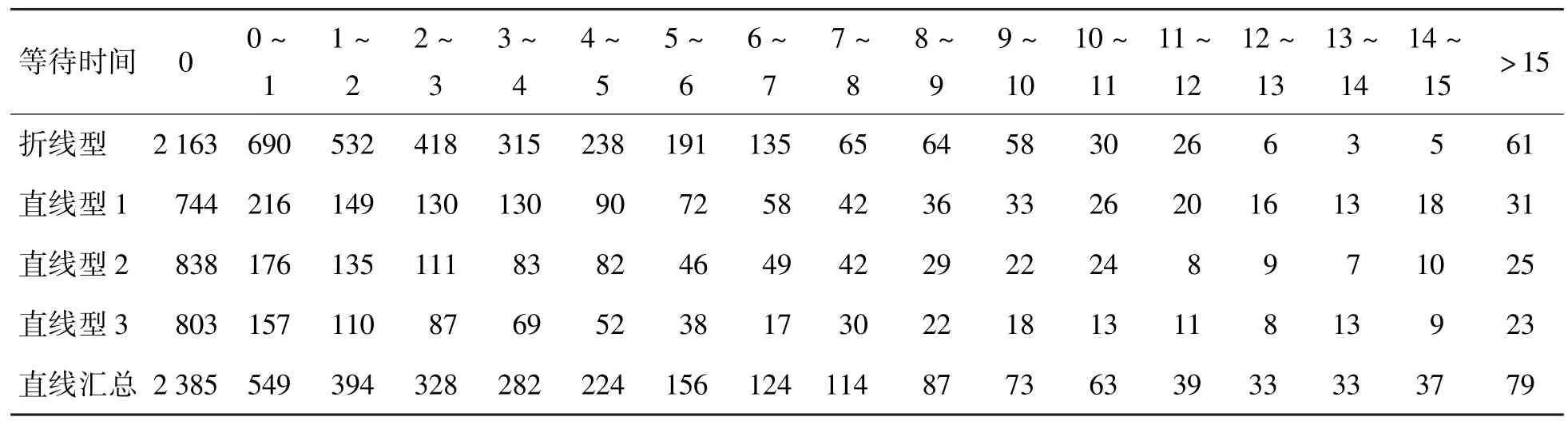
表4　M/M/3型和3个M/M/1型并联系统排队人数与等待时间对应关系表Table 4 Waiting time collection table of the two queuing systemmin

如果把模拟时长增加1倍，在稳态下模拟50 000名顾客接受服务的过程，会发现直线型和折线型排队系统的统计性能没有太大的变化，这也验证了在系统进入稳态的情况下，队长的分布、等待时间的分布和忙期的分布都和系统所处的时刻无关，而且系统的初始状态的影响也会消失.

5 结论

本文分别运用解析法、多Agent仿真工具、GPSS仿真工具对M/M/1和M/M/c排队系统进行了求解，并对2种系统的排队性能指标进行了对比分析.本文所研究排队系统的服务强度ρ＜1，系统不可能出现队列无限长的情况，但是顾客到达和服务时间的随机性，造成了系统在某个阶段队列较长，而另外一些时候服务员（台）又空闲无事.因此，随机性因素是造成排队现象的主要原因.本文分析了基于解析法求解的排队论理论在实际应用中存在的缺陷，通过基于AnyLogic的仿真得出以下结论:

1）M/M/3系统的平均队长为2.467，服务台空闲率为24.1％；并联M/M/1系统中加权平均队长为0.997，服务台加权平均空闲率为22.1％，2种排队系统整体性能相差不大.

2）在旅客到达低峰期，M/M/c系统当前队长显著小于并联M/M/1系统3个队长之和，在旅客到达高峰期，M/M/c系统当前队长显著大于并联M/ M/1系统3个队长之和.并联M/M/1系统可以有效降低大客流对于服务系统的冲击；M/M/c系统会造成服务员在闲的时候更闲，在忙的时候更忙.

通过基于GPSS/JAVA的仿真模型可以得出以下结论:

1）与基于Anylogic模型的计算结果基本一致，可以互相印证其合理性.

2）M/M/c系统中“短时等待”顾客更多，其“零等待”顾客数和“长时等待”顾客数均显著少于c个M/M/1并联系统.

“与c个M/M/1并联系统相比，M/M/c系统可以显著提高服务效率和减少等待时间”是文献［5］的经典结论，本文仅通过仿真的方法，对2种排队系统进行了实证研究，得出的结论是:与M/M/c系统相比，M/M/1系统将指数分布的顾客到达流转化为爱尔朗分布的到达流，可有效降低高峰时期的排队队长；M/M/c系统将指数分布的服务时间转化为爱尔朗分布的服务时间，可以使服务员利用率更加均匀，但2种排队系统整体性能相差不大.

本文在仿真建模和计算过程中可能还存在一定考虑不周的地方，本文在此抛砖引玉，也希望能有更多的学者对此问题进行更进一步的研究.

参考文献：

［1］KALASHNIKOV V V.Mathematical methods in queuing theory［M］.Berlin:Springer Science＆amp;Business Media，2013.

［2］周文慧，黄伟祥.提高顾客等待满意度的两类排队管理策略［J］.管理科学学报，2014，17（4）:1-10. ZHOU W H，HUANG W X.Two kinds of queuing management policy for improving customer satisfaction with waiting［J］.Journal of Management Sciences in China，2014，17（4）:1-10.（in Chinese）

［3］叶峰，赵秋红，闪四清.基于仿真模型的排队规则遗传优化算法研究［J］.系统工程理论与实践，2013，33 （8）:2080-2086. YE F，ZHAO Q H，SHAN S Q.Research on genetic otimization algorithm of queue rules based on simulaton model［J］.Systems Engineering-Theory＆amp;Prictice，2013，33（8）:2080-2086.（in Chinese）

［4］明朝辉，韩松臣.PBN下多跑道机场航班起降运行排队方式研究［J］.数学的实践与认识，2011，41（20）: 143-148. MING Z H，HAN S C.Queuing way system of the multirunway airport flight operation of PBN［J］.Mathematics in Practice and Theory，2011，41（20）:143-148.（in Chinese）

［5］胡运权.运筹学基础及应用［M］.5版.北京:清华大学出版社，2013.

［6］潘向东.银行排队系统服务效率问题研究［J］.技术经济与管理研究，2009（4）:73-75. PAN X D.Research about service efficiency of bank queuing system［J］.Technoeconomics＆amp;Management Research，2009（4）:73-75.（in Chinese）

［7］王志清.民航旅客运输便捷工程及其流程优化方法研究［D］.南京:南京航空航天大学，2006. WANG Z Q.Research on the convenient engineering of air transportation and its process optimization［D］.Nanjing: Nanjing University of Aeronautics and Astronautics，2006. （in Chinese）

［8］任毅，孙健.管理系统仿真与GPSSJAVA［M］.北京:清华大学出版社，2009.

［9］孙健，丁日佳.Web版GPSS/JAVA运行机制的研究与实践［C］∥系统仿真技术与应用（13卷）.华盛顿:美国科研出版社，2011:395-399. SUN J，DING R J.Researchs on running mechanism of GPSS/JAVA Webedition［C］∥SystemSimulation Technology＆amp;Application（Volume 13）.Washington: Scientific ResearchPublishing，2011:395-399.（in Chinese）

［10］段勇.基于多智能体强化学习的多机器人协作策略研究［J］.系统工程理论与实践，2014，34（5）:1305-1310. DUAN Y.Research on multi-robot cooperation strategy strategy based on multi-agent reinforcement learning［J］. Systems Engineering—Theory＆amp;Practice，2014，34（5）: 1305-1310.（in Chinese）

（责任编辑 吕小红）

Comparative Simulation on M/M/c and M/M/1 Queuing Systems

SUN Jian1，2，DING Rijia2，CHEN Yanyan3
（1.Management Institute，China University of Mining and Technology（Beijing），Beijing 100083，China；2.Experimental Institute，Beijing University of Technology，Beijing 101101，China；3.Beijing Key Laboratory of Traffic Engineering，Beijing University of Technology，Beijing 100124，China）

To make a more detailed analysis of the differences in performance between M/M/c and M/M/ 1 c parallel systems，in this paper，first，the possible defects in the application of Little formula were analyzed.And then the running process of the model was tracked by AnyLogic.Finally，the service desk utilization，average queue length，maximum queue length，average waiting time of the two queuing system by GPSSJAVA were obtained.The defects of the analytical method for the M/M/1 parallel system were identified.Simulation results show that the service desk utilization is almost identical to the two queuing systems.The average waiting time of customers in M/M/c system is slightly shorter than that of c parallel M/M/1 system.And the classic conclusion of“compared with the c M/M/1 parallel system，M/ M/c system can significantly improve the service efficiency and reduce the waiting time”conclusion was revised，Moreover，M/M/c system has more short term waiting customers，its zero waiting and long waiting customers are significantly less than that in c M/M/1 parallel system.

M/M/c queue；M/M/1 queue；multi-Agent；general purpose simulation system（GPSS）；queue theory；AnyLogic

C 93；TP 308

A

0254-0037（2016）09-1324-08

10.11936/bjutxb2015120042

2015-12-17

北京市自然科学基金重点资助项目（8131001）

孙 健（1979—），男，讲师，主要从事离散系统建模与仿真方面的研究，E-mail:gzsunjian@bjut.edu.cn