基于粒子群优化的溶解氧质量浓度支持向量回归机

安爱民，祁丽春，丑永新，张浩琛，宋厚彬

（兰州理工大学电气工程与信息工程学院，兰州 730050）

基于粒子群优化的溶解氧质量浓度支持向量回归机

安爱民，祁丽春，丑永新，张浩琛，宋厚彬

（兰州理工大学电气工程与信息工程学院，兰州 730050）

针对污水处理中溶解氧质量浓度无法在线精确测量的问题，提出基于粒子群算法优化支持向量回归机（PSO-SVR）的溶解氧质量浓度软测量模型.为了提高溶解氧的预测精度和效率，采用粒子群算法对支持向量回归机的模型参数进行优化，并以自动获取的最佳参数组合构建溶解氧与其影响因子间的非线性软测量模型，利用该软测量模型对国际基准仿真模型BSM1的溶解氧质量浓度进行预测.仿真结果表明:该模型能得到较好的预测效果，与SVR、RBF神经网络相比，PSO-SVR模型不仅计算复杂度低，而且收敛速度快，预测精度高，泛化能力强.

溶解氧质量浓度；粒子群算法；支持向量回归机；污水处理；软测量

在污水处理的过程中，污水成分繁杂多变，且污水和污泥流量中存在许多不确定因素，导致污水处理系统中的溶解氧质量浓度的测量存在时变和滞后大、易被干扰等缺陷.溶解氧质量浓度与进水量和生化池组分质量浓度之间具有十分密切的关联，在污水处理系统中，溶解氧质量浓度的准确预测和系统动态特性描述是目前亟待解决的问题［1］.软测量技术［2-3］是解决该问题的有效方法之一，可作为仪表测量的辅助，降低污水处理系统的总体成本，已在污水处理领域得到了一定关注.

Oscar等［4］采用离散扩展卡尔曼滤波，基于污水处理系统中曝气池溶解氧（dissolved oxygen，DO）质量浓度和空气流量，对污水处理机理模型中的呼吸速率和曝气的传质系数进行预测，实现了这2个变量的软测量.Aguado等［5］采用软测量方法对SBR工艺各阶段的处理时间进行最优预测，通过对不同工艺阶段的分时控制，克服了传统SBR工艺中各阶段处理时长固定的缺陷，对整个SBR工艺进行了优化.Xie等［6］采用混合建模方法建立了直流蒸汽发生器中蒸汽的软测量模型，提高了模型的泛化能力，成功运用于蒸汽发生器中蒸汽量的预测.

粒子群算法具有收敛速度快、占用系统资源少等优点［7］，本文提出了基于粒子群算法（particle swarm optimization，PSO）优化支持向量回归机的溶解氧软测量模型，通过粒子群优化算法对支持向量回归机的模型参数进行优化，以最佳参数组合构建污水处理系统进水参数与溶解氧之间的非线性关系模型.将该模型用于国际基准仿真模型BSM1溶解氧质量浓度的预测，与支持向量回归机（support vector regressor，SVR）和RBF神经网络的预测结果作对比分析，仿真结果表明，所建立软测量模型具有预测精度高和计算效率好的优点.

1 活性污泥法优化控制系统

欧盟科学技术与合作组织与国际水质协会携手开发了活性污泥污水处理基准仿真模型（BSM1），用于污水处理系统中一些控制方法的性能评价. BSM1的总体布局如图1所示，系统包括的生化池和二沉池，其容积都为6 000 m3.其中生化池由5个部分组成，前2个部分为厌氧区，后3个部分为好氧区［1］.生化池的反应机理以国际水质协会提出的活性污泥1号ASM1模型为基础，模拟其反应过程；二沉池由10层组成，基于二次指数沉淀速率模型，模拟其沉淀过程.

在整个污水处理动态系统中，影响溶解氧质量浓度的因素有很多且相对复杂，包括微生物以及有机物等物质质量浓度，溶解氧质量浓度SO用数学模型表示为

式中:μH为异养菌最大生长速率；KOH为异养菌氧呼吸半速率常数；KS为异养菌生长半速率常数；μA为自养菌最大比生长速率；KNH为自养菌生长半速率常数；YH为异养菌产率系数；YA为自养菌产率系数.

2 基于粒子群优化的支持向量回归机

2.1支持向量回归机描述

支持向量机（support vector machine，SVM）是一种比较常用的软测量建模方法［8-9］.以结构风险最小化为基础，即使在小样本情况下，SVM也能得到最优预测结果，相比于常用的机器学习方法，其模型泛化能力强，易得到推广.

SVM为了解决分类问题而提出，Vapnik等［10］将不敏感损失系数引入SVM，使其可用于回归拟合，从而出现了SVR，在系统建模方面得到广泛应用.其原理如下:

设训练集样本对为｛（xi，yi），i=1，2，…，l｝，其中，l为训练集样本个数，xi为第i个输入向量，yi为xi对应的输出值.

定义ε线性不敏感损失函数为

式中:f（x）为SVR的预测值；y为对应的真实值.

回归函数为

式中:只有部分参数（αi-α*i）不为零，其对应的样本xi为支持向量.K（xi，x）=φ（x）φ（xi）称为核函数，本文核函数选用径向基函数（RBF），K（xi，xj）= exp（-‖xi-xj‖2/2δ2）.

图2可以看出，SVR的结构与神经网络的结构较为类似.输出是中间点的线性组合，每个中间节点对应一个支持向量.

在实际应用中，需要正确设置影响SVR算法性能的2个关键参数:惩罚参数C和核函数δ.本文利用粒子群算法优化SVR的惩罚参数和核函数.

2.2粒子群算法

由于粒子群算法简单、所需参数设置少以及易于实现等优点［7］，粒子群算法已得到了广泛应用.

粒子是粒子群算法中的基本组成单位，分别对应解空间的每个解.同时，粒子群的迁移过程不是无序的，具有一定的方向性，并在搜索过程中运用反馈原理和并行计算，达到较高的搜索速率.如果解向量为d维，且算法迭代次数为t，那么第i个粒子可表示为xi（t）=［xi1（t），xi2（t），…，xid（t）］.其中，xiq（t）代表第i个粒子在第q维解空间的位置，即第i个解中的第q个待优化变量.

在粒子群算法中，粒子的方向和速度由速度向量决定，粒子在寻优空间中的位置表示可行解.当处于初始状态时，在解空间中随机分布着每个粒子，它们随时可以根据极值来调整自己的位置和飞行速度.

粒子群算法更新方程为

图3所示为基于粒子群算法的支持向量回归机参数优化流程图.

3 溶解氧软测量模型

3.1溶解氧质量浓度软测量建模

为了更精确地建立溶解氧浓度软测量模型，首先要对影响溶解氧质量浓度的因素进行深入的分析，以避免建模过程变量信息不完备而降低模型的精度.

影响溶解氧质量浓度的因素有很多，需要对变量进行选取.模型输入变量的确定主要依据工艺机理和经验知识.模型建立步骤如图4所示，通过对污水处理的机理和操作特性进行分析，最终确定了6个输入变量:生化需氧量、化学需氧量、固体悬浮物、总氮、总磷的质量浓度，以及进水流量.模型输出为溶解氧质量浓度，共采取了500组数据，随机选取300组数据（总数据的2/3）作为训练数据，剩下的200组数据（总数据的1/3）作为模型泛化数据.

基于粒子群优化支持向量回归机的溶解氧软测量建模步骤如下:

步骤1 对初始仿真数据进行异常值检测与归一化处理，组成样本训练集和测试集；

步骤2 初始化SVR模型和粒子群算法的各参数，包括粒子群的初始参数c1和c2，初始速度矩阵v以及每个初始粒子个体最优位置pi和全局最优位置gi等，用训练样本集构建SVR回归估计模型；

步骤4 根据所得粒子的适应度函数值调整粒子个体最优位置pi和全局最优位置gi；

步骤5 根据式（4）（5）对粒子的状态进行更新，从而获得SVR的最佳参数组合；

步骤6 将求得的参数代入式（3），得到SVR的回归估计函数表达式，对未来某一时刻的溶解氧质量浓度进行预测.

3.2数据预处理

3.2.1异常值检测方法

由于操作不当、系统故障等原因，所采用的数据中会出现异常值，大大干扰模型的预测，难以准确得到其预测性能评价.为了解决这个问题，必须对异常值进行在线检测和排除，实现模型的无偏差正常运行［11］.

平时采用的异常值检测方法为3δ准则，但是此种方法已被证明效果并不理想，因为其均值和标准差易受到异常值的干扰，产生较大偏差.基于此，本文采用一种更具有鲁棒性的异常值检测方法，将均值和标准差用中值（Med）和中值绝对偏差（MAD）来替代［12］.设一组测量序列为x:｛x（t），t= 1，2，…，L｝，假如其中

则x（t）将被辨识为异常值.

如果满足式（6）而不满足式（8），在本文中就会被定义为中度异常值；但如果满足式（8），就会被定义为严重异常值；其余的称之为正常值.

3.2.2归一化操作

污水处理的入水参数之间存在不同的属性，受到许多不确定因素的影响，因此在建立溶解氧软测量模型之前，需对入水数据作归一化处理，加快训练网络的收敛性.

首先，令某组数据中最大值为Xmax，最小值为Xmin，则归一化前该组数据中的数据X在归一化后的值为

显然，要想获得其在原物理空间的数值，必须将网络输出进行反归一化

3.3性能评价

通过计算预测值与真实值误差判断PSO-SVR、SVR和RBF神经网络的泛化能力.本文选用的性能指标为相对误差（Ei）、均方根误差（RMSE）、相对均方误差均值（MSRE）、平均绝对误差（MAE）和决定系数（R2），其计算公式分别为

式中:^yi（i=1，…，n）为第i个样品的预测值；yi（i= 1，…，n）为第i个样品的真实值；n为样品的数目.

4 仿真结果与分析

为了测试粒子群算法优化支持向量回归机后溶解氧软测量模型的性能，入水流量数据共选取不同天气下7 d的综合数据，分别为干燥天气的第2、4、6天的数据，雨天第3、5天的数据，以及暴雨天第7、8天的数据，其中干燥天气第2天和雨天第3天这2 d的数据进行验证模型的输出，其他5 d的数据进行溶解氧软测量模型的训练.

针对所建的粒子群规模n=200，取c1=c2=2，r1和r2选取［0，1］的独立随机数，最大迭代次数取为45.通过粒子群算法对SVR参数组合寻优，其目标函数F值收敛曲线如图5所示，最后获得SVR最佳参数组合，将最佳参数组合代入PSO-SVR软测量模型中进行溶解氧质量浓度预测.

利用MATLAB仿真软件，并结合软件内部分工具箱，对模型进行仿真.仿真结果如图6～9所示.

图6～8分别是真实值与PSO-SVR、RBF、SVR的预测结果对比图，展示了3种方法各自对溶解氧质量浓度的预测精度情况.

从图9可以看出，PSO-SVR能较准地预测出生物池内溶解氧质量浓度值，与真实值的对比曲线几乎重合，说明该方法能够精确地利用进水参数预测出溶解氧质量浓度.而RBF神经网络和SVR在前90个样本中预测精度较高，但从第96个预测样本以后，拟合效果出现了较大误差，后半部分总体上比PSO-SVR的拟合效果差.

通过图10可以得到，粒子群算法优化后的支持向量回归机的相对误差明显小于RBF神经网络和未经优化的支持向量回归机.均方根误差、相对均方误差均值、平均绝对误差和决定系数如表1所示.

从表1可以看到，PSO-SVR的均方根误差、相对均方误差均值、平均绝对误差均小于RBF神经网络和SVR，同时，PSO-SVR的决定系数为0.9997，而RBF神经网络和SVR的决定系数为0.545 7和0.990 7，所以，PSO-SVR的模型性能更好，预测精度更高.

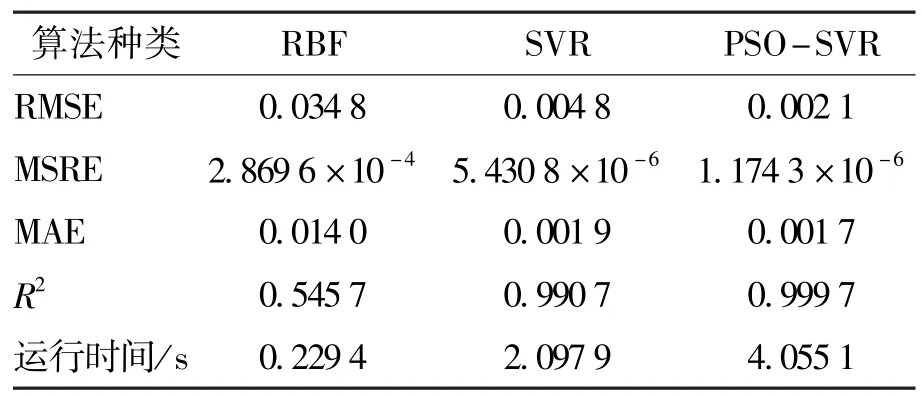
表1　各模型预测精度对比Table 1 Forecast accuracy of each model

5 结论

1）针对以往溶解氧预测方法存在的计算复杂度高、易陷于局部最优值和过学习等缺陷，提出了采用粒子群算法对支持向量回归机的参数组合进行优化选择的方法，构建了粒子群优化支持向量回归机的溶解氧软测量模型，进行了仿真实验和对比.

2）在相同的实验环境下，与RBF神经网络和SVR这2种预测方法进行对比，本文提出的PSOSVR预测模型各项评价指标均优于RBF和SVR这2种预测模型，预测误差更小.

3）将粒子群算法与支持向量回归机相融合，实现了支持向量回归机最佳参数的自动获取，大大提高了模型的预测精度.但与此同时，不可忽略的是PSO-SVR运行时间变长，因增加了粒子群的优化，相对地延长了模型预测的运行时间.

4）在今后的研究中需进一步探讨如何利用软测量方法提升模型预测的运行效率以及如何更快、更精确地获取最优的模型参数组合.

［1］韩广，乔俊飞，薄迎春.溶解氧浓度的前馈神经网络建模控制方法［J］.控制理论与应用，2013，30（5）:585-591. HAN G，QIAO J F，BO Y C.Feed forward neural network modeling and control for dissolved oxygen concentration ［J］.Control Theory＆amp;Applications，2013，30（5）:585-591.（in Chinese）

［2］张昭昭.污水处理过程出水水质多模型在线软测量方法［J］.控制工程，2014，21（1）:88. ZHANG Z Z.An online multi-model softsensing method of water quality in wastewater treatment process［J］.Control Engineering of China，2014，21（1）:88.（in Chinese）

［3］黄道平，刘乙奇，李艳.软测量在污水处理过程中的研究与应用［J］.化工学报，2011，62（1）:1-9. HUANG D P，LIU Y Q，LI Y.Soft sensor research and its application in wastewater treatment［J］.Journalof Chemical Industry and Engineering，2011，62（1）:1-9. （in Chinese）

［4］OSCAR A I S，PARK S W，GARCIA C.Software sensor for on-line estimation of the microbial activity in activated sludge systems［J］.ISA Transactions，2002，41（2）: 127-143.

［5］AGUADO D，RIBESJ，MONTOYAT，etal.A methodology for sequencing batch reactor identification with artificial neural networks:a case study［J］.Computers＆amp; Chemical Engineering，2009，33（2）:465-472.

［6］XIE L，ZHAO Y，AZIZ D，et al.Soft sensors for online steam quality measurements of OTSGs［J］.Journal of Process Control，2013，23（7）:990-1000.

［7］毕娅.云物流下基于协同库存和覆盖的选址-分配问题研究［D］.武汉:武汉理工大学，2012. BI Y.The location-allocation problem research in cloud logistics based on collaborative inventory and coverin［D］. Wuhan:Wuhan University of Technology，2012.（in Chinese）

［8］俞金寿.软测量技术及其应用［J］.自动化仪表，2008，29（1）:1-7. YU J S.Soft-sensing technique and its applications［J］. Process Automation Instrumentation，2008，29（1）:1-7. （in Chinese）

［9］杨慧中，贾淑矿.基于二次判别分析的多模型建模方法［J］.控制工程，2010，17（5）:662-664. YANG H Z，JIA S K.Multi-model modeling method based on quadratic discriminant analysis［J］.Control Engineering of China，2010，17（5）:662-664.（in Chinese）

［10］VAPNIK V，VAPNIK V.Statistical learning theory［M］. New York:Willey，1998:116-134.

［11］谢莉.非均匀采样数据系统的辨识及其应用研究［D］.无锡:江南大学，2013. XIE L.Identification anditsapplicationsfornonuniformly sampled-data systems［D］.Wuxi:Jiangnan University，2013.（in Chinese）

［12］QIAO J H，CHAI T Y.Soft measurement model and its application in raw meal calcination process［J］.Journal of Process Control，2012，22（1）:344-351.

（责任编辑 吕小红）

Support Vector Regression Using Particle Swarm Optimization for Dissolved Oxygen Concentration

AN Aimin，QI Lichun，CHOU Yongxin，ZHANG Haochen，SONG Houbin
（College of Electrical and Information Engineering，Lanzhou University of Technology，Lanzhou，730050，China）

To improve the precision and efficiency of dissolved oxygen，a particle swarm optimization （PSO）of support vector regression（SVR）method was proposed to predict the concentration of dissolved oxygen in the soft measurement model because of the problem of the dissolved oxygen concentration cannot be measured online in the wastewater treatment.The particle swarm algorithm was used to optimize the parameters of support vector regression，and the construction of dissolved oxygen and its impact factors in nonlinear soft sensor prediction model were automatically obtained by the best combination of parameters by using the model of dissolved oxygen concentration on the international BSM1 benchmark simulation model.The simulation shows that the prediction model has good prediction effect compared with SVR，RBF neural network model，the PSO-SVR model not only has low computational complexity，but also has the advantages of fast convergence，high forecast precision，strong generalization ability etc.

dissolved oxygen concentration；particle swarm algorithm；support vector regressor；wastewater treatment；soft sensor

TQ 015.9；TP 391.9；O 6-39

A

0254-0037（2016）09-1318-06

10.11936/bjutxb2015120041

2015-12-17

国家自然科学基金资助项目（61563032）

安爱民（1972—），男，教授，主要从事工业过程先进控制技术方面的研究，E-mail:anaiminll@163.com