有理三角 Bézier曲线曲面光滑融合的构造
2016-09-16刘华勇张大明谢新平王焕宝
刘华勇, 李 璐, 张大明, 谢新平,王焕宝
(安徽建筑大学 数理学院, 安徽 合肥 230601)
有理三角 Bézier曲线曲面光滑融合的构造
刘华勇, 李璐, 张大明, 谢新平,王焕宝
(安徽建筑大学 数理学院, 安徽 合肥 230601)
为了使自由曲线曲面在较为简单的条件下能够达到相对高阶的光滑拼接,并在不改变控制顶点的情况下自由调整曲线曲面的形状,构造了含多个形状参数的有理三角函数.基于该组基函数,定义了含多个形状参数的有理三角曲线曲面,并讨论了曲线曲面的光滑拼接条件.根据拼接条件,分别定义了由含多个形状参数的有理三角曲线曲面构成的分段组合曲线、分片组合曲面.这种新的曲线曲面能够自动保证组合曲线、曲面的连续性.数值实例的结果显示了该方法的有效性.
三角Bézier曲线;融合;连续性;封闭的曲线曲面
Journal of Zhejiang University(Science Edition), 2016,43(5):554-559,566
在计算机辅助几何设计(CAGD)中,Bernstein多项式和Bézier曲线曲面设计发挥了极其重要的作用.Bézier曲线曲面结构简单、计算相对方便、设计相对有效,但在实际应用中存在缺陷,即在控制多边形不变的情况下,无法调整曲线曲面的外形.有理的B-spline曲线曲面虽然在一定程度上克服了上述困难,但毕竟是有理形式,曲线曲面拼接的条件较复杂.
为了克服Bézier和B-样条曲线曲面的上述缺点,许多学者通过引入形状参数构建了新的曲线曲面.例如,李军成[1]介绍了一种构造任意类三次三角曲线的方法.严兰兰等[2]定义了形状及光滑度可调的自动连续组合曲线曲面. ZHANG[3-4]给出了带形状参数的三角多项式均匀B样条.这些曲线或曲面都与Bézier曲线或B-spline样条曲线曲面具有许多共同的基本特性,并可通过参数调整曲线曲面的形状.HAN[5]介绍了带参数的二次三角多项式样条曲线.刘华勇等[6]构造了带参数的二次三角样条曲线扩展.在自由曲线曲面造型中, 一般以多项式为基函数构造参数曲线曲面,而三角函数空间具有一些独特的性质,使得在三角函数空间中也能构造参数曲线曲面[7-14]. 但与曲线曲面的融合较为困难,且连续性不高[16-18].为了使自由曲线曲面在简单的条件下具有相对较高的光滑融合,同时在不改变控制顶点的情况下可以修改曲线曲面的形状,本文基于文献[2]的思想,构造了带形状参数的有理三角Bézier基函数,基于该组基函数,定义了λRC-Bézier曲线曲面,并详细讨论了该曲线曲面光滑拼接的条件.
1 带形状参数的有理三角Bézier基函数的定义及其性质
定义1对于t∈[0,π/2], ω1,ω2≥0,0≤λ1<1, 0<λ2≤1,记
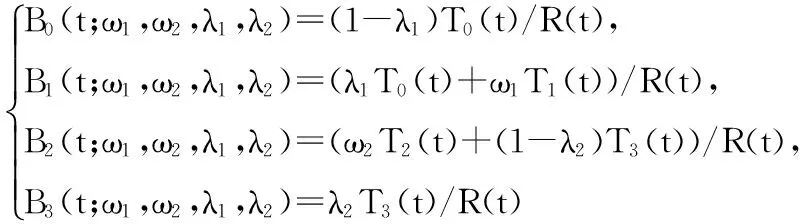
(2)
为带参数的有理三角Bézier基函数,简称为λRC-Bézier基函数.
性质1非负性:Bi(t;ω1,ω2,λ1,λ2)≥0,i=0,1,2,3;

性质3对称性:当ω1=ω2,λ1+λ2=1时,满足B3-i(t;ω1,ω2,λ1,λ2)=Bi(π/2-t;ω1,ω2,λ1,λ2),i=0,1;
性质4退化性:当ω1=ω2=1,λ1=0,λ2=1时,Bi(t;ω1,ω2,λ1,λ2)(i=0,1,2,3)退化为Ti(t)(i=0,1,2,3);
性质5端点性质:当t∈[0,π/2]时,为了书写简便,下式中的Bi(t;ω1,ω2,λ1,λ2)记为Bi(t).

进一步计算可知,
(1)当n为偶数,t=0时,有
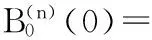
[2-n2ω1+(n2-2)ω2];
[2-n2ω1+(n2-2)ω2];
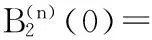
(n-2)(n-1)]/
[2-n2ω1+(n2-2)ω2];
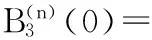
[2-n2ω1+(n2-2)ω2].
t=π/2时,有
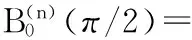
[2-n2ω2+(n2-2)ω1];
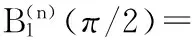
[2-n2ω2+(n2-2)ω1];
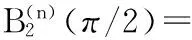
[2-n2ω2+(n2-2)ω1];
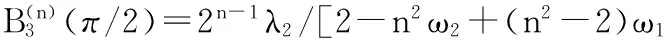
(2)当n为奇数,t=0时,
t=π/2时,有
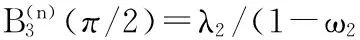
2 带形状参数的有理三角Bézier曲线的定义及其性质
定义2给定4个控制顶点Pi∈Rd(d=2,3;i=0,1,2,3),t∈[0,π/2],称
(2)为带参数的有理三角Bézier曲线,简称为λRC-Bézier曲线.
由λRC-Bézier基函数的性质,很容易得到λRC-Bézier曲线的性质:
性质6对称性:由基函数的对称性可知,如果保持λRC-Bézier曲线的控制顶点位置不变,只改变他们的先后次序,将得到的新曲线记作Q(t),则有Q(t)=R(π/2-t). 曲线的对称性表明,由相同控制多边形定义的λRC-Bézier曲线是唯一的.
性质7凸包性和保凸性:由λRC-Bézier基函数的非负性和权性知,曲线B(t)是控制顶点的加权平均,其权因子为λRC-Bézier基函数,因此λRC-Bézier曲线完全在特征多边形控制的凸包内.特征多边形为凸时,相应的λRC-Bézier曲线也为凸的,即曲线具备凸包性.
性质8几何不变性:曲线的外形由4个控制顶点的位置决定,与坐标系的选取无关.
性质9仿射不变性:对决定控制多边形的曲线进行仿射变换后,所得到的曲线就是原曲线经过相同仿射变换后的曲线.
性质10端点性质:
由基函数的端点性质知,
R(0)=(1-λ1)P0+λ1P1=P0+λ1(P1-P0);
R(π/2)=(1-λ2)P2+λ2P3=P2+λ2(P3-P2).
由上式知,曲线插值于控制多边形首边P0P1上的某点比例为(1-λ1)∶λ1,末边P2P3上的某点比例为(1-λ2)∶λ2.若λ1=0,则曲线插值于P0;若λ2=1,则曲线插值于P3.

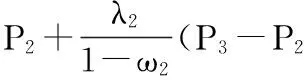
同样,经进一步计算,特别当n为奇数时,有
(3)
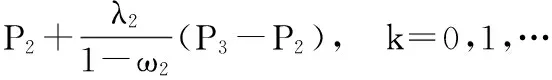
(4)曲线与控制多边形的首边相切且连续性更高,切点为多边形首边P0P1上的某点,比例为(1-λ1)∶λ1.若λ1=0,则切点为P0,同时曲线与控制多边形的末边相切,且连续性更高,切点为多边形首边P2P3上的某点,比例为(1-λ2)∶λ2;若λ2=1,则切点为P3.
性质11形状可调性:带有形状参数的λRC-Bézier曲线,随着参数ωi;λi(i=1,2)的改变,曲线会随之变化,其插值位置也随之不同,如图1所示.

图1 ω1,ω2,λ1,λ2取不同值时曲线的形状变化Fig.1 Influence of the value of ω1,ω2,λ1,λ2 on curve
3 带形状参数的λRC-Bézier曲线融合
3.1带形状参数的λRC-Bézier曲线的拼接
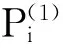
证明由性质知:
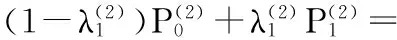

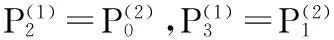


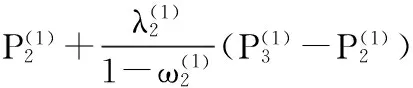
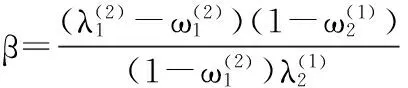
所以曲线满足G1连续.
由端点性质,并经进一步计算,当n为奇数时,可知:
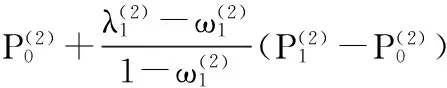
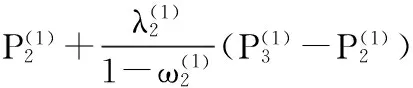
k=0,1,…,n;
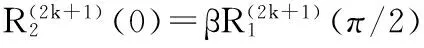
其中,
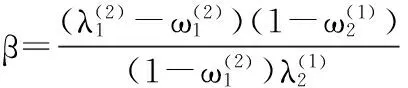
所以曲线满足G(2k+1)连续.
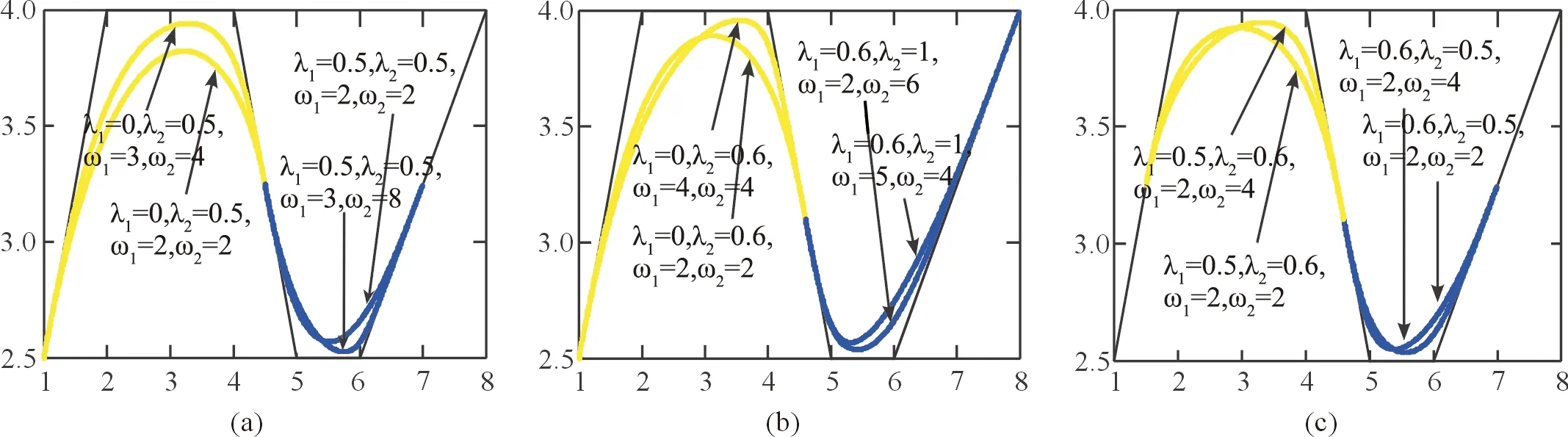
图2 带形状参数的λRC-Bézier曲线的拼接Fig.2 Joining λRC-Bézier curves with shape parameters
3.2带形状参数的λRC-Bézier曲线的组合
根据定理1所描述的性质,当给定任意的控制顶点时,可以定义包含多个形状参数的分段的组合曲线,并且使得曲线在连接点处能自动达到光滑拼接,见图2.


(5)
此组合λRC-Bézier曲线和三角样条曲线具有一些共同点:4个控制顶点决定一段曲线;当给定控制顶点时,曲线在连接点处能自动达到光滑拼接;并且每段曲线都含有多个形状参数,能决定该段曲线的形状,且具有强局部性.但他们之间也有不同:三角样条曲线在每段的拼接点处至多满足C2连续,而组合λRC-Bézier曲线在拼接点处可以达到G2k+1连续;在相邻2个曲线段之间,拼接的三角样条曲线只有1个不相同的控制顶点,而组合的相邻λRC-Bézier曲线段之间只有2个相同的控制顶点,因此需要的存储空间更少;修改三角样条曲线的其中1个控制顶点,至多可修改4条相邻曲线段的外形,而修改组合λRC-Bézier曲线的其中1个控制顶点,至多可修改2条相邻曲线段的外形,说明组合λRC-Bézier曲线比三角样条曲线具有更强的局部性;在不改变控制顶点的情况下,三角样条曲线无法对其进行形状修改,但组合λRC-Bézier曲线中存在形状控制参数,其形状可根据设计者的需求自由调整,见图3.

图3 带形状参数的λRC-Bézier曲线的组合Fig.3 Combination of λRC-Bézier curves with different shape parameters
3.3带形状参数的λRC-Bézier曲线设计

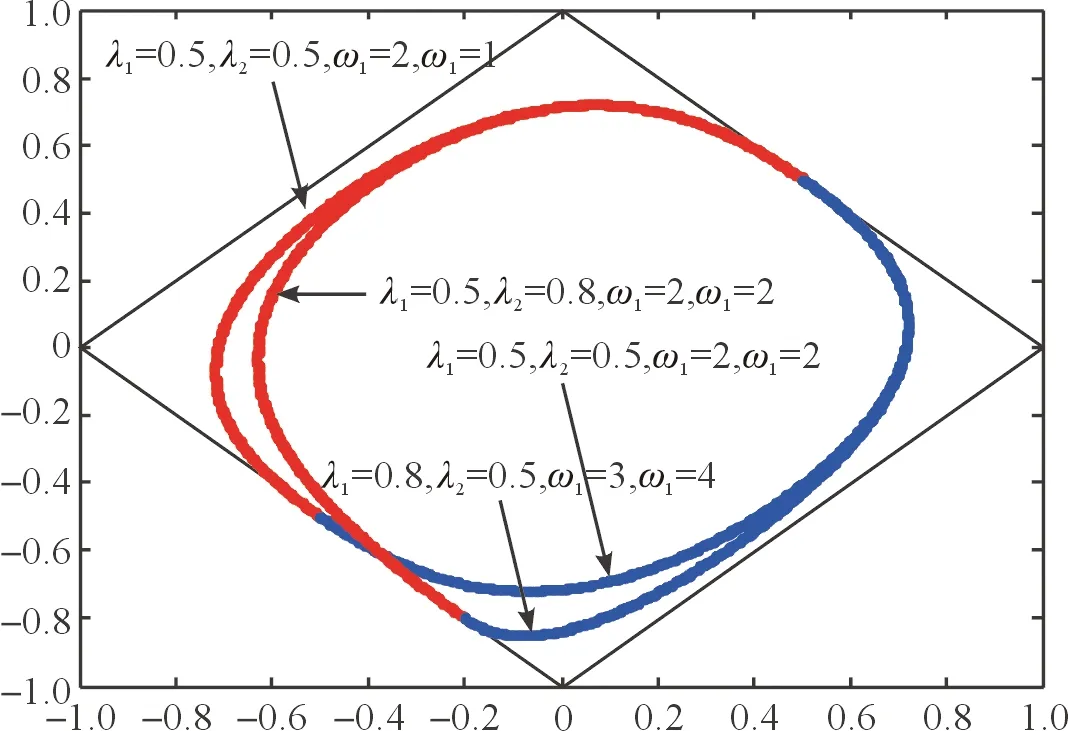
图4 闭合曲线构造的情形Fig.4 The case of closed curves
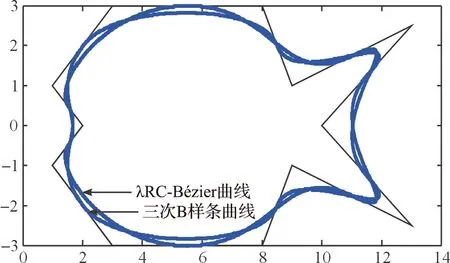
图5 λRC-Bézier曲线和三次B样条曲线的比较Fig.5 Comparison of λRC-Bézier curve with B- spline curve
4 带形状参数的λRC-Bézier曲面的定义及其性质
定义4给定一组16个控制顶点Pij∈R3(i,j=0,1,2,3),u,v∈[0,π/2],称
Bj(v;ω1v,ω2vλ1v,λ2v)Pij
(6)
为带形状参数的λRC-Bézier曲面.

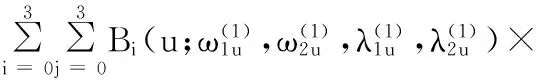
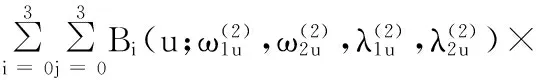
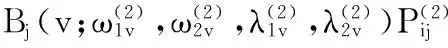

图6 λ,ω取不同值时曲面的光滑融合Fig.6 Smooth blending of surfaces with different value of λ,ω
5 结 论
给出的λRC-Bézier曲线具有形状可调性,在构造带形状参数函数时,曲线的拼接条件相对较简单,且连续性相对较高.所以在相同拼接条件下,只需要简单地修改形状参数值就可以修改曲线的插值位置、连续性等.文中还给出了带形状参数的曲面的定义和一些实例,由这些定义知,λRC-Bézier曲线可以更好地控制曲面,且连续性较三角样条方法高,虽然不需要考虑拼接等问题,但这些常用三角样条的曲线曲面至多只能满足C2连续,如果需要更高阶连续,则必须由更高次三角样条曲线曲面来解决,从而减弱了三角样条曲线曲面的局部性.本文构造的组合拼接曲线曲面具有三角样条不具备的一些优点.
[1]李军成.一种构造任意类三次三角曲线的方法[J].小型微型计算机系统,2011,32(7):1442-1445.
LI Juncheng. A method for constructing arbitrary quasi-cubic trigonometric curves[J]. Journal of Chinese Computer Systems, 2011,32(7):1442-1445.
[2]严兰兰,韩旭里.形状及光滑度可调的自动连续组合曲线曲面[J].计算机辅助设计与图形学学报,2014,26(10):1654-1662.
YAN Lanlan, HAN Xuli. Automatic continuous composite curve and surface with adjustable shape and smoothness [J]. Journal of Computer-Aided Design&Computer Graphics,2014,26(10):1654-1662.
[3]ZHANG Jiwen. C-curves: An extension of cubic curves[J]. Computer Aided Geometric Design,1996,13(3):199-217.
[4]ZHANG Jiwen. C-curves: Two different forms of C-B-Splines[J]. Computer Aided Geometric Design,1997,14(l):31-41.
[5]HAN X. Quadratic trigonometric polynomial curves with a shape parameter[J]. Computer Aided Geometric Design, 2002,19(7):503-512.
[6]刘华勇,李璐,张大明. 任意阶参数连续的三角多项式样条曲线曲面调配[J].浙江大学学报:理学版,2014,41(4):413-418.
LIU Huayong, LI Lu, ZHANG Daming. Blending of the trigonometric polynomial spline curve and surface with arbitrary continuous order[J]. Journal of Zhejiang University:Science Edition,2014,41(4):413-418.
[7]徐迎博,喻德生.带形状参数的二次三角多项式Bézier曲线形状分析[J].浙江大学学报:理学报,2013,40(1):35-41.
XU Yingbo, YU Desheng. Shape analysis of quadratic trigonometric polynomial Bézier curves with a shape parameter[J]. Journal of Zhejiang University:Science Edition,2013,40(1):35-41.
[8]王文涛,汪国昭.带形状参数的三角多项式均匀B样条[J].计算机学报,2005,28(7):1192-1198.
WANG Wentao, WANG Guozhao. Trigonometric polynomial uniform B-spline with shape parameter [J]. Chinese Journal of Computers,2005,28(7):1192-1198
[9]李军成,赵东标,杨炼.拟三次三角样条插值曲线与曲面[J].小型微型计算机系统,2013,34(3):680-684.
LI Juncheng, ZHAO Dongbiao, YANG Lian. Quasi-cubic trigonometric spline interpolation curves and surfaces[J]. Journal of Chinese Computer Systems,2013,34(3):680-684
[10]吴晓勤.带形状参数的Bézier曲线[J].中国图象图形学报,2006,10(2):269-275.
WU Xiaoqin. Bézier curve with shape parameter [J]Journal of Image and Graphics,2006,10(2):269-275.
[11]ZHANG J W, KRAUS F L. Extending cubic uniform B-splines by unified trigonometric and hyperbolic basis[J]. Graphical Models,2005,67(2):100-119.
[12]彭丰富,田良.带形状控制的自由曲线曲面参数样条[J].中国图象图形学报,2015,20(11):1511-1516.
PENG Fengfu, TIAN Liang. Parameter spline for free-form curve and surface [J]. Journal of Image and Graphics, 2015, 20(11):1511-1516.
[13]严兰兰,韩旭里.具有多种优点的三角多项式曲线曲面[J].计算机辅助设计与图形学学报,2015,27(10):1971-1979.
YAN Lanlan, HAN Xuli. Trigonometric polynomial curve and surface with many advantages [J]. Journal of Computer-Aided Design & Computer Graphics,2015,27(10):1971-1979.
[14]CHEN Q Y, WANG G Z. A class of Bezier-like Curve[J]. Computer Aided Geometric Design, 2003,20(1):29-39.
[15]HU Gang, QIN Xinqiang. The construction of λμ-B-spline curves and its application to rotational surfaces
[J]. Applied Mathematics and Computation,2015,266(2):194-211.
[16]LIP M, MATTHEW M F Y. Blending of mesh objects to parametric surface [J]. Computers & Graphics,2015,46(2):283-293.
[17]ZHU Y P, HAN X L. New cubic rational basis with tension shape parameters[J].App Math J Chinese Univ,2015,30(3):273-298.
Smooth blending of rational trigonometric Bézier curves and surfaces.
LIU Huayong, LI Lu, ZHANG Daming, XIE Xinping, WANG Huanbao
(SchoolofMathematic&Physics,AnhuiJianzhuUniversity,Hefei230601,China)
In order to achieve high level of smooth blending between the free form curves and surfaces in relatively simple conditions and easy shape adjustment of the curves and surfaces without changing their control vertices, a set of rational trigonometric Bézier basis functions with multiple shape parameters are constructed. Based on these basis functions, the rational trigonometric Bézier curves and surfaces with multiple shape parameters are defined, and the conditions for smooth joining of these curves and surfaces are derived. Following the above conditions of blending, the piecewise composite rational curves and surfaces with multiple shape parameters are defined, which automatically meet with the higher order continuity. The results of numerical examples show the effectiveness of the method.
trigonometric Bézier curve; blending; continuity; closed curves and surfaces

2015-08-10.
国家自然科学基金资助项目(61402010, 61471003); 安徽省高等学校自然科学研究项目(KJ2015A328; KJ2015JD16; KJ2016A151 ).
刘华勇(1972-),ORCID:http://orcid:org/0000-0002-9330-1149,男,硕士,副教授,主要从事计算机辅助几何设计研究,E-mail:aiaiwj@126.com.
10.3785/j.issn.1008-9497.2016.05.011
TP 391
A
1008-9497(2016)05-554-06
