整合资产收益策略与年金化最优退休决策:异质性风险偏好与规避视角
2016-09-15王云多
王云多
(黑龙江大学经济与工商管理学院黑龙江哈尔滨150080)
整合资产收益策略与年金化最优退休决策:异质性风险偏好与规避视角
王云多
(黑龙江大学经济与工商管理学院黑龙江哈尔滨150080)
随着我国老龄化加剧,退休支付策略中阶段提取计划备受老年人青睐。为深入研究阶段提取计划的价值,本文在含有资本市场随机性和寿命不确定性的效用函数中研究不同退休支付计划,基于不同风险规避程度评价这些退休支付计划,在此基础上,整合资产收益和年金化退休决策。研究显示,与选择退休时全部年金化作比较,整合策略能提高中低风险规避退休者25%~50%的福利。如果考虑个人在退休后最优时点转向购买固定年金引起的福利改变,这提供给退休者年轻时从股票溢价受益的机会,也可使退休者开发死亡率信用。研究表明,对于适中的风险规避者而言,最优转换年龄介于75—80岁之间。
资产分配;年金化;退休决策
一、问题的提出
随着人口老龄化加剧,为防止老年贫困,如何理财备受人们关注,退休者需要考虑如何将他们积累的资产转换为不会很快耗尽的稳定退休收入流。基于此,有人选择购买生存年金,也有人将资产收益计划(阶段提取计划)作为一个更好的选择。但是,无论选择生存年金抑或资产收益计划,由于没有充分考虑到寿命不确定和异质性风险偏好对个人退休决策的影响,都不能真正保证个人退休后获得稳定收入流,本文在比较不同退休支付策略的基础上,提出整合最优资产收益与年金化决策,旨在指导人们如何通过同时使用与投资有关的退休计划和生存年金,以优化他们的退休投资组合。
为了探讨这一最优决策问题,本文通过在一个效用函数考虑死亡率、利率和资本市场风险等因素,研究不同阶段提取计划和内生转换策略,从而拓展了这方面的研究。首先,将阶段提取计划(包括分散投资组合)和一次性提取年金作比较。这允许本文决定对于特定风险规避以及消费者而言,哪一提取规则更适合。其次,研究表明,最优退休决策不需要在年金化个人所有财富和选择阶段提取计划之间做出选择,能容纳混合型(即期和延期)投资组合,这一投资组合既包括年金也包括共同投资基金。
二、相关文献评述
近年来,国内外学者分别从年金化退休决策,影响年金化退休决策的因素,以及资产收益与年金化退休决策关系角度做了深入研究。就年金化退休决策而言,多数研究认为由于年金合同提供了稳定收入,能防止退休者较早耗尽全部资产风险,在满足一定条件的情况下,个人退休后将所有财富年金化。如Yuari(1965)研究指出,只要保证年金精算公平,且退休者没有遗赠动机,个人退休后将用全部财富购买年金[1]。Blake等(2003),Kingston和Thorp(2005),Davidoff等(2005),Milevsky和Young(2006)拓展了Yuari的研究,研究指出只有在完全竞争市场环境下,个人资产才会全部年金化[2-5]。Albrecht和Maurer(2002)还研究了退休者何时购买年金的年金化决策[6],
然而,多数国家可得证据显示,很少有退休者用他们可处置的财富购买年金,这就是所谓的年金之谜。年金之谜表明一些因素影响了年金化,部分人认为年金之谜是由于购买年金会使资产失去流动性,也有人认为遗赠动机也减少了退休者年金化财富需求。其他有关人们不愿意购买年金的解释还包括保险公司的高额附加保费,家庭内部存在的长寿风险共担能力,年金购买者和销售者之间信息不对称,以及其他年金化资产的存在(Dushi和Webb,2004)[7]。另外,在低利率环境下,相比共同基金投资,年金视乎相对昂贵。还有人认为年金之谜可能是人们相信他们通过继续投资他们的退休资产在未来会获得更多收益。可是,就投资组合而言,退休者必须在投资多少用于股票和债券市场之间做出选择,一些学者根据经验建议将投资组合分成60%为股票,40%为债券(Gerrard等,2004;Cocco等,2005)[8-9]。与购买生存年金相比,如此一个资产收益计划有几个优点:它提供了更大流动性,更高资本市场收益,更多消费和更多遗赠机会。然而没有提供长寿风险共担,这一资产收益计划也表明退休者存在投资风险,退休者可能在死前耗尽资产。这将产生福利波动,可能导致福利显著下降,低于生存年金收益。
就资产收益与年金化退休决策关系而言,先前的研究将年金化和资产收益计划非常牵强地联系在一起。例如,一些研究仅允许退休者购买不变资产组合(Browne等,2003)[10],或仅允许购买有限年金选择组合(Milevsky和Young,2007)[11]。一些研究只允许退休者做出一次性年金化决定,不允许他逐级年金化(翟永会,王晓芳,2009;郭磊,2009)[12-13]。最后,部分研究为比较收益策略,使用短缺风险方法研究资产收益决策(Charupa和Milevsky,2002)[14],Dus等(2005)通过量化风险研究固定、可变资产收益,将风险收益与固定年金收益作比较[15]。而一些研究将有或没有遗赠动机强加给个人资产收益决策(王云多,2014)[16]。
已有的研究并未考虑利率不同对资产收益以及年金化退休决策的影响,本文在已有研究的基础上,通过将利率引入资产收益与年金购买决策,并将二者加以整合,拓展了年金化退休决策研究,探讨是否退休者可能受益于如下一个混合策略,在这一混合策略下,投资组合既包括生存年金,也包括阶段提取计划。如此一个混合策略由于减少了收入下降到低于生存年金的风险而直观上似乎更有吸引力。
三、不同退休收益计划的比较研究
假设退休者被赋予一个初始财富水平W0,这一财富能或者被用于以成本C0购买一个支付不变名义年金收益的单一保费生存年金,或者用于购买一个直到基金被耗尽的阶段提取计划(Dus等,2005)。
(一)不变生存年金计划
当消费者购买生存年金时,只要活着每年将被支付一个不变数量年金。采用精算等价原则,本文通过计算支付给投保人预期收益的现值来决定年金的保费,年龄为n岁的退休者年金因子τn为
(1)
式(1)中z代表假定的退休者死亡年龄;tpn=pn……pn+t-1是年龄为n岁退休者活到n+t岁的累积概率。其中pn+1代表年龄为n岁的人年复一年的存活概率,δ代表消费因子,rt代表t期利息率。基于这些假定,计算恒派息年金。这一不变收益生存年金构成具有独一无二收益资产链,生存年金以年金受益者生存为支付条件。年金购买者死亡后资产在存活者中间分配,相应的一个活着的人一期年金总收入是他资产收益加上死亡信誉的函数。其他情况相同,个人越老,死亡信誉越高。
(二)阶段提取计划
如果退休者转向寻求一个阶段提取计划,退休者既可以选择一个固定收益提取计划,也可以选择一个可变收益提取计划。如果退休者选择固定收益提取计划,直至死亡,退休者将付给自己一个不变收益Rt。只要基金允许,固定收益计划将复制一个生存年金收益。与此同时,退休者应保留流动性资产和一些遗产以防过早死亡。
如果退休者选择可变收益提取计划,可有如下三个方案:即固定百分比计划,1/M计划(即最大可能持续支付计划,M代表退休者余命)和1/E(M)(E(M)代表预期退休者余命)计划。首先,就固定百分比计划而言,每期从剩余财富提取的比例不变,不同时期收益(Rt)与财富(Wt)比率固定(见式(2))
(2)
式(2)中εt代表t期年金收益与财富比,这一阶段提取计划的主要优势在于不需要考虑支出阶段最大可能持续时间和退休者私人信息。另外,根据最大可能持续支付计划,1/M计划决定提取比例,假定代表性个人n岁退休,最大存活年龄设定为j岁,那么在他退休期开始时每年最大收益数量M=j-n+1,因此,对于60岁退休的人而言,假定最大寿命为90岁,则退休开始时最大收益数量为31。退休者第一年收益是1/M初始资产,退休者第二年收益是价值1/(M-1)的剩余资产,直到退休者死亡或达到最大年龄。因此在1/M计划下提取份额可变,随年龄增长而上升。在t年开始收益与财富比(t=0,1,…M-1)如下
(3)

图1 不同阶段提取计划下收益与财富之比
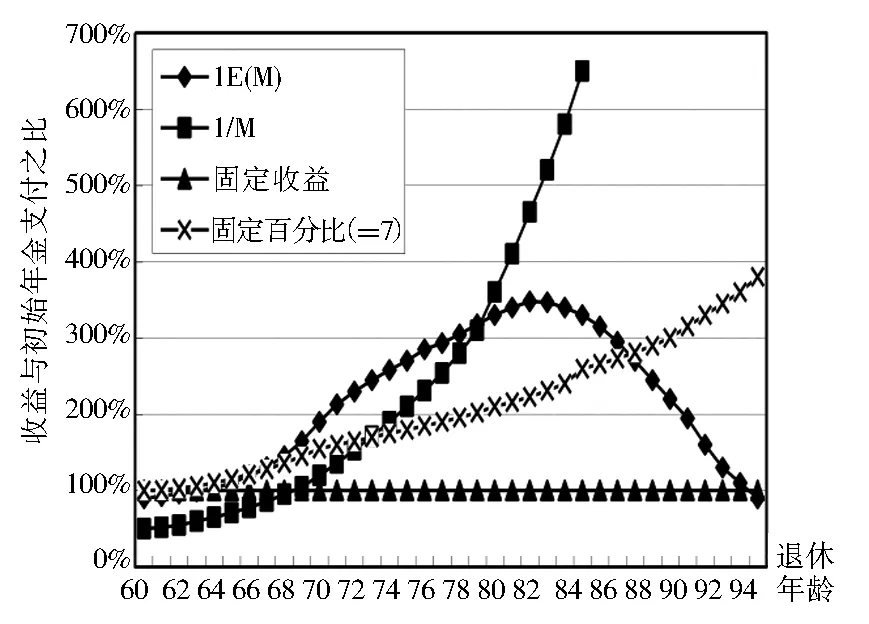
图2 以存活为条件的不同阶段提取计划下预期收益比率
注释:本图将四个阶段提取计划(以存活为条件)下的预期收益与生存年金作比较,股票和债券的基本资产配置比例为60%~40%。
最后,1/E(M)计划考虑了退休者预期余命。那么,对于一个年龄为n岁的退休者而言,活着情况下t期收益与财富之比如下
(4)
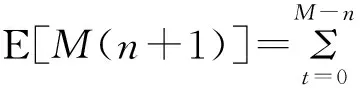
图1列出这三种阶段提取计划下退休者提取率。固定百分比计划下提取率为水平线(不随年龄变化而变化),而1/M和1/E(M)计划下提取率随年龄变化呈上升趋势。1/M计划开始时提取份额较小,在迅速增加到收益与财富比为1的年龄(即在效用分析中假设的最大年龄)之前仍保持适中。相比之下,1/E(M)提取计划以一个适度提取百分比开始,凸性小于1/M计划;结果,相比1/M计划,1/E(M)提取计划包含一个更早投资组合支取。
(三)预期收益和不同阶段提取计划风险评估
购买一个阶段提取计划的退休者必须在股票和债券之间配置他剩下的资产。为了模拟不同阶段提取计划投资选择的收益情况,本文假设两种资产的市场价格随机动态变化。在下面分析收益风险状况时,由于财务顾问在分析退休资产组合时通常推荐股票和债券之间60%~40%的比例关系,本文假设退休资产重新平衡不断保持股票和债券之间的这一比例关系不变。
以生存为条件,图2将不同阶段提取计划下期望收益路径与生存年金作比较。首先,就固定收益计划而言,在个人退休后平均收益等于生存年金收益。固定百分比计划也在第一年开始于收益等于生存年金收益,随着退休年龄上升,养老金账户的期望总收益率超过不变的收益与财富比,平均收益也上升。
相比于固定收益计划,1/M计划和/E(M)计划支付模式稍有不同。1/M计划在69岁之前一直提供较低预期收益,但预期收益在那之后迅速增加,直至非常高水平。1/M计划在个人退休早期收益较低,事实上低于投资组合的年预期收益。相应地,退休者继续增加早期储蓄,这能提高后期预期收益。1/E(M)计划以一个较低的年收益开始,然后当退休者仍相当年轻时(64岁)上升超过固定年金收益。此后,1/E(M)收益达顶峰(83岁)并开始下降,由于很少有财富仍留在账户中,尽管提取份额上升,在某点预期收益一定下降。
提及一个测量阶段提取计划的最坏情况仍有建设性指导价值,图3描绘了相比生存年金的最小可能收益(PMR)。本文将最小可能收益度量标准定义如下(置信水平α=1%)
P(Rt (5) 图3 以存活为条件不同分配计划下可能的最小收益 注释:本图阐明了最小可能收益(1%置信水平下)或四个阶段提取计划的风险。 以存活为条件,最小可能收益分配方案代表每期第一个百分位的收益分布。换句话说,如果退休者仍活过t年,他将有99%概率从等于或高于最小可能收益方案得到回报。这一度量看到了收益分布的下尾分布,因此它能被解释为一种最坏情况风险测度。 研究最小可能收益分配方案很重要,起初,对于固定收益计划而言,最小可能收益与年金收益相同,但随着时间流逝而迅速下降,在75岁时变为零,即退休者花光了钱。相比之下,就所有可变提取计划而言,最坏情况下的收益低于退休后初始15年的支付。退休早期阶段,1/M和1/E(M)计划下最小可能收益都低于年金收益,此后不断增加。在80岁时,1/M计划的最小可能收益甚至超过年金收益。相反,1/E(M)计划下最小可能收益从未超过年金收益。固定百分比计划下的最小可能收益仍处在很低水平,从未恢复。总体上,所有分配方案检验了包括最坏可能风险发生情况,这一风险对于退休者而言相当高。 上面描述的预期收益和最小可能收益可用于探析不同收益策略下风险和收益测度。下面,本文转向一个以效用分析为基础的研究方法,这一方法考虑含有风险规避和时间偏好等因素。 (一)风险规避对收益分配计划选择的影响 为理解不同收益分配模式将如何由不同风险规避的人评价。本文采用具有不变相对风险规避程度的离散时间效用函数。代表来自阶段提取计划的名义年金收益,而At代表来自t期生存年金收益。Wt代表退休账户中剩余资产,也代表退休者意外死亡情况下的遗产。本文假设基于收到的总收益和死亡时留下的遗产定义退休者效用函数U0,设定效用函数形式如下 (6) 参数γ反映了个人相对风险规避程度,也反映了个人加入跨期替代消费的意愿。当收益不确定时,因为资产收益的随机性,这一参数在评估不同分配计划时起着重要作用。下面,本文列出使用不同风险规避系数的结果。分类如下:设定最小风险规避者风险规避系数低于1,适度风险规避者风险规避系数介于1和5之间,高风险规避者风险规避系数大于5。 贯彻这一方法首先需要选择每一提取计划下最优静态股票和债券资产分配(πt),就每一风险规避水平而言,保持其他参数固定,这一问题的随机构成源自死亡日期和资产收益的不确定。下面,本文基于每一阶段提取计划的资产分配计算预期的一生效用(除了固定收益计划),然后将这一效用水平转化为一生等价名义年金收入流,将其直接同名义生存年金作比较。最后,作为常规支付模式和年金,本文也计算在每一风险规避下没有机会进入年金市场的人的最优(可变)提取计划。使用随机动态计划求解。这意味着既能选择εt的最优提取模式,也能选择与它相关资产分配路径πt,以最大化式(6)中的预期一生效用函数。年金当量收入流可以被解释为名义生存年金流,如果它遵循提取计划,这一名义生存年金流将提供给退休者同样水平的一生效用。 图4 不同风险规避程度下各种分配计划的年金当量流 注释:本图介绍了名义生存年金收入当量流,只要遵循一个特别的分配计划,提供给退休者等价的一生效用。 图4列出不同风险规避程度下各种分配计划的年金当量流,由图4可知,风险规避在影响收益偏好方面起着重要作用。此外,因为固定收益计划使退休者存在用尽资产的风险,固定收益计划仅和低水平风险规避程度(γ<1)一致。在不同风险规避水平下固定收益计划被所有其他收益计划和年金路径支配,令人吃惊的是在不同风险规避程度下固定百分比计划几乎均受偏好。在所有风险规避水平下固定百分比计划支配1/M计划,它比中、低水平风险规避的年金更有吸引力。在这一意义上本文的研究支持固定收益计划。 本文也发现在所有可变收益计划中1/M计划最不受欢迎。相比之下,1/E(M)计划对于中低等风险规避退休者更具有吸引力,但它在高风险规避者那里不受欢迎。就极高风险规避程度而言,1/E(M)计划是所有可变收益计划中最不受欢迎的。相比其他收益计划和年金,最优提取计划给中低风险规避的退休者提供更高效用。基于给定的这些参数,仅有高风险规避者将发现固定年金有吸引力。为了阐明相关程度,对于一个适度风险规避(γ=3)的60岁退休者,与购买年金相比,选择固定百分比计划将使收益提高16.8%,选择1/M计划将使收益下降34.7%;选择1/E(M)计划将使收益提高9.7%,选择最优提取计划将使收益提高30.4%。对于极端风险规避退休者(γ=9)而言,与购买年金相比,选择固定百分比计划将使收益下降17.6%,选择1/M计划将使收益下降52.4%,选择1/E(M)计划将使收益下降63.4%;选择最优提取计划将使收益下降3.1%。 图5描绘了不同风险规避程度下固定和可变收益计划的最优资产分配。首先,研究揭示固定收益计划的资产分配(仅与极端风险偏好有关)中股票份额占47%。其次,对于所有可变阶段提取计划而言,资产分配模式相同,但收益随风险规避程度变化而变化。风险规避值为2时,退休者股票持有率为100%。随着风险规避程度上升,股票持有比例下降。对于风险规避为4的人而言,一般研究建议股票和债券持有比例为6/4,但是曲线斜率变缓,以至于高风险规避者最优持有股票仍为40%。 图5 固定和可变收益分配计划的最优股权融资风险 注释:本图说明与每一支付计划有关的最优资产分配。 图6 最优的股票、债券和年金组合 注释:本图描述了不同风险规避程度下1/E(M)计划下的股票和年金的最优组合。 (二)年金提取计划的混合组合 为了研究是否一个混合组合可能比单独策略能提供更多效用。本文评估一个生存年金产品与一个阶段提取计划相结合的情况,而1/E(M)是主要收益原则。本文首先考虑60岁退休者选择多少用于年金化和多少保留在提取账户中。下面,本文考虑退休者默认进入1/E(M)计划,然后他被允许将剩余财富转化为年金。当设定退休时混合计划,本文选择最优投资组合权重与最优年金份额一致。退休者决定60岁初始年金化份额,剩余部分投资于1/E(M)提取计划 (7) 图6比较了那些必须在退休时设定的混合计划情况。由图6可知,那些低风险规避者选择非年金化,但随着风险规避程度(γ)上升到1.5,年金需求迅速上升。风险规避程度为4的退休者投资62.5%的财富用于年金化,37.5%的财富留在1/E(M)提取计划和持有股票。在这一意义上,随着风险规避程度上升,年金挤出债券和1/E(M)提取计划。 表1归纳当60岁退休者被允许在未来某一时期将其资产全部年金化时留在1/E(M)提取计划下的结果,然后将这一策略与初始混合策略作比较。本文从前面的提取计划分析中设定投资权重和提取份额,试图决定个人何时完全转向年金化。最优问题是去发现最优转换年龄:本文构建了年金和1/E(M)提取计划的跨期投资组合,将计算所得收益与60岁退休时完全年金化收益作比较。研究表明,如果个人风险规避程度(γ)超过4.5,则这个退休者应立即年金化,具有适度风险规避程度(γ=3)的退休者延期年金化他的财富直到75岁。与60岁强制年金化相比,个人延期15年年金化多收益11%。随着风险规避程度下降,收益和年金化年龄上升。 表1 混合策略的等价年金流百分比变化 注:第一排旨在说明就不同风险规避水平而言,最佳年金化年龄(转换年龄),即1/E(M)阶段提取计划下的最优转换年龄,第二排比较了直接混合策略下等价年金流和60岁时完全年金化收益。 本文考虑的资本市场类型和1/E(M)提取计划更为现实,估计的不同风险规避程度下收益数量与已有研究一致(Brown,2000;Chen和Milevsky,2003)[17-18]。尽管构建风险偏好退休者的投资组合,但风险规避适中的退休者将受益于混合提取策略和初始生存年金,即使风险规避为10的退休者仍在一个阶段提取计划中持有很少资产。 先前的分析已经假设退休者决定他的最初最优转换年龄,未考虑未来情况,下面,本文使用动态方法让退休者对产出曲线变化作出反应。当退休者决定转换时间,效用最大化问题可被写为 (8) 图7 不同风险规避程度下1/E(M)提取计划的最优年金化年龄 图7描绘了两个不同退休者最优年金化年龄。毫无疑问,利率越高,退休者年金化,他的全部资产越快。可是,一个风险偏好退休者比风险规避退休者也需要一个更高的短期利率。因为死亡信誉随时间流逝而增加,替代先前由短期利率产生的成本优势,转换边界拟凹。图7描绘了利率水平和死亡信誉的混合效应。由图7可知,风险规避越低,短期利率越高,越能引起退休者年金化他的资产。 (三)深入研究及其结果分析 随后,描述利率政策的其他结果。首先,不考虑包括在保费中的管理成本,仅适当改变了结果。其次,假定存在正向遗赠动机,所有提取计划似乎更有吸引力。更进一步讲,风险规避水平越低,采用一个特别提取计划的收益越大。例如,在有遗赠动机情况下,相比年金当量流,固定收益方法变得更有吸引力。对于风险规避程度大于等于1的情况,在退休期开始,完全年金化和转换策略不可行,可是,遗赠动机水平对特殊退休计划选择顺序不敏感。 本文已经检验了结果对其他因素的敏感度。首先,考虑了死亡信誉的信息不对称。假定可调整1/E(M)计划用于年龄的更高生存概率,像保险公司假定的那样健康的退休者,在设定年金升水时,将更早年金化他的财富。相反,一个健康状况低于平均水平的退休者倾向于延期年金化,这取决于他的风险规避程度。可是,如果由于计划原因,1/E(M)不能被调整以适用于更高生存概率,退休者将偏好更晚年金化。相应地,这一例子表明那些关于死亡信誉非对称信息能解释为什么那些相信自己健康低于平均水平的人更可能延期年金化。下面,本文考虑通货膨胀对决策过程的影响。为了深入研究这一点,本文按每年3%利率贴现每一收益和年金收入流,将产生的效用水平转入一个名义生存收入流。然后,基于名义生存收入流,计算名义和实际策略间的差别。表2列出所有初始保费为1元的百分比值,所有风险规避程度和退休策略的差异相对较小。 表2 不同风险规避程度下实际和名义策略之间等价年金收入流的差别 注:就实际策略而言,本文按照年利率3%贴现每一收益和年金收入,将效用水平转换为一个名义终生收入流。然后基于名义终生收入流计算名义和实际策略之间的实际差别。 老龄化趋势使大量就业人口日益接近退休年龄,如何防止老年贫困是这些人最为关心的问题。老年人关注如何最有效转换积累的资产使其成为退休收入流,以防止太快耗尽他们的财富。本文的分析框架有利于比较单独购买生存年金的价值,与阶段提取计划(背负分散投资组合),也有这两种策略的混合。研究揭示,恰当的混合取决于退休者对待风险的态度,也取决于基本的经济和人口统计假定。特别是,当评估提取计划时,例如评估1/E(M)计划、固定百分比计划、1/M计划和固定收益计划,研究发现以下几点。 (1)对于风险偏好者,固定百分比计划较有吸引力。相应地,这一计划被证实备受那些在金融咨询行业工作的人偏好。 (2)1/E(M)计划受中低风险规避者青睐,不受高风险规避者青睐。固定收益计划不受多数退休者喜爱,因为它有潜在用尽资产的风险。对于投资者而言,1/M计划比其他任何可变提取计划做得更差。 (3)通过比较单一提取计划与整体投资组合的即时年金,研究揭示,当退休者风险规避程度较高和遗赠动机较低时,年金作为单一产品更有吸引力。提取计划支配中低风险偏好的年金,因为退休者可通过投资于资本市场获得收益。 (4)通过研究混合策略,这一策略中退休者既投资一些资产,也购买年金。在这种情况下年金决策发生在法定退休年龄,研究发现,对那些风险规避中性的人而言,年金更有吸引力,当退休者既能持有年金,也能持有阶段提取计划作为一个混合策略时。阶段提取计划对高风险规避者有吸引力,从资产配置角度看,当风险规避程度提高时,年金首先挤出债券。随着风险规避程度进一步上升,在资产组合中,年金代替了股票。当退休者可转向年金时,个人最佳年金化年龄对风险规避程度和利率敏感。较少风险规避者将等待更长时间直到他们转向一个年金。相比之下,高风险退休者愿意在低利率环境下年金化,但较高利率要求在风险偏好者中引导年金化。 本文研究结果与在退休市场上一定范围内金融服务供应商和监管者有关。短期资本经营者和保险公司应记住许多退休者持有次优资本配置,正如本文所示,随着风险规避上升,年金首先挤出债券,在更高水平风险规避,在退休者组合资产中年金取代股票,如果年金化太早,会导致风险规避程度低的投资者存在巨大的效用损失,如果不考虑遗赠动机,基于给定模型参数化,存在一个敏感年金化年龄。本研究表明,由于假定投资者有机会通过阶段提取计划进入股票市场,退休者发现与股票有关的阶段提取计划有一定吸引力,这一假定符合现实。 [1]Yaari M E.Uncertain Lifetime, Life Insurance, and the Theory of Theconsumer[J]. Review of Economic Studies, 1965,32(2):137-150. [2]Blake D,Cairns A J G, Dowd K. Pension Metrics II: Stochastic Pension Plan Design During the Distribution Phase[J].Mathematics and Economics,2003,33(1):29-47. [3]Kingston G, Thorp S. Annuitization and Asset Allocation with HARA Utility[J]. Journal of Pension Economics and Finance, 2005, 4(3): 225-248. [4]Davidoff T, Brown J R, Diamond P A. Annuities and Individual Welfare[J]. American Economic Review, 2005,95(5):1573-1590. [5]Milevsky M A, Moore K S,Young V. Asset Allocation and Annuity-Purchases Strategies to Minimize the Probability of Financial Ruin[J]. Mathematical Finance,2006,16(4):647-671. [6]Albrecht P,Maurer R. Self-annuitization, Consumption Shortfall in Retirement and Asset Allocation: The Annuity Benchmark[J]. Journal of Pension Economics and Finance, 2002,1(3): 269-288. [7]Dushi I,Webb A. Household Annuitization Decisions: Simulations and Empirical Analyses[J]. Journal of Pension Economics and Finance, 2004,3(2):109-143. [8]Gerrard R, Haberman S, Vigna E. Optimal Investment Choices Post-Retirement in A Defined Contribution Pension Scheme[J]. Mathematics and Economics, 2004,35(2): 321-342. [9]Cocco J F, Gomes F J, Maenhout P J. Consumption and Portfolio Choice over the Life-Cycle[J]. Review of Financial Studies,2005,18(2):491-533. [10]Browne S, Milevsky M A, Salisbury T S.Asset Allocation and the Liquidity Premium for Illiquid Annuities[J]. Journal of Risk and Insurance,2003,70 (3):509-526. [11]Milevsky M A, Young V R. The Timing of Annuitization: Investment Dominance and Mortality Risk[J]. Mathematics and Economics, 2007,40(1):135-144. [12]翟永会,王晓芳.退休后企业年金的最优投资策略及领取方案研究[J].产业经济研究,2009(6):52-59. [13]郭磊.寿命不确定与企业年金退休后投资决策[J].同济大学学报(自然科学版),2009(12):1712-1714. [14]Charupat N, Milevsky M A. Optimal Asset Allocation in Life Annuities[J]. Mathematics and Economics, 2002,30(2):199-209. [15]Dus I, Maurer R, Mitchell O S. Betting on Death and Capital Markets in Retirement: A Shortfall Risk Analysis of Life Annuities versus Phased Withdrawal Plans[J]. Financial Services Review, 2005,14(4):169-196. [16]王云多.整合工作、退休与一生收益决策的最优投资组合研究[J].中国管理科学,2014(6):27-33. [17]Brown J R, Poterba J M. Joint Life Annuities and Annuity Demand by Married Couples[J]. Journal of Risk and Insurance, 2000,67(4):527-553. [18]Chen P, Milevsky M A. Merging Asset Allocation and Longevity Insurance: An Optimal Perspective on Payout Annuities[J]. Journal of Financial Planning, 2003,16(6):52-62. 责任编辑王丽英 Integrate Asset Allocation and Optimal Annuitization of Retirement:Perspective of Heterogeneity Risk Aversion WANG Yun-duo (School of Economics and Business Administration, Heilongjiang University, Harbin 150080, China) This paper studied different retirement payment schemes in utility function, which included randomness of capital market and life uncertainty, and evaluated these schemes based on different risk-avoiding levels. The result shows that integrated strategies can enhance retirees’ well-being by 25%-50% for low/moderate levels of risk aversion when compared to full annuitization at retirement. Finally, we examined how welfare changes if the consumer is permitted to switch to a fixed annuity at an optimal point after retirement. This affords the retiree the chance to benefit from the equity premium when younger, and exploit the mortality credit in later life. For moderately risk-averse retirees, the optimal switching age lies between 75 and 80. asset allocation; annuitization; retirement policies 2016-05-03 国家社科基金(16BRK016);教育部人文社会科学青年基金(15YJC840037)。 王云多,男,黑龙江大学经济与工商管理学院副教授,博士,主要从事人口与劳动经济研究。 F832.21 A 1005-1007(2016)09-0027-10
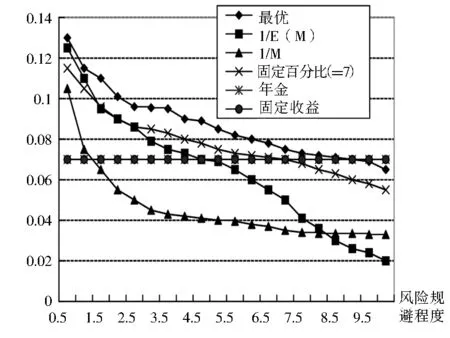
四、收益分配计划的效用分析






五、结语
