内置CFRP圆管的方钢管混凝土角柱节点有限元分析*

魏　华， 张赛茁

(沈阳工业大学 建筑与土木工程学院， 沈阳 110870)



内置CFRP圆管的方钢管混凝土角柱节点有限元分析*

魏华， 张赛茁

(沈阳工业大学 建筑与土木工程学院， 沈阳 110870)

为了分析内置CFRP圆管的方钢管混凝土角柱节点在往复载荷作用下的力学性能，以及不同的材料属性对节点力学性能的影响，利用ABAQUS有限元分析软件建立了10个角柱节点模型，分析钢材强度、含钢率和轴压比等参数对节点力学性能的影响.结果表明，随着钢材强度的提高，极限承载力有显著提高，含钢率对极限承载力和延性均有一定的改善，轴压比的增加使得极限承载力急剧下降，且延性变差.加强环宽度的增加对节点承载力有显著提高，达到70 mm之后有脆性破坏的趋势.

CFRP圆管； 方钢管； 加强环； 角柱节点； 往复载荷； 力学性能； 滞回曲线； 有限元分析

随着钢管结构的应用越来越广泛，钢管混凝土结构也取得了新的突破，两者结合以独特的优势为很多建筑工程提供了良好的经济效益与建筑效果.新型的复合材料——碳纤维增强塑料(carbon fiber reinforced polymer，CFRP)由于具有高强度、轻质量和耐腐蚀等特点，目前在建筑行业内得到了广泛的应用.

一般应用CFRP有两种形式，一种是钢管外壁包裹CFRP，提高钢管整体稳定性；另一种是钢管混凝土内置CFRP[1]，该方法不仅能够有效提高混凝土的延性和变形能力，提高方钢管的约束效果，还可以有效减轻结构自重，降低了钢材的消耗.目前对CFRP应用的研究[2]也越来越多.

梁与柱之间的节点是框架结构设计中的关键部位，在施工过程中也是难点，节点的作用主要是将梁端的弯矩、剪力传递给柱.节点形式的选择决定着梁柱间的内力传递与力矩的分配形式，进而直接影响着结构的安全性与稳定性[3].因此，弄清组成节点各组件的工作原理，探讨合理的节点连接方式，在研究钢管混凝土结构适用性与安全性领域具有十分重要的意义与价值.

近几年，研究人员对内置CFRP圆管的方钢管高强混凝土构件进行了系统的轴压短柱、中长柱、长柱、纯弯构件、偏压短柱、偏压中长柱等试验[4-7]，对于内置CFRP圆管的方钢管高强混凝土柱梁节点问题的研究起步较晚[8-10]，研究相对滞后，理论尚不完善，此领域还处于空白阶段.

1　模型建立

1.1模型的验证

本文建立的3个中柱节点模型JD-05、JD-01、JD-04与文献[7]中CJD-05、CJD-01、CJD-04节点模型分别考察钢材强度在235、310和390 MPa时节点的力学性能，节点模型如图1所示.

图1　中柱节点模型Fig.1　Model for middle column joint

对其梁端进行循环往复荷载作用，通过计算得到梁端滞回曲线对比如图2所示，p-Δ骨架曲线对比如图3所示.由滞回曲线可以看出，本文模拟3个节点与文献[7]中3个节点的滞回曲线形状基本一致，饱满度略差，这是由于考虑了钢管和混凝土接触界面的粘结滑移.从骨架曲线可以看出，各位移点对应的荷载值相差不大，经计算除个别点的荷载误差达到20%以外，其余均控制在2%～16%之内，说明吻合较好，因此，本文采用的有限元方法比较合理.

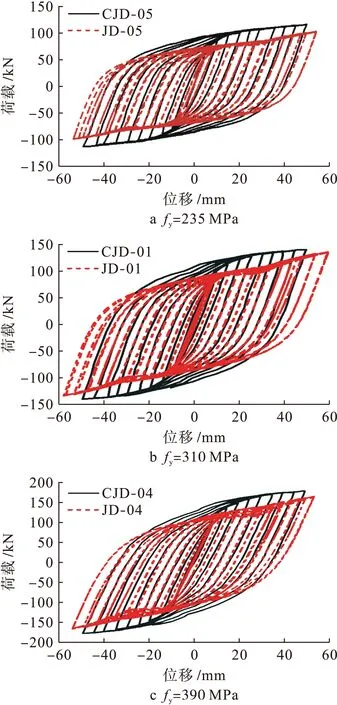
图2　滞回曲线对比Fig.2　Comparison in hysteresis curves

中柱节点的尺寸为柱高1 500 mm，截面尺寸为200 mm×200 mm，钢管壁厚8 mm，内填C80混凝土，CFRP的直径为125 mm，厚度为0.167 mm.梁的尺寸为H248 mm×124 mm×5 mm×8 mm，钢管与钢梁均选取Q235钢材.建立角柱节点模型，如图4所示，X梁(前梁)和Z梁(右梁)均伸长774 mm.

对于节点模型，改变参数的节点分别按顺序进行编号，各模型具体尺寸见表1，加强环的详细尺寸见图5(单位：mm).

1.2材料的本构关系

1) 钢材的本构关系.本文利用ABAQUS软件进行分析时，钢材采用的是简化后的双折线模型，如图6所示，屈服后的弹性模量取初始弹性模

图3　骨架曲线对比Fig.3　Comparison in skeleton curves

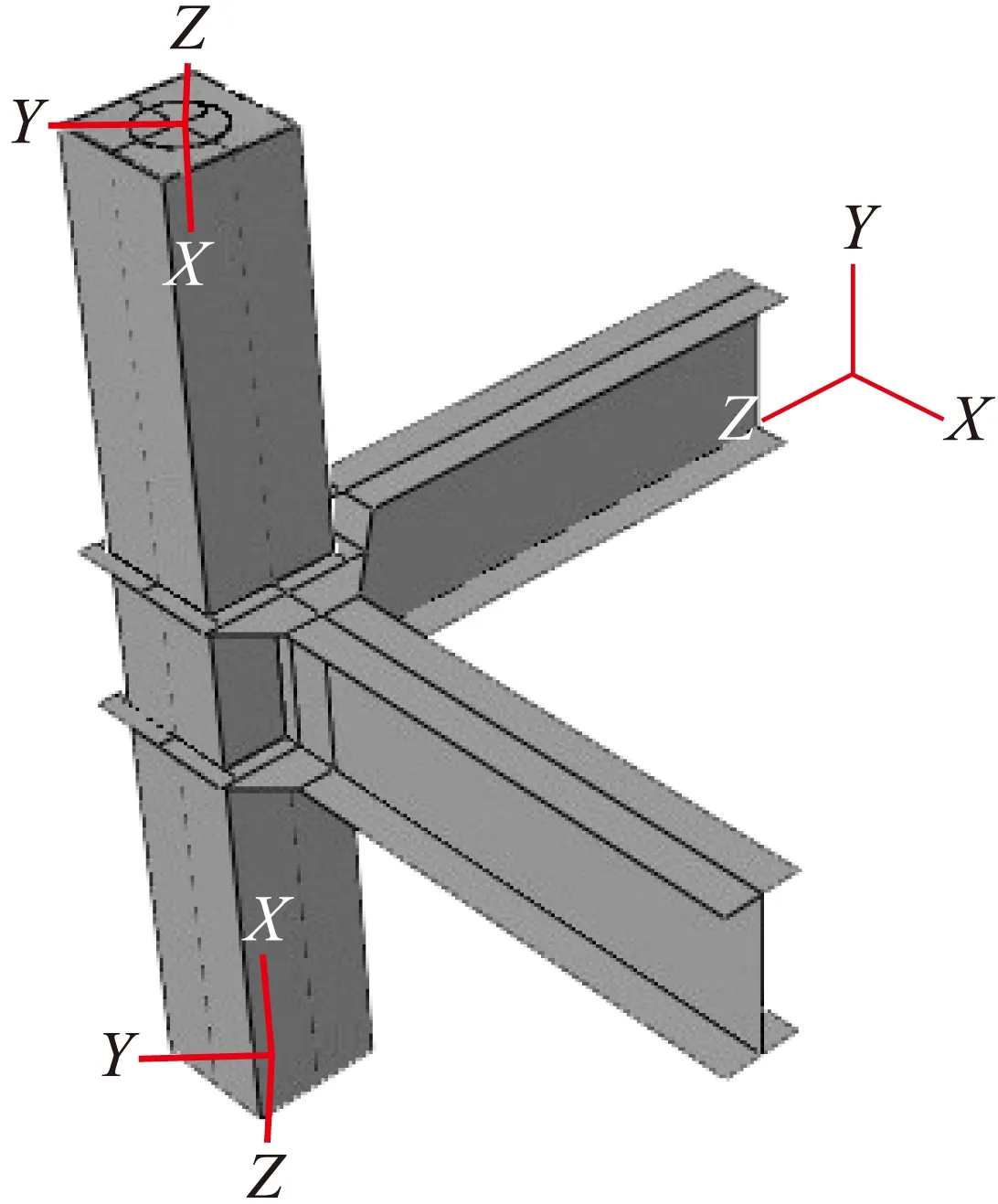
图4　角柱节点模型Fig.4　Model for corner joint

量Es的0.01倍，极限应变εu可由钢材的弹性模量Es、极限抗拉强度fu以及屈服强度fy计算得到，其表达式为

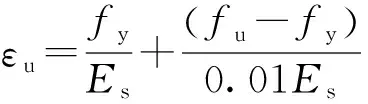
　　(1)表1　模型尺寸Tab.1　Model size

注：r为钢管厚度；fy为钢材屈服强度；n为轴压比；b为加强环翼缘宽度.

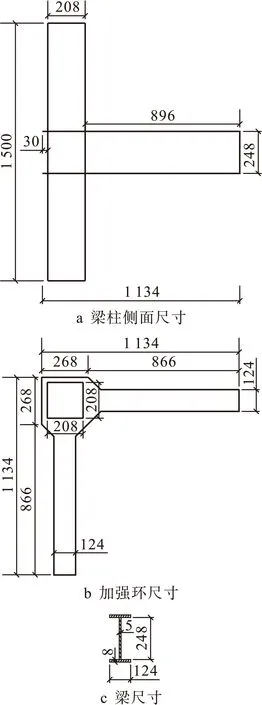
图5　加强环节点尺寸Fig.5　Size of joint with stiffening ring

2) 混凝土的本构关系.混凝土采用的是韩林海[11]提出的用“约束效应系数ξ”来阐述钢管与混凝土之间组合作用的本构模型，具体本构关系公式如下：

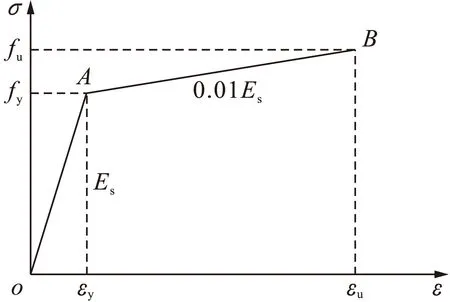
图6　钢材应力应变关系Fig.6　Relationship between stress and strain for steel

夹层混凝土本构关系为

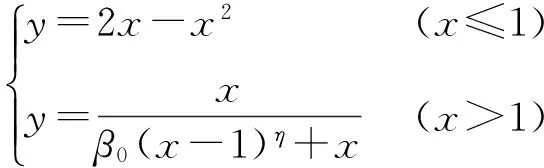
(2)

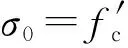
核心混凝土本构关系为

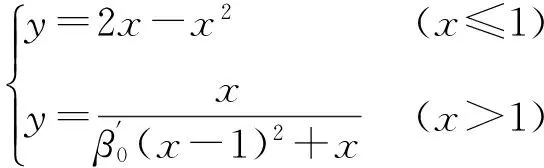
(3)

3) CFRP本构关系.CFRP材料具有很强的抗拉强度，在开裂前处于弹性阶段，断裂之后不再受荷，因此满足胡克定律，其表达式为

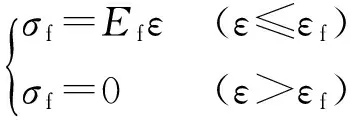
(4)

式中：Ef为CFRP材料的弹性模量；εf为其屈服应变.

1.3材料单元的选取

1) 钢材模型采用shell单元，选取四节点减缩积分(S4R)，Simpson积分取值为7个积分点.考虑到包辛格效应，钢材选用随动强化模型，弹性模量取206 000 MPa，泊松比取0.3.

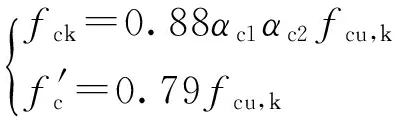
(5)

混凝土等级为C80时，αc1、αc2取值分别为0.82、0.87.

3) CFRP圆管采用shell单元，选取四节点减缩积分(S4R)，Simpson积分取值为3个积分点.选用复合材料单元(composite)，弹性模量取240 000 MPa.

1.4接触设置

1) CFRP与混凝土.根据参考文献[12]的结果可知，在整个受力过程中，CFRP始终附在夹层混凝土与核心混凝土中间协同工作，本文采用绑定约束(tie)的接触关系.

2) 混凝土与钢管.夹层混凝土与钢管之间的接触可以采用法线方向硬接触(hard contact)以及切线方向库伦摩擦(Penalty)模型.根据文献[13]，摩擦系数μ取0.6较为合适.

3) 钢管与钢梁.接触面可设置为绑定约束(tie)的关系，由于钢梁在模型中采用shell单元建模，所以选择“node to surface”模式进行绑定更合理.

1.5加载制度

对节点边界的加载方式一般有梁端加载和柱端加载两种，考虑到p-Δ效应，柱端加载更能贴近实际情况，因此本文采取柱端加载方式[14].将柱顶面耦合到一点Rp5，step1中对Rp5点施加轴力N，梁端处于水平可移动状态；step2中在Rp5点施加Z向的位移荷载，根据单调加载确定屈服位移Δy为10 mm，在屈服位移之前按0.25Δy、0.5Δy、0.75Δy加载，各循环1次，达到屈服位移之后按Δy、2Δy、3Δy、…、6Δy加载，各循环3次，加载制度如图7所示.

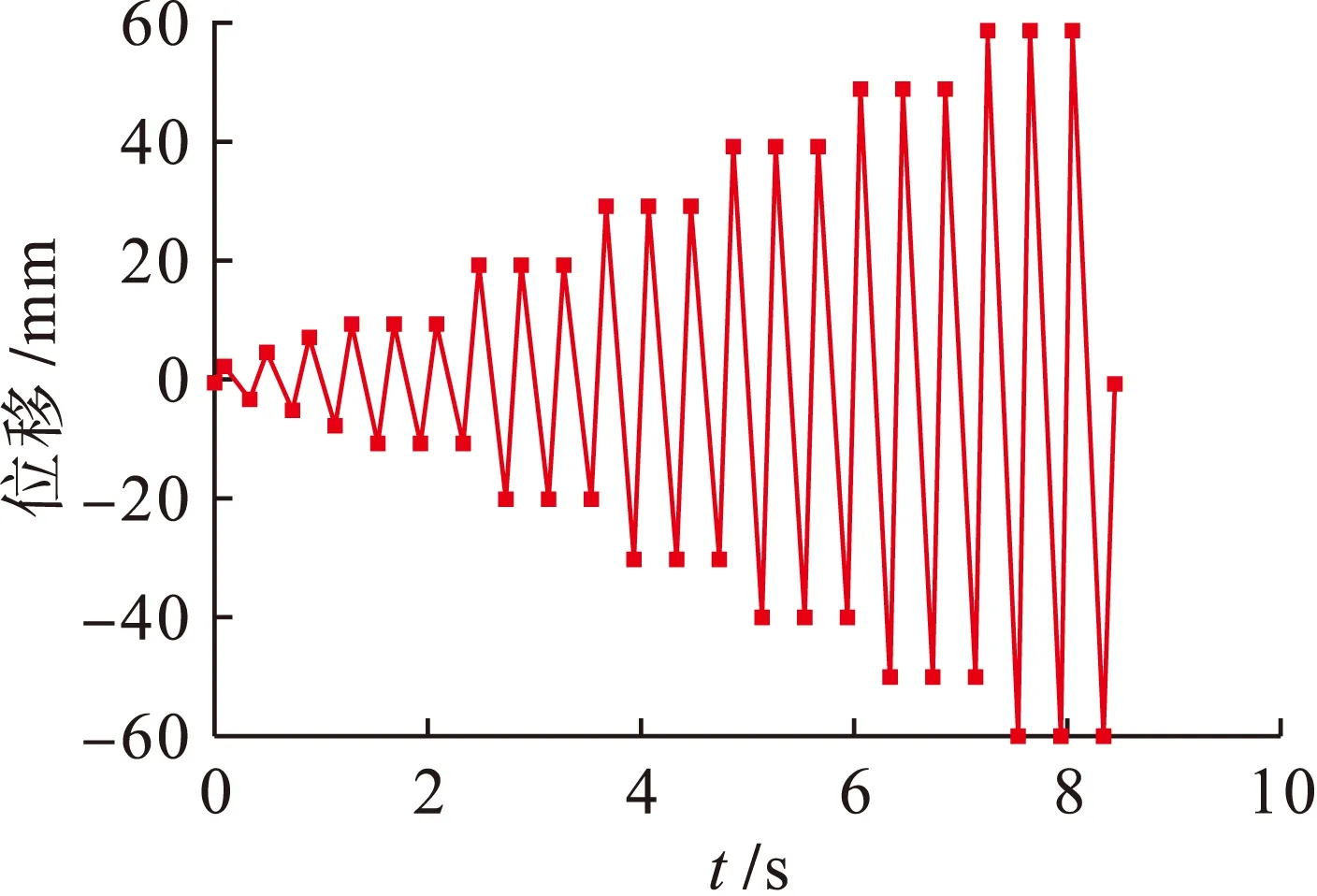
图7　加载制度Fig.7　Loading system

角节点模型的网格划分如图8所示.边界条件如下：柱顶和柱底设置为铰接，柱顶约束X和Y方向线位移，释放X轴的转动约束，柱底约束X、Y和Z方向线位移，释放X轴的转动约束.梁端设置为铰接，X梁约束Y和Z方向线位移，释放Z轴的转动约束，Z梁约束X和Y方向线位移，释放X轴的转动约束.

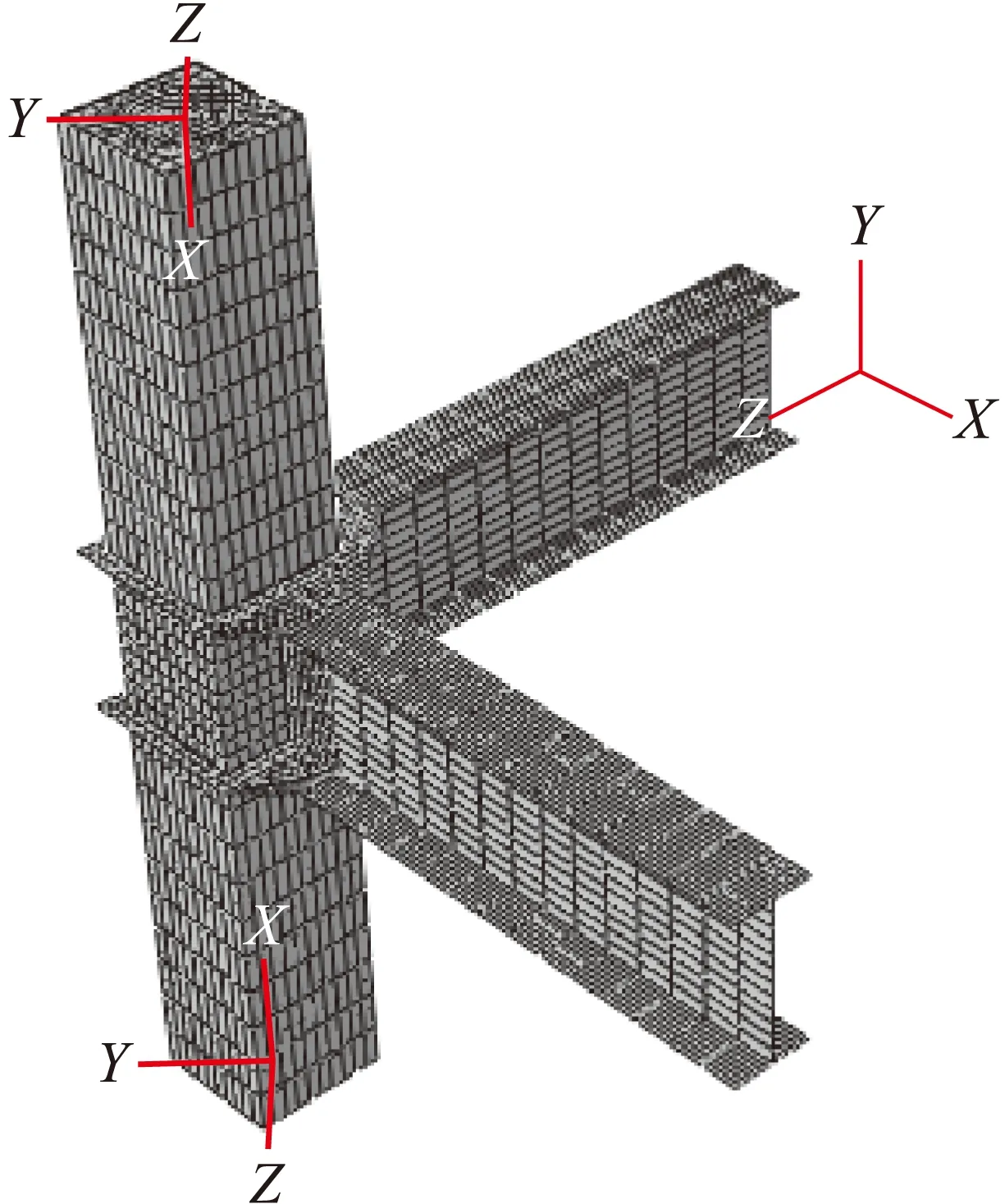
图8　模型网格划分Fig.8　Mesh division of model

2　模型计算结果

利用ABAQUS软件建立了10个角柱节点模型，通过改变钢材强度、含钢率、轴压比等参数，分析了各参数变化对节点骨架曲线、刚度退化以及强度退化等力学性能的影响.

2.1钢材强度的影响

钢材强度取235、310和390 MPa为参数变化，节点编号分别为JD-02、JD-01和JD-03，通过计算得出三者骨架曲线对比如图9所示.由图9可以看出，随着钢材强度的提高，节点的承载力有显著提高.

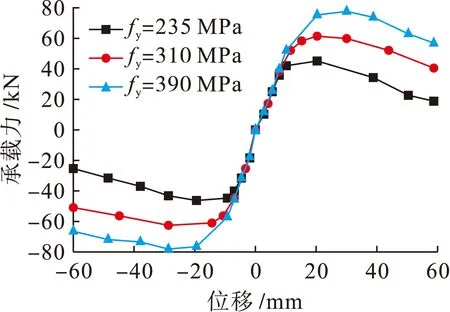
图9　不同钢材强度骨架曲线对比Fig.9　Comparison in skeleton curves with different steel strengths

刚度退化对比如图10所示，为便于分析，刚度退化对比图横坐标取无量纲化的Δ/Δy，纵坐标采取无量纲化的Kj/K1，其中，Δy为屈服位移，K1为第1级加载时的初始刚度.由图10可以看出，随着钢材强度的增大，节点的刚度退化有所延缓.

图10　不同钢材强度刚度退化对比Fig.10　Comparison in stiffness degradation with different steel strengths

强度退化对比如图11所示，强度退化对比图横坐标取无量纲化的Δ/Δy，纵坐标为承载力系数λj.由图11可以看出，钢材强度的增大能从一定程度上抑制节点强度的退化，作用不是很明显.

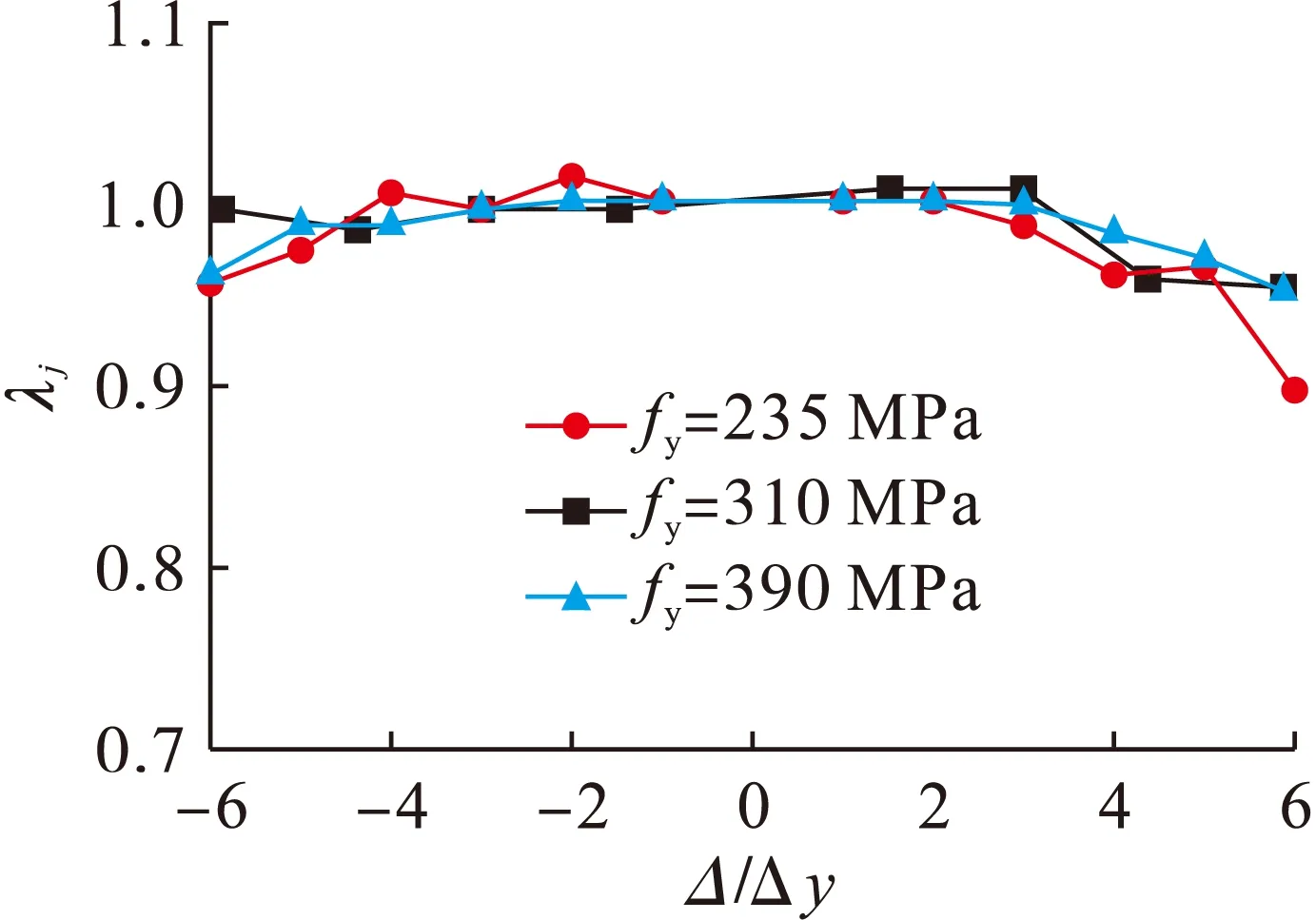
图11　不同钢材强度强度退化对比Fig.11　Comparison in strength degradation with different steel strengths

具体承载力与延性系数对比如表2所示.由表2可以看出，钢材强度的提高使得延性系数逐渐增大，变形能力得到了提高.

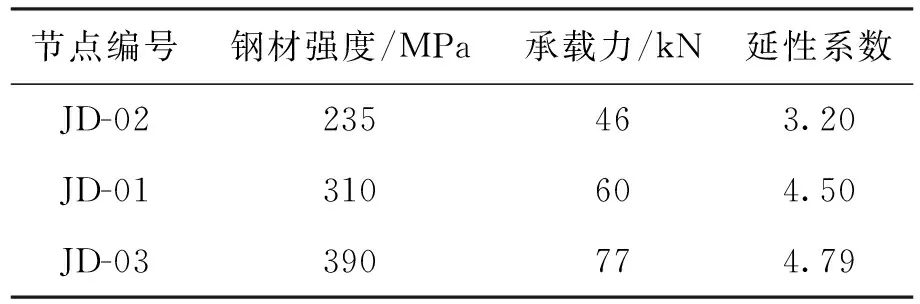
表2　不同钢材强度承载力及延性系数对比Tab.2　Comparison in bearing capacity and ductility coefficients with different steel strengths

2.2含钢率的影响

钢管厚度分别取6、8和10 mm，其含钢率分别为12.6%、17.36%和22.4%，节点编号分别为JD-04、JD-01、JD-05，通过计算得出三者骨架曲线对比如图12所示，由图12可以看出，随着含钢率的提高，极限承载力有显著提高，这是由于套箍系数越大，钢管对夹层混凝土的约束作用就越强，钢管厚度取10 mm时承载力最高.

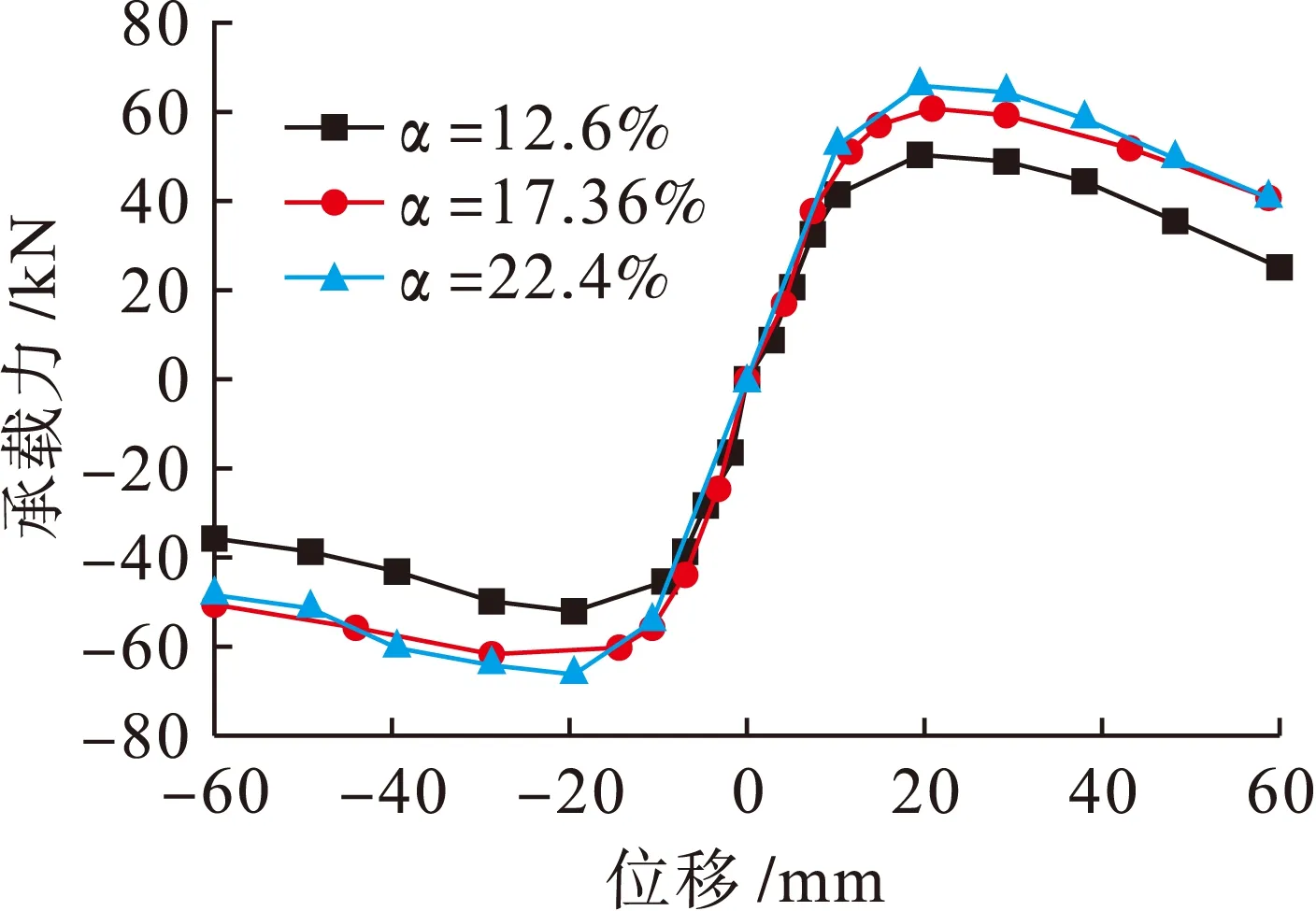
图12　不同含钢率骨架曲线对比Fig.12　Comparison in skeleton curves with different steel ratios

刚度退化对比如图13所示，可以看出含钢率的变化对节点刚度退化的影响还不是很明显，相对而言，钢管厚度为8 mm的节点刚度退化较慢.

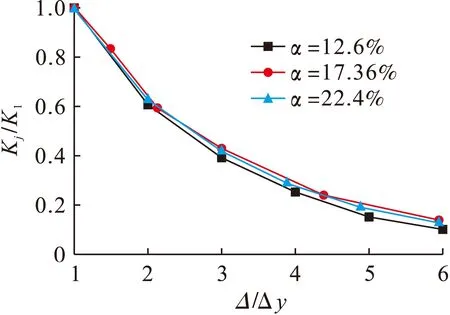
图13　不同含钢率刚度退化对比Fig.13　Comparison in stiffness degradation with different steel ratios

强度退化对比如图14所示，可以看出反向加载阶段各节点的强度退化现象基本一致，正向加载阶段后期含钢率12.6%的节点可能已经破坏，有强度增强的假象，含钢率22.4%的节点在加载后期强度显著下降.

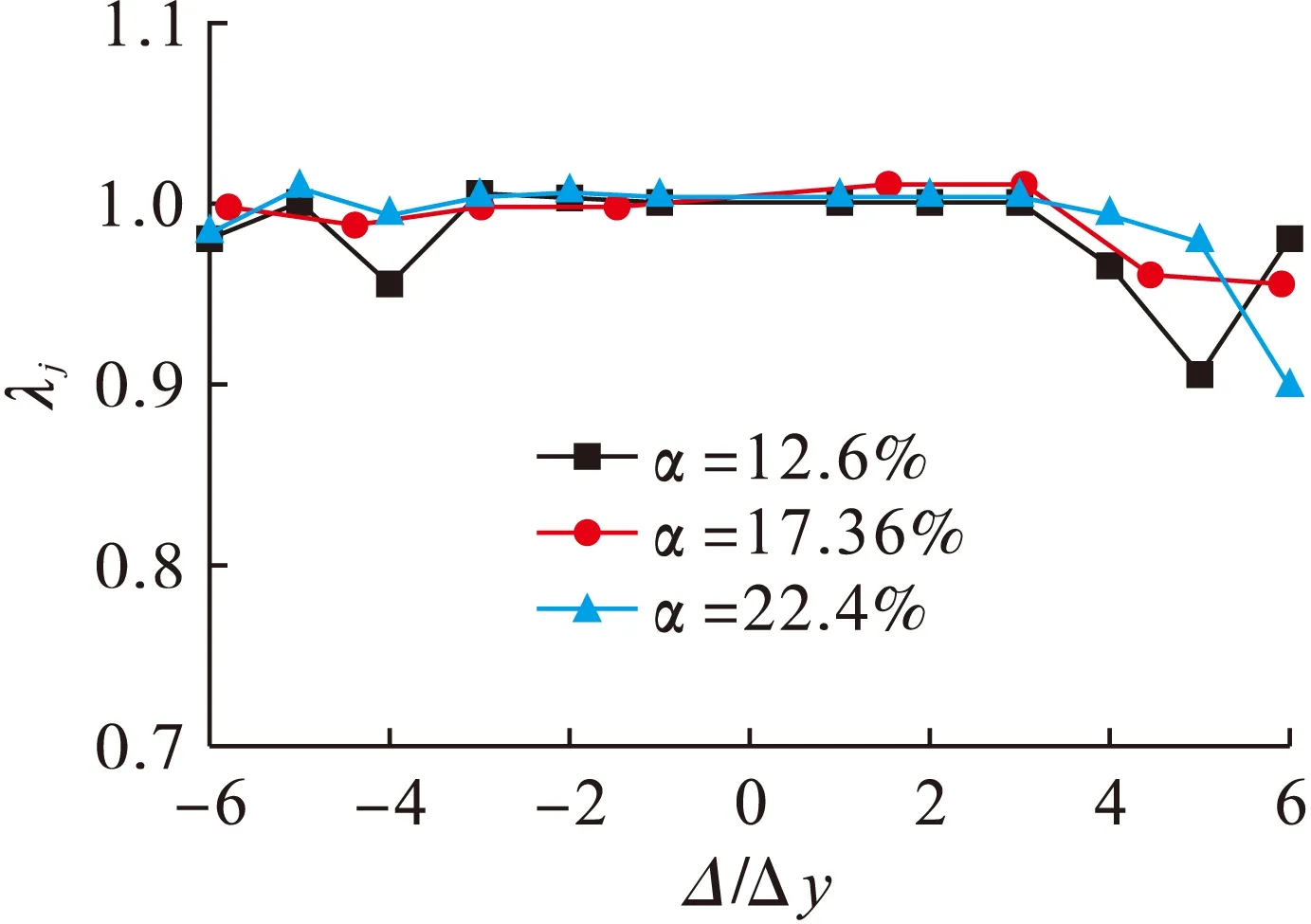
图14　不同含钢率强度退化对比Fig.14　Comparison in strength degradation with different steel ratios

具体承载力与延性系数对比如表3所示，可以看出，随着钢管厚度的增加，柱截面含钢率提高，极限承载力有所提高，位移延性系数降低，且降低幅度变小.

表3　不同含钢率承载力及延性系数对比Tab.3　Comparison in bearing capacity and ductility coefficients with different steel ratios

2.3轴压比的影响

极限承载力Nu根据相关规范给出的公式可以计算得出，方、矩形钢管混凝土相关计算公式为

(6)

式中：Asc为钢管混凝土柱截面面积；fscy是由套箍系数和混凝土抗压强度标准值确定的一个参数值；ξ为混凝土受到钢管与CFRP管的双重约束作用的套箍系数.根据轴压比的定义n=N0/Nu，作用在柱顶中心恒定的竖向荷载N0亦可得出.

轴压比分别取0.2、0.3、0.4和0.6，根据式(6)计算对应的柱端轴向力分别为982.6、1 474、1 965和2 947.8 kN，节点编号分别为JD-06、JD-01、JD-07和JD-08，通过计算得出骨架曲线如图15所示.可以看出，随着轴压比的增加，骨架曲线下降较快，极限承载力明显下降，说明轴压比的增大使得极限承载力下降.

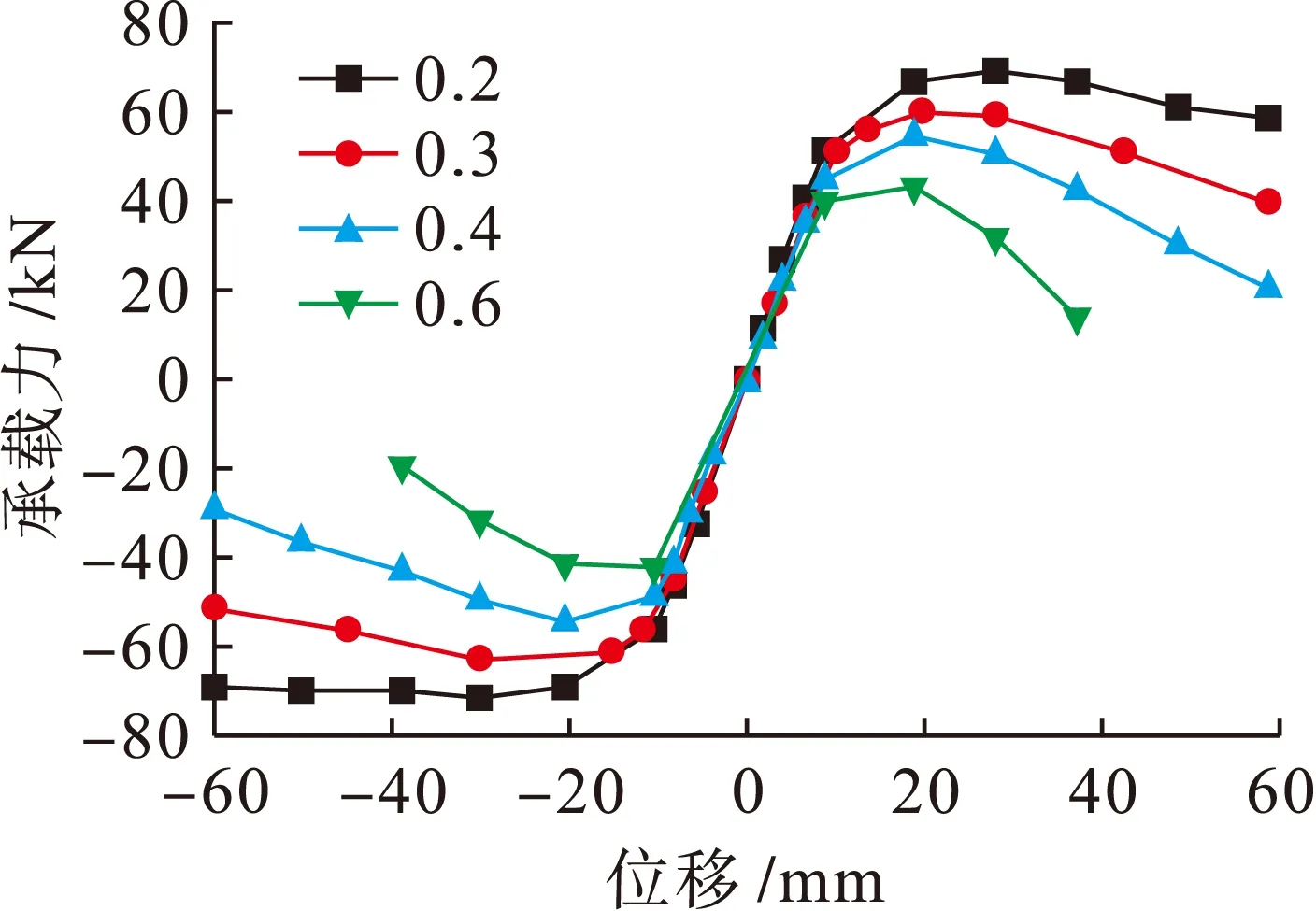
图15　不同轴压比骨架曲线对比Fig.15　Comparison in skeleton curves with different axial compression ratios

刚度退化对比如图16所示，可以看出刚度退化曲线变得越来越陡，尤其是轴压比取0.6时，节点的刚度退化较为严重.

强度退化对比如图17所示，可以看出，随着轴压比的增加，节点强度的退化速度加快.这是由于轴压比越大，施加的轴向力越大，达到极限荷载后，核心混凝土破坏，钢管开裂，导致节点强度急剧下降.

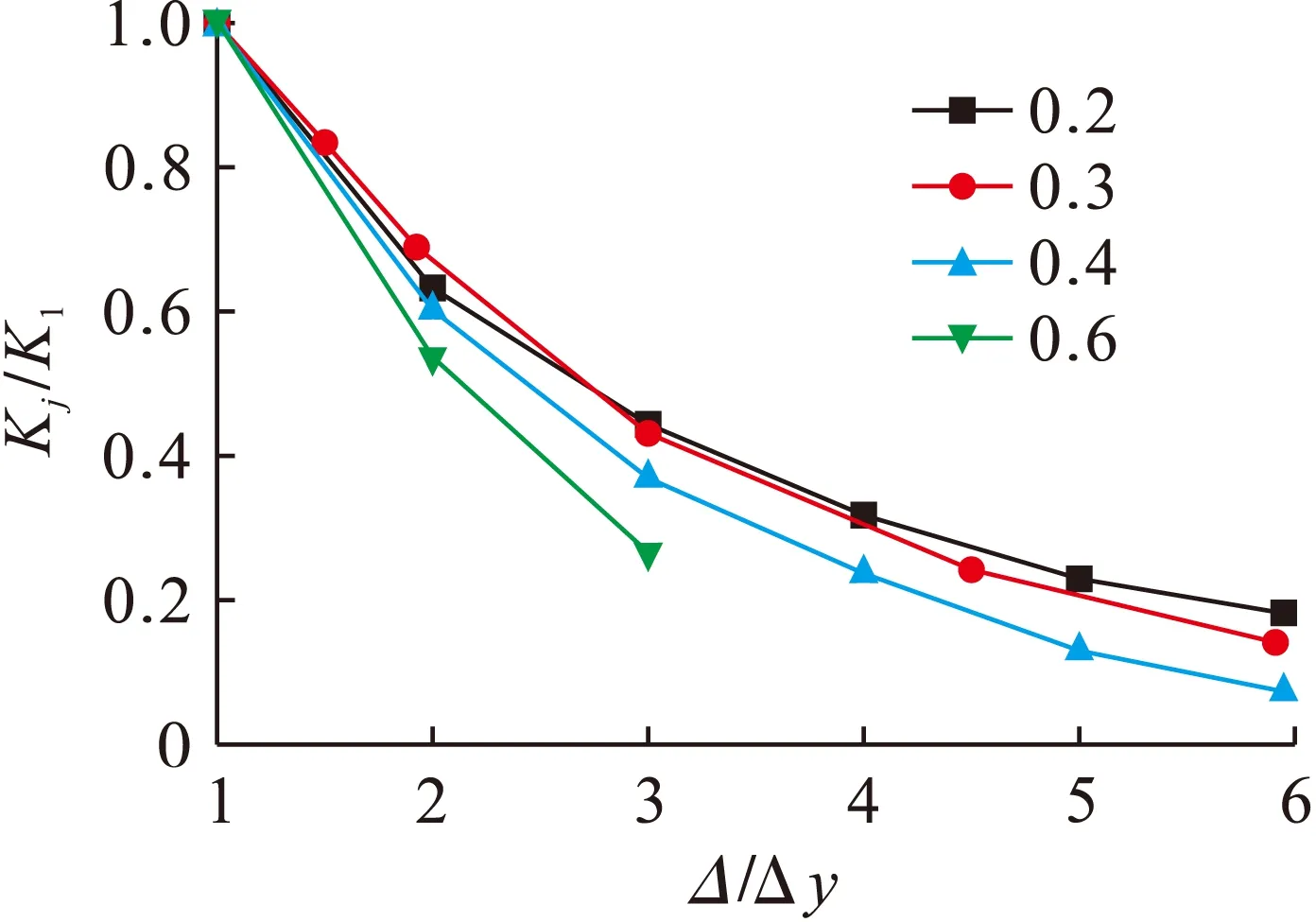
图16　不同轴压比刚度退化对比Fig.16　Comparison in stiffness degradation with different axial compression ratios

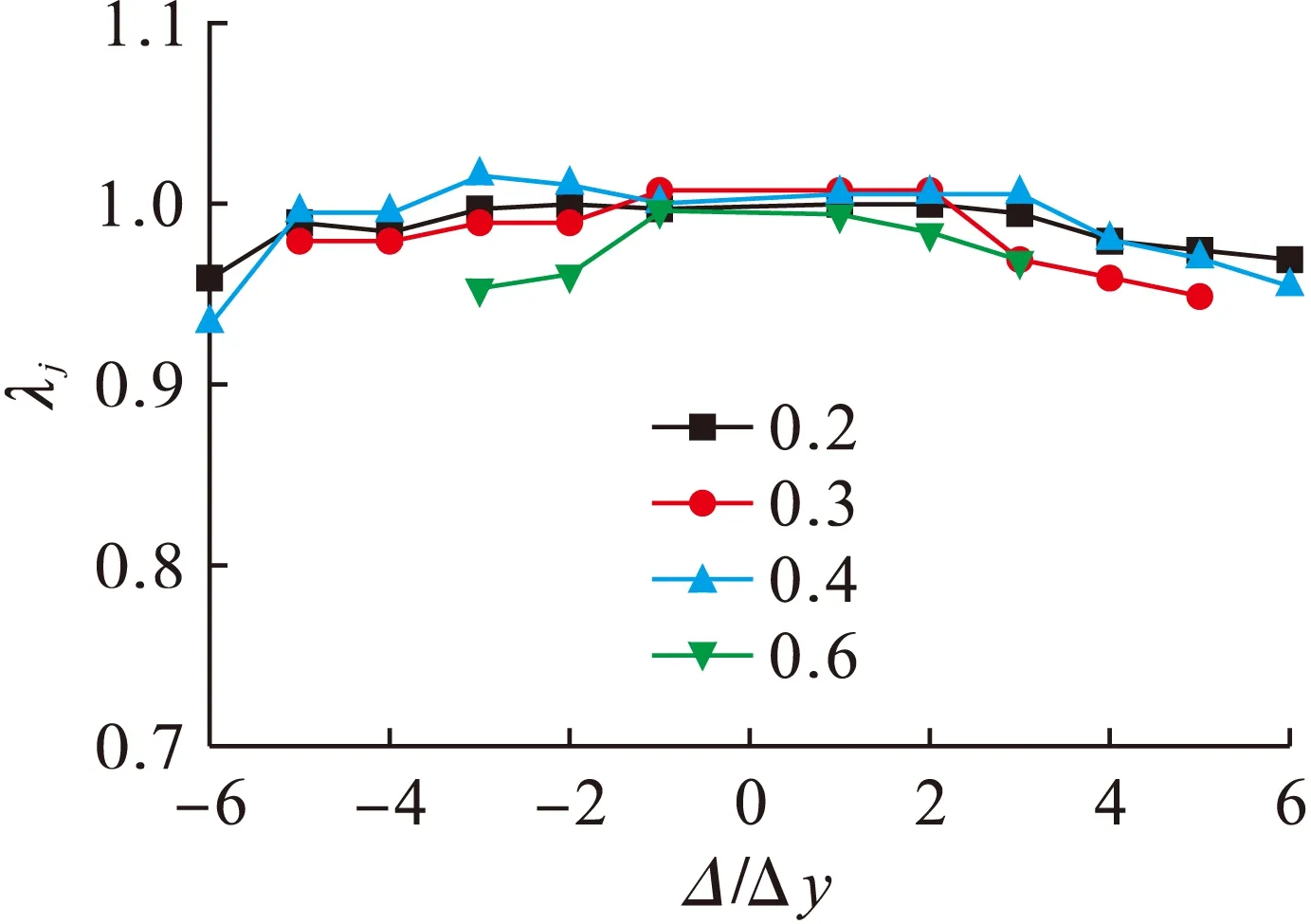
图17　不同轴压比强度退化对比Fig.17　Comparison in strength degradation with different axial compression ratios

具体承载力与延性系数对比如表4所示，可以看出，随着轴压比的增加，延性系数越来越小，变形能力变差.

表4不同轴压比承载力及延性系数对比

Tab.4Comparison in bearing capacity and ductility coefficients with different axial compression ratios

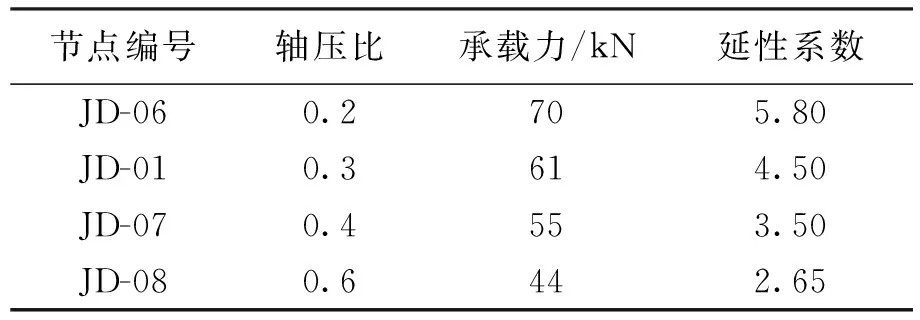
节点编号轴压比承载力/kN延性系数JD-060.2705.80JD-010.3614.50JD-070.4553.50JD-080.6442.65

2.4加强环宽度的影响

JD-09和JD-10分别是加强环宽50和70 mm的两个模型，与模型JD-01加强环宽30 mm形成对比，通过计算得出三者骨架曲线对比如图18所示，可以看出极限承载力有显著提高，达到峰值后急剧下降，有脆性破坏的趋势，且最终破坏荷载值大致相同.刚度退化对比如图19所示，可以看出加强环宽度的变化对节点的刚度退化基本无影响.强度退化对比如图20所示，可以看出随着加强环宽度的增加，节点的强度退化变得明显，且强度开始出现退化的位移变小，说明环板宽度大的节点较早地进入强度退化阶段.

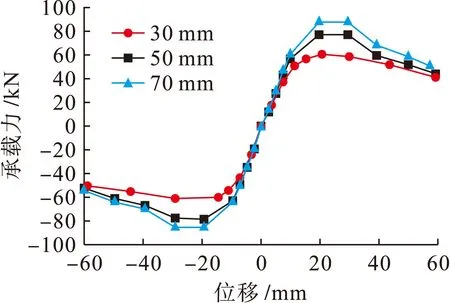
图18　不同加强环宽度骨架曲线对比Fig.18　Comparison in skeleton curves with different width of stiffening ring

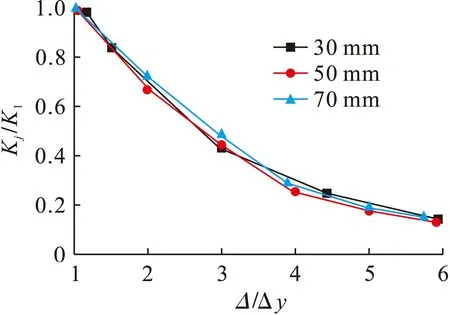
图19　不同加强环宽度刚度退化对比Fig.19　Comparison in stiffness degradation with different width of stiffening ring

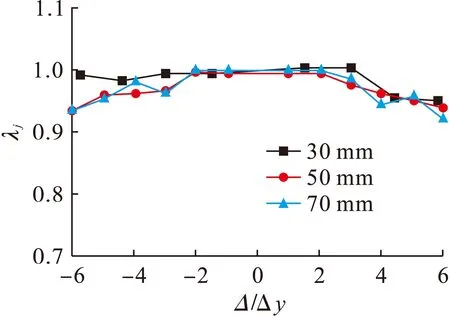
图20　不同加强环宽度强度退化对比Fig.20　Comparison in strength degradation with different width of stiffening ring

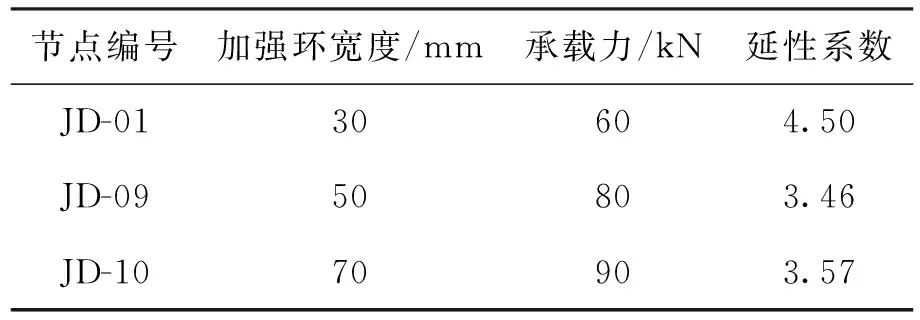
具体承载力与延性系数对比如表5所示.可以看出，随着加强环宽度的增加，极限承载力的提高较为显著，但是位移延性系数有所降低，节点的延性变差.因此在设计时，结构的延性与承载力要兼顾考虑，不能一味追求一方的最大化，避免给结构安全埋下隐患.

3　破坏过程

以JD-01为例，钢材强度为310 MPa，混凝土强度C80，钢管厚度为8 mm，轴压比为0.3，加强环宽度为30 mm，CFRP圆管直径为125 mm.各部

表5不同加强环宽度承载力及延性系数对比

Tab.5Comparison in bearing capacity and ductility coefficients with different width of stiffening ring

节点编号加强环宽度/mm承载力/kN延性系数JD-0130604.50JD-0950803.46JD-1070903.57

件在破坏位移时应力云图如图21所示，节点域的变形如图22所示.

由图21、22可以看出，节点的破坏首先发生在与梁翼缘连接的加强环变截面处，钢材屈服发生局部屈曲，且屈服面积随着荷载的增大逐渐变大，导致与加强环连接的腹板位置的钢材也进入屈服阶段.方钢管柱壁的受力高度随着荷载的增加逐渐提高，且趋于一定的范围不再扩大.核心混凝土的应力云图呈现鸡蛋形.夹层混凝土的受力主要集中在与腹板连接面的加强环高度处，在方钢管角部位置有应力集中现象.CFRP在加载初期受荷均匀，加载后期也呈现出鸡蛋形，由于CFRP对核心混凝土的约束作用，使得加载后期核心混凝土的应力值要高于夹层混凝土.

4　结　论

本文通过分析得出以下结论：

1) 随着钢材强度的增加，极限承载力显著提高，能一定程度上延缓节点的刚度退化和强度退化，延性性能得到改善.这是由于钢材强度的提升对混凝土的约束作用明显加强，能够更好地发挥塑性性能.

2) 钢管厚度由6、8 mm增加到10 mm，随着含钢率的提高，极限承载力随之大幅度增加，延性及刚度退化没有相应的改善，厚度为8 mm时延性系数最高，变形能力最好.这是由于含钢率越高，套箍系数就越大，钢管对夹层混凝土的约束作用就越强，能有效地提升节点的极限承载力.

3) 随着轴压比的增大，极限承载力显著下降，刚度退化以及强度退化都比较明显.由于采用柱端加载方式，所以轴压比的变化对柱端滞回曲线影响较大，本文轴压比取值为0.2、0.3、0.4和0.6，在此范围内，轴压比越大，越早进入屈服阶段，且极限承载力变得越低，延性性能变得越差.

4) 随着加强环宽度的增加，节点极限承载力有显著提高，延性性能变差，且刚度退化和强度退

图21　应力云图Fig.21　Stress nephogram

图22　节点破坏变形Fig.22　Damage deformation of joints

化现象变得明显.对于本文模拟的加强环宽度为30、50和70 mm的节点，后两者节点有脆性破坏的趋势，因此在设计时，结构的延性与承载力要兼顾考虑，不能一味追求一方的最大化.

5) 节点破坏出现在与梁翼缘连接的外加强变截面处，属于梁端塑性铰破坏，符合“强柱弱梁”的原则.

[1]李帼昌，张春雨，于洪平.内置CFRP圆管的方钢管高强混凝土结构研究进展 [J].工程力学，2012，29(增刊2)：57-68.

(LI Guo-chang，ZHANG Chun-yu，YU Hong-ping.Advance in high-strength concrete filled square steel tubular structure with inner CFRP circular tube [J].Engineering Mechanics，2012，29(Sup2)：57-68.)

[2]杜闯，李艳艳，宋倜.预应力CFRP布三种粘贴方式对RC梁受弯性能的影响 [J].沈阳工业大学学报，2014，36(4)：464-470.

(DU Chuang，LI Yan-yan，SONG Ti.Influence of three bonded ways for prestressed CFRP sheet on fle-xural properties of RC beams [J].Journal of Shen-yang University of Technology，2014，36(4)：464-470.)

[3]蔡健，黄泰赟.钢管混凝土柱节点的应用现状和存在问题 [J].建筑结构，2001，31(7)：8-10.

(CAI Jian，HUANG Tai-yun.Application status and problems of concrete-filled steel tube column joints [J].Building Structure，2001，31(7)：8-10.)

[4]李帼昌，邢娜，邢忠华.内置CFRP圆管的方钢管高强混凝土轴压短柱试验 [J].沈阳建筑大学学报(自然科学版)，2009，25(2)：244-249.

(LI Guo-chang，XING Na，XING Zhong-hua.Axial compression test on short column of high-strength concrete filled square steel tubular structure with inner CFRP circular tube [J].Journal of Shenyang Jianzhu University (Natural Science)，2009，25(2)：244-249.)

[5]李帼昌，麻丽，杨景利，等.内置CFRP圆管的方钢管高强混凝土轴压短柱承载力计算初探 [J].沈阳建筑大学学报(自然科学版)，2008，24(1)：62-66.

(LI Guo-chang，MA Li，YANG Jing-li，et al.Calculation of bearing capacity of high-strength concrete filled square steel tubular structure with inner CFRP circular tube under axial compression [J].Journal of Shen-yang Jianzhu University (Natural Science)，2008，24(1)：62-66.)

[6]李帼昌，石钧吉，杨志坚，等.内置CFRP圆管的方钢管高强混凝土中长柱轴压性能试验 [J].沈阳建筑大学学报(自然科学版)，2010，26(1)：47-51.

(LI Guo-chang，SHI Jun-ji，YANG Zhi-jian，et al.Axial compression test on middle long column of high-strength concrete filled square steel tubular structure with inner CFRP circular tube [J].Journal of Shen-yang Jianzhu University (Natural Science)，2010，26(1)：47-51.)

[7]李帼昌，李淑杰，王奇.内置CFRP圆管的方钢管高强混凝土短柱的非线性有限元分析 [J].沈阳建筑大学学报(自然科学版)，2011，27(3)：451-456.

(LI Guo-chang，LI Shu-jie，WANG Qi.Nonlinear finite element analysis on short column of high-strength concrete filled square steel tubular structure with inner CFRP circular tube [J].Journal of Shenyang Jianzhu University (Natural Science)，2011，27(3)：451-456.)

[8]蒋奇峰.内置CFRP圆管方钢管高强混凝土节点受力性能有限元分析 [D].沈阳：沈阳建筑大学，2011.

(JIANG Qi-feng.Finite element analysis on mechanical behavior of joint of high strength concrete-filled square steel tube with inner CFRP circular tube [D].Shenyang：Shenyang Jianzhu University，2011.)

(LIU Yu.Finite element analysis on high-concrete filled square steel tubular column with inner CFRP circular tube and steel beam [D].Shenyang：Shenyang Jianzhu University，2012.)

(LI Guo-chang，LI Dong-hui，LIU Yu.Static analysis of joints between high-concrete filled square steel tubular column with inner CFRP circular tube and steel beam [J].Journal of Shenyang Jianzhu University (Natural Science)，2014，30(3)：442-449.)

(HAN Lin-hai.Concrete filled steel tubular structure-theory and practice [M].Beijing：Science Press，2007.)

(LANG Yan，YANG Zhi-jian，LI Ze-liang.Failure analysis and ductillity optimization of CFSST stub co-lumn with inner CFRP tube under axial compressive load [J].Journal of Civil，Architectural & Environmental Engineering，2014，36(4)：22-27.)

[13]刘威.钢管混凝土局部受压时的工作机理研究 [D].福州：福州大学，2005.

(LIU Wei.Research on mechanism of concrete-filled steel tubes subjected to local compression [D].Fuzhou：Fuzhou University，2005.)

[14]马超.T形钢管混凝土柱——钢梁框架边柱外加强环节点抗震性能研究 [D].荆州：长江大学，2012.

(MA Chao.Experimental research on seismic behavior of exterior frame joints with T-shaped CFST column and steel beam [D].Jingzhou：Yangtze University，2012.)

(责任编辑：钟媛英文审校：尹淑英)

Finite element analysis for corner joints of concrete filled square steel tube with inner CFRP circular tube

WEI Hua, ZHANG Sai-zhuo

(School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China)

In order to study the mechanical properties of corner joints of concrete filled square steel tube with inner CFRP circular tube under the action of cyclic loads and the effect of different material attributes on the mechanical properties of the joints, ten models for the corner joints were established with ABAQUS finite element analysis software, and the influence of such parameters as steel strength, steel ratio and axial compression ratio on the mechanical properties of the joints was analyzed. The results show that with increasing the steel strength, the ultimate bearing capacity can be significantly improved. The ultimate bearing capacity and ductility can be improved by the steel ratio. With increasing the axial compression ratio, the ultimate bearing capacity significantly reduces, and the ductility becomes poor. The bearing capacity can be significantly improved by increasing the width of stiffening ring, but there will be a tendency of brittle failure when the width reaches 70 mm.

CFRP circular tube; square steel tube; stiffening ring; corner joint; cyclic load; mechanical property; hysteresis curve; finite element analysis

2015-10-09.

沈阳市科技计划项目(F13-316-1-43).

魏华(1973-)，女，山西交城人，副教授，博士，主要从事结构工程等方面的研究.

10.7688/j.issn.1000-1646.2016.04.19

TU 398.9

A

1000-1646(2016)04-0467-09

*本文已于2016-03-02 16∶45在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20160302.1645.026.html