考虑不可行路径的逆向物流回收路径问题*

刘艳秋， 吴　蒙， 徐世达

(沈阳工业大学 理学院， 沈阳 110870)



考虑不可行路径的逆向物流回收路径问题*

刘艳秋， 吴蒙， 徐世达

(沈阳工业大学 理学院， 沈阳 110870)

针对车辆回收路径问题的研究较少考虑部分节点可被多次访问的情况，以及现实生活中无法保证可行的直线路径均存在的问题，建立了以逆向物流网络最低总运输成本为优化目标的数学模型.通过FLOYD算法将问题转化为传统车辆路径问题模型，通过改进的蚁群算法进行求解，确定回收设施的数量和位置，并得到最优回收车辆路径.通过算例验证了模型和算法的有效性，对解决逆向物流路径问题具有一定的实际意义.

逆向物流； 回收路径； 不可行路径； 物流节点； 回收中心； 数学模型； FLOYD算法； 改进的蚁群算法

逆向物流回收路径问题(Vehicle routing problem in reverse logistics，VRPRL)是车辆路径问题(Vehicle routing problem，VRP)在逆向物流环境下的扩展问题研究.VRPRL是通过设计逆向物流网络并合理调配回收车辆以满足各个客户需求点的废弃物回收需求.传统的逆向物流网络模型中假设任意两个物流节点之间均存在可行的直线路径并且每个节点仅可被访问一次，而在现实生活中，无法保证可行的直线最短路径均存在.

高举红等[1]针对危险废弃物的回收路径问题，综合考虑回收成本与风险因素进行了研究；蒋忠中等[2]研究了考虑不可行路径的B2C电子商务物流的配送路径优化问题；梁春艳等[3]针对含有随机参数的废旧家电逆向物流路径规划问题，建立了面向对象的仿真模型；Tolga等[4]考虑了碳排放约束下的车辆路径问题；Kim等[5]研究了电子产品的车辆回收路径问题；Tang等[6]运用禁忌搜索算法和局部优化算法，求解了多节点情况下的最大行程约束车辆路径问题；李华俊[7]分析了逆向物流系统优化中回收中转站的选址、库存控制策略和收集车辆的路径选择三者之间的内在联系；任志刚[8]提出逆向物流网络选址运输问题求解首先要规划出回收站与回收中心之间最短路径，然后才可进行优化；刘艳秋等[9]提出了带能力约束的多级物流配送网络，并应用模拟退火算法思想进行求解.

1　问题描述与模型建立

自建物流情况下，车辆调度要求从回收中心发出的车辆完成回收任务后最终返回该回收中心.传统车辆路径问题模型所研究的物流网络模型假设网络中各个物流节点之间均存在可行的直线路径，并且每个物流节点只能被访问一次.而实际情况中，由于地理环境、运载条件等外界因素的限制，无法保证物流网络中物流节点间可行路径均存在.为了保证物流网络中所有客户的回收需求均能得到满足，回收车辆完成部分节点的回收任务后，沿着回收路径返回到某一个已访问节点，之后行驶向其他节点进行回收任务，则部分物流节点会出现被多次访问的情况.

根据实际情况中物流节点会出现多次被访问的情况，本文增加了对路径可行性与物流节点可被多次访问的情况建立数学模型.通过FLOYD算法[10]将问题转化为传统VRP模型，并通过改进的蚁群算法[11]进行求解.

设G={V，E}为一个由处理中心、回收站组成的不完全无向图，式中，V=S∪R，S为回收中心节点集合，R为回收站节点集合，E为两类物流节点间可行路径集合.模型可表示为

(1)

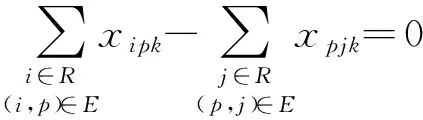
(∀p∈S，k∈Kp)

(2)

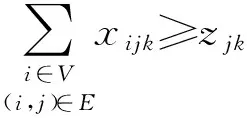
(3)

(4)

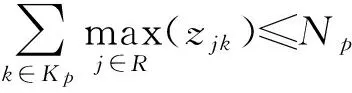
(5)

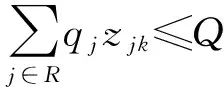
(6)

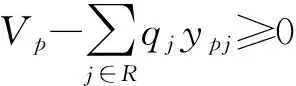
(7)

ωi≥yij(∀i∈S，j∈R)

(8)

xijk=0，1(∀i，j∈V，k∈K)

(9)

yij=0，1(∀i∈S，j∈R)

(10)

zjk=0，1(∀j∈R，k∈K)

(11)

ωi=0，1(∀i∈S)

(12)

式中：K为回收车辆集合；Kp为回收中心p的车辆集合；Np为回收中心p的车辆总数；Vp为回收中心的最大处理能力，即回收中心的容量；Mk为车辆k的调用费用；Fi为回收中心i的建设费用；cij、dij为路径(i，j)之间的单位运输费用和最短路程距离；qj为回收点j的废弃物总量；Q为车辆的最大载重量.

模型中的决策变量为

模型的目标函数第一部分是车辆的运输费用，第二部分是车辆的调用费用，第三部分是回收中心的建设费用；式(2)表示回收中心发出的车辆最终必须返回该回收中心；式(3)表示若j由k负责回收，则k至少访问j一次；式(4)表示每个待回收站仅由一辆车辆负责回收；式(5)表示每个回收中心车辆调用数限制；式(6)表示回收车辆的装载量不超过容量；式(7)表示回收中心可以处理所有调出车辆所回收的废弃物；式(8)确保回收中心用于回收任务时，该回收中心已经建立；式(9)～(12)为变量约束.

2　基于FLOYD算法的改进蚁群算法

传统蚁群算法无法对VRPRL中不可行路径与节点被多次访问情况进行表达和求解，因此，本文运用FLOYD算法思想对距离矩阵与信息素更新策略进行修改，并增加指针矩阵，将问题转化为传统VRP问题进行求解.

传统VRP问题研究的是一类完全图，任意两个物流节点间存在可行的直线路径，在蚁群算法中体现为距离矩阵D中的元素可以直接表达出任意两个物流节点的最短距离.而本文研究的是一类如图1所示的不完全网络图，图1所对应的距离矩阵D表示为

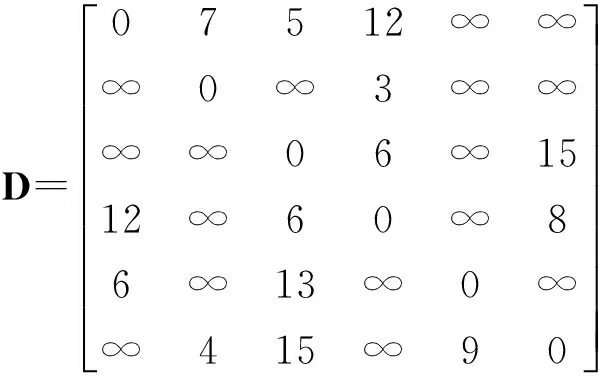
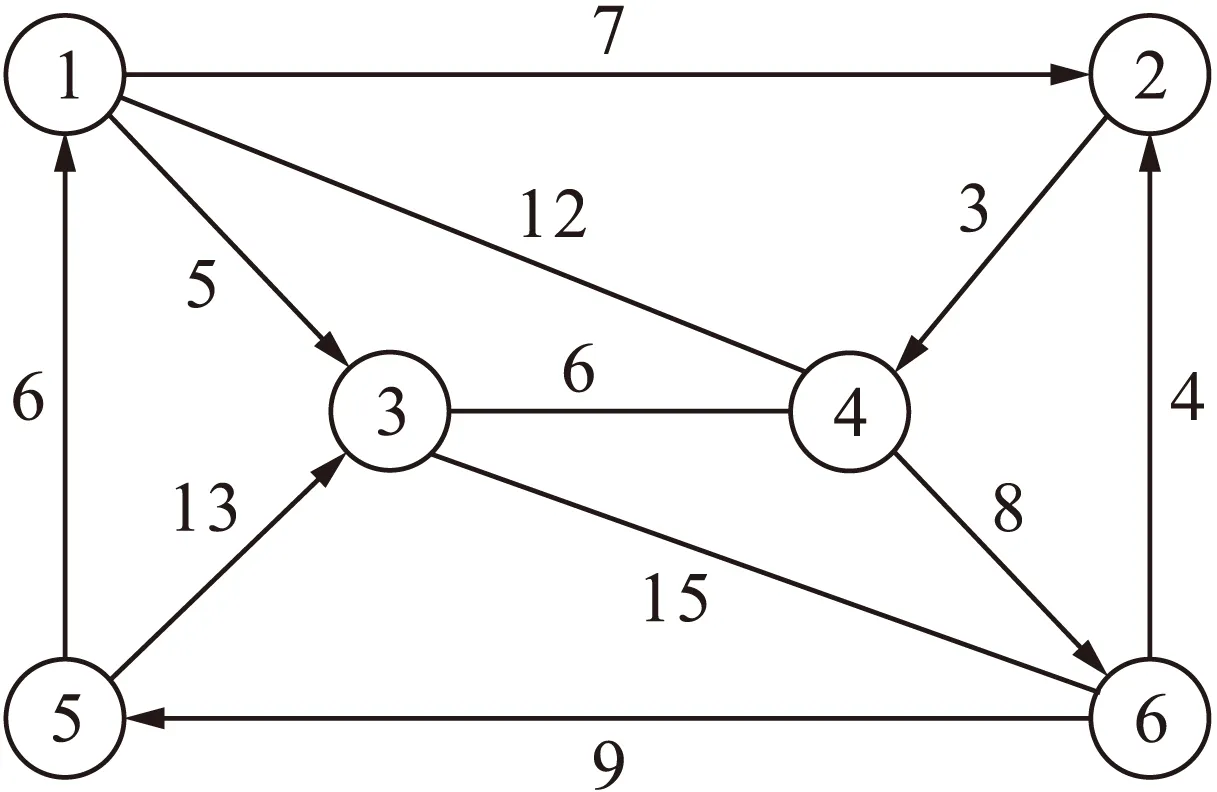
图1　网络结构图Fig.1　Network structure diagram

对于图中没有可行直线路径的两个物流节点，采用FLOYD算法求得最短路径与路径长度.FLOYD算法用于求解网络中任意两个点的最短距离，并可通过指针矩阵同步记录最短路径.通过该算法，问题转化为传统VRP问题，更新后的距离矩阵D′表示物流网络中任意两个节点的可行最短距离，指针矩阵P表示达到最短距离时的路径走向，其表达式分别为

3　仿真结果与比较分析

为了验证本文所提出数学模型与改进蚁群算法的有效性，运用改进前后的两种模型算法分别对VRP问题进行求解分析.随机产生3个处理中心，17个回收站，70个需求点的逆向物流回收网络.17个回收站将需求点部分废弃物回收后，3个回收中心的最大回收量以及各个回收站的待回收废弃物量如表1、2所示.

表1　回收中心最大回收量Tab.1　Maximum recycling amount in recycling center

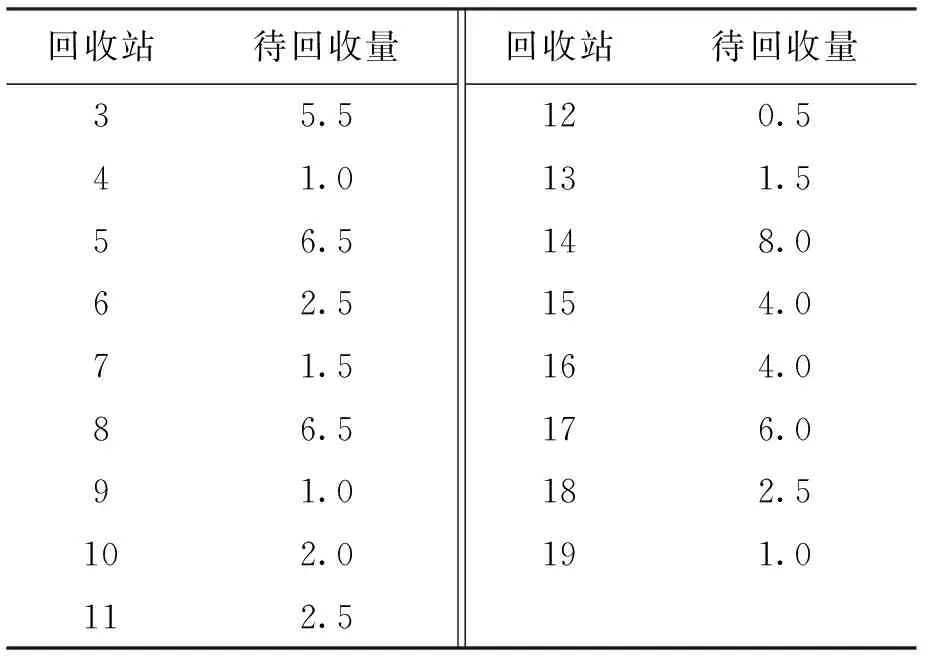
表2　回收站待回收量Tab.2　Recycling amount to be recycled in recycling stations

设回收中心可用车辆数Np=3，车辆最大载重Q=20 t，车辆调用费用Mk=500元，各条路径单位运输费用cij=7元，回收中心的运作费用均为5 000元，逆向物流回收网络如图2所示.

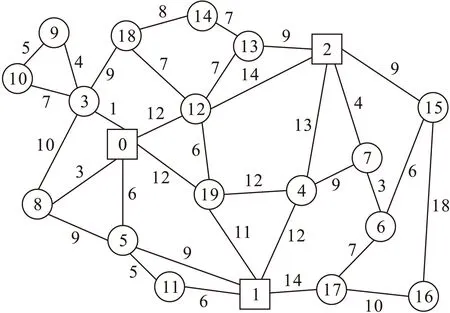
图2　逆向物流回收网络结构图Fig.2　Structure diagram of reverse logistics recovery network

改进的蚁群算法使用Matlab语言实现，运行环境为AMD Athlon(tm) 5200+2.70 GHz处理器，内存2 GB的Windows平台，通过大量的实验确定改进蚁群算法参数设置为α=1，β=5，γ=2，ρ=0.25，η=0.3，求得改进前后两种数学模型回收路径及运作费用如表3、4所示.

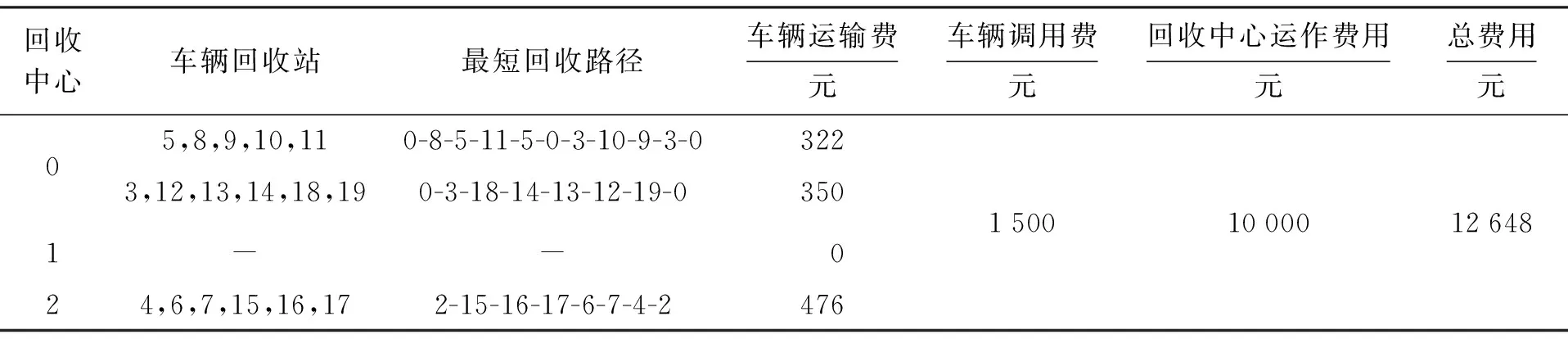
表3　改进后回收路径及运作费用Tab.2　Recovery path and operating expenses with improvement

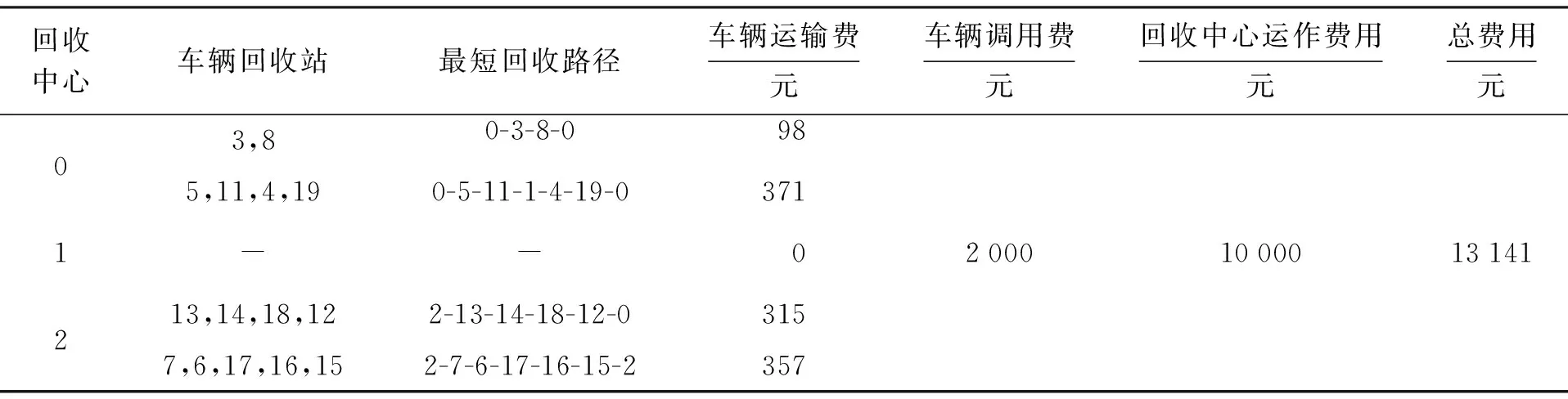
表4　改进前回收路径及费用Tab.4　Recovery path and operating expenses without improvement

通过表3与表4可直接得到逆向物流回收网络中的各个回收车辆的回收路径以及回收中心建设情况，计算结果给出了节点间存在不可行路径时回收车辆的最短行驶路径.本文所提出的数学模型中部分节点需要被多次访问，被多次访问的物流节点在第一次被访问时完成回收服务，实际逆向物流回收网络运作图如图3所示.对于传统VRP模型，当出现不可行路径时，放弃替代路径而搜索最短的可行路径进行回收任务，网络运作图如图4所示.

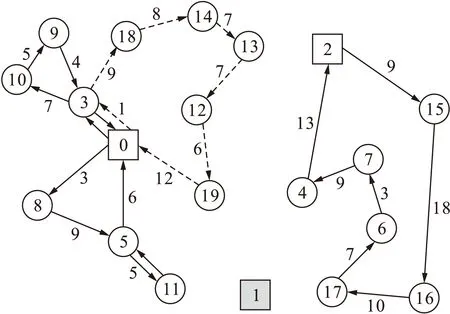
图3　实际物流网络运作图Fig.3　Actual logistics network operation diagram

由图3可以看出，为了满足所有回收站的回收需求，需要建立0、2两座回收中心，并发出3辆回收车辆；为了应对不可行路径产生的问题，出现部分非回收中心物流节点被多次访问的情况，如节点3与5.由图4可以看出，传统VRP问题不考虑物流节点可被多次访问情况，为了满足所有客户回收需求，则需要额外调用回收车辆去完成回收任务.特别对于节点9、10，两个节点仅与物流节点3相连，若节点3不可被二次访问，则节点9，10的回收需求无法满足.

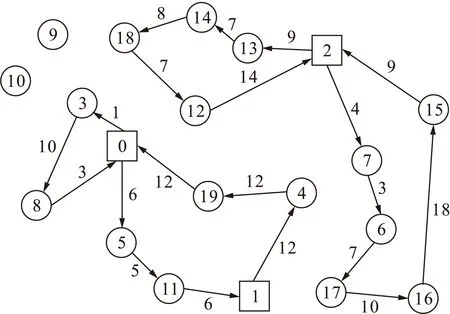
图4　传统VRP网络运作图Fig.4　Traditional VRP network operation diagram

通过上述计算结果分析可知，对于逆向物流回收路径问题的研究，考虑不可行路径与节点可被多次访问情况所建立的数学模型更加符合实际情况，具有很强的实际应用价值，很大程度节约了回收过程中的运输费用与回收车辆调用费用.

4　结　论

本文提出一种改进的蚁群算法求解一类不完全网络图下的VRP问题，当存在不可行路径时需要对部分节点进行二次访问来进行替代路径的搜索，因此，路径求解问题更为复杂.为了提高问题的求解效率，本文在传统蚁群算法基础上增加了距离矩阵更新操作.在实际应用中，可以将客户需求、回收站容量、物流网络可靠性等多方面因素加入模型进行讨论，使得逆向物流回收路径问题的研究能够更加贴近实际要求.

[1]高举红，赵天一.危险废弃物回收路径的优化分析 [J].中国安全科学学报，2013，23(11)：67-71.

(GAO Ju-hong，ZHAO Tian-yi.Analysis of routing optimization for hazardous waste recycling path [J].China Safety Science Journal，2013，23(11)：67-71.)

[2]蒋忠中，汪定伟.B2C电子商务中物流配送路径优化的模型与算法 [J].信息与控制，2005，34(2)：482-485.

(JIANG Zhong-zhong，WANG Ding-wei.Model and algorithm for logistics distribution routing of B2C E-commerce [J].Information and Control，2005，34(2)：482-485.)

[3]梁春艳，石宇强，张敏，等.基于 eM-Plant 的废旧家电逆向物流路径规划的仿真研究 [J].物流工程与管理，2014，36(3)：43-45.

(LIANG Chun-yan，SHI Yu-qiang，ZHANG Min，et al.Simulation of discarded appliances reverse logistics route planning based on eM-Plant [J].Logistics Engineering and Management，2014，36(3)：43-45.)

[4]Tolga B，Gilbert L.The pollution-routing problem [J].Transportation Research，2011，16(10)：1232-1250.

[5]Kim H，Yang J，Lee K D.Vehicle routing in reverse logistics for recycling end-of-life consumer electronic goods in South Korea [J].Transportation Research，2009，14(5)：291-299.

[6]Tang L，Galvao M.A tabu search algorithm for the vehicle routing problem with simultaneous pick-up and delivery service [J].Computer & Operation Research，2011，33：595-611.

(LI Hua-jun.Location-roution-inventor problem in optimization of reverse logistic system [D].Chengdu：Southwest Jiaotong University，2006.)

[8]任志刚.逆向物流网络选址优化策略研究 [M].北京：中国社会科学出版社，2011.

(REN Zhi-gang.Optimization strategy for facility location problem of reverse logistics center [M].Beijing：China Social Science Press，2011.)

[9]刘艳秋，焦妮，李佳.基于确定网络的多级物流网络优化设计 [J].沈阳工业大学学报，2015，37(1)：64-68.

(LIU Yan-qiu，JIAO Ni，LI Jia.Optimization design of multi level logistics network based on determined network [J].Journal of Shenyang University of Technology，2015，37(1)：64-68.)

[10]张德全，吴果林.最短路径问题的Floyd算法优化 [J].许昌学院学报，2009，28(2)：10-13.

(ZHANG De-quan，WU Guo-lin.Optimization of Floyd algorithm for shortest path problem [J].Journal of Xuchang University，2009，28(2)：10-13.)

[11]黄挚雄，张登科.蚁群算法及其改进形式综述 [J].计算技术与自动化，2006，25(3)：35-38.

(HUANG Zhi-xiong，ZHANG Deng-ke.Ant colony algorithm and summary of its improved algorithms [J].Computing Technology and Automation，2006，25(3)：35-38.)

(责任编辑：景勇英文审校：尹淑英)

Reverse logistics recovery path problem with considering unfeasible path

LIU Yan-qiu, WU Meng, XU Shi-da

(School of Science, Shenyang University of Technology, Shenyang 110870, China)

Aiming at the situation that the multiple accesses of some nodes have been seldom considered in the study on the problem of vehicle recovery path and in order to solve the problem that the feasible linear paths can not be entirely guaranteed in real life, a mathematical model with taking the minimum total transportation cost of reverse logistics network as the optimization objective was established. The problem is transformed into the traditional vehicle path problem model through the FLOYD algorithm, and is solved with the improved ant colony algorithm, the number and location of recycling facilities are determined, and the optimum vehicle recovery path is obtained. Furthermore, the validity of both model and algorithm is verified with a numerical example, which has certain practical significance for solving the problem of reverse logistics path.

reverse logistics; recovery path; unfeasible path; logistics node; recycling center; mathematical model; FLOYD algorithm; improved ant colony algorithm

2015-09-21.

辽宁省科学技术计划基金资助项目(2013216015)； 沈阳市科学技术计划基金资助项目(F13-051-2-00，F14-231-1-24).

刘艳秋(1963-)男，吉林四平人，教授，博士生导师，主要从事复杂系统可靠性建模与优化等方面的研究.

信息科学与工程

10.7688/j.issn.1000-1646.2016.04.10

TP 15

A

1000-1646(2016)04-0416-05

*本文已于2016-03-02 16∶47在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20160302.1647.042.html