三轴运动平台改进型交叉耦合轮廓控制*

王丽梅， 蔺威威

(沈阳工业大学 电气工程学院， 沈阳 110870)



三轴运动平台改进型交叉耦合轮廓控制*

王丽梅， 蔺威威

(沈阳工业大学 电气工程学院， 沈阳 110870)

为了削弱负载扰动及复杂轮廓误差模型对轮廓精度的影响，在单轴中采用比例控制作为位置环控制器，采用PDFF控制作为速度环控制器，以保证单轴跟踪精度.三轴间采用一种轮廓误差估算法来建立轮廓误差模型，运算更为简单.通过改进的交叉耦合控制结构进行轮廓控制器的设计，将轮廓误差的补偿量置于位置控制器前，能够实现跟踪误差与轮廓误差同时减小，以满足三轴运动平台的高精度加工要求.结果表明，改进后的三轴运动平台控制系统具有较高的轮廓精度和较强的抗扰性.

三轴运动平台； 永磁直线同步电机； 轮廓误差估算法； PDFF控制器； 交叉耦合控制； 跟踪响应； 跟踪误差； 轮廓精度

现代加工系统中，轮廓加工精度已成为重要的精度指标，其直接影响零件加工质量[1].直接驱动三轴运动平台是由轴向相互垂直运动的三台永磁同步直线电机(PMLSM)驱动而成，其加工零件运动过程中所产生的轮廓误差是由xyz三轴共同决定.

文献[9]建立了三维系统的空间轮廓误差模型，采用交叉耦合控制方式应用于三轴系统；文献[10]提出适用于多轴运动系统而且能被应用在非线性系统当中的等效误差法；文献[11]提出了具有模糊逻辑速度调节的前馈反馈控制器.上述所提出的控制方法虽然能够实现对三轴运动平台的轮廓控制，但这些方法的缺点是所建立的轮廓误差模型比较复杂，对控制器的设计造成很大困难，容易影响控制器的控制精度.

本文针对上述三轴运动平台数控加工系统控制方法存在的缺陷，采用一种轮廓误差模型估算法，与以往轮廓误差模型相比，此估算法更接近于真实模型，结构更简单、运算量更小.然后，将轮廓误差作为直接被控量，采用改进的三轴运动平台交叉耦合控制方法进行三轴间协调控制，达到数控加工平台系统的精度要求.

1　三轴运动平台系统模型

三轴运动平台采用由两两垂直的永磁同步直线电机进行轮廓精度试验，PMLSM机械方程式为

(1)

式中：Fe为电磁推力；Kf为电磁推力系数；M为PMLSM动子和动子所带负载的总质量；B为粘滞摩擦系数；v为电机动子速度；F为扰动力.

选取电机动子位置x(t)和电机动子速度v(t)为系统状态变量，即PMLSM状态方程可写为

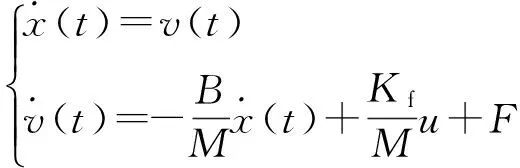
(2)

式中，u=iq，为电机的控制输入量.

直驱三轴运动平台系统模型可表示为

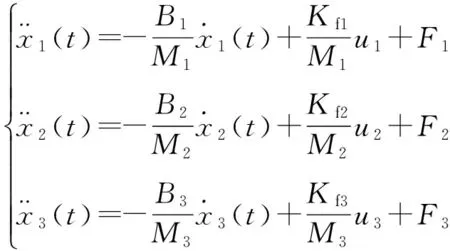
(3)

2　三轴运动平台轮廓误差模型及补偿

2.1轮廓误差模型建立

本研究以参数方程形式，采用一种更为简洁有效的轮廓误差演算法，可计算出三轴轮廓误差补偿量，并缩短运算时间，以确保控制精度良好.

图1为xyz空间上的直线轨迹跟踪，R为命令位置向量，P为实际位置，位置误差向量为E，轮廓误差为e.

图1　直线轮廓误差向量几何关系图Fig.1　Geometric relation graph of line contour error vector

由图1几何分析可知

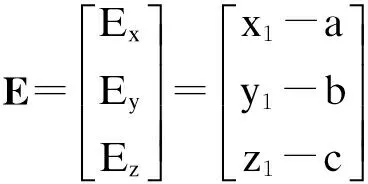
(4)

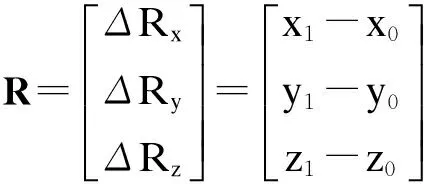
(5)

且根据R0、Q、R1三点可得命令位置线性方程式为

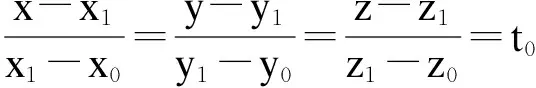
(6)

又因为Q点坐标为x，y，z，可得

(7)

可知向量dPQ与向量R相互垂直，即

dPQ·R=0

(8)

将式(5)和式(7)中的向量代入式(8)中可得

(9)

将式(9)求出的参数t0代回线性方程式(6)中，可得到与期望直线相垂直的坐标点Q，表示为

(10)

由图1可知，Q与P点坐标相减可得轮廓误差e，故轮廓误差可表示为

(11)

由式(11)可知轮廓误差e在x、y、z轴的分量.

2.2轮廓误差补偿

图2为轮廓误差补偿量几何关系图，由图2可知，若实际位置P能向命令位置修正，除了修正位置误差向量E在各轴分量Ex，Ey，Ez外，需另外补偿ex，ey，ez，整个补偿量C在各轴的分量可表示为

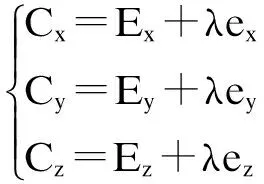
(12)

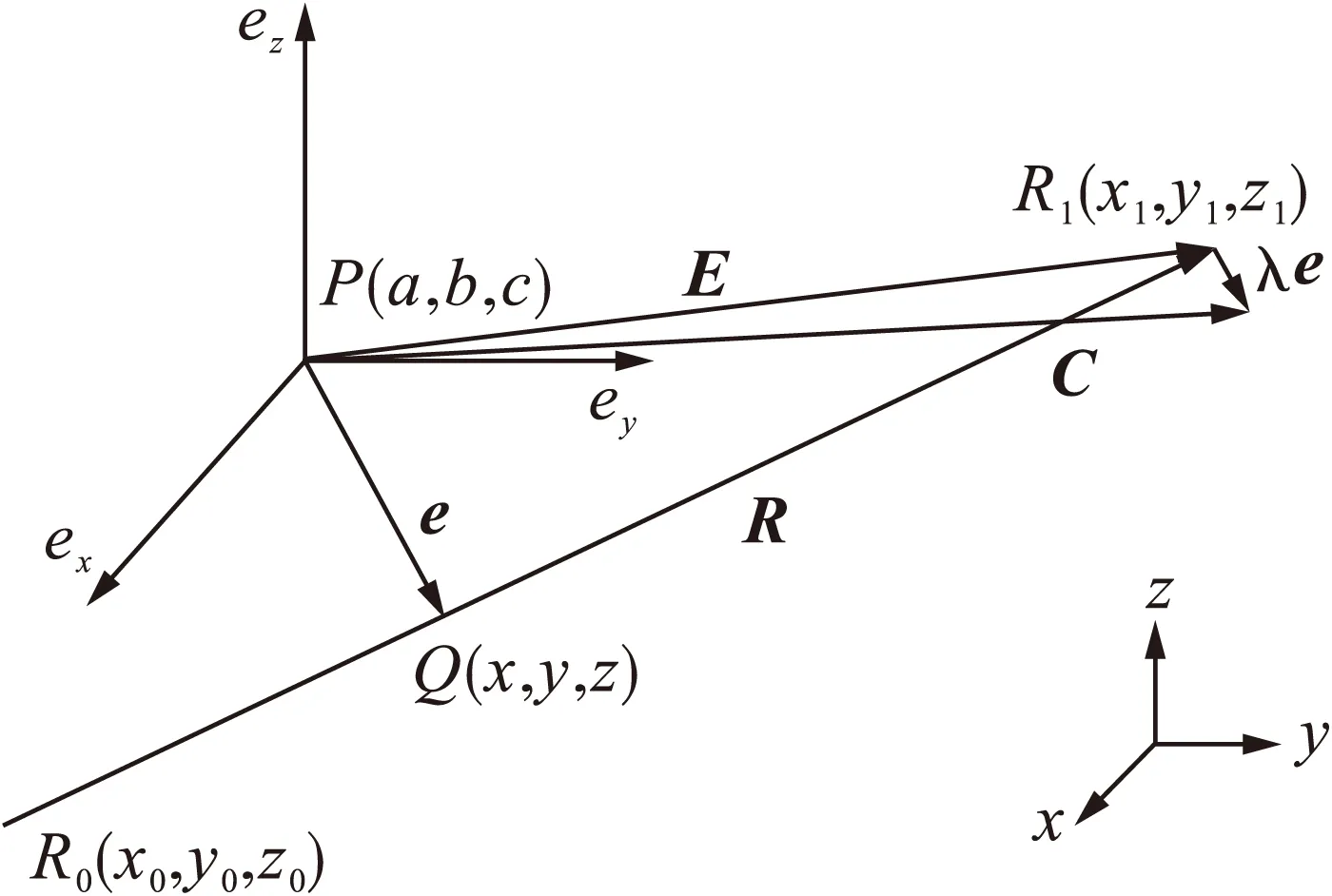
图2　轮廓误差补偿量几何关系图Fig.2　Geometric relation graph of contour error compensation

通过式(12)可使得合成向量C趋近于命令位置路径，其中λ为交叉耦合增益值，影响轮廓误差的修正速度.由合成向量C的几何关系可知λ值愈大，C愈偏向命令路径，修正轮廓误差e的量越大.

3　单轴位置控制器设计

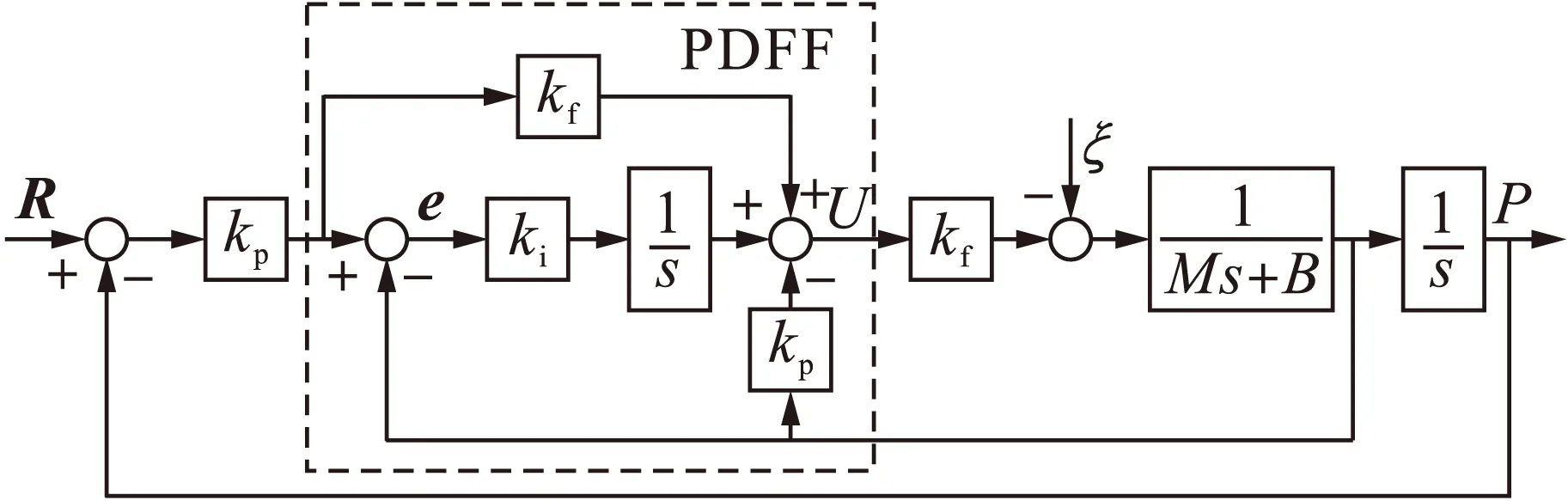
图3　单轴位置控制结构框图Fig.3　Structure block diagram of single axis position control

图3位置环中kp为比例控制器，速度环中采用的是PDFF控制器，其原理是在IP控制器的基础上加入一个前馈环节kf，在增加积分增益ki的情况下，也不会使系统产生超调.控制器的输入信号通过前馈环节kf可直接进入到系统中，使得系统的响应速度大大提高.

PDFF控制是PI控制以及IP控制两者中更为综合的控制方案，既弥补PI控制抗干扰能力较差的不足，又克服了IP控制响应速度较慢的缺点，在提高系统快速性的同时，还增强了系统的鲁棒性，加上位置环的比例控制更进一步保证了单轴的动态特性和稳定性.因此，单轴采用的这种控制方案对于高速高精度的数控加工平台能够有效地减小单轴的跟踪误差，提高单轴的位置跟踪精度及鲁棒性，间接地减小轮廓误差.

4　三轴改进型交叉耦合控制器设计

由前面采用的轮廓误差估算法可知，轮廓误差e仅与命令位置向量R和实际位置P有关，因此，所设计的交叉耦合控制器位于控制系统的回路部分，结构框图如图4所示.

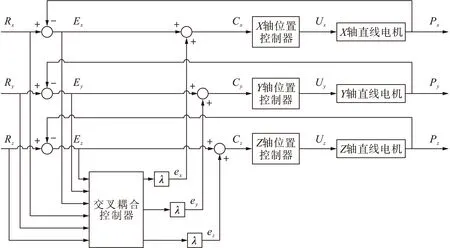
图4　三轴运动平台交叉耦合控制系统结构框图Fig.4　Structure block diagram of CCC system for three axis motion table

将本研究中所设计的三轴改进型交叉耦合控制器与传统交叉耦合结构相比较发现，本研究的轮廓误差补偿在位置回路控制器前就已完成.由图2轮廓误差补偿量几何关系可知，当调整控制器内的增益值kp时，会同时影响到轮廓误差补偿量C，其效果等同于调整C的大小，而非方向，但此时的方向是由因子λ的大小来决定，因此，kp与λ的调整是各自独立的，分别为轮廓误差的大小和方向.而传统交叉耦合结构则是将补偿量置于控制器后，当调整kp时，其效果等同于在图1中仅调整E的大小，所以本研究所采用的方法将轮廓误差补偿量C的方向和大小同时改变，在kp与λ间做最适当调整匹配.

5　仿真结果及分析

采用三台PMLSM作为三轴平台的驱动部件进行仿真研究，电机参数Mx、My、Mz为5.8、5.8、1.4 kg；Kfx、Kfy、Kfz为10.979 4、10.979 4、0.852 6 N/A；Bx、By、Bz为244.319 2 N·s/m；三轴位置控制器位置环比例系数Px、Py、Pz为210、210、195；PDFF控制器前馈补偿增益kfx、kfy、kfz为55.45、63.88、52.62；积分增益kix、kiy、kiz为4 500、5 500、4 000；比例增益kpx、kpy、kpz为38.22、58.34、45；三轴运动平台交叉耦合增益λ取0.1.由于系统期望输入是空间直线轨迹，其轨迹函数为x(t)=y(t)=z(t)=t0.

图5为三轴平台空间直线期望轨迹与实际输出曲线，可以明显看出，输出轨迹与期望轨迹基本重合.图6～8为x、y、z轴的跟踪误差曲线，跟踪误差均在10 μm范围内，说明本研究采用的单轴控制策略具有良好的跟踪精度.图9为三轴平台改进前后空间直线轨迹轮廓误差曲线；图10为10 s加入100 N扰动后，三轴平台的直线轨迹轮廓误差曲线.

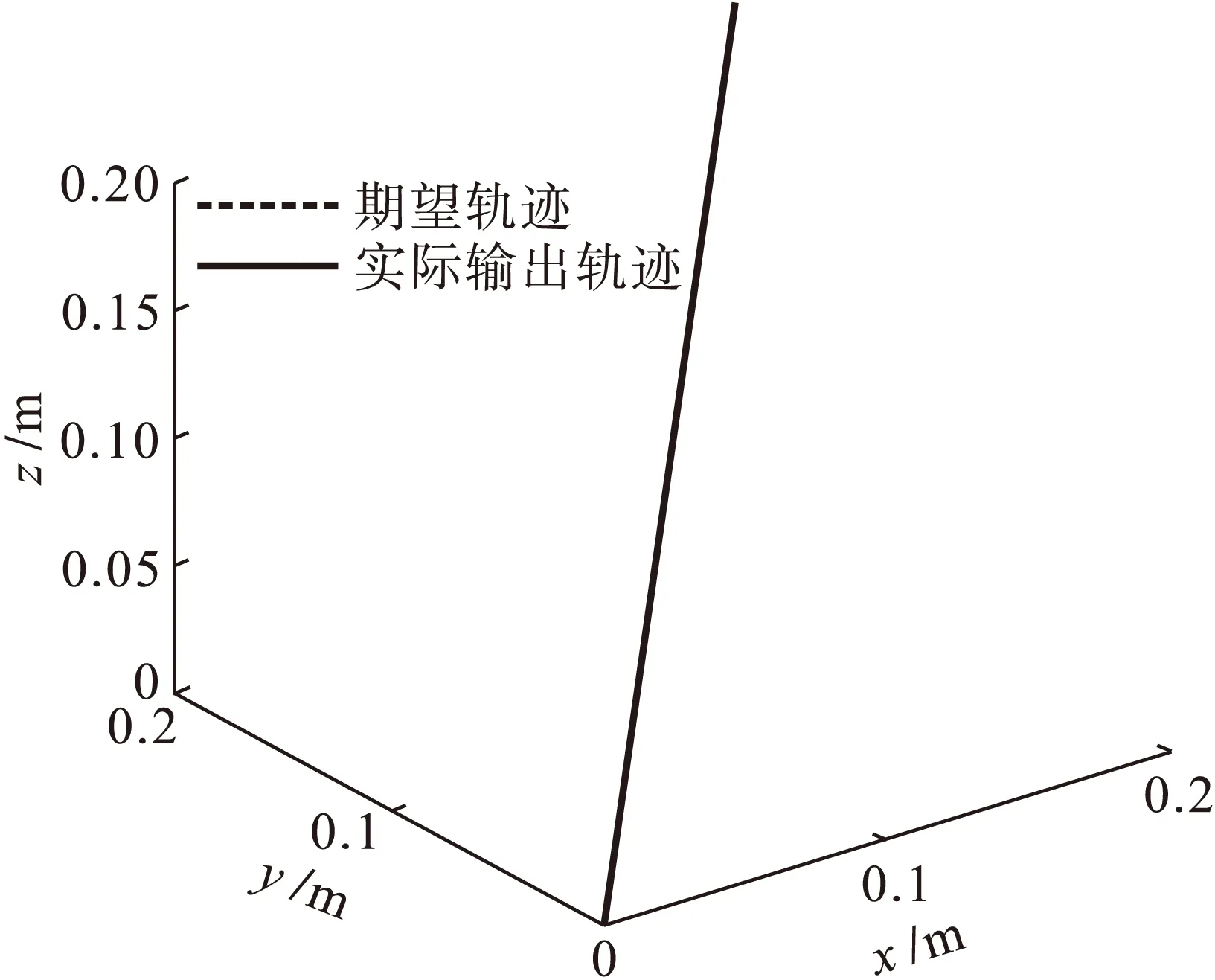
图5　期望轨迹与实际输出轨迹Fig.5　Expected and actual output trajectories

图6　x轴跟踪误差响应曲线Fig.6　Tracking error response curve of x axis

图11为同样仿真条件下，三轴运动平台空间螺旋线期望轨迹与实际输出曲线.三轴位置控制器位置环比例系数Px、Py、Pz为265、275、120；PDFF控制器前馈补偿增益kfx、kfy、kfz为38.25、40.23、45.11；积分增益kix、kiy、kiz为4 200、4 500、5 200；比例增益kpx、kpy、kpz为42.34、55.16、60.44；三轴平台交叉耦合控制增益λ取10；空间螺旋线各轴轨迹函数为x(t)=0.05sin 2πt，y(t)=0.05cos 2πt，z(t)=t0.

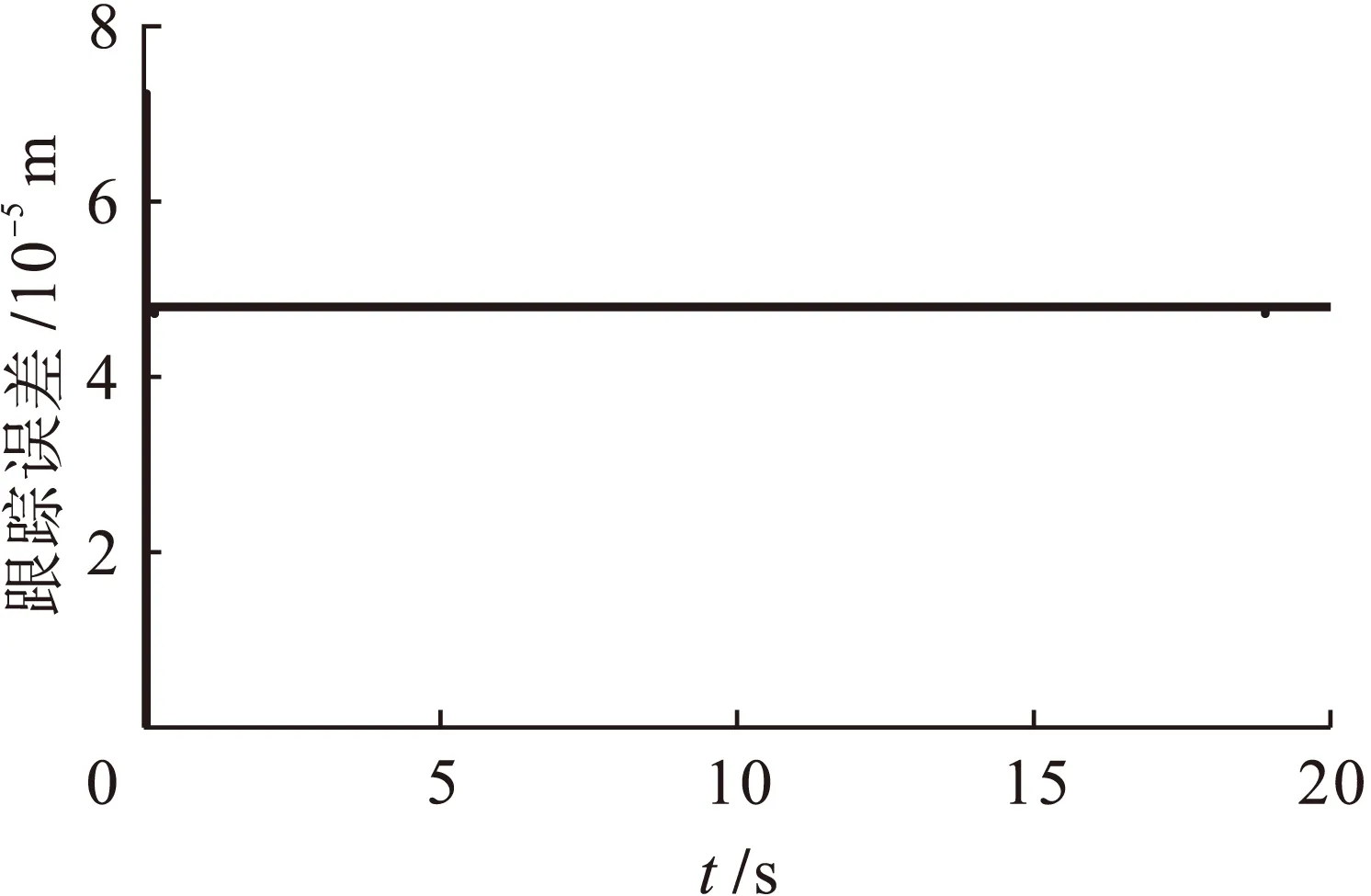
图7　y轴跟踪误差响应曲线Fig.7　Tracking error response curve of y axis

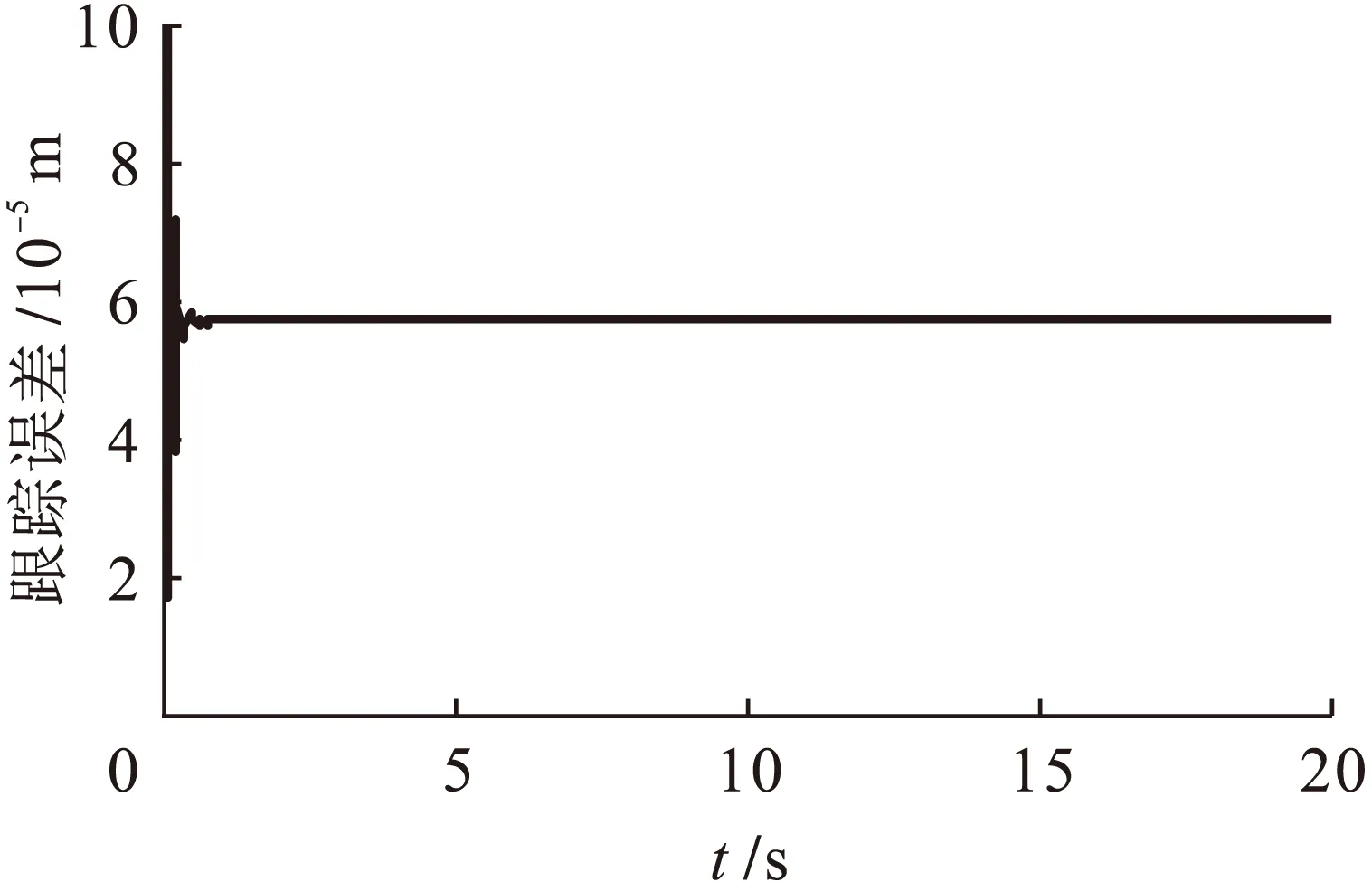
图8　z轴跟踪误差响应曲线Fig.8　Tracking error response curve of z axis

图9　改进前后空间直线轨迹轮廓误差Fig.9　Contour error of spatial line trajectory before and after improvement

图10　加入扰动后的空间直线轨迹轮廓误差Fig.10　Contour error of spatial line trajectory after adding disturbance

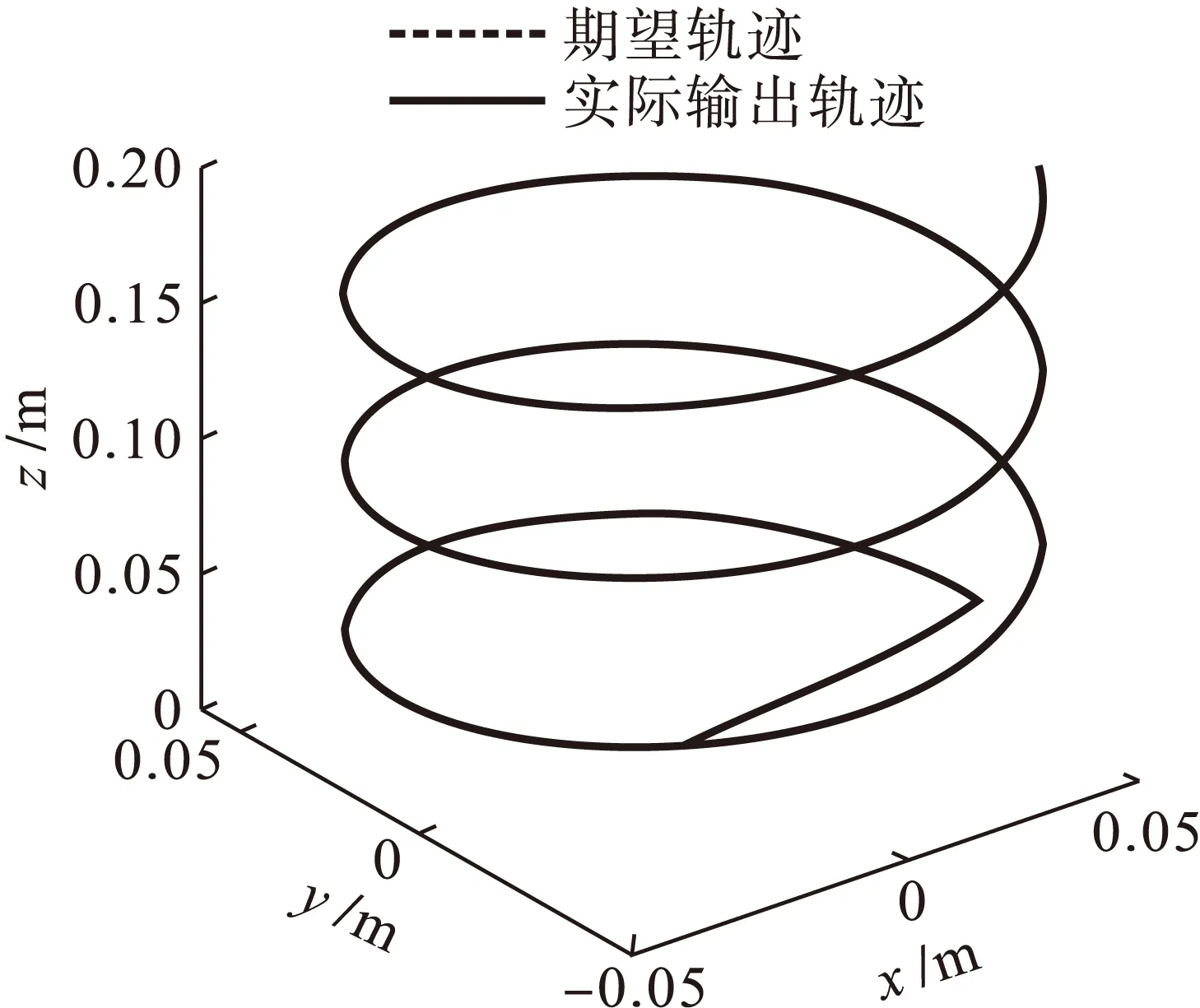
图11　期望轨迹和实际输出轨迹(螺旋线)Fig.11　Expected and actual output trajectories (spatial spiral line)

从图11中可以看出，采用轮廓误差估算法所设计出的改进型三轴交叉耦合控制器实际输出轨迹与期望轨迹基本相一致，说明该控制器具有良好的轮廓跟踪性能，能够满足轮廓跟踪控制的精度要求.图12～14为三轴平台的x、y、z轴跟踪误差曲线，可以看出各轴均有良好的位置跟踪精度.图15为三轴平台改进前后的轮廓误差曲线，改进后的交叉耦合控制器有效地减小系统轮廓误差，提高系统轮廓精度.图16为10 s时加入100 N扰动后，三轴平台的轮廓误差曲线，改进后的三轴交叉耦合控制器对三轴间协调控制有很强抗扰能力.

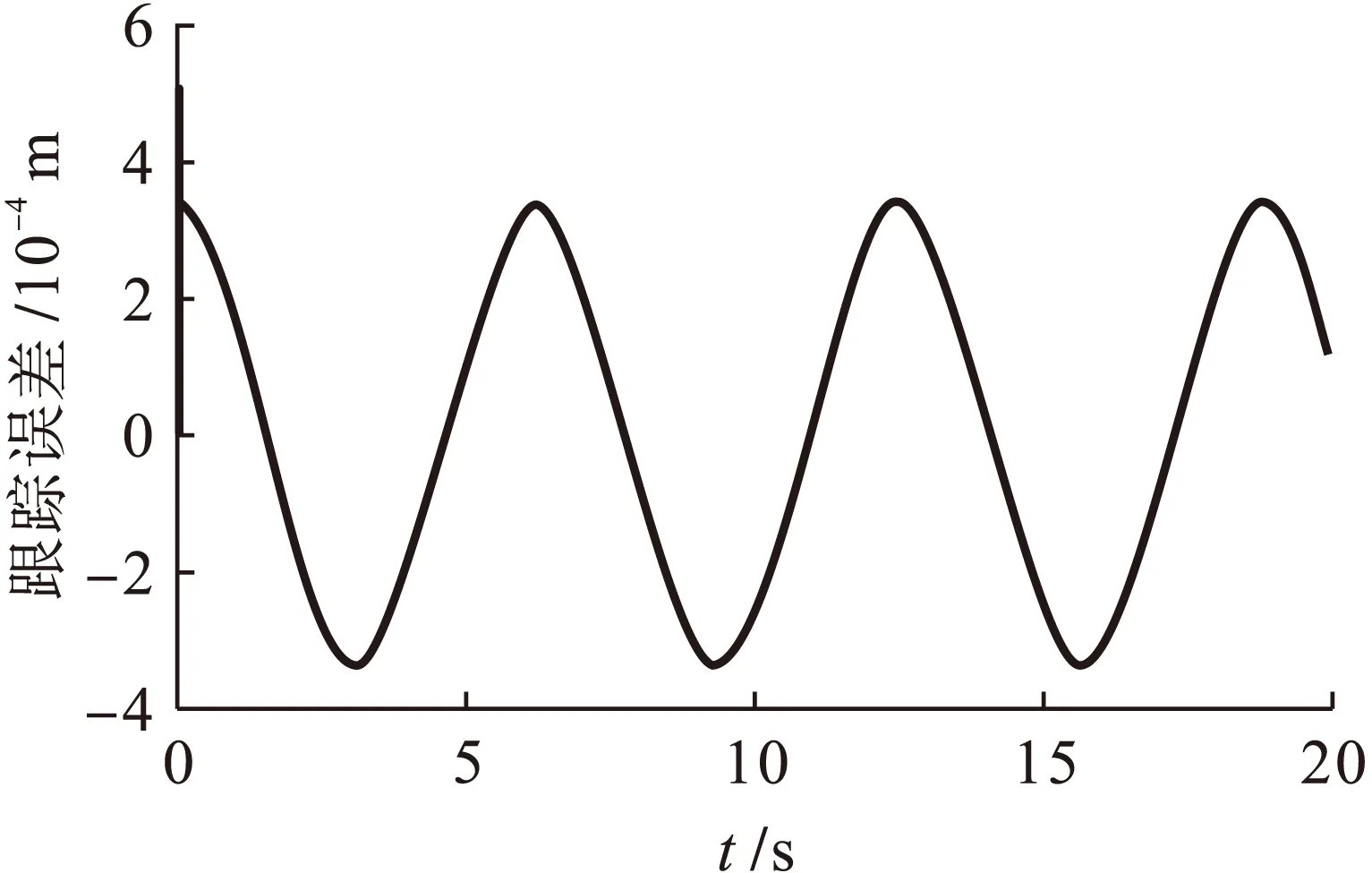
图12　x轴跟踪误差响应曲线(螺旋线)Fig.12　Tracking error response curve of x axis (spatial spiral line)

6　结　论

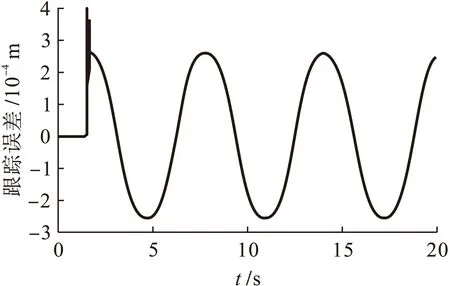
图13　y轴跟踪误差响应曲线(螺旋线)Fig.13　Tracking error response curve of y axis (spatial spiral line)

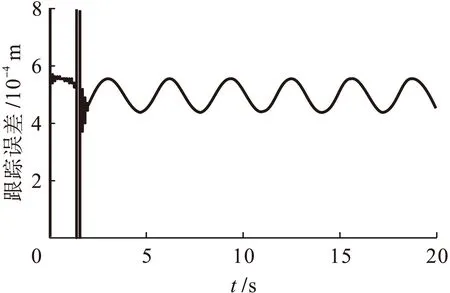
图14　z轴跟踪误差响应曲线(螺旋线)Fig.14　Tracking error response curve of z axis (spatial spiral line)

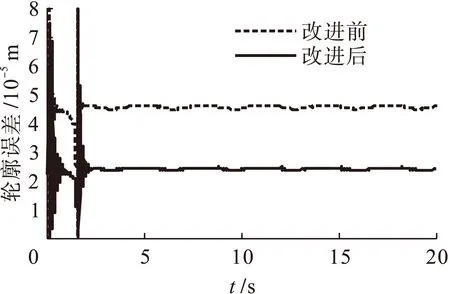
图15　改进前后空间螺旋线的轮廓误差Fig.15　Contour error of spatial spiral line before and after improvement

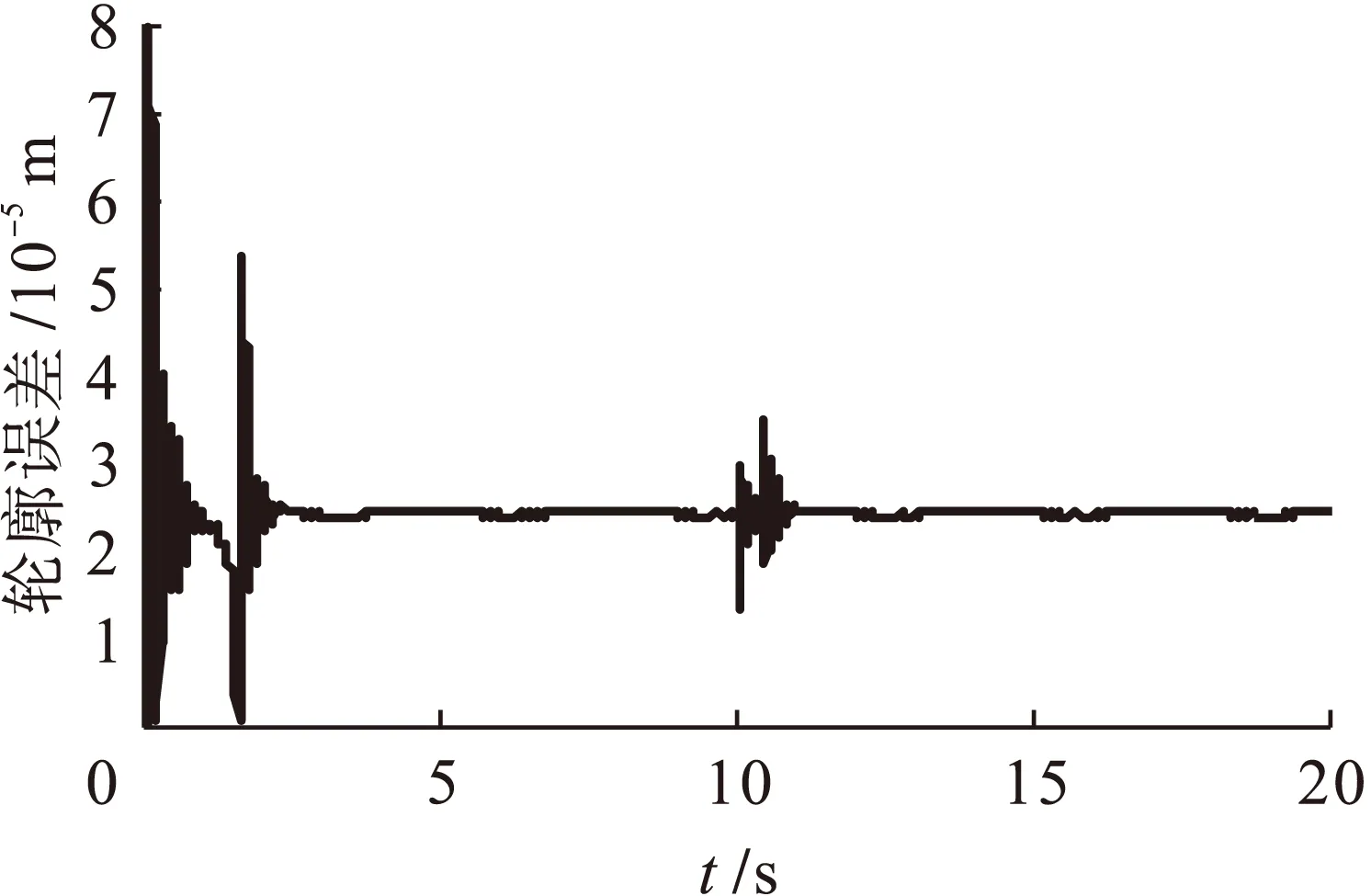
图16　加入扰动后空间螺旋线轮廓误差Fig.16　Contour error of spatial spiral line after adding disturbance

置跟踪精度.三轴间采用轮廓误差估算模型相比传统的轮廓误差估计算法更为简洁，运算量更小.根据该轮廓误差估计法设计的改进三轴交叉耦合控制器能够更好地进行三轴间的协调控制.仿真结果表明，所设计的控制系统有效地提高三轴运动平台的轮廓精度，增强三轴运动平台的抗扰动能力.

[1]赵希梅，郭庆鼎.基于ZPETC和CCC的直接驱动XY平台高精度控制 [J].组合机床与自动化加工技术，2011(2)：83-85.

(ZHAO Xi-mei，GUO Qing-ding.High precision control based on zero phase error tracking controller and cross-coupled controller for direct driveXYtable [J].Modular Machine Tool &Automatic Manufacturing Technique，2011(2)：83-85.)

[2]Ouyang P R，Pano V，Acob J.Contour tracking control for multi-DOF robotic manipulators [J].Journal of Pharmacy & Pharmacology，2013，33(2)：1491-1496.

[3]Kim K S，Zou Q.A modeling-free inversion-based iterative feedforward control for precision output tracking of lineartime-invariant systems [J].IEEE/ASME Transactions on Mechatronics，2013，18(6)：1767-1777.

[4]Rahaman M，Seethaler R，Yellowley I，et al.A new approach to contour error control in high speed machining [J].International Journal of Machine Tools & Manufacture，2015，88：42-50.

[5]王丽梅，左莹莹.基于RBF神经滑模的XY平台迭代交叉耦合控制 [J].沈阳工业大学学报，2014，36(1)：1-6.

(WANG Li-mei，ZUO Ying-ying.Iterative cross-coupled control forXYtable based on RBF neural sliding mode [J].Journal of Shenyang University of Technology，2014，36(1)：1-6.)

[6]Koren Y，Lo C C.Variable-gain cross-coupling controller for contouring [J].CIRP Annals，1991，40(1)：371-374.

[7]Yeh S S，Hsu P L.A new approach to biaxial cross-coupled control [C]//IEEE International Conference on Control Applications.Alaska，USA，2000：168-173.

[8]向雄海.交叉耦合适应性控制在数控工具机之研究 [D].高雄：国立高雄第一科技大学，2009：20-35.

(XIANG Xiong-hai.Cross-coupling adaptive control for CNC machine tools [D].Kaohsiung：National Kaohsiung First University of Science and Technology，2009：20-35.)

[9]Yeh S S，Hsu P L.Estimation of the contouring error vector for the cross-coupled control design [J].IEEE/ASME Transactions on Mechatronics，2002，7(1)：44-51.

[10]Chen S L，Wu K C.Contouring control of smooth paths for multiaxis motion systems based on equivalent errors [J].IEEE Transactions on Control Systems Technology，2007，15(6)：1151-1158.

[11]Cheng M Y，Su K H，Wang S F.Contour error reduction for free-form contour following tasks of biaxial motion control systems [J].Robotics and Computer-Integrated Manufacturing，2009，25(2)：323-333.

(责任编辑：景勇英文审校：尹淑英)

Improved cross-coupled contour control for three axis motion table

WANG Li-mei, LIN Wei-wei

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)

In order to weaken the influence of load disturbance and complicated contour error model on the contour accuracy, the proportional control was taken as the position loop controller and the PDFF control was taken as the speed loop controller in the single axis so as to ensure the tracking precision of single axis. A contour error estimation method was used to establish the contour error model among three axes, and thus the operation was simpler. The improved cross-coupled control (CCC) structure was adopted to design the contour controller, and the compensation amount of contour error was placed in the front of position controller. Therefore, the tracking error and contour error could be simultaneously decreased, and the highly precise machining requirements could be met for three axis motion table. The results show that the improved control system for three axis motion table has higher contour accuracy and stronger anti-disturbance ability.

three axis motion table; permanent magnet linear synchronous motor (PMLSM); contour error estimation method; PDFF controller; cross-coupled control (CCC); tracking response; tracking error; contour accuracy

2015-12-28.

辽宁省高等学校创新团队项目(201334068)； 辽宁省高等学校优秀人才支持计划项目(LR2013006).

王丽梅(1969-)，女，辽宁建平人，教授，博士生导师，主要从事交流伺服驱动技术等方面的研究.

电气工程

10.7688/j.issn.1000-1646.2016.04.01

TP 273

A

1000-1646(2016)04-0361-06

*本文已于2016-06-28 14∶25在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20160628.1425.002.html