基于“多站点”的城市常规公交线网优化设计

徐茜，俞礼军

（华南理工大学土木与交通学院，广东广州 510640）

基于“多站点”的城市常规公交线网优化设计

徐茜，俞礼军

（华南理工大学土木与交通学院，广东广州 510640）

针对目前城市常规公交线网设计中存在的问题，对公交线网进行优化设计，将交通小区对应到多个出发或到达站点即“多站点”，实现公交线网设计的“一次成网”，并将该思路的求解结果与单个站点进行了对比分析。

城市交通；公共交通；公交线网设计；交通小区；多站点

公共交通线网的设计是公共交通发展规划中的关键部分，如何规划城市公共交通网络，对于居民日常出行乃至城市经济社会健康发展有着举足轻重的影响。城市常规公交线网设计主要包括线网结构和线路频率的确定，以往的公交线网设计研究中多将交通小区对应到单个站点，与交通小区周边站点的实际设置情况不符。此外，已有的公交线网优化设计模型多存在忽略乘客换乘行为、求解结果不稳定、不同线路上站点重复率较高等问题。针对上述问题，该文提出将交通小区对应到多个出发或到达站点（简称“多站点”）的公交线网设计思路，并建立模型。该模型以系统总成本为目标函数，以线路长度、频率约束、运输能力等为约束条件，采用模拟退火算法求解。同时根据线路调整对初算解进行调整，以克服线路上站点重复率较高的问题。

1　公交线网设计模型的建立

1.1目标函数

乘客和运营者是公共交通系统中的两大主体，两者之间的利益相互冲突。高效的公交线网应既能满足乘客的出行需求，又不需运营者支付过高的运营成本，即需兼顾乘客和运营者双方的利益。因此，公交线网设计模型以系统总成本最小化为目标函数，系统总成本包含乘客出行成本和运营者成本两部分（见图1）。

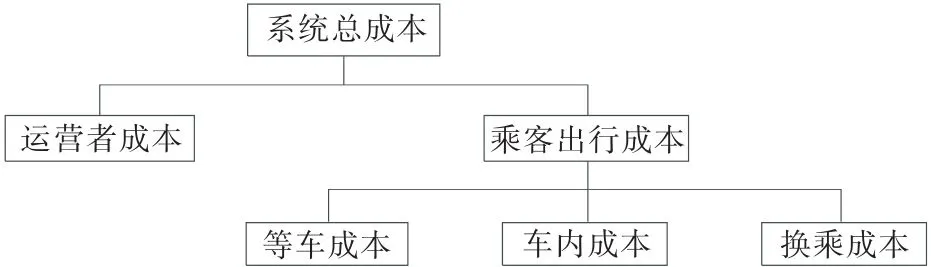
图1　公交线网总成本结构图

由图1可知，目标函数的表达式为：

TC=CU+CO

式中：CU为乘客出行成本，由等车成本CW、车内成本CI、换乘成本CR构成；CO为运营者成本。CU=CW+CR+CI

式中：N为路网中的节点总数；i、j为路网中的任意两个站点；rij为节点i、j间愿意换乘的乘客比例；qij为节点i、j间的需求量；T和TRWij分别为节点i、j间选择直达、换乘出行的乘客对应的平均等车时间（h）；VNRW和VRW分别为选择直达、换乘出行的乘客的单位等车时间价值（元/h）；TRij、VR、TIij和VI分别为乘客的平均换乘时间（h）、单位换乘时间价值（元/h）、平均车内时间（h）、单位车内时间价值（元/h）；fij、Dij分别为以节点i为起点、节点j为终点的线路对应的发车频率和线路长度；c为车辆的单位运营成本［元/（车·km）］。

1.2约束条件

（1）线路长度约束。公交线路长度应满足一定的约束条件。根据设计经验及实际情况，公交线路不宜过长，也不宜过短。根据算例路网的大小，假设研究线网中所有公交线路满足大于200m、小于3000 m的条件。对于以i为起点、j为终点的线路，有：

（2）频率约束。同一线路双向频率相等，线路发车频率需满足最大、最小发车频率的约束（算例中最大、最小发车频率分别取20、0），同时满足整数条件的限制，即：

（3）运输能力约束。以OD对的起点为考察对象，经过某一OD对的所有线路（包括直达线路、换乘线路）所能提供的服务应大于等于OD对间的乘客出行需求，即线路的运输能力至少应满足OD对间的出行需求。假设公交线网中所有运营公交车辆的车型及性能相同，且具有相同的车容量k。

式中：qij为OD对（i→j）间的乘客需求；fij为以i为起点、j为终点的线路Rij的发车频率；mij为辅助变量（0～1变量），若线路Rij为i→j间的直达线路或换乘线路（起点i至中间换乘点k间的线路），则mij=1，否则mij=0。

2　求解思路

线网设计问题的求解主要包括路网预处理、初始候选线路的生成、模型求解和线路调整。

2.1路网预处理

与已有研究不同的是，该设计将交通小区对应于多个站点，故在线网设计求解之前需对路网进行预处理，即通过增加虚拟节点描述交通小区内与路网产生联系的过程，并以此为依据对路网中的节点进行分类，确定各小区OD间的最短路径及对应的需求分配。

图2为路网的简单示意图，路网采用节点、路段、小区来描述。其中i表示中心节点，i1、i2、i3、i4表示小区i的分配节点，1、2、3、4表示小区i内的交叉节点（即公交站点），路段是指图中所示所有节点间的连线。

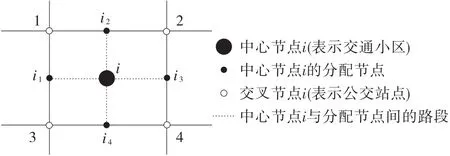
图2　路网中节点、路段、小区示意图

2.2初始候选线路的生成

最短路径的求解算法较多，包括Floyd算法、Dijkstra算法、K最短路算法等。这里采用Dijkstra算法求解各节点间的候选线路，并根据线路长度约束对生成的最短路径进行筛选，确定初始候选线路集合。被剔除的线路令其发车频率为零。

2.3模型求解

采用模拟退火算法对建立的公交线网设计模型进行求解。主要步骤为：

（1）确定初始温度T、初始解S及每个温度下的最大迭代次数L，令k=1。

（2）根据上一次迭代计算的解与随机数η确定此次迭代的新解Sk。

（3）fSk（ ）为当前解对应的评价函数，即设计模型中的目标函数。判断fSk（）与fS（）的大小，若fSk（）＜fS（），则接受当前解，令S=Sk，即将当前解存储为最优解；否则，以概率θ=exp［（f（Sk）-f（S））/T］接受当前解。

（4）若满足迭代终止条件，则算法结束；反之，令T=T/k，返回步骤2，继续下一温度下的解的搜索过程。

2.4线路调整

根据已提出的线路合并与取消思路，对生成的线网解进行调整，以避免线网解中不同线路间的站点重复率高的问题。

2.4.1线路取消

若线路Ri′j′包含于线路Rij，即线路Ri′j′上的所有站点均在线路Rij上，则2条线路中只保留线路Rij，取消线路Ri′j′，令fi′j′=0。

2.4.2线路合并

若线路Ri′j′从起点站开始，30%的站点为线路Rij上的连续站点，且最多通过两路段可实现Rij与Ri′j′两线路终点站间的连接，则取消线路Ri′j′，令fi′j′=0。

3　算例及结果分析

以7个交通小区、15个节点（交叉节点）、44条路段（双向）构成的简单路网为例（见图3），对单一模式下基于“整体规划”的城市常规公交线网设计问题进行研究。为便于研究，对原路网进行预处理，结果见图4。处理后的路网由7个交通小区、15个节点（交叉节点）、82条路段（双向41条路段）构成。

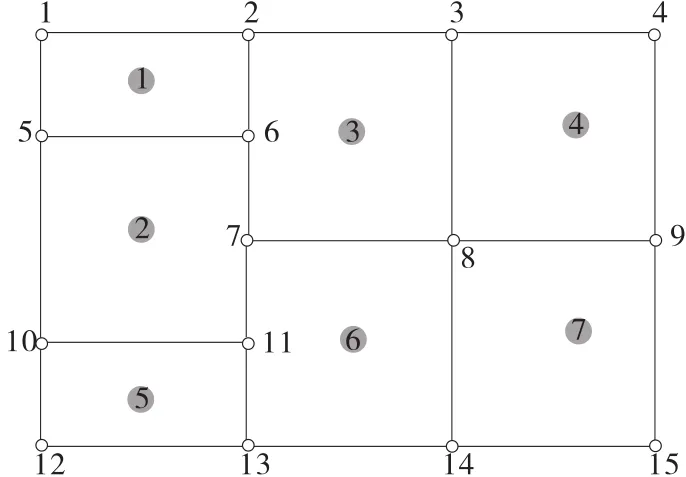
图3　算例路网示意图

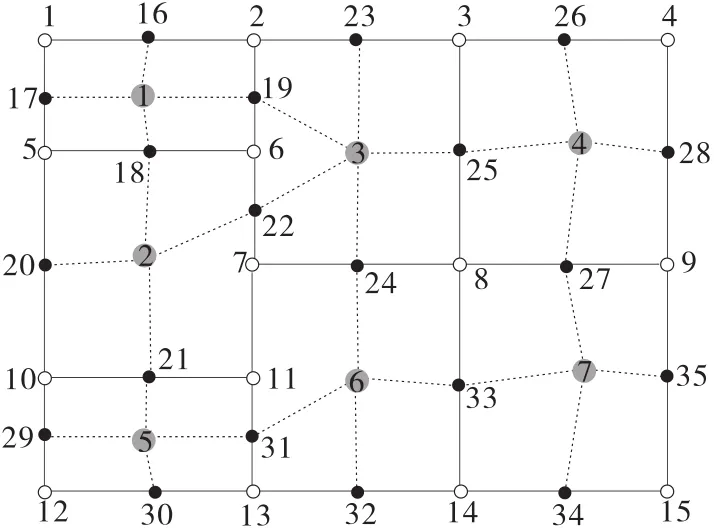
图4　处理后的路网示意图

假设公交车的行驶速率均为30km/h；愿意通过换乘到达目的地的乘客比例为0.05；乘客车内时间价值为30元/（人·h），不愿换乘的乘客车外时间价值为50元/（人·h），愿意换乘乘客的车外时间价值为70元/（人·h）；车辆容量为70人/车；每次停靠站时间为0.02h。客车运行成本主要包括燃油消耗、通行费、人员工资等，加上车胎耗损费、人员费用、企业运转办公费用等，折合的单位运营总成本为30元/（车·km）。其他已知条件见表1～4。

根据上述已知数据，对算例路网进行求解，结果见表5。由表5可知：求得的最优解中系统总成本为13910元，线路总数量为5条（双向10条）。为对该思路下的求解稳定性进行研究，进行多次试算。试算结果表明该思路下的求解结果较稳定。

表1　OD需求矩阵　人

表2　交通小区相关数据

表3　分配节点对应的交通小区归属情况

表4　交叉节点及分配节点的坐标

表5　算例路网的求解结果

4　结语

该文将交通小区对应于多个站点，对城市常规公交线网设计问题进行研究，更符合交通小区周边站点的实际设置情况。研究中考虑了乘客的换乘行为，建立了以系统总成本为目标函数，以线路长度、频率等为约束条件的公交线网设计模型。对该模型采用模拟退火算法求解，并应用线路调整思想对线网解进行调整，有效克服了不同线路上站点重复率高的问题，且通过多次试算，该思路下的模型求解结果较稳定。

［1］ 俞礼军，梁明苹.基于整数非线性规划的城市常规公交线网优化设计［J］.中国公路学报，2016，29（2）.

［2］ 梁明苹.公交线网设计算法分析及线路调整研究［J］.公路与汽运，2015（7）.

［3］ 高伟.城市轨道交通关联常规公交接驳线网优化研究［D］.长沙：中南大学，2012.

U491.2

A

1671-2668（2016）04-0032-04

2016-03-20