考虑疲劳寿命的负载隔离式电动汽车车架轻量化研究∗
2016-09-14周美施尹怀仙张铁柱张洪信刘高君
周美施,尹怀仙,张铁柱,张洪信,刘高君
(青岛大学机电工程学院,山东青岛 266071)
考虑疲劳寿命的负载隔离式电动汽车车架轻量化研究∗
周美施,尹怀仙,张铁柱,张洪信,刘高君
(青岛大学机电工程学院,山东青岛 266071)
对某改装负载隔离式电动汽车车架的静强度、疲劳强度进行验证并进行轻量化研究。首先利用Solidworks对车架进行参数化建模,导入ANSYSWorkbench中计算车架受力,利用SN法分析得到车架疲劳寿命,然后以此为约束建立车架优化设计模型,对车架各梁结构的壁厚进行优化设计,使车架质量减轻29.09%。
汽车;电动汽车;负载隔离;疲劳寿命;车架;轻量化
汽车零部件通常因为结构振动而发生疲劳破坏,提升汽车零部件疲劳强度、可靠性及安全性具有极其重要的意义。现今汽车零部件疲劳强度的提高主要凭借经验设计,通过静态优化方法等实现。学者们从不同方面对结构寿命优化问题作出了分析研究:HaibaM.等通过多体动力学分析软件确定疲劳载荷谱,实现车辆悬架系统关键部件的疲劳寿命优化;杜中哲利用时域疲劳分析仿真计算某SUV轿车车身结构的疲劳寿命分布,并利用频域疲劳寿命分析方法对时域方法的精度进行了论证;薛彩军等建立基于响应面模型的结构疲劳寿命优化方法,对飞机起落架进行了疲劳优化设计;吴道俊等提出了基于疲劳寿命的车架支架拓扑优化流程;何卫锋等运用优化设计分析方法建立了某机翼的数学模型,其优化目标为机翼结构疲劳寿命和结构质量;归晓烨等以某型运输机前起落架为研究对象,利用MSC工程软件,建立了基于疲劳寿命的多体结构优化方法;贺新峰等以搅拌车副车架为研究对象,提出了将等效静载荷结构优化方法、拓扑优化方法与疲劳预测相结合的疲劳设计方法。目前对汽车零部件的疲劳寿命分析已有一定方法,如E-N法、S-N法和振动疲劳分析法等,但将汽车零部件的疲劳寿命为优化目标的结构优化设计研究还不多,如何考虑疲劳寿命设计合理的材料分布、结构形式及其尺寸,实现车架轻量化、降低成本和提高行驶里程已成为亟待解决的热点问题。
1 负载隔离式电动汽车结构原理
负载隔离式电动汽车是一种新型纯电驱动汽车,发动机和发电机仅作为能量转换装置,发动机始终工作在最佳稳态工况点,不受车辆负荷变化的影响。如图1所示,控制器控制两组储能电池组进行合理的充放电切换:储能电池组1首先放电并提供动力,当其电量达到报警电量时,控制器控制储能电池组2开始放电,在提供动力的同时,发电机组开启给电池组1充电。这样两组储能电池组循环进行充放电,使电池组避免出现过充、过放和过热危险,大大增加电池组的使用寿命,同时根据油箱大小增加汽车的续驶里程。
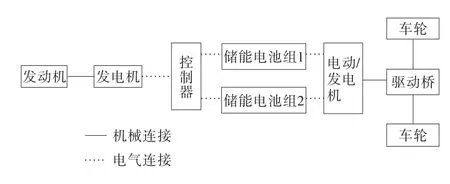
图1 负载隔离式电动汽车的工作原理示意图
车架自重通过设置材料密度参数、重力加速度添加,车架各部分总成简化为集中力添加在车架相应部位。计算所需载荷和加载方式见表1。
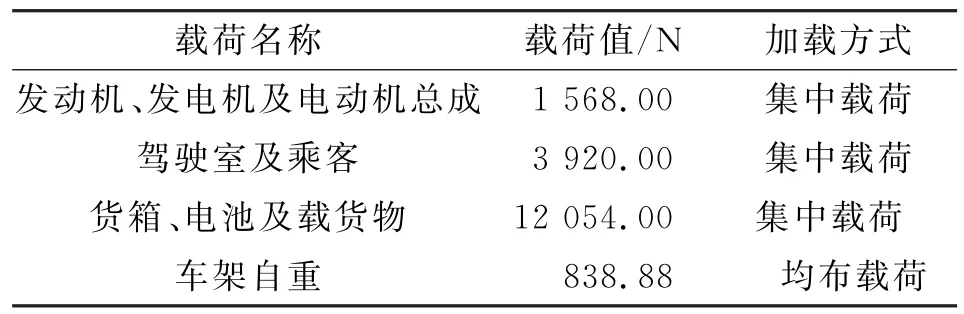
表1 车架各载荷及添加方式
2 车架疲劳寿命分析
在车架建模过程中,为方便网格划分,去除倒角、引线安装等的小圆孔及对承重不受影响的安装结构件。同时,由于需进行结构参数优化,对该车建立参数化模型。建模方法有两种:一种是先在三维软件中建立参数化模型,再导入Workbench中;另一种方法是在Workbench中直接建立模型,并设定参数。这里选用第一种方法建立模型,针对车辆行驶最恶劣工况,即悬空工况进行强度计算及疲劳寿命分析。
金属在循环载荷作用下会发生疲劳破坏。车架疲劳寿命分析必须以车架有限元分析结果为依据。因该文主要研究车架静态疲劳特性,需获得车架的静力学分析结果。静态分析主要是通过对车架施加静态载荷和约束,获得车架变形、应力分布情况。针对电动汽车悬空工况进行分析,载荷施加见表1。选用第四强度理论校核车架的静强度,即:
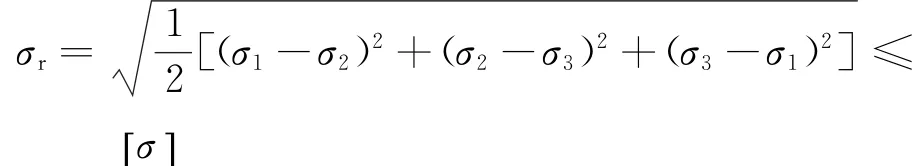
式中:σr为相当应力;σ1、σ2和σ3分别为3个方向的主应力;[σ]为材料的许用应力。
通过有限元计算,得到车架应力和位移(见图2和图3)。车架悬空工况下的最大应力值σmax=135 MPa<[σs],出现在后悬架吊耳处。车架的安全系数约为2.6,大于一般经验安全系数,满足强度要求,其最大位移δmax=1.69mm,满足刚度要求。
图2 车架应力云图(单位:Pa)
载荷谱在疲劳分析中极为重要,决定疲劳分析结果的准确度。疲劳分析中的载荷谱分为时间序列载荷谱和时间步载荷谱、恒定幅值载荷谱等,该文对车架进行静态疲劳分析,采用时间序列载荷谱。要获取车架较为准确的疲劳分析结果,需通过试验获取载荷谱,但由于条件有限,通过ADAMS整车虚拟样机仿真提取动态力的方式得到车架各荷载的动态力。经过分析,得到该车在30s内以50km/h在C级路面行驶时出现峰值力的次数为9次。将载荷谱采用峰谷值法进行简化,得到车架时间载荷序列(见图4)。
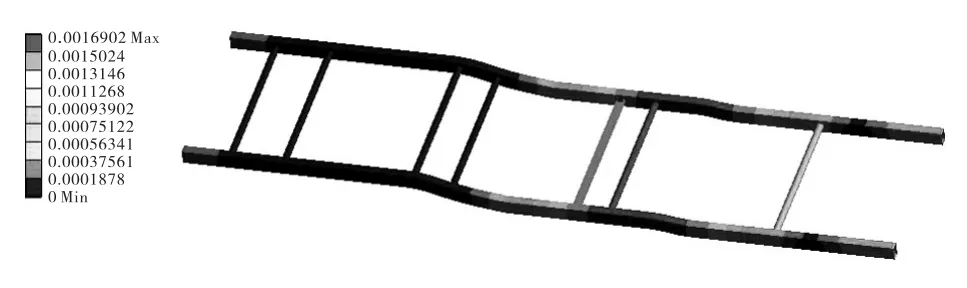
图3 车架位移云图(单位:m)
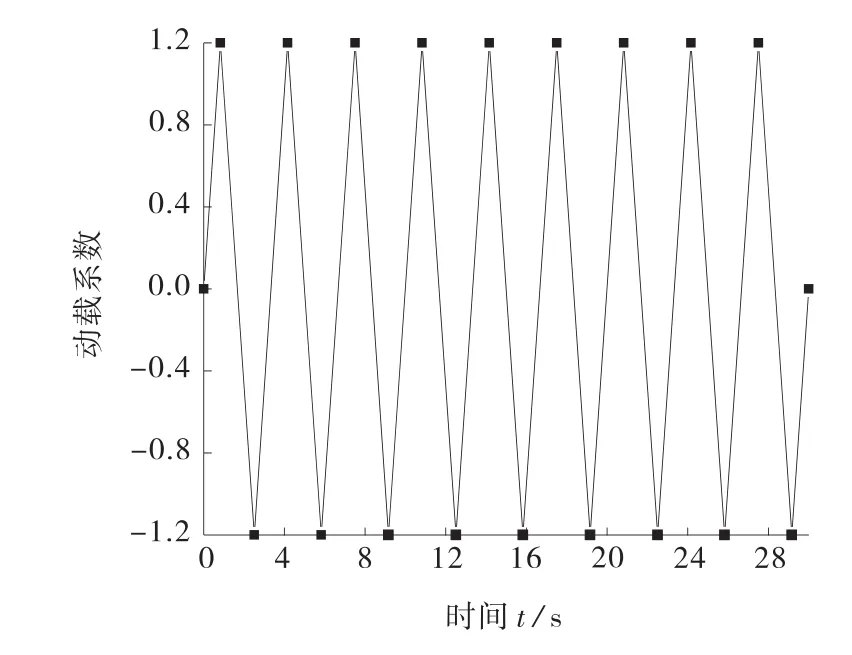
图4 车架时间载荷序列
ANSYSWorkbench中有丰富的材料数据库,从中查取Q345所对应的材料StructuralSteel BS4360Grade50D,获得应力比为-1,Q345的S-N曲线见图5。由于获得的材料为美国标准,加上材料表面粗糙度、应力集中等的影响,需对材料S-N曲线进行修正。采用S-N法,使用Goodman曲线修正,结合有限元分析结果进行疲劳分析得到的车架疲劳寿命见图6。
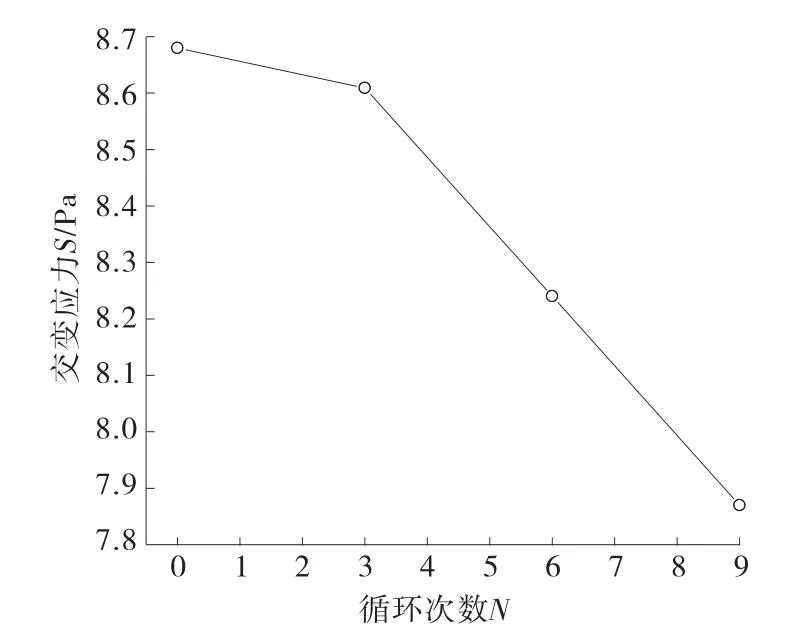
图5 Q345的S-N曲线
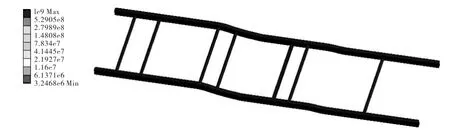
图6 车架疲劳寿命云图(单位:次)
由图6可见:该车架的疲劳寿命为3246800次,最危险点出现在后悬空车轮纵梁与悬架连接位置。根据《机动车强制报废标准规定》,该车行驶里程参考值为500000km。根据载荷谱计算得到其车架许用疲劳寿命为1000000次,车架满足疲劳寿命要求。
3 基于疲劳寿命的车架轻量化
根据车架静强度和疲劳寿命计算结果,该车架强度及疲劳寿命存在较大冗余。而汽车质量与油耗直接相关,汽车质量下降10%,油耗降低6%~8%。因此,对该车架进行轻量化设计。
目前,基于疲劳寿命的结构件尺寸优化有两种基本思路:一种是将设计寿命作为约束,在使寿命达到设计要求的前提下,将结构件质量最轻设置为目标函数;另一种是将结构总质量作为约束,在满足结构总质量的要求下,将结构疲劳寿命最大作为目标函数。这里按照第一种基本思路进行优化,在满足约束的条件下,运用优化算法,通过迭代反复计算,求得目标函数的极值,从而得到最优尺寸参数。尺寸优化模型为:
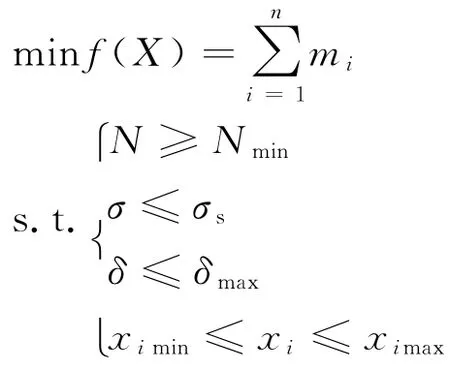
式中:mi为第i个单元的质量(kg);Nmin为车架的许用疲劳寿命(次);σs为车架的屈服强度(MPa);δmax为车架结构要求最大位移(mm);xi为第i根梁的厚度(mm);ximin、ximax分别为第i根梁的厚度下限和上限(mm)。
车架各部件的设计变量见图7。
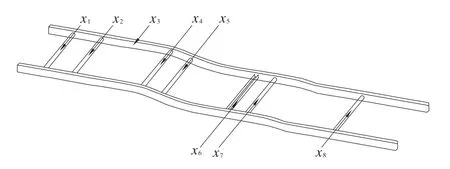
图7 车架各部件的设计变量
设计变量取定后,还需确定优化设计中的性能约束。有限元计算分析中,状态变量可以是结构的材料属性、固有频率和位移值等,其合理取值范围对结构优化设计具有重要影响。在此确定优化设计数学模型状态变量为:1)强度状态变量,要求结构的安全系数不超过2,结构许用疲劳寿命大于Nmin=1000000次循环。2)静刚度状态变量,要求车架结构的最大位移量不超过δmax。优化结果见表2。
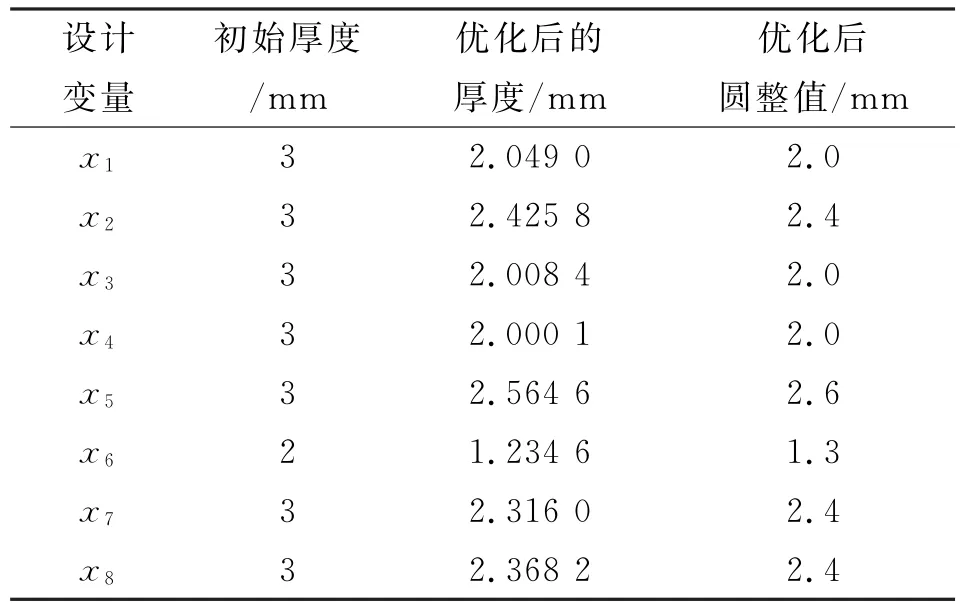
表2 结构部件优化前后的厚度
对结构改进后车架进行疲劳寿命分析,在极限工况下其安全系数为2.3,且有一定余量,最大位移值为2.27mm,疲劳寿命为1.1369×106次。优化后车架质量由85.6kg减少至60.272kg,降幅达29.09%,实现了轻量化目标。
[1] 涂善东,赵永翔.机械强度学科发展趋势[J].机械强度,2005,27(4).
[2] HaibaM,BartonDC,BrooksPC,etal.Thedevelopmentofanoptimizationalgorithmbasedonfatiguelife [J].InternationalJournalofFatigue,2003,25(4).
[3] 杜中哲.轿车车身结构及焊点的疲劳寿命分析与优化改进研究[D].上海:上海交通大学,2006.
[4] 薛彩军,谭伟,徐奋进,等.基于响应面模型的结构疲劳寿命优化方法[J].南京理工大学学报:自然科学版,2011,35(6).
[5] 吴道俊,钱立军,祝安定,等.基于疲劳寿命的车架支架结构优化[J].汽车工程,2013,35(10).
[6] 何卫锋,吴显吉,何宇廷,等.某机翼结构细节抗疲劳优化设计[J].机械强度,2003,25(3).
[7] 归晓烨.基于疲劳寿命的多体结构优化方法研究[J].科学技术与工程,2012,12(33).
[8] 贺新峰,于德介.基于ESLs结构优化法的搅拌车副车架疲劳设计[J].振动与冲击,2013,32(14).
[9] 张洪伟,张以都,王锡平,等.基于ANSYS参数化建模的农用车底盘优化设计[J].农业机械学报,2007,38 (3).
[10] 刘鸿文.材料力学[M].北京:高等教育出版社,2010. [11] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.
[12] 宋年秀,刘祥斌,曲秀丽.基于MSC.Patran的牵引车车架轻量化设计[J].公路与汽运,2013(2).
[13] 邓仲卿,阳林,李琦,等.城市电动客车车身结构拓扑优化设计[J].客车技术与研究,2013(2).
[14] GB00855-2012,机动车强制报废标准规定[S].
[15] 周美施,尹怀仙,张铁柱,等.电动客车车架等寿命轻量化研究综述[J].农业装备与车辆工程,2016,54 (2).
U469.72
A
1671-2668(2016)04-0001-03
∗国家高技术研究计划项目(2014AA052303);山东省科技发展计划项目(2014ZZCX05501;2014GGX103044);青岛市战略性新兴产业培育计划项目(14-8-1-2-gx)
2016-02-25
