基于引力模型的重庆市对外交通发展实证分析

2016-09-14王晶1汪欢2

公路与汽运 2016年4期

关键词：城市交通引力重庆市

王晶1，汪欢2

（1.重庆市交通规划研究院，重庆 400020；2.合肥师范学院电子信息工程学院，安徽合肥 230601）

基于引力模型的重庆市对外交通发展实证分析

王晶1，汪欢2

（1.重庆市交通规划研究院，重庆 400020；2.合肥师范学院电子信息工程学院，安徽合肥 230601）

传统的交通吸引仅限于微观交通，对于地区性的宏观交通不能很好地把握。物理学中的引力模型可以将区域交通进行模块化分界。文中以重庆市为例，利用断裂点理论计算重庆市到周边4座同级相邻城市（成都、西安、长沙、贵阳）的断裂点位置，然后连接各断裂点，确定重庆市的交通吸引范围；根据城市吸引范围的形状走势，分析重庆市对外交通空间发展趋势，指出重庆市对外交通的发展方向，为相关部门提供战略决策建议。

城市交通；对外交通；引力模型；交界区域；重庆市

交通出行可视为刚性需求，但随着交通方式的丰富、交通区域的扩大，交通中心站点的选择越来越多。一定程度上，区域交通服务辐射范围的交叉使模块化服务的交通网络出现交通吸引，这一点与城市化吸引类似。引力模型是早期用来分析空间作用的经典力学模型，现已被广泛应用到各类学科领域，其中比较成熟的有城市规划领域与国际贸易学说。城市引力模型早期被应用于城市间的空间作用与市场经济研究，后来也被广泛用于研究区域经济联系、城市间相互作用结构及城市间贸易、物流联系等研究。该文在上述城市引力模型研究的基础上，提出地区交通引力模型，即将交通枢纽城市作为空间引力点，通过公路里程、经济水平、人口数量等指标权重改造引力模型，确定交通枢纽城市的交通吸引范围，并对重庆市对外交通发展进行实证研究。

1　交通引力模型

令城市间的交通引力表示区域交通联系量或交通空间相互覆盖作用量的大小，综合反映城市对外交通服务覆盖能力。区域交通联系量有相对联系量与绝对联系量之分，前者表示对象城市被其他交通枢纽城市引力辐射的程度，后者反映交通枢纽城市对周边小城市的交通引力覆盖程度。当一定片区内存在两个交通影响力相近的区域性交通枢纽时，两者之间会存在相互吸引及对周边小城市辐射覆盖重合的现象，这一点类似于寡头博弈。

交通引力大小与城市综合实力水平及枢纽地段密切相关，表现为实力大的城市交通吸引力大，即出行聚集现象，表明大城市对小城市的交通辐射程度越大，两者间的相对交通联系量也越大；而对于处于引力重合范围的非交通枢纽地区，由于受到多个交通枢纽城市的引力作用，实力越小的枢纽城市对中间覆盖地带的交通促进作用越小，对应的交通辐射力越小，相对的交通联系量也越小。

引力函数是距离函数，用于度量两个区域之间引力随距离衰减的规律，这里的距离是广义距离，既可以是几何距离，也可以是交通费用或时间，还可以是这些因素的加权组合。引力函数的概念最早在1931年由赖利根据万有引力理论提出，当时称为“零售引力规律”。之后，康弗斯在“零售引力规律”理论的基础上通过计算给出了断裂点定量的解释。

在上述研究的基础上，现重新定义康维斯断裂点函数。该模型中主要包含两个变量，即交通的客运、货运吞吐能力与交通运输的距离。两地之间断裂点的位置随着上述两个条件变化，断裂点为城市之间交通吸引力的平衡点，断裂点到交通枢纽城市的距离与交通的竞争力正相关。根据实际情况，对模型进行交通化改造：1）用客货运量代替原模型中的“城市质量”，即城市影响力P；2）用连接两地之间的高速公路或快速路长度代替原模型中的空间距离，即DAB。

实际应用过程中，可利用断裂点模式分别计算两城市间的断裂点，然后连接相邻的断裂点，即可确定该城市的吸引范围。目前关于断裂点的连接方法尚无统一的说法，主流方法见表1。平面区域内，voronoi图的类型主要取决于地区城市的待评指标权重，如果地区城市待评指标权重相同，则构成常规voronoi图；若权重不同，则其吸引范围的分界线接近为一条光滑的圆弧，构成加权voronoi图。事实上，对于城市交通而言，权重中指标相同的理想状态基本上不会出现，加权voronoi图法对于区域性交通引力圈而言更适合，故采用加权voronoi图法。

表1　断裂点连接法

断裂点理论的核心内容：城市交通的吸引范围是由城市交通发展规模和两地间的距离决定的，城市交通对其周围地区的影响强度与城市规模及交通发展情况成正比，与到城市中心的距离成反比。定义相邻两城市间的交通吸引与服务能力达到平衡的点为断裂点，根据万有引力定律，其计算方法如下：

式中：K为常数，依实际情况而定；Pi、Pj分别为第i、j座城市的综合交通质量指标值；dij为第i、j座城市间的交通距离，实际运用中常采用各种运输方式中的最短通道里程。

令dA、dB表示“断裂点”离对应两座城市的空间距离，根据式（1）可得：

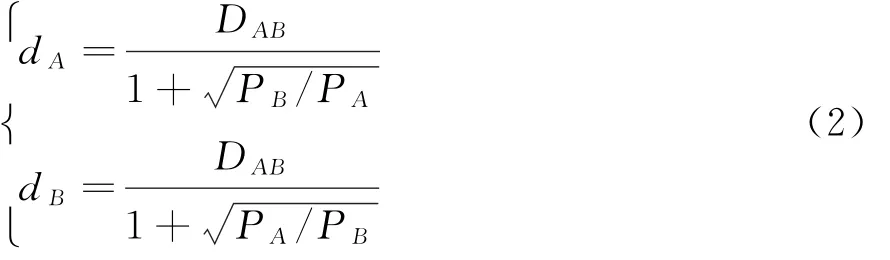
式中：dA、dB分别为断裂点到两城的距离；DAB为两城的交通距离；PA、PB分别为交通的影响力，由经济、人口、交通发展程度权重得到。

2　案例分析

以重庆市为对象，在400km半径范围内测算重庆市交通辐射吸引力，重点考虑重庆市与周边交通枢纽城市的交通辐射竞争关系。因为两座相邻交通枢纽城市对中间地带的区域交通都有吸引力，吸引力强的交通枢纽城市会获取更多的交通量，反之，吸引力弱的交通枢纽城市获取较少的交通量。通过对实际调研与历史数据的分析，将成都、西安、长沙、贵阳这4座距离较近、交通影响较大的城市列为重庆市交通吸引的辐射竞争者。中间地带的交通量按各地交通的竞争辐射力进行分配（见图1）。

图1　重庆与周边重要城市交通吸引辐射示意图（单位：km）

两地间交通吸引力由诸多因素决定，其中最直接的影响因素为两地间交通连接性和地区距离。借用康维斯断裂点模型计算重庆市与周边主要城市之间的交通吸引均衡点，在吸引均衡点周围的交通出行量按照距离重庆主城距离与断裂点距离的比例来计算；交通吸引均衡点两边靠近和远离重庆的地区出行吸引量依次递增或递减。考虑到中国特色的行政区划归属问题，凡是重庆市内的区县，无论其在均衡点的内外，其出行吸引均视为有效，即其所产生交通吸引量全部计入重庆市的交通吸引范围。

依据建立城市交通竞争力评价指标体系的原则，从四方面选取多个指标建立评价城市交通中心性强度的指标体系（见表2）。

表2　城市交通吸引强度的评价指标体系

选用经济水平、城市人口、客货运量作为城市交通吸引力指标，即城市交通吸引力就是由4个指标合成的综合指标。采用几何平均值的方法，把每座城市的4个指标的几何平均值作为该城市的综合规模值V，计算公式为：

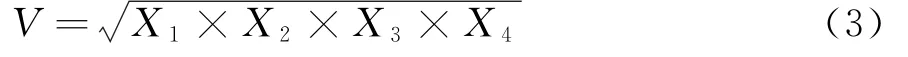
式中：V为某城市的综合交通吸引力；X1为GDP（万亿元）；X2为城市人口（亿人）；X3为货运量（亿t）；X4为客运量（亿人次）。

计算重庆市及周边4座城市的综合规模，计算结果见表3、表4、图2。

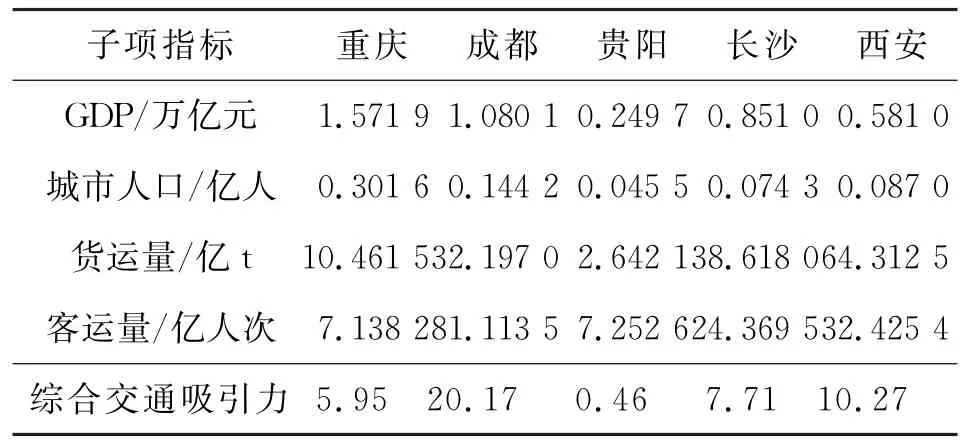
表3　地区综合出行指标

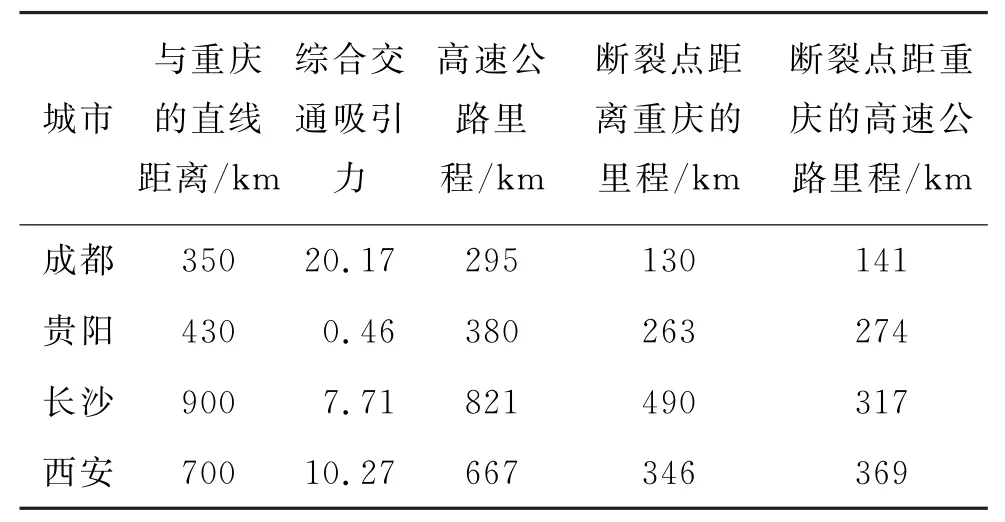
表4　重庆与周边竞争城市中间地带断裂点

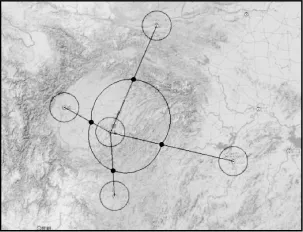
图2　基于加权voronoi图的重庆市吸引范围示意图（单位：km）

在城市综合交通吸引力预测中，充分考虑各地区的现有经济规模和今后的发展速度。在400km辐射半径内，成都方向有德阳、绵阳、乐山、内江、宜宾、自贡、泸州、遂宁、南充等10余座大中城市，其经济规模较大、发展速度较快；西安方向有达州、巴中、广元、汉中、安康等中心城市，其经济规模较小、发展速度较快；长沙方向有张家界、怀化等中心城市，其经济规模较小；贵阳方向有遵义、毕节、安顺、六盘水、昭通等10余座大中城市，其经济规模较大、发展速度略慢。这些城市都是影响未来交通吸引平衡的重要控制点。据此计算重庆交通辐射半径400km以内的主要辐射城市的有效出行吸引力，结果见表5、图3。

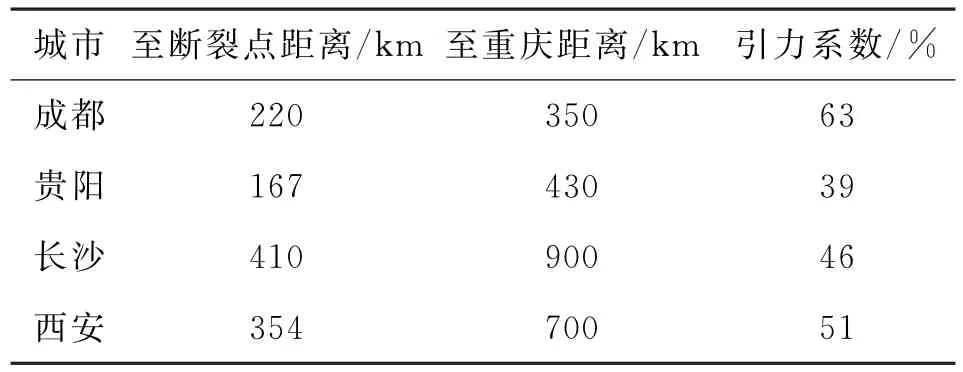
表5　主要辐射城市的有效吸引力

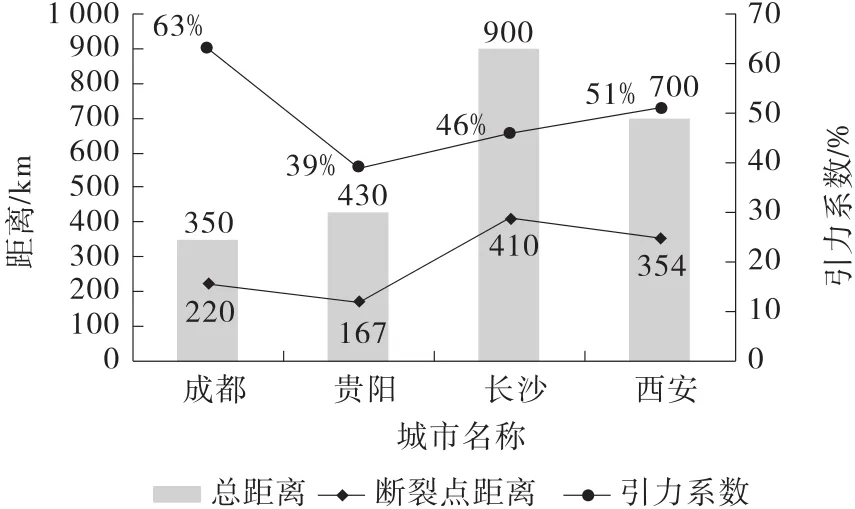
图3　断裂点及引力系数曲线

由表5、图3可知：在重庆及周边地区经济发展水平保持稳定的条件下，对于重庆与成都、西安之间的大中城市，成都与西安的交通引力系数分别达63%、51%，辐射效应高于重庆；对于重庆与贵州、长沙之间的大中城市，重庆的交通引力系数分别为61%、54%，高于贵阳39%、长沙46%。说明重庆对外交通辐射区域主要为渝东南地区及贵州北部地区。因此，为了进一步提升重庆交通吸引辐射范围，支撑重庆打造互联互通重要枢纽，应进一步加强重庆市主城区与渝西地区之间交通运输网络的构建。