基于直接关系图方法的丁酸甲酯燃烧反应机理的框架简化

王全德

(中国矿业大学低碳能源研究院，江苏 徐州221008)

基于直接关系图方法的丁酸甲酯燃烧反应机理的框架简化

王全德*

(中国矿业大学低碳能源研究院，江苏 徐州221008)

由于直接关系图 (DRG)方法的概念简单和计算量较小，使得DRG方法目前已经成为详细燃烧反应机理框架简化的主流方法。DRG方法中评价物种之间依赖关系的相互作用系数和关系图连接权重的计算方法控制着DRG方法的简化效果。采用四种不同形式的相互作用系数的定义方法，分别与标准的DRG搜索算法和基于误差传播的搜索算法 结合，构建了丁酸甲酯的框架燃 烧反应机理。通过系统的误差分析比较了不同简化方法构建的框架机理的模 拟可靠性。重点采用基于元素流量分析的反应路径分析方法研究了框架机理的化学动力学。最后，通过交集的思想构建了一个只包含96个物种的丁酸甲酯框架燃反应机理，并且反应路径分析结果表明丙烯的燃烧化学力学在丁酸甲酯燃烧过程中占有重要地位。本文通过对不同DRG方法的系统比较研究表明了反应路 径分析在框架机 理可靠性验证中 的重要性，对进一步发展更为有 效的框架简化方法提供重要依据 。

燃烧反应机理；直接关系图方法；框架简化；丁酸甲酯

1 Introduction

In the past few years,the developmentof detailed combustion reactionmechanisms of practical fuels has grown by orders of magnitude,and the sizesof thesemechanismsincrease from 10－20species for hydrogen combustion tomore than thousands of species inmany recentdetailedmechanisms for practical fuels1－4. Ithasbeen confirmed thatdetailed reactionmechanismscanprovide moreaccurate predictionsof the combustion propertiesof fuels, including ignition delay times,laminar flame speed,and the formationof pollutionsoverwide rangesof temperature,pressureand compositions5－7.However,incorporating such detailedmechanisms into multidimensional combustion simulations remains a great challenge due to thehugedemandsof computational resourcesand the stiff problem induced by the different timescalesof speciesand reactions in the detailedmechanisms.Therefore,in order tomake numerical simulations of combustion computationally affordable and comprehensively reliable,the developmentof computational methods for rigorous reduction of detailedmechanismsisessential.

The developmentof mechanism reductionmethods hasmade significant progress and a variety ofmethodologies have been developed8,9.Mechanism reduction methods are generally classified into two classes10:the first isskeletal reduction,which directly removes unimportant species and reactions from the detailedmechanism;theotherapproach is timescale reductionwhich is via the decomposition ofmotion in phase space into fastand slow modes.Elim ination of unimportant species and reactions from detailed mechanisms can reduce the computational cost significantly,since the computational costof simulations typically scales quadratically with the number of species,while only linearly with the number of reactions.Therefore,skeletal reduction is typically the first step inmechanism reduction.The detection of unimportant species can be effectively achieved via careful inspection of the Jacobianmatrix,and variousmethods including the computational singular perturbation(CSP)method10－12,level of importance(LOI)13,and connectivity method(CM)14,15have been developed.Another classof approach for specieselimination is based on graph theory,which w as initially introduced by Bendtsen et al.16.In 2005,Lu and Law17devised an automatic mechanism reduction procedure,namely,the directed relation graph(DRG)method based on connectivity graph structures.The DRGmethod can be carried outw ith a linear scaling algorithm; thus,the com putational cost for mechanism reduction scales linearly with the number of species18.Therefore,DRG is particularly suitable as the first step to reduce largemechanisms.Due to the simple concept and low computational cost,the DRG method has been widely used for skeletalmechanism reduction and many modifications and improvements have been made following the pioneeringwork of Lu and Law19－22.

In DRGmethod,the coupling between species is represented by a directed graph,inwhich each vertex denotesa species in the detailedmechanism,and an edge exists from vertex A to vertex B only if the removalof species Bwould directly induce significant error to the production rate of speciesA.The interaction coefficient tomeasure thecoupling effectbetween speciesand thegraph searchmethod is the key factor controlling the definitions and performances of different DRG based methods.After the pioneering work of Lu and Law,Pepiot-Desjardins and Pitsch19introduced the concept of error propagation(EP)in DRG.In addition,the authors also proposed a different definition of the interaction coefficient to improve the performance of themethod. Recently,in order to handle the large isomergroups in biodiesel mechanisms,a revised DRG approachwith a different definition for the interaction coefficient is proposed by Luo etal.20.Further, in order to improve the prediction of reaction fluxes,the so-called path flux analysis(PFA)method was proposed in which both consumption and production pathwayswere used tomeasure the coupling effectbetween species for the skeletal reduction21.

Due to the differencesamong the above DRG basedmethods, when skeletal reduction is performed to the same detailed mechanisms,the differentDRG basedmethodsmay obtain very different skeletalmechanisms23.Generally,the validation of the skeletalmechanism isusually through comparisonsof simulation resultsof combustion propertiesw ith detailedmechanism.On the otherhand,from the chemists′opinions,nomatterwhatmethods havebeen adopted for skeletalmechanism generation,the realistic chem ical kinetics and themajor reaction pathways should be maintained,whichmeans that the resulting skeletalmechanisms should preserve allof the importantspeciesand reactions to avoid some spuriouserror cancellation during numerical simulations24,25. Therefore,a more in-depth analysis of different DRG based skeletal reductionmethods is critical.

Based on the above considerations,in thiswork,we presenta detailed comparison of contemporary DRG based methods.More specifically,four different definitions of the interaction coefficientsin conjunctionwithboth standard DRGand EPgraph search methods are em ployed to construct skeletal mechanism s for methyl butanoate(MB)combustion by the removalof potentially redundantspeciesw ithoutsignificant lossof the accuracy of the detailedmechanism.The detailed combustionmechanism ofMB chosen in thiswork is due to the recent large amounts of utilization of biodiesel,w hichmotivates intense research efforts to achieve a comprehensiveunderstanding of biodiesel combustion chem istry.The combustion chem istry of MB providesa prototype to understand realistic combustion of biodiesel fuels26,27.Particular attentionshave been focused on the chemicalkinetics of the resulting skeletalmechanisms from differentDRG basedmethods.

2 Mechan is　mreduction and analysis methods

2.1DRG based m ethod s

The identification and elimination of unimportantspecies from the detailedmechanisms is complicated due to the coupling of the species.The connectivity graph structures in DRGmethod provide an effective solution for this problem.Fig.1 illustrates thegeneral idea of DRG.In all the DRG basedmethods,the first step is to map the reaction system into a graph structure,in which eachvertex in the graph denotes a species as shown in Fig.1.If the removal of species B directly induces significant error to the production rate of speciesA,then an edge exists from vertex A to vertex B.Thus,how to define the interaction coefficient to evaluate the direct influenceof one specieson another comesout to be the first question in DRG methods.In the original DRG method,the interaction coefficientwasdefined as17:

In order to handle the large isomer groups in biodieselmechanism reductions,Luo et al.20proposed a new definition for the interaction coefficient:

Further,in order to im prove the prediction of reaction fluxes, amore complicated interaction coefficient in the so-called path flux analysis(PFA)methodwasproposed21:

in which

Fig.1 Scheme of the general idea of theDRGmethods

After the definition of the interaction coefficients,a depth first search is performed starting atuser-selected targetspecies(e.g., fuel,oxidizer)to find the dependency pathways for all species relative to the targets17.This procedure is iterated until nomore importantspeciesare chosen and the reducedmechanism is thus generated by including only importantspeciesand reactions.The size of the reducedmechanism is controlled by a threshold value (ε)which decides the existence of the vertex.However,in the standard procedures of DRG,it is assumed that every species selected to be kept in themechanism is equally important,and neglects the connection length between the coupling species.For example,in Fig.1,ifwe selectspecies A as the starting important species,speciesC is recognized as the same importanceasspecies B,which competently neglects the longer connectionway to reach speciesA.In order to overcome thisdeficiency,Pepiot-Desjardins and Pitsch19introduced the EPconcept,in which the interaction coefficient is defined as the productof intermediate interaction coefficients along the connection ways.For example,the interaction coefficientsof rACand rAEin the EP procedure would be calculated asin w hichdenotes the direct interaction coefficient in Fig.1.Pepiot-Desjardins and Pitsch19also defined a new interaction coefficient as follow ing:

It isobvious that the four definitionsof the interaction coefficients can be used in combinationwith both the standard DRG and the EP procedures,providing eight different DRG based skeletal reductionmethodswhich are investigated in the presentwork.

2.2Elem en t flux ana lysis

In the present work,chemical kinetic analysis for MB combustion hasbeen performed in order to check the species retained in the resulting skeletalmechanisms.Theelement flux analysis is used as the reaction path analysismethod and is briefly outlined. In element flux analysis,theelement flux for each element(such as C)from species k1to k2at instantaneous time t is calculated via25:

Consequently,thenormalized weightof element flux from k1to k2to the totalout flux of speciesk1can beeasily derived as

In the presentwork,both theabove DRG basedmethodsand the element flux analysis have been implemented as post-processing programs to dealw ith the results from Chemkin software28.The detailedmechanism for MB combustion isproposed by Dooley et al.29,which consists of 275species and 1549 elementary reactions.To achieve a skeletalmechanism suitable over a wide range of applications,the DRG based methods are applied to reaction state pointsdensely sampled from constantpressureautoignition simulationswithin the parameter rangeof pressure from 1.01×105to 3.04×106Pa and equivalence ratio from 0.5to 2.0. The initial temperature for constantpressureauto-ignition isset to be650－1700K.Ithasbeen previously confirmed that reaction states solely sampled from auto-ignition simulations can exhibit good performance in generating skeletalmechanisms30.

Fig.2 Species retained in the resu lting skeletalmechanism sw ith respect to the threshold valuesby using different DRG basedm ethods

3 Results and discussion

3.1Resu lts o f skeletal reduction

As previously stated,the size of the skeletalmechanism is controlled by a threshold valuewhich decides the existence of the vertex,and the resulting skeletalmechanisms can be traditionally validated via comparing simulation results of combustion propertieswith detailedmechanism.In order to check the performance of the skeletalmechanism for differentcombustion propertiesover a wide range of parameters,the validation procedures should cover the frequently-used combustion properties including ignition,extinction,and laminar flame speed.However,thegenerally used extinction simulations and laminar flame speed only represent high-temperature combustion properties,which cannot reflect the low-temperature combustion chem istry.Therefore, ignition delay time is selected as the only parameter for error control in mechanism reduction,and the error of the reduced mechanism is calculated via the following equation:

whereτign,skelandτign,detrepresent ignition delay time due to the skeletal and detailed mechanisms,respectively.In thiswork,ignition delay time isdefined as the time pointwhen the temperature is increased by 400K com pared w ith the initial tem perature.

Fig.2 shows the number of species retained in the resulting skeletalmechanisms versus the threshold valuesby using the four definitions of the interaction coefficients in conjunction without or w ith the EP procedure,while Fig.3 exhibits the resulting skeletalmechanism sw ith different number of species versus the maximum errorof the predicted ignition delay timeatequivalence ratio(φ)of 1.0and pressure of 2.02×106Pawithin the temperature ranges from 700to 1800K.For the four definitionsof the interaction coefficients in combination with the standard DRG procedure,it can be seen that as the threshold value increases,the numberof species retained in the resulting skeletalmechanisms by using theoriginalDRGmethod17decreases faster than theother three definitions.The results derived from the revised definition by Luo et al.20tend to be very stable as the threshold value increases.However,from Fig.3,it is obvious that the definition proposed in the PFAmethod shows thebest reduction results.The maximum relativeerror in the predicted ignition delay time isstill w ithin 10%even though the number of species retained in the skeletalmechanism has been reduced to be 104.For the four definitionsof the interaction coefficients in conjunction w ith the EPprocedure,thenumberof the species in the derived skeletal mechanisms decreasesmuch steeper as the threshold value increases.From the predicted error analysis of the ignition delay time as shown in Fig.3,it can be seen that the two definitions proposed in the PFA and original DRGEPmethods19exhibitbetter performance than the definitions in theoriginal and Luo′s revised DRGmethods.The critical reason for the different performances in the resulting skeletalmechanism s is due to the species selections by the different definitions,and the combustion chemical kinetics inwhich degree can be captured by the skeletalmechanisms directly controls the performance of the skeletalmechanisms.Therefore,in thenextsection,amore in-depth analysisby combining systematic error analysisand chem ical kinetic analysis has been performed to check the robustness of the resulting skeletalmechanisms via differentDRG basedmethods.

3.2Robustness analysis o f the skeletalm echanism

In order to check the reliability of the resulting skeletal mechanisms,robustnessanalysesof the skeletalmechanisms have been performed through systematic erroranalysis of the predicted ignition delay time under aw ide range of simulation conditions. Figs.4and 5demonstrate theerroranalysis resultsof the predicted ignition delay timesunder certain simulation conditionsby em-ploying the chosen resulting skeletalmechanism s derived from different reductionmethods.The retained species in the corresponding skeletalmechanism togetherw ith the threshold value at which the skeletalmechanism isadopted arealso explicitly shown in Figs.4and 5.It can be seen that the relative errorsof the predicted ignition delay timesunder the selected simulation conditions via all the resulting skeletalmechanisms arew ithin 15%, indicating thegood performancesof the skeletalmechanisms.It isalso noted that themaximum errorsusually occur at fuel-lean combustion conditions.Further,it should be noted that when skeletalmechanismswithmuch less speciesareused,the relative errorsof the predicted ignition delay times tend to increasemore than 20%at some simulation conditions.Thus,the selected skeletalmechanisms used in Figs.4and 5seem to be the best candidate skeletal mechanisms derived from corresponding reductionmethods.

Fig.3 Skeletalm echan ism sw ith different num ber of species versus themaximum error of thepredicted ignition delay time

Fig.4Relativeerrorsof predicted ignition delay timesusing resu lting skeletalmechanism s from the four DRG m ethodsw ithou t EPprocedure under certain sim u lation conditions

3.3Reac tion path analysis

Besides robustness analysis of the skeletalmechanism via different reductionmethodsbased on systematic error analysis, reaction path analysis by em ploying the detailedmechanism has been performed to understand the realistic combustion chem istry processes.Time-integrated element flux analysishasbeen adopted to perform reaction path analysis in simulationsof the constantvolume ignition processes.Fig.6shows themajor initial reaction paths during the oxidation of MB atdifferent temperatures.The percentages of the conversions(Figs.4－6)calculated from the detailedmechanism from top to bottom represent theanalysis at initial temperatures of 700,900,and 1200K w ith equivalence ratio of 1.0and pressureof 1.01×105Pa.The percentageof the conversions isdefined as the percentageof the flux of elementC from one species to anotherw ith respect to the total flux of C.From Fig.6,itcan be seen that the initial reaction path forMB is dominantby the H-abstraction reactions to the formation of corresponding fuelalkyl radicals,namely,MBMJ,MB2J,MB3Jand MB4J.The directpyrolysis reactionsofMB to the formation of BAOJwith CH3(methyl radical)and ME2Jw ith C2H5(ethyl radical)only play aminorpart.The following step is theβ-scission reactions of the fuel alkyl radicals to the formation of small molecules,which proceed very fast.There are a number of reaction channels through which MB2J can decompose,but the pyrolysis reaction ofMB2Jto the production of MP2D with CH3isdominant.ForMBMJ,the following step is almostcompletely controlled by theβ-scission reaction to the formation of formaldehyde(CH2O)and the NC3H7CO radical.MB3J and MB4J undergo similar reaction path to MBMJ,and theβ-scission reaction controls the following step.Itshould be noted thatat low temperatures,the primary fuel alkyl radicals also undergo the abstraction reaction of an O atom from HO2or RO2(e.g.,CH3O2) to the formation of“MBXO”,which represents the fouralkoxyradicals.Fig.7 exhibits this phenomenon via instantaneous element flux analysisat700and 1200K(the initial temperatureof the simulation is680K w ith equivalence ratio of 1.0and pressure of 1.01×105Pa.),which clearly demonstrates the different reaction paths of the four alkoxy radicals at low and high temperatures.The results of reaction path analysis are also in good agreementwith the results via flux analysis by Dooley et al29. Figs.8－9 show the reaction path analysis results forMP2D and C3H6(propene),which are important intermediates during combustion processesofMB.ForMP2D,there area largenumberof reaction channels to undergo pyrolysis,and the C2and C3species constitutes themajor products.The reaction paths for C3H6and other related smallmolecules including C2H4(ethylene)and C2H2(acetylene)are shown by Fig.9.The result is also in good agreementwith previousstudies25,29.

Fig.5Relative er rors of predicted ignition delay tim es using resulting skeletalm echanism s from the four DRGmethodsw ith EP proceduresunder certain simu lation conditions

Fig.6Time-integrated element flux analysisofMB during constant volume auto-ignition processes

Fig.7 Initial reaction path for MB via instantaneouselement flux analysisat700K(up)and 1200K(down)

Fig.8 Time-integrated element flux analysisofMP2D during constant volume au to-ignition processes

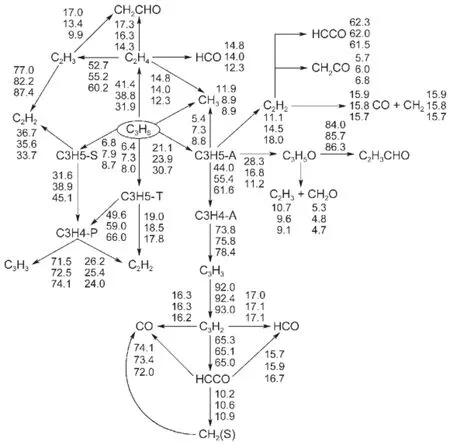
Fig.9 Tim e-integrated elem en t flux analysis results of C3H6during constan tvolum eauto-ign ition processes

Given the reaction pathanalysis results via detailedmechanism, in order to check the chem ical reality of the resulting skeletal mechanisms from different reductionmethods,the retained species in differentskeletalmechanismsw ith the predicted errorsof ignition delay time controlled at the same levelare compared in detail.Table 1 lists the species retained in the corresponding skeletalmechanisms derived from different reductionmethods. There are 96species retained in all the skeletalmechanisms,and the differentspeciesare explicitly given in Table1.From Table1 togetherwith the previous reaction path analysis,it can be seen that the speciesneeded to describe themajor initialoxidation path of MB including the primary fuel alkyl radicals and the alkoxyradicals are well-reserved in all the skeletalmechanisms.The differencesof the species among these skeletalmechanisms are mainly due to the C3species.From the reaction path analysis,it is obvious that the species to describe the oxidation of C3H6and other related smallmolecules are also covered by the96species existing in all skeletalmechanisms,w hich raises an interesting problem thatwhether the skeletalmechanism comprising of the 96species can be agood candidate skeletalmechanism forMB combustion.Fig.10shows the relative errorsof predicted ignition delay times by using the 96species skeletalmechanism under varioussimulation conditions.Clearly,the ignition delay time can be w ell predicted by the 96species skeletalmechanism and the maximum error is controlled w ithin 10%,indicating the good performance of the 96species skeletalmechanism.In order to further check the robustnessof the96speciesskeletalmechanism, laminar flame speed simulations are carried out by using the detailed and 96species skeletalmechanism,respectively.Fig.11 show s the lam inar flame speed asa function of the equivalence ratio atpressuresof 1.01×105Paw ith initial inlet temperature of 400K.It can be seen that the skeletalmechanism also predicts the laminar flame speed accurately compared w ith the detailed mechanism,indicating that the96speciesskeletalmechanism also exhibits good performance in flame simulations.To further demonstrate the performanceof the skeletalmechanism,species profiles in perfectly stirred reactor are also compared between detailed and reduced skeletalmechanism.Fig.12 shows the calculatedmole fraction of some important speciesas a function oftem perature using the detailed and skeletal mechanisms,respectively,with equivalence ratio of 1.0ata pressureof 1.01×105Pa,and residence time of 0.07 s.It can be seen that themole fractions of important species resulting from the skeletalmechanism are still rather close to those from the detailedmechanism, indicating the good performance of the 96species skeletal mechanism.Itshould benoted that the currentskeletalmechanism isnotdirectly reduced forapplications in practical computational fluid dynamics simulations,and itshould be further reduced via themethod of quasi-steady stateapproximation and so on in order to be used for engine designs.

Table1 Retained species in the corresponding skeletalm echanism sw ith the predicted errors of ignition delay tim e controlled w ithin 15%

Fig.10Relativeerrorsof predicted ignition delay timesusing the 96speciesskeletalmechanism under varioussimu lation conditions

Fig.11 Lam inar flame speed versus equivalence ratio p redicted by the detailed and 96species skeletalm echanism

Fig.12 Mole fraction ofmajor speciesasa function of tem perature via detailed(lines)and 96species skeletalmechanism(symbols)

4Conclusions

In the present work,w ithin the DRG framework,detailed comparisons of contemporary DRG basedmethods for skeletal reduction of detailed combustion mechanisms have been performed.Specifically,four contemporary different definitions of the interaction coefficients in conjunction w ith both standard DRG and EPgraph searchmethods are considered and employed to constructskeletalmechanisms forMB combustion by removing potentially redundant species w ithout significant loss of the accuracy of the detailedmechanism.Particularattentionshavebeen focused on the retained species in the resulting skeletalmechanisms from different DRG based methods.Major findings and conclusionsof thiswork are summarized as follows.

(1)Although the errorsof predicted combustion properties by using skeletalmechanism s derived from different DRG based methods are controlled at the same level,the retained species in these skeletalmechanisms generated from different DRG based methods remains different due to the different selections of importantspecies.

(2)A more in-depth analysis by combining systematic error analysis and chemical kinetic analysis has been performed to check the robustness of the resulting skeletalmechanisms via different DRG basedmethods.The PFAmethod and theoriginal DRGEPmethod proposed by Pepiot-Desjardinsand Pitsch exhibit better performance among the DRG basedmethods studied in this work.

(3)All of the skeletalmechanisms generated from different reduction methods demonstrate good performance in both predicting combustion properties and reserving chem ical kinetics. How ever,none of the DRG basedmethods can directly create an optimalskeletalmechanism retaining all the important properties of the detailedmechanism butwith the leastspecies,implying that there isstilla possibility to further improve the DRG approach.

(4)Reaction path analysis of reduced skeletalmechanisms is necessary beyond comparisonsof simulation resultsw ith detailed mechanism.It isworth noting thatonly the resultsof reaction path analysisbased on detailedmechanism are explicitly shown in this work because the importantspeciesdemonstrated via reaction path analysisareall retained in the reduced skeletalmechanisms and they account for nearly one hundred percentage of the conversions ofmajor species,which indicates that the resultsof reaction path analysis from skeletalmechanisms are nearly identical to the detailedmechanism.

(5)A 96species skeletalmechanism for MB combustion is obtained via the idea of intersection of skeletalmechanisms from different reductionmethods and further validated through simulations of key combustion properties.Reaction path analysis highlights the importance of propene chemistry during MB oxidation.

Acknow ledgment:We thank National Supercomputing Center in Shenzhen for providing the computational resources and Chemkin software(v.15131).

References

(1)Simmie,J.M.Prog.Energy Combust.Sci.2003,29,599.doi: 10.1016/S0360-1285(03)00060-1

(2)Wang,Q.D.RSC Adv.2014,4,4564.doi:10.1039/c3ra45959d

(3)Guo,J.J.;Hua,X.X.;Wang,F.;Tan,N.X.;Li,X.Y.Acta Phys.-Chim.Sin.2014,30,1027.[郭俊江,华晓筱,王繁,谈宁馨,李象远.物理化学学报,2014,30,1027.]doi:10.3866/ PKU.WHXB201404031

(4)Westbrook,C.K.;Pitz,W.J.;Herbinet,O.;Curran,H.J.; Silke,E.J.Combust.Flame2009,156,181.doi:10.1016/j. combustflame.2008.07.014

(5)Battin-Leclerc,F.;Blurock,E.;Bounaceur,R.;Fournet,R.;Glaude,P.A.;Herbinet,O.;Sirjeana,B.;Wartha,V.Chem. Soc.Rev.2011,40,4762.doi:10.1039/C0CS00207K

(6)Battin-Leclerc,F.Prog.Energy Combust.Sci.2008,34,440. doi:10.1016/j.pecs.2007.10.002

(7)Xu,J.Q.;Guo,J.J.;Liu,A.K.;Wang,J.L.;Tan,N.X.;Li,X. Y.Acta Phys.-Chim.Sin.2015,31,643.[徐佳琪,郭俊江,刘爱科,王健礼,谈宁馨,李象远.物理化学学报,2015,31, 643.]doi:10.3866/PKU.WHXB201503022

(8)Lu,T.F.;Law,C.K.Prog.Energy Combust.Sci.2009,35, 192.doi:10.1016/j.pecs.2008.10.002

(9)Fang,Y.M.;Wang,Q.D.;Wang,F.;Li,X.Y.Acta Phys.-Chim.Sin.2012,28,2536.[方亚梅,王全德,王繁,李象远.物理化学学报,2012,28,2536.]doi:10.3866/PKU. WHXB201208201

(10)Valorani,M.;Creta,F.;Goussis,D.A.;Lee,J.C.;Najm,H.N. Combust.Flame 2006,146,29.doi:10.1016/j. combustflame.2006.03.011

(11)Valorani,M.;Creta,F.;Donato,F.;Najm,H.N.;Goussis,D.A. Proc.Combust.Inst.2007,31,483.doi:10.1016/j. proci.2006.07.027

(12)Prager,J.;Najm,H.N.;Valorani,M.;Goussis,D.A.Proc. Combust.Inst.2009,32,509.doi:10.1016/j.proci.2008.06.074

(13)Løvås,T.Combust.Flame 2009,156,1348.doi:10.1016/j. combustflame.2009.03.009

(14)Nagy,T.;Turányi,T.Combust.Flame 2009,156,417.doi: 10.1016/j.combustflame.2008.11.001

(15)Zsély,I.G.;Nagy,T.;Simmie,J.M.;Curran,H.J.Combust. Flame 2011,158,1469.doi:10.1016/j. combustflame.2010.12.011

(16)Bendtsen,A.B.;Glarborg,P.;Dam-Johansen,K.Computers& Chemistry2001,25,161.doi:10.1016/S0097-8485(00)00077-2

(17)Lu,T.F.;Law,C.K.Proc.Combust.Inst.2005,30,1333.doi: 10.1016/j.proci.2004.08.145

(18)Lu,T.F.;Law,C.K.Combust.Flame 2006,144,24.doi: 10.1016/j.combustflame.2005.02.015

(19)Pepiot-Desjardins,P.;Pitsch,H.Combust.Flame2008,154, 67.doi:10.1016/j.combustflame.2007.10.020

(20)Luo,Z.Y.;Lu,T.F.;Maciaszek,M.J.;Som,S.;Longman,D. E.Energy Fuels2010,24,6283.doi:10.1021/ef1012227

(21)Sun,W.;Chen,Z.;Gou,X.;Ju,Y.Combust.Flame 2010,157, 1298.doi:10.1016/j.combustflame.2010.03.006

(22)Jiang,Y.;Qiu,R.Acta Phys.-Chim.Sin.2009,25,1019.[蒋勇,邱榕.物理化学学报,2009,25,1019.]doi:10.3866/ PKU.WHXB20090426

(23)Tosatto,L.;Bennett,B.A.V.;Smooke,M.D.Combust.Flame 2013,160,1572.doi:10.1016/j.combustflame.2013.03.024

(24)Wang,Q.D.Energy Fuels2013,27,4021.doi:10.1021/ ef4007774

(25)Wang,Q.D.;Fang,Y.M.;Wang,F.;Li,X.Y.Proc.Combust. Inst.2013,34,187.doi:10.1016/j.proci.2012.06.011

(26)Fisher,E.M.;Pitz,W.J.;Curran,H.J.;Westbrook,C.K.Proc. Combust.Inst.2000,28,1579.doi:10.1016/S0082-0784(00) 80555-X

(27)Coniglio,L.;Bennadji,H.;Glaude,P.A.;Herbinet,O.; Billaud,F.Prog.Energy Combust.Sci.2013,39,340.doi: 10.1016/j.pecs.2013.03.002

(28)Chemkin,v.15131;Reaction Design:San Diego.

(29)Dooley,S.;Curran,H.J.;Simmie,J.M.Combust.Flame 2008, 153,2.doi:10.1016/j.combustflame.2008.01.005

(30)Wang,Q.D.;Fang,Y.M.;Wang,F.;Li,X.Y.Combust.Flame 2012,159,91.doi:10.1016/j.combustflame.2011.05.019

Skeletal Mechanism Generation for Methyl Butanoate Combustionvia Directed Relation Graph Based Methods

WANG Quan-De*
(Low Carbon Energy Institute, China University of Mining and Technology, Xuzhou 221008, Jiangsu Province, P. R. China)

Directed relation graph (DRG) based skeletal reduction methods have become the mainstreamapproach for skeletal mechanism generation because of their simple concept and low computational cost. Withinthe DRG framework, the definitions of the interaction coefficients and the connection weights in different DRGmethods control the resulting skeletal mechanisms. In this work, based on DRG methods, four contemporarydefinitions of the interaction coefficients in conjunction with both standard DRG and error propagation (EP) graphsearch methods are used to derive skeletal mechanisms for methyl butanoate (MB) combustion. Detailedcomparisons of contemporary DRG based methods are performed by systematic error analysis. To furtherevaluate the performance of the different DRG-based methods, reaction paths are investigated via element fluxanalysis to check the chemical kinetics of the resulting skeletal mechanisms. Furthermore, a 96-species skeletalmechanism for MB combustion is proposed. Reaction path analysis highlights the importance of propenechemistry during MB oxidation. This work reveals the applicability of reaction path analysis in skeletal reductionusing different DRG-based methods, and also provides critical information for further development of skeletalreduction methods.

Combustionmechanism; Directed relation graphmethod; Skeletal reduction; Methyl butanoate

October 15, 2015; Revised: December 18, 2015; Published onWeb: December 21, 2015.

O643

10.3866/PKU.WHXB201512211

**Corresponding author. Email: wqd198686@126.com.

The project was supported by the Fundamental Research Funds for the Central Universities of China (2013QNA08) and National Natural ScienceFoundation of China (21403296).

中央高校基本科研业务费专项资金(2013QNA08)和国家自然科学基金(21403296)资助项目