基于SEM的武器装备体系作战能力关联关系判定方法

陆皖麟，何新华，屈　强，高　飞

(1.装甲兵工程学院信息工程系，北京　100072； 2. 95942部队，武汉　430313)



基于SEM的武器装备体系作战能力关联关系判定方法

陆皖麟1，何新华1，屈强1，高飞2

(1.装甲兵工程学院信息工程系，北京100072； 2. 95942部队，武汉430313)

武器装备体系作战能力组成单元众多，单元间关联关系复杂，造成该问题难以仿真模拟研究。针对这一现状，尝试运用结构方程模型法(SEM)对体系作战能力组成单元间的关联关系进行判定，分析了SEM的基本原理和运用SEM的具体步骤，实例分析表明了该方法的有效性。该方法对准确建立合理的仿真模型有一定的意义。

武器装备体系作战能力；仿真模型；关联关系；结构方程模型法

本文引用格式：陆皖麟，何新华，屈强，等.基于SEM的武器装备体系作战能力关联关系判定方法[J].兵器装备工程学报，2016(8):38-42.

体系作战能力各个组成单元间所存在着复杂的关联关系，是体系作战能力呈现出整体涌现性和非线性的根本原因。因此，对作战能力组成单元间关联关系进行准确判定成为体系作战能力仿真评估工作的重中之重。传统的体系作战能力单元关联关系主要依据专家评估思想得出，此类方法既费时费力又存在巨大的主观性。故而亟需一种新型的更加科学客观的关联关系判定方法以弥补传统方法的不足。

1　结构方程模型法

结构方程模型法(structural equation modeling， SEM)是一种应用统计学领域分析多元数据关联关系的方法[1-2]。结构模型方法是统计学众多方法的综合[3]，包含了多元回归(multiple regression)、因子分析(factor analysis)和路径分析(path analysis)等方法的思想。

SEM虽然属于多元统计理论的一种，但其有着显著的优点[4-5]：① 结构方程分析可同时考虑并处理多个因变量; ② 结构方程分析容许自变量和因变量均含测量误差; ③ 结构方程分析可同时估计因子结构和因子关系。对于武器装备体系作战能力这一复杂系统，运用结构方程模型法探究其作战能力组成单元间的关联关系具有一定意义[6]。

1.1基本概念

为更好地理解SEM，需要对SEM中的若干重要概念加以说明[7-8]：

1) 变量

结构方程模型中对变量的定义主要分为两大类：隐变量和显变量。隐变量指具有不可直接观测特征的综合性变量。显变量是隐变量的相对概念，即可以直接观测得到的变量。针对研究对象的具体属性，可进一步细分为：外生隐变量ξ、内生隐变量η、内生指标变量Y和外生指标变量X。

2) 方程

在结构方程模型中，模型方程主要有3组，包含两方面的内容。一是测量方程，一是结构方程。其中，显变量与隐变量之间的关系用测量方程体现，而隐变量之间的关联关系依据结构方程具体表述。

3) 协方差阵

结构方程模型方法中一项核心的步骤是求解出各个变量的协方差阵[9]。运用协方差具体运算两个变量间观测值与其均值离差的期望，借此来展现两个变量间的关系强弱。在结构方程模型法中，以此来界定变量之间的关系。协方差越大，表明两个变量之间的相关程度越高。

4) RAM图

RAM图全称为Reticular Action Modeling图，是结构方程模型方法中表达估计模型关系的图形。RAM图经过对具体问题的分析后绘出，RAM图是结构方程中表达建模结果最有效的形式。

1.2结构方程模型法的求解思路

结构方程模型法的求解同样运用上述思想，具体步骤为：运用RAM图的结构推导出估计协方差阵，使其与样本协方差阵的差异最小[11]。如果估计模型是正确的，则估计协方差阵与样本协方差阵存在以下关系：

式中:∑表示样本协方差阵；∑(θ)表示估计协方差阵，两个矩阵相等，则其相应位置元素相等，求解出待估计的参数矩阵θ。

进一步推导可得：

若Θε=0，Θδ=0，ΛX=Ιp，ΛY=Ιq，则上式的可测变量无测量误差形式为：

在求解出估计协方差和样本协方差后，模型估计的主要思想就是通过迭代的方法找到一组参数，使得样本协方差和通过模型结构推导出的估计协方差的差异最小。

2　基于结构方程模型法的关联关系求解方法

依据上述求解思想，基于结构方程模型法的武器装备体系作战能力组成单元间关联关系求解步骤可分为以下几步：

1) 采集处理样本数据

结构方程模型法作为一种应用统计学方法，运用的前提是收集到大量统计样本数据。结构方程模型法对样本数据的精准方面，要求比较宽松，允许样本存在误差。一般情况下，样本量应大于300，最好的情况是样本量是未知参数的5～10倍。体系作战能力的各种测量样本，应选用来自于实兵演练和各种武器装备性能指标的真实数据。在获取样本数据后，如果数据存在噪音或过于繁杂，应对数据进行进一步处理。

2) 关联关系的求解

关联关系的估计求解中，可细化为以下两步：

a) 关联关系模型的构建与识别

深入理解武器装备体系，根据领域专业知识，构建体系作战能力组成单元间的关联关系，画出RAM图。由RAM图的拓扑结构得到假设的体系作战能力组成单元间关联关系。

对模型的识别就是检验该模型中的未知参数是否可以进行估计，识别规则主要有t规则。由于在SEM中，共有(p+q)个显变量，可以产生(p+q)(p+q+1)/2个不同的方差和协方差，进而得到(p+q)(p+q+1)/2个不同的含未知参数的方程。因此只要待估计的未知参数的个数满足公式t<(p+q)(p+q+1)/2，方程就是可识别的。其中，t是待估计的未知参数的个数；p是内生显变量的个数；q是外生显变量的个数。

b) 关联关系模型的估计

通过假设的体系作战能力组成单元间关联关系，进一步求解出待估计参数的协方差矩阵。随后通过获取的样本数据，计算得出样本的协方差阵。随后通过迭代的方法，找到一组模型参数，使得样本协方差与估计协方差差异最小。

在结构方程模型法中，将寻找一组模型参数，使得样本协方差与估计协方差差异最小的过程称为模型的估计。模型的估计方法一般有5种：极大似然估计法、广义最小二乘法、加权最小二乘法、渐进自由分布法和马尔科夫链蒙特卡洛法。其中，最常用的方法为极大似然估计法。

极大似然估计法的求解思想是：列出多元正态分布的概率密度函数，迭代出一组模型参数，使得概率密度函数最大。即出现样本协方差与估计协方差差异最小这种情况的概率最大。

具体做法为：列出多元正态分布概率密度函数：

其中，∑为总体协方差阵，内生指标变量X和外生指标变量Y的数量分别为p、q，Ζ则是一个(p+q)×1的向量。

所以，出现一组观测值Ζi的概率为

假定各样本观测值之间互相独立，则出现所有观测值的联合密度函数为

即：

∵x′Ax=tr(x′Ax)=tr(Axx′)

其中S为样本协差阵。

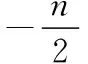
3) 关联关系模型的评价

通过迭代求解出θ后，需要对求解出的模型进行评价。结构方程模型法规定了3类模型评价指标[12]：绝对拟合指标、增量拟合指标和节俭拟合指标。绝对拟合指标直接对估计协方差和样本协方差的拟合程度进行评价，增量拟合指标主要通过测度模型改进拟合的程度来评价指标，节俭拟合指标则运用成本收益的思想，定义估计参数的数量为成本，以拟合程度为收益，通过追求净收益最大化的思想来评价模型。

4) 关联关系模型的修正

在模型关联关系的显示结果中，用单元间的路径表征其间的关联关系，单箭头表示作用关系，双箭头表征关联关系，正值表示正相关，负值表示负相关。经过评价指标的综合评价后，需要对其中不符合实际的部分进行修改。总的来说，模型修改一般针对以下几种情形：

a) 绝对拟合指标中x2值过大。

当评价指标中x2值过大，说明模型没有拟合数据，即所表征的单元间关联关系不符合实际要求。此时应从检查参数估计结果和软件提示信息两方面着手修正。主要措施为检查数据的峰度和偏态。如果存在很高的峰度和明显的偏态，应在保留数据信息的前提下对数据进行变换。

b) 单元间关联关系表述不正确。

在模型关联关系分析结果中，明显不符合实际存在的关联关系，其数值一般显示为一个无法进行标准化的数值，对于这样的关联关系，应予以删除。

c) 残余关联关系。

残余关联关系指的是单元间虽然存在路径，即存在理论上的关联关系。但其数值很小(一般以±0.01为阈值)可以忽略不计的，这样的单元间关联关系也应予以删除。

3　实例分析

上文阐述了体系作战能力组成单元间关联关系的判定方法，对于此种方法的实际运用，一般通过基于结构方程模型法的思想设计的数据处理软件对数据进行处理。主流的运用软件一般有LISREL和Amos。本文将以Amos为平台，判定体系作战能力中战术信息分发能力和网络覆盖能力、网络适应能力之间的关系，展示上述理论的具体应用。主要分为以下几步：

1) 建立作战能力指标体系

建立战术信息分发能力和网络覆盖能力、网络适应能力的指标体系，如图1所示。

2) 关联关系模型的构建与识别

建立战术信息分发能力和网络覆盖能力、网络适应能力的SEM，如图2所示。

图2中变量对应的指标如表1所示。

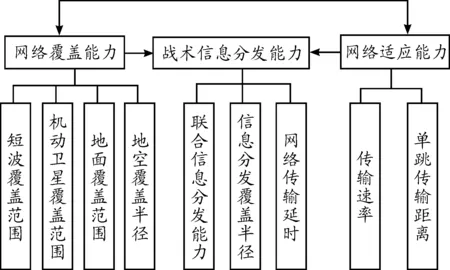
图1　战术信息分发能力的指标体系

图2　战术信息分发能力的SEM

隐变量显变量外生变量ξ1ξ2网络覆盖能力网络适应能力x1短波覆盖范围x2机动卫星覆盖范围x3地面覆盖范围x4地空覆盖半径x5传输速率x6单跳传输距离内生变量η战术信息分发能力y1联合信息分发能力y2信息分发覆盖半径y3网络传输延时

模型的结构方程为：

模型的测量方程为：

上述模型中有6个外生显变量(用p表示)，3 个内生显变量(用q表示)，24 个未知参数，根据t规则，t=24≤(p+q)(p+q+1)/2=45，所以模型是可识别的。

3) 作战能力仿真数据

在某陆军数字化装备仿真试验中心，采用蒙特卡洛法[13]仿真计算不同方案下战术信息分发能力、网络覆盖能力、网络适应能力的指标值，如表2所示。

4) 参数估计结果

将各方案的指标仿真数据的协方差矩阵及战术信息分发能力的SEM 输入Amos，采用极大似然法进行参数估计，得到模型的路径图及各参数的估计值。

根据 SEM 参数估计值，得到战术信息分发能力和网络覆盖能力、网络适应能力之间的关联关系模型为：

模型的部分拟合优度检验结果如图3所示。图3中的拟合指数均处于合理范围之内，故模型是合理的。

图3　拟合优度检验结果

经专家评估和部队调研，此战术信息分发能力和网络覆盖能力、网络适应能力之间的关联关系模型符合部队演练实际情况。

表2　能力指标值

4　结论

对武器装备体系作战能力仿真模型中各个组成单元间关联关系的准确判定是建立合理仿真模型的关键。本研究详细展示了运用SEM判定模型组成单元间关联关系的理论基础和具体步骤。实例分析说明了该方法的工程价值，对仿真模型组成单元间关联关系的判定起到一定的参考作用。

[1]吴兵福.结构方程初步研究[D].天津：天津大学,2006.

[2]GELMAN A.Inference and monitoring convergence.In W.R.Gilks,S.Richardson and D.J.Spiegelhalter (eds),Markov Chain Monte Carlo in Practice[M].London:Chapman and Hall,1996.

[3]GELMAN A,MENG X L,STEM H.Posterior predictive assessment of model fitness via realized discrepancies[J].Statistica Sinica,1996(6):733-759.

[4]黄芳铭.结构方程模型理论与应用[M].北京:中国税务出版社,2005.

[5]邱皓政,林碧芳.结构方程模型的原理与应用[M].北京:中国轻工业出版社,2008.

[6]罗小明,朱延雷,何榕.基于SEM的武器装备作战体系贡献度评估方法[J].装备学院学报,2015(5):1-6.

[7]GELMAN A,ROBERTS G O,GILKS W R.Efficient Metropolis jumping rules.In J.M.Bemardo.J.O.Bergen A.P.Dawid and A.F.M.Smith,Bayesian Statistics 5[M].Oxfod:Oxford University Press,1995.

[8]GEYER C J.Practical Markov chain Monte Carlo[J].Statistical Science,1992,7:473-511.

[9]寇鹏.基于非线性结构方程模型的公司成长性分析[D].昆明：昆明理工大学,2013.

[10]余建英,何旭宏.数据统计分析与SPSS应用[M].北京:人民邮电出版社,2003.

[11]林嵩.结构方程模型原理及AMOS应用[M].湖北:华中师范大学出版社,2008.

[12]程霞.电子零售商采纳供销直供模式的影响因素研究[D].天津：南开大学,2010.

[13]康崇禄.国防系统分析方法[M].北京:国防工业出版社,2003.

(责任编辑杨继森)

Research on Determining Method for Relationship of Armament Combat Capability Based on SEM

LU Wan-lin1, HE Xin-hua1, QU Qiang1, GAO Fei2

(1.Department of Information Engineering, Academy of Armored Forces Engineering,Beijing 100072, China; 2.The No. 95942ndTroop of PLA, Wuhan 430313, China)

The combat capability of armament system is constructed by various units and with complex relationship between units, which makes it difficult in carrying out simulation research. In order to solve this situation, this paper tried to determine relationships between the various components of the armament combat capability by SEM. The basic principle of SEM and the specific application of SEM processes were discussed in detail, and then the instance analysis was given to prove the effectiveness of the method. This method has certain significance for accuratly establishing a reasonable simulation model.

combat capability of armament system; simulation model; relationship; structural equation model

2016-02-11；

2016-03-10

陆皖麟(1992—)，男，硕士研究生，主要从事计算机仿真技术研究。

10.11809/scbgxb2016.08.009

format:LU Wan-lin, HE Xin-hua, QU Qiang, et al.Research on Determining Method for Relationship of Armament Combat Capability Based on SEM[J].Journal of Ordnance Equipment Engineering,2016(8):38-42.

TP391.9

A

2096-2304(2016)08-0038-05

【装备理论与装备技术】