轮毂处边界约束对扭力梁悬架系统低阶模态的影响分析*

高继东　李洪亮　王海洋（中国汽车技术研究中心，天津300300）

轮毂处边界约束对扭力梁悬架系统低阶模态的影响分析*

高继东李洪亮王海洋
（中国汽车技术研究中心，天津300300）

以某车型后扭力梁悬架系统为研究对象，应用有限元法研究轮毂处边界约束强、弱对其低阶模态频率的影响规律。建立轮毂处由钢制夹具约束的悬架系统有限元模型，计算其约束模态并与试验模态结果对比以验证模型的置信度。分析并比较轮毂处采用固定约束、钢制夹具约束、木质夹具约束以及弹性衬套约束4种方式的悬架系统约束模态频率分布。结果表明，当轮毂处边界约束作用由强变弱时，悬架结构的1阶约束模态频率增大，而2阶约束模态频率先减小后增大。

主题词：扭力梁悬架系统轮毂边界约束模态

1 前言

路面激励经悬架系统传递至车身引起振动，严重时会削弱整车NVH性能［1～4］。近年来，扭力梁悬架系统因结构简单、性价比高等优点，广泛应用于中低端乘用车后悬架系统。

目前的工程实践中，越来越多地采用有限元等仿真方法进行悬架结构模态的计算分析，其约束处理较难解决。为建立精确而高效的约束处理准则，需要对约束影响规律进行深入研究，有许多研究者进行了卓有成效的探索。李欣冉［5］、何艳则等［6］建立了某型汽车刚柔耦合动力学模型，针对橡胶衬套对悬架NVH性能的影响，以簧载质量垂向加速度均方根值（RMS）为指标，应用DOE技术进行了衬套灵敏度分析，结果表明扭力梁纵臂前端衬套Y向刚度对垂向振动的影响最为灵敏；陈晓新等［7］也针对扭力梁悬架橡胶衬套进行了灵敏度分析，其评价指标考虑了车辆质心处3个方向的振动，结果表明减振器上端衬套Z向刚度以及扭力梁纵臂前端衬套X向和Z向刚度对车辆总体振动情况的影响最为灵敏。这些研究成果对于衬套约束的正确处理具有指导意义。然而，对于施加在轮毂处的轮胎约束，由于轮胎自身结构及动态特性的复杂性，针对一般衬套约束的处理原则并不能很好地移植应用。为摆脱这一被动局面，需要研究轮毂处边界约束对悬架结构模态的影响规律。由于某车型的扭力梁悬架系统0～200 Hz频率范围内的低阶模态与车内“轰鸣声”密切相关，对整车NVH性能的不良影响尤为显著，因此将研究范畴定位于0～200Hz的低阶模态。

2 问题及研究步骤

图1为某车型扭力梁悬架系统。以0～200 Hz频率范围内的悬架结构约束模态频率分布作为描述悬架系统动态特性的重要参数，探究轮毂处边界约束强、弱对其的影响。

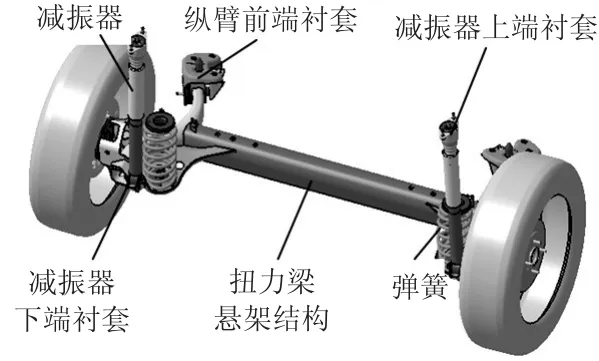
图1　某车型扭力梁悬架系统

具体研究步骤如下：

a.建立扭力梁悬架系统的有限元分析模型，计算钢制夹具（各向同性高刚度）约束轮毂状态下悬架系统的约束模态并将其与试验值对比以验证模型的置信度。

b.在模型中引入轮毂固定（刚性）约束、木块夹具（各向异性次高刚度）约束以及弹性衬套（低刚度）约束并利用Nastran软件计算3种约束状态下悬架系统模态振型和频率。

c.通过对比以上4种不同边界约束状态下悬架系统的约束模态频率分布和振型，分析轮毂处边界约束强、弱对扭力梁悬架系统动态特性的影响规律。

3 扭力梁悬架系统有限元建模及验证

3.1 模型参数获取

橡胶衬套动态特性受激振幅值和激振频率的影响［8～9］。当激励频率较高时，需要考虑衬套动态特性以使模型与实际情况较好地吻合。分别采用MTS831.50弹性体试验台和MTS832弹性体试验台测量橡胶衬套平动刚度和旋转刚度。由于Hypermesh软件中不能直接模拟橡胶衬套动刚度特性曲线，为考虑弹性元件动态特性对分析结果的影响，采用0～200 Hz频率范围内橡胶衬套动刚度RMS值来近似反映橡胶衬套的动态特性。表1给出了不同安装位置处衬套在0～200Hz频率范围内的动刚度RMS值。通过弹簧刚度特性试验台测试悬架弹簧刚度特性以及安装状态下的预压以便在模型中赋值，结果如表2所列。

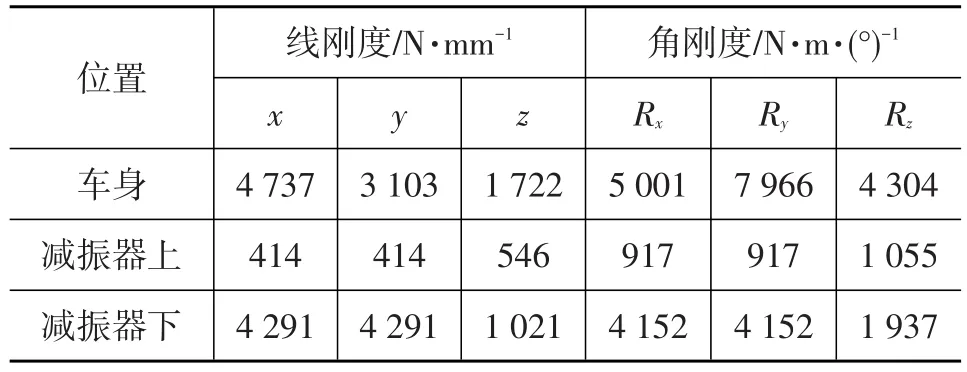
表1　橡胶衬套动刚度RMS值

表2　弹簧特性参数

3.2 悬架结构约束模态试验

拟通过悬架结构约束模态的仿真与试验分析结果对比来判断有限元模型的置信度。为此，首先需进行扭力梁悬架系统的约束模态试验。为排除轮胎的复杂影响以简化建模及验证，将拆掉轮胎后的轮毂直接固定在钢制夹具上。在上述约束条件下，采用LMSTest.Lab噪声与振动测试分析系统测试扭力梁悬架系统的约束模态（0～200Hz），结果如表3和图2所示。

表3　试验约束模态频率分布

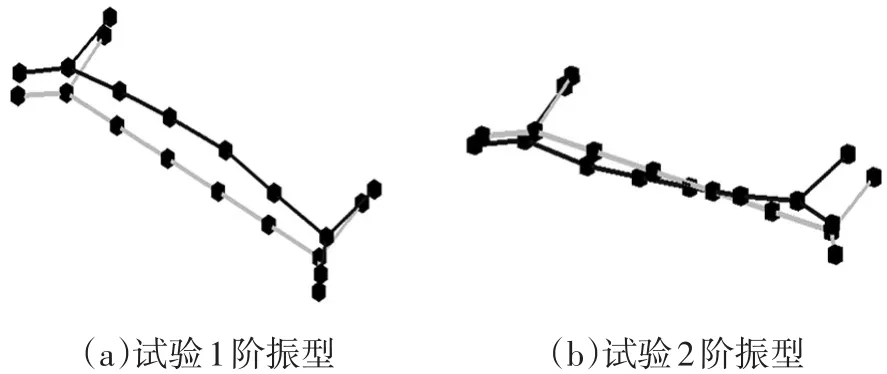
图2　扭力梁悬架结构约束模态试验振型

从表3和图2中可以看出，扭力梁悬架系统1阶约束模态振型是横梁进行上下弯曲振动，2阶约束模态振型是悬架从左侧到右侧进行波浪式振动。

3.3 模型建立与验证

采用Hypermesh软件对扭力梁悬架三维模型抽取中性面，用平面代替原CAD中的三维模型。对中性面划分网格并赋予45号钢材料属性及厚度参数，经多次调试对比后确定有限元网格类型为四边形或三角形壳单元，且网格尺寸为8mm，模型中共包含72 610个单元及80 882个节点，如图3所示。

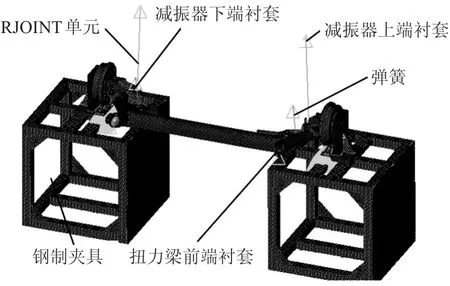
图3　带钢制夹具的扭力梁悬架系统有限元模型

通过CBUSH单元模拟悬架与车身、悬架与减振器以及减振器与车身的衬套连接，刚度值为对应的橡胶衬套动刚度RMS值（此处使用衬套在0～200 Hz频率范围内动刚度RMS值作为衬套刚度，以简化计算）；建立RJOINT单元模拟减振器工作缸和活塞杆的运动关系；建立钢制夹具模型约束轮毂。将模型提交Nastran2012软件计算约束模态并与试验值对比，如表4和图4所示。

表4　计算约束模态频率与试验值对比

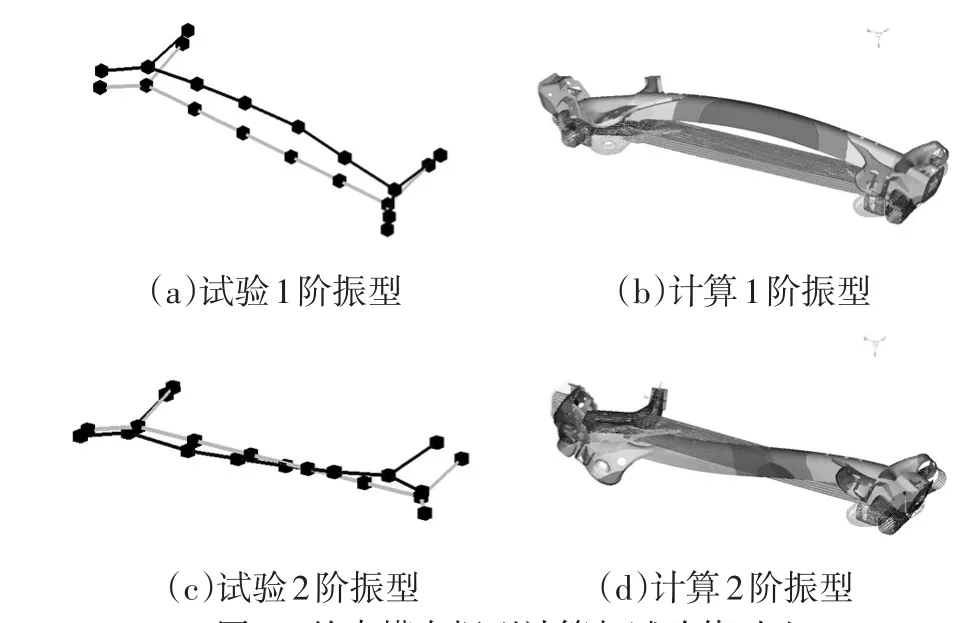
图4　约束模态振型计算与试验值对比

由表4和图4可见，计算与试验分析所得模态频率的误差在8.8%以内；且在所关心频带范围内出现的低阶（1阶与2阶）模态振型计算与试验分析结果也具有良好的一致性，说明模型精度能够满足后续分析研究的需要。

4 轮毂处约束强、弱对模态分布的影响规律

4.1 不同边界约束的设置与实现

为研究轮毂处约束强、弱对悬架系统低阶模态频率分布的影响规律，引入4种强、弱不同的约束：钢制夹具约束、轮毂固定约束、木块约束以及弹性衬套约束。前文已详细介绍对钢制夹具约束的处理，此处针对其余3种约束进行说明。

轮毂固定约束下悬架系统有限元模型如图5所示。轮毂固定约束是在模型中通过刚性单元将轮毂与大地建立固定连接，相比于钢制夹具，轮毂固定约束作用更强。第3种边界约束（图6）是在轮毂下方加入木块夹具代替夹具约束悬架，模型中木块与轮毂底部连接以模拟轮毂放置在木块上，木块下方与大地固定。相比刚性夹具，木块对轮毂的约束较弱。第4种边界约束是用弹性衬套约束轮毂即在模型中采用橡胶衬套将轮毂与大地建立连接，衬套刚度赋值为轮胎静刚度值以模拟轮胎在静平衡状态下的刚度特性。相比于木块夹具，橡胶衬套对轮毂的约束作用更弱，模型如图7所示。

图5　轮毂边界固定约束有限元模型

图6　轮毂边界木块约束有限元模型

图7　轮毂边界衬套约束有限元模型

4.2 影响规律分析

4种约束状态下的悬架结构有限元模态频率分析结果如表5所列，对应的模态振型如图8和图9所示。

表5　4种约束状态下计算约束模态

图8　4种约束状态下计算模态1阶振型

图9　4种约束状态下计算模态2阶振型

将不同约束状态下悬架系统同一振型对应的计算约束模态频率进行比较，如图10和图11所示。

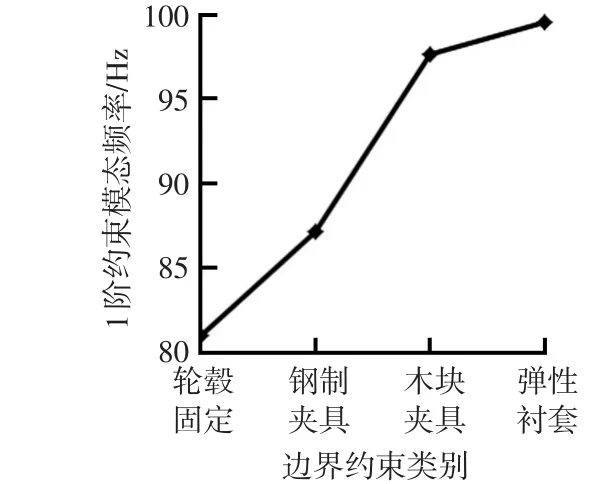
图10　1阶约束模态频率随约束强弱变化规律

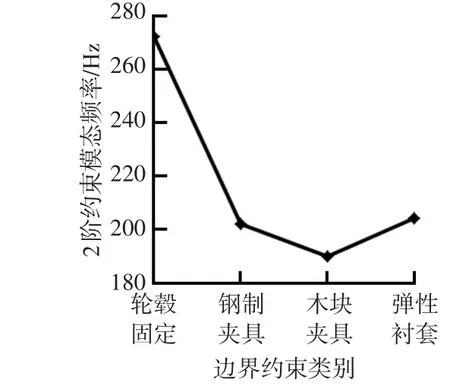
图11　2阶约束模态频率随约束强弱变化规律

由图10和图11可知，随着悬架轮毂处边界约束作用的减弱，其悬架1阶约束模态频率呈上升趋势，其中在轮毂固定及钢制夹具状态下，模态振动幅值最大位置为扭力梁中部，而在木块夹具及弹性衬套约束下，模态振动幅值最大位置位于制动鼓处；对于2阶约束模态，轮毂在固定约束状态下的悬架系统频率远高于夹具、木块以及衬套约束状态下的系统频率，并且当轮毂处约束作用逐渐变弱时，悬架系统2阶模态频率有所下降，但随着约束继续减弱，2阶模态频率又有增加的趋势。因此，可以通过调节悬架轮毂处边界约束强弱来改变悬架结构约束模态频率分布。

5 结束语

a.采用钢制夹具约束轮毂位置并考虑橡胶衬套动刚度特性后建立的有限元模型，其计算约束模态与试验约束模态的频率误差在8.8%以内，此约束状态下的模型精度较高。

b.轮毂处边界约束的强、弱对悬架结构模态具有“移频”效果，随着轮毂处边界约束作用由强变弱，悬架系统1阶模态频率不断增大，2阶模态频率不断减小。但随着边界约束作用继续减弱，悬架系统2阶模态频率有增加的趋势。

1陈无畏，李欣冉，陈晓新，等.车辆悬架中高频动态分析与橡胶衬套刚度优化.农业机械学报，2011，10：25～29.

2郝耀东.基于悬架系统的汽车NVH性能研究：［学位论文］.长沙：湖南大学，2013.

3陈晓新.基于刚柔耦合的整车动力学建模与悬架隔振性能分析：［学位论文］.合肥：合肥工业大学，2010.

4李欣冉，陈晓新，王家恩，等.橡胶衬套对汽车悬架系统NVH性能影响研究.合肥工业大学学报（自然科学版），2012（5）：581～584，643.

5李欣冉，陈无畏，陈晓新.基于刚柔耦合模型的悬架NVH性能研究.中国机械工程，2014（7）：978～983.

6何艳则.基于多体动力学的轿车扭转梁悬架运动学及NVH特性下的参数匹配优化研究：［学位论文］.合肥：合肥工业大学，2009.

7李欣冉，陈晓新，王家恩，等.橡胶衬套对汽车悬架系统NVH性能影响研究.合肥工业大学学报（自然科学版），2012（5）：581～584，643.

8陈茜.橡胶衬套动静态力学行为研究：［学位论文］.重庆：重庆理工大学，2014.

9杜艳霞，程建忠.一种基于参数化模型的弹性元件动刚度辨识方法.机械强度，2012（4）：495～499.

（责任编辑晨曦）

修改稿收到日期为2016年2月1日。

Effect Analysis ofW heel Hub Boundary Constraints on the Low-order M odal of Torsion Beam Suspension System

Gao Jidong，LiHongliang，Wang Haiyang
（China Automotive Technology&Research Center，Tianjin 300300）

【Abstract】With the rear torsion beam suspension system of a vehicle as research object，we use finite element method to research the influence law of strong and weak wheel hub boundary constraint on the low ordermodal frequency. We first establish the finite elementmodel of the suspension system constrained by steel clamp at the hub，calculating the constraintmodal and compare with the experimentalmodal analysis results，to verify the confidence level of themodel.On this basis，we analyze and compare the suspension system constraintmodal frequency distribution of the hub that uses fixed constraint，steel clamp constraint，wooden fixtures constraints and elastic sleeve constraint，the results show that when the wheel hub boundary constraint decreases，themodal frequency of suspension’s first-order constraint increases，whereas that of the second-order constraints decreases firstly，then increases.

Torsion beam suspension system，W heelhub boundary constraints，M odal

U463.21

A

1000-3703（2016）08-0027-04

天津市重点项目（14TXSYJC00457）资助。