先学后教，怎么学？怎么教？

江雄兵

【摘 要】这里所讲的先学后教有别于利用学习单开展的先学后教。以“比的化简”一课为例，呈现围绕教材展开的“先学后教”。教师在学生先学的基础上引导学生质疑，紧扣教材从学生不易思考的角度进行提问：“为什么教材要编排三道类似的例题？”“例题的每一步骤用等号连接的根据是什么？”通过两问既解决本节课重点，又为学生下次先学提供思路。

【关键词】先学后教 规则课 案例

学校举行深化课堂教学改革研讨活动，要笔者上一节体现“先学后教”理念的数学公开课。笔者以“比的化简”一课为例，围绕教学展开了“先学后教”的教学尝试。

一、课前慎思

（一）选课的烦恼

不同的数学课可能会用到不同的教学方法，同一种教学方法不一定适合所有的数学课。紧接教学进度的课有“起跑线”“比的认识”“比的化简”“复式条形统计图”等，这些课中既有概念课，又有综合实践课，还有规则课，哪一课更适合体现“先学后教”这种教学方法呢？最终，笔者决定选择“比的化简”这一节课当载体。因为“比的化简”是学生在学习了“商不变规律”与“分数基本性质”的基础上再学习的内容，这种学习属于规则教学的并列学习，根据六年级学生身心发展规律，他们完全能够把以前的学习经验、方法迁移过来。学生 “先学”会相对轻松。

（二）先学，怎么学

要设计一些导学案引导学生课前先学吗？课前的导学案会不会增加学生的学习负担？就让学生阅读教材的例题进行学习，可以吗？是课前先学还是课内统一学？怎样的“先学”能为后面的学习提供示范？……这些问题既有关于先学的时间问题，也有关于先学的方法问题，还有关于数学教学的责任问题。

经过思考，笔者有了自己的主意。如果教师设计了一些导学案给学生进行先学，哪会不会给学生一个暗示——没有教师下发的导学案，我是不太可能进行学习的？既然学生人手有一本教材，为什么不发挥教材本身的作用而要另起炉灶重新印制一些“导学”案？课外的自学，没有特定时间特定场合形成的“学习氛围”，先学的效果完全取决于学生的自我控制能力，这样做会不会导致学生的学习起点差异明显化，到时课堂交流时会不会影响参与度？……于是，笔者决定采用课内限时自学教材的教学方式。

（三）后教，怎么教

把学生当白纸去教，只要提笔就画，按构图一笔一画去涂抹，最后总能得到一幅作品。这是先教后学的好处，教师只要按照教材的设计去执行即可，借助一些教学资料，教什么还是比较好解决的。但是“先学后教”是在学生学习之后进行的教学，这时，白纸可能已经不再是白纸，有的可能已经有构图框架，有的可能已经涂上了颜色，教师要做的是怎样在这些基础上进一步完善，达到教学目标。先学后教，教什么是一大难题。

根据以前积累的教学经验，“比的化简”这一课，学生可能出现的困难如下：

1.从知识与技能上看：前项是后项的倍数时，学生可能会把结果写成一个整数，如60∶30=2；针对以往学生的知识掌握情况，学生在化简前项后项都是小数的比时可能会出现差错，如0.7∶0.35=7∶35；中下学生可能会混淆求比值与化简比。

2.从经验与思想方法上看：学生学习教材内容时很少会思考书本为什么会这么编写，很少会思考例题这样做的根据。

以上的预测都有可能成为课堂上教的重点。

几经思考，笔者把本节课的教学目标定位如下：

1.经历自学、交流、练习的学习方式，了解自学书本的方法。

2.理解化简比的根据，并能正确地化简比。

二、课堂实践

（一）明确任务自学书本

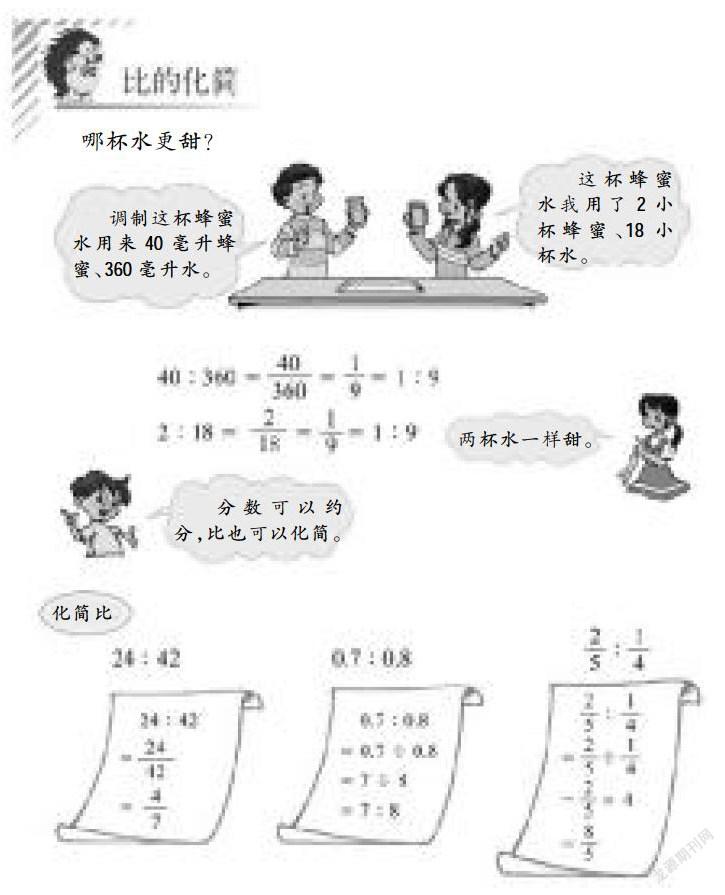
1.认识最简整数比。

凭感觉，从0.12∶0.4，∶，30∶60，1∶2中挑出最简整数比。排除的要说明理由。

2.揭题：今天，我们要学习怎样把一个复杂比化简成最简整数比。

3.出示自学要求：阅读教材第52页“试一试”前面的内容，学习怎样化简比。

教材图片：

4.初尝试。

化简下面各比。

30∶60 0.12∶0.4 ∶ 60∶30

学生独立练习，老师巡回指导，找出典型错例，让学生板书。

错例1：0.12∶0.4=12∶4=3

错例2：0.12∶0.4=1.2÷4=0.3∶1

错例3：60∶30=60÷30=2

（二）讨论交流

1.小组内交流4道尝试题。

2.对板书3个错题的讨论。

每道题找出错因，并进行订正。

3.师生质疑。

（1）师：学到这儿，同学们有什么疑问？

生：学习化简比有什么用？

生：为什么要学习化简比？

（2）师提问，引导学生深读课本。

①为什么书本上要讲三道例题？用其中一道例题不就可以讲明白了吗？

生：三个例题分别教我们怎样化简整数比、小数比和分数比。

教师引导学生看着例题用自己的话说一说，怎么化简整数比、小数比和分数比。

②例题的每一步为什么可以用等号连接，根据是什么？引导学生讨论化简比的每一步依据。

如：

0.7∶0.8

=0.7÷0.8→根据比与除法的关系，前项相当于被除数

=7÷8→根据商不变规律，被除数和除数同时扩大10倍，商不变

=7∶8→根据除法与比的关系，被除数相当于前项，除数相当于后项

（三）再尝试

1.化简比：3∶0.5 ∶ 168∶84

学生练习之后小组内交流、校对。班内交流时请有修改的同学说明错因及订正方法。

2.写出各杯子中糖与水的质量比。（单位：克）

（1）水：60 糖：30 （2）水：20 糖：10

（3）水：50 糖：10 （4）水：150 糖：30

这几杯糖水有一样甜的吗？

追问：你们是怎么判断出这几杯糖水一样甜的？继而解决学生在前面质疑环节提出的“学习化简比有什么用”的问题。

3.大正方形边长是4厘米，小正方形边长是3厘米。

大、小正方形边长的比是（ ），比值是（ ）。

大、小正方形周长的比是（ ），比值是（ ）。

大、小正方形面积的比是（ ），比值是（ ）。

讲评时，教师选了一份把比值写成比的作业进行展示，引导学生讲评，并体会求比值与化简比的异同。

三、课后研讨

（一）认可的做法

1.充分发挥教材的编写特色，引导学生体验“先学后教”。教师在质疑环节设计的两个问题既是对学生自学效果的检测，又是对学生自学方法的引领，还起到对本节课知识技能的“理”与“法”的梳理，可谓一箭三雕！

2.教师每次介入的时机把握恰当。

初尝试时，教师巡视收集学生中出现的典型错例，在学生小组交流后进行讨论，帮助学生弄清化简比的根据与方法。再尝试时，教师介入重点则放在学生还有修改的题上，真正做到学生已经知道的不讲、学生会的不讲。

（二）有争议的做法

在课后的讨论中，听课老师对以下两个问题表示有疑问：

1.先学后教能保证学习效果吗？

2.哪些课适合用这样的方法进行学习？

笔者的思考：

对于第一个问题，我在那节课的课后就作了一个后测。现将过程及结果描述一下。

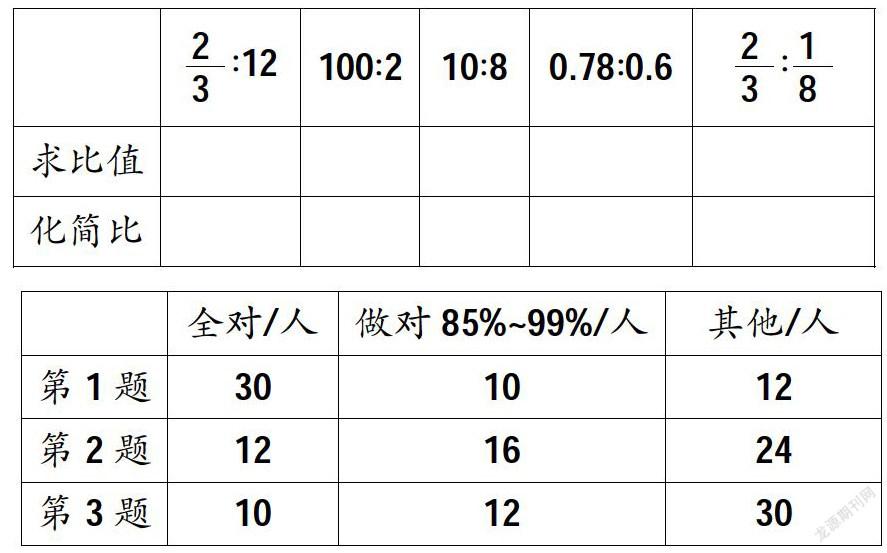
测试的内容：

1.化简比。

2.先求比值，再化简比。

3.小圆半径2厘米，大圆直径6厘米。

（1）小圆与大圆的半径比是（ ），比值是（ ）。

（2）小圆与大圆的直径比是（ ），比值是（ ）。

（3）小圆与大圆的周长比是（ ），比值是（ ）。

（4）小圆与大圆的面积比是（ ），比值是（ ）。

测试环境：

课内独立作业，完成就上交。

测试结果：

从数据分析及后续观察来看，这节课学生的学习效果还是不错的。其中第3题周长比与面积比约分不彻底的同学占多数。笔者把这类错误归因到解题技巧的缺失，在下一节课中补充。如小圆与大圆的周长比，学生算得小圆周长是12.56厘米，大圆的周长是18.84厘米，用12.56除以18.84求比值时找不到公因数314。而笔者是让学生不算出来直接用式子进行比、直接约分，即小圆周长：大圆周长=（3.14×4）∶（3.14×6）=4∶6=2∶3。

对于第二个问题。笔者认为，不同的课型，先学后教的策略可能不同。具体怎么做有待于实践当中继续研究。

经过这次实践，我们进一步理解了“先学后教”的含义。“先学后教”，先自学，后点拨。在学生自学课本、初步尝试、组内交流的基础上，教师根据学生的自学情况进行点拨，或规范其不准确的表达，或解答其疑惑的问题，或纠正其错误的理解，使学生成为教学活动的真正的“主体”。

（浙江省缙云县紫薇小学 321400）