分类法在初中物理教学中的应用

宋建辉

达尔文曾说过：最有价值的知识是关于方法的知识.物理课程标准也明确指出：“过程与方法”是课程目标之一，因此物理教学不仅传授基础知识和基本技能，更重要的是培养学生的科学思维方法，从而提高学生的思维能力和独立解决问题的能力，最终形成科学的素养.

分类法就是一种科学的思维方法，指的是解决某一问题时，由于存在不确定因素，难以统一解答，这时需要将可能出现的各种情况进行分类，然后逐一进行分析讨论，最后再对讨论到的各种情况的结果进行归纳整理，以得出问题的完整答案，即“化整为零，逐一击破，再积零为整”.分类法既是一种重要的逻辑方法，同时又是一种重要的解题策略.本文就分类法在初中物理教学中的应用，谈谈笔者的认识和看法.

1 在知识的形成过程中，领略分类法的魅力

分类法并不直接由物理知识、内容所表达，而是往往隐藏在知识之中，并支配着知识的获取及应用，因此在物理教学过程中，教师应充分挖掘教材中的方法论因素，让学生领会方法的内涵，领略方法的魅力.

例如，苏科版八下教材第九章力与运动，教材在探究力与运动的关系这一复杂问题时，分三个小问题加以讨论：（1）物体在平衡力作用下怎样运动？（2）物体在不受力作用下怎样运动？（3）物体在非平衡力作用下怎样运动？通过一系列实验观察，数据积累，进行整理和归纳，总结得出：（1）物体受力平衡时，将保持静止或匀速直线运动状态（即运动状态不改变）；（2）物体在没有受到力作用时，总保持静止或匀速直线运动状态，即牛顿第一定律；（3）物体在非平衡力作用下运动状态发生改变，可以概括得出结论：力是使物体运动状态改变的原因，力不是使物体运动的

原因.

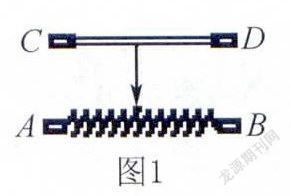
再如，苏科版九上教材14.4滑动变阻器，如图1所示，在让学生了解其机构、各部分的名称和铭牌上各参数的意义的基础上，为了探究其正确的接法，先让学生思考讨论如下问题：

（1）滑动变阻器共有A、B、C、D四个接线柱，如果只选其中的两个接入电路，可能有哪几种接法？

（2）如果将滑动变阻器A、D两个接线柱接入电路，向左移动滑片，滑动变阻器接入电路的电阻将怎样改变？电路中的电流将怎样改变？

学生讨论后得出：滑动变阻器任意两个接线柱接入电路可能有六种接法①A、D；②A、C；③B、D；④B、C；⑤A、B；⑥C、D.

接下来，学生设计实验、进行实验后得出：滑动变阻器能改变接入电路的电阻只有四种：①A、D；② A、C；③B、D；④B、C.进一步分析实验现象得出：①A、D与②A、C等效；③B、D与④B、C等效，最终概括为；滑动变阻器接线柱的正确接法是“一上一下”.

其实，教材中在很多地方都渗透着分类法的思想，这不仅体现人们对分类法思想的重视，让学生体验到分类法伴随在知识的形成过程中，更重要的是分类法思想能锻炼学生逻辑思维的条理性和严密性，增强逻辑思维的能力，提高分析问题和解决问题的能力.

2 在解题过程中，体验分类法的应用

2.1 对物体运动状态的分类讨论

一般情况下，由于所研究的问题中，运动物体所处的状态未知而使问题在求解过程中显得复杂，因此尽可能对物体所处运动的状态进行充分考虑，然后进行分类讨论.

例1 将一物块轻轻放入盛满水的溢水杯，物块静止后，溢出81 g的水；再将其轻轻放入盛满酒精的溢水杯中，有72 g的酒精溢出，则该物块的密度为

多少？

解析 此题属于浮力中较难的题目.首先根据阿基米德原理F浮=m排g， 可得 F浮水∶F浮酒=9∶8，求浮力不难，但难度在于确定物块静止时在液体中所处的状态，而此物块的状态具有不确定性，需分类讨论.可能有四种情形：

（1）物块在水、酒精中均漂浮；

（2）物块在水、酒精中均沉底（都浸没在其中）；

（3）物块在水中沉底，在酒精中漂浮；

（4）物块在酒精中沉底，在水中漂浮.

现将上述情形逐一分析：

（1）假设情形1成立，根据漂浮条件，受到的浮力等于自身重力，且物块的质量不变、重力不变，所以，物块在水中和酒精中受到的浮力相等，即

F浮水∶F浮酒=1∶1≠9∶8，与题意不符，所以假设情形1不正确.

（2）假设情形2成立，则物体浸没在水中和酒精中，物体排开液体的体积和自身的体积相等，

即V排=V物；又根据阿基米德原理F浮水=ρ水gV物，F浮酒=ρ酒gV物，得浮力比为F浮水∶F浮酒=5∶4≠9∶8，与题意不符，所以假设情形2也不正确.

（3）假设情形3成立，则违背物体的浮沉条件：漂浮ρ液>ρ物，沉底ρ物>ρ液，所以假设情形3不正确.

（4）因水的密度大于酒精的密度，

所以，由（1）（2）（3）可知，只能是物体在水中漂浮，在酒精中沉底（浸没），

根据漂浮条件，物体受到水的浮力F浮水=

ρ物Vg；

根据阿基米德原理，在酒精中受到的浮力F浮酒=ρ酒gV，所以，

F浮水F浮酒=ρ物Vgρ酒Vg=98

解得：ρ物=ρ酒=98×0.8g/cm3=0.9 g/cm3.

2.2 对物质的物理属性分类讨论

有些物理问题，由于物质本身属性变化，会使问题的结果出现多种可能，因此在解决此类问题时，需要对物理属性的多种可能进行分类讨论，才有利于问题的解决.

例2 现有A、B、C三个轻质小球，已知：A带正电，A和B相互排斥，B和C相互吸引，C和A相互吸引，则C带电情况的是

A.一定带正电 B.一定带负电

C.可能不带电 D.无法确定

解析 该题主要涉及A、B、C三小球中任意两球电荷间相互作用的关系.由于A带正电，B、C两球的电性未知，可能有多种变化，因而需对B、C两球的电性进行分类讨论，具体如下：

B球的电性可能有三种：

（1）若B不带电，则A、B相互吸引，

（2）若B带负电，则A、B相互吸引，

（3）若B带正电，则A、B相互排斥，

根据题意，可确定：B带正电.

接下来，判定C的电性，参照上述方法分析：

（1）若C带正电，则B、C相互排斥，

（2）若C带负电，则B、C相互吸引，

（3）若C不带电，则B、C相互吸引.

对照已知条件，C可能不带电、也可能带负电，故答案为：C.

2.3 对已知条件分类讨论

在某些物理问题中，由于已知条件不够明确，此时出现需要对已知条件的多种可能进行分类讨论，才能对问题进行求解.

例3 已知电源电压为6 V不变，现有两个定值电阻R1、R2接入电路中，串联在其中的电流表示数为0.25 A；若R1、R2换另一种方式接入电路中，电流表示数变为1 A，求R1、R2的阻值分别为多少？

解析 该题主要考查串、并联电路中电流、电压的特点和欧姆定律.解答此类题首先需要确定两个电阻的连接方式，但在已知条件中并没有明确表示，致使R1、R2的连接方式有几种可能：

（1）若R1、R2并联，则根据并联电路中电流、电压的特点和欧姆定律，可得

I=UR1+UR2

（2）若R1、R2串联，则根据串联电路中电阻的特点和欧姆定律，可得

I′=UR1+R2

比较上述两式，可得：I>I′，

由此可得 6VR1+R2=0.25A

6VR1+6VR2=1 A

由上述两式解得，R1=R2=12Ω.

综上所述，分类法在探究物理概念和规律以及解题过程中，应用非常广泛，所以教师在平时的教学中，要适时渗透物理分类法的思想，引导学生领会分类法的思想精髓，指导学生应用分类法解决物理问题，从而不断提高学生的思维能力和科学素质.