土地资源约束下的武汉城市圈经济增长实证研究

陈先强（1.湖北文理学院，湖北 襄阳 441053；2.华中科技大学，湖北 武汉430074）

土地资源约束下的武汉城市圈经济增长实证研究

陈先强1，2
（1.湖北文理学院，湖北 襄阳 441053；2.华中科技大学，湖北 武汉430074）

根据索罗增长模型的扩展，土地资源约束对经济增长的尾效随着资本产出弹性、土地产出弹性、以及劳动力增长率的增加而增加。以此为基础，从整体角度计算了武汉城市圈1995-2014年间土地资源对其经济增长的尾效，平均每年约为1.97%。从时间角度静态的分析了9个城市的土地尾效，发现不同的城市地区土地资源尾效差异较大。并从时间角度动态地分析了武汉城市圈整体土地资源尾效的变化，发现武汉城市圈土地资源尾效呈现先下降再上升的趋势。最后分析得出了土地产出弹性、资本产出弹性和劳动力增长率的变化是引起城市圈和不同城市土地资源尾效值变化的原因。

土地资源约束；武汉城市圈；经济增长；尾效；索罗增长模型

一、引言

土地是人类文明得以繁衍和发展的源泉，离开了土地，人类的一切文明成果将不复存在。随着我国经济的发展和城市化的高速推进，城市数量和城市规模不断的膨胀，特别是城市群落集团发展，使得城市稀缺的土地越来越成为阻碍城市经济增长的重要因素。自2007年武汉市城市圈获批为“全国资源节约型和环境友好型社会建设综合配套改革实验区”以来，武汉城市圈在经济高速增长的同时，城市基础设施建设的投资也在高速增长，城市外延不断扩张，城市用地越来越紧张，城市土地资源的约束越来越成为武汉城市圈经济增长的瓶颈。

自然资源作为资本要素，在经济增长过程中，资源的限制不可避免地会影响经济的增长。对于在资源约束下对经济增长的“阻力”分析，国内有些研究中用“尾效”来表示资源对经济增长的影响。薛俊波等［1］（p5-14）研究表明1978—2002年间，资源对中国经济的增长“尾效”为每年1.75%，是美国的7.29倍，如果继续在现行要素投入政策下，要实现2020年人均GDP比2000年翻两番，那么技术进步导致的经济增长率至少要达到0.6%。谢书玲等［2］（p22-25）认为在1983—2003年间，中国经济增长中水资源、土地资源的“尾效”分别为0.14%和1.32%，水土资源共同的“尾效”为1.45%，是美国的6倍。崔云［3］（p23）、杨杨等［4］（p34-38）分析了1978—2005年间中国经济增长中土地资源的“尾效”，前者采用K-D生产函数模型，得出平均每年约为1.26%，后者采用二级三要素CES生产函数模型，得出平均每年约为0.46%，两者相差较大。王家庭［5］（p2067）按中东西三个区域，分析了我国31个省区1997—2008年土地资源对区域经济增长的“尾效”，发现不同地区的土地资源“尾效”有较大差异，并随着时间的变化差异较大，人口增长率、土地产出弹性、资本产出弹性的提高是三个区域土地资源“尾效”存在较大差异的主要原因。金碚［6］（p31-80）分析表明在1981—2005年间，土地资源对我国的工业增长速度的“尾效”平均每年约为0.47%。

以上研究多从宏观层面来研究土地资源对中国或者区域经济增长的阻力效应，这样忽略了土地资源在不同的区域、经济发达地区和欠发达地区、人口数量分布的不同地区、农村和城市等稀缺性的差异。可以说在我国土地资源的稀缺性集中体现在城市密集地区，从土地资源对城市密集区经济增长影响的角度来研究，更能体现土地资源对经济增长的约束效应。我国是一个人口众多，土地稀缺的国度，是指可耕种、开发的土地少，人均占用量少，特别是在当前城市化高速推进的时期，大量人口、产业涌入城市，城市发展可开发利用的土地越来越稀缺，土地价格和地租越来越高昂，土地资源的限制越来越成为城市经济发展的瓶颈。因此，本文研究在土地资源约束下武汉城市圈经济增长，尤为显得有意义。

二、理论方法与模型

美国经济学家索罗［7］提出了索罗经济增长模型。基于索罗增长模型，加入土地这一变量进行扩展。那么生产函数可以表示为：

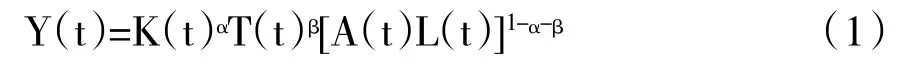
其中α＞0，β＞0，。表示产出，K（t）表示资本，A （t）表示技术进步，L（t）表示劳动，以及（t）表示土地。

假定资本、人口增长率和技术进步不变，其动态性与经典的索罗模型一致，即：

其中，s为储蓄率，δ为资本的折旧率，n和g分别为劳动和技术进步的增长率。由于在长期内，土地数量是固定的，受制于土地资源的有限性，用于生产的土地数量长期内不会增加，于是假设：

依据假定，A、L与T均以不变的速率增加。因此，在平衡增长路径上，资本和产出均以不变速率增长。那么，K的增长率为：

因此，在储蓄率和资本折旧率保持不变的情况下，要使K的增长率保持不变，Y/K就必然不变，则Y与K的增长率必然相等，即gY=gK。

对（2）式两边取对数，可得：

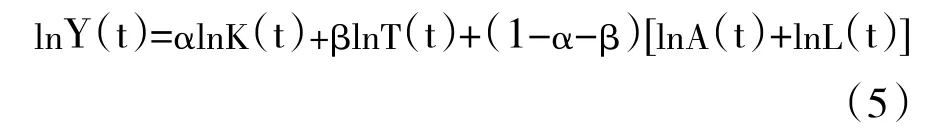
然后，对式（5）两边对时间求导，可以得到：

其中，gY（t）表示Y的增长率。A、L与T的增长率分别为g、n和0，因此，式（6）可以简化为：

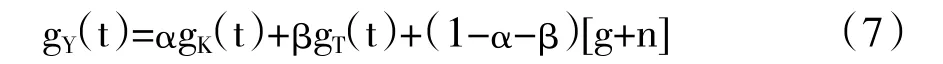
如果经济处在平衡增长路径上，把gY=gK代入式（7）可得：

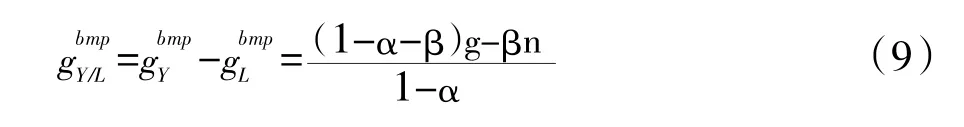
从式（9）可以看出，在资本增长率趋于均衡的情况下，单位劳动的平均产出可以为正，也可以为负。如果为负，则指生产活动由于受到土地资源的约束单位劳动平均产出下降，从而制约经济增长，但是不断的技术进步会推动经济增长。如果技术进步所带来的经济增长的动力大于土地资源约束对经济增长的阻力，那么经济依然可以持续的保持增长。

如果不考虑技术进步、资本投入对经济增长的推动作用，单从土地资源的约束对经济增长的限制来看，土地资源的约束在多大程度上会制约经济增长呢？本文可以利用不受土地资源约束和受土地资源约束两种状况下的平衡增长路径上的单位劳动平均产出的差额来表示土地资源约束下对经济增长的“阻力”，即土地尾效。

经济增长在不受土地资源约束的情况下，即在下的处于平衡增长路径上的单位劳动平均产出增长率为：

那么式（10）与式（9）的差额为在土地资源约束下就平衡增长路径上的单位劳动平均产出增长率的“阻力”，即：

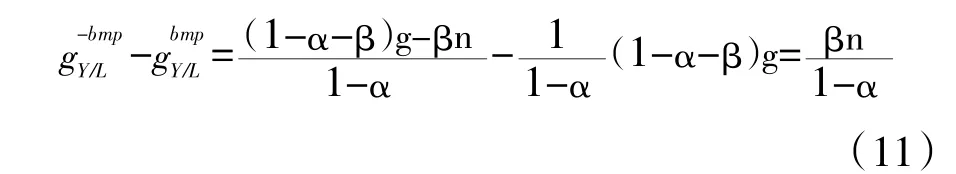
从上式可以看出，土地资源对经济增长的阻力随着资本产出弹性、土地产出弹性和劳动力增长率的增加而增加，这就要求要保持一个国家或者地区经济可持续增长，就不能过度的依赖资本、土地，不然，随着劳动人口增加，土地资源对经济增长的阻力就会越来越大。因此，要可持续的推动经济增长，降低经济增长的尾效的办法就是不断的推动技术进步。

三、实证分析

1.数据说明。

本文对武汉城市圈经济增长与土地约束进行实证分析，考虑到数据的可得性，选取1995—2014 年9个城市的有关数据。从以上的理论方法与模型分析来看，需要有关Y、K、L和T的数据，这些数据主要来自于《湖北省统计年鉴》（1996—2014）以及各个城市地区1996—2014年的统计年鉴，此外还参考了各城市地区2014年国民经济和社会发展统计公报。

（1）对于Y，本文选取的是1995—2014年武汉城市圈9个城市地区的GDP，并把当年价格计算的GDP转算成以1995年的不变价格计算的GDP序列。

（2）固定资本存量K，由于各统计年鉴中都没有直接的统计数据，需要对各城市地区的固定资本存量进行估算。关于资本存量的估计的相关研究有很多，本文采用常用的永续盘存法（Gold Smith［8］（p58-74））其基本公式为：

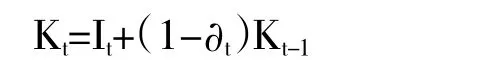
式中：Kt表示第t年的资本存量，It表示第t年的投资，∂t表示第t年的折旧率，Kt-1表示第t-1年的资本存量。根据公式需要知道投资序列It，按照数据的可得性，本文选取全社会固定资产投资指标，由于固定资产投资项目建设周期的不稳定性，当年的投资可能仅有部分转化成可投入生产的固定资产。本文假定1995—2014年武汉城市圈9个城市的全社会固定资产的平均建设周期为3年，且当年的投资仅有1/3转化成可投入生产的固定资产，那么第t年的新增固定资产为前三年的平均值，即：表示第t年的全社会固定资产实际投资。此外，还要根据各城市的固定资产投资价格指数把投资序列转化为以1995年为100的投资序列，由于在省际范围内，各地区固定资产投资价格指数差异不大，本文把湖北省的固定资产投资价格指数作为各城市的固定资产投资价格指数。对于固定资产折旧率∂t，同样的道理，本文把9个城市地区同一年的固定资产折旧率设定为相同的值，本文设定对全社会固定资产投资中的建筑安装工程、设备工器具购置、其他费用三类的折旧年限分别为40年、16年、16年，各类资产最后的残值率为5%，按几何效率递减模式折旧，最后以三类资产在总投资中的比重作为权重综合计算武汉市各年的总折旧率。对于初始资本存量K0，本文选用Reinsdorf和Cover［9］的方法来估算，初始0年的资本存量为当年的投资与之前各年投资在0年保存数量之和，即可以得到初始年份以前各年投资的无穷等比递减数列和：

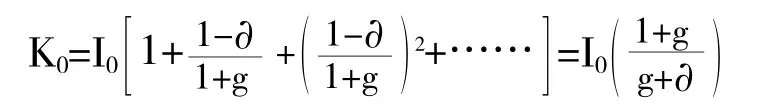
其中g为投资序列的平均增长率，∂为固定资产总折旧率。

（3）从业人员L，用各城市地区年末全社会从业人员数来表示。

（4）土地资源T，目前各统计年鉴对该指标统计非常不全面，由于城市和农村的土地资源使用功能不同，很难把城市和农村的土地用一个指标来表示，本文选取各城市地区农作物播种面积与城市建成区面积之和来表示土地资源投入。虽然这个指标没有包括所有被使用的土地资源类型，并与实际土地资源使用量存在一定的差距，但根据我国土地使用的比例来看，这个指标已经占到了所有土地使用量的75%以上。总的来说，虽然这个指标与实际的土地资源投入有些差异，但对测算土地资源对城市经济增长的约束影响不大。

2.数据的平稳性及协整检验。

由于在分析中的数据类型为时间序列数据，因此，需要对数据的平稳性、单整性进行检验，以免出现伪回归的现象。本文首先对9个城市地区的产出GDP、固定资本存量K、土地资源投入T和劳动力投入L四个数据的自然对数序列进行面板数据单位根检验，采用包括LLC、IPS、ADF、PP等方法检验，检验结果如下：

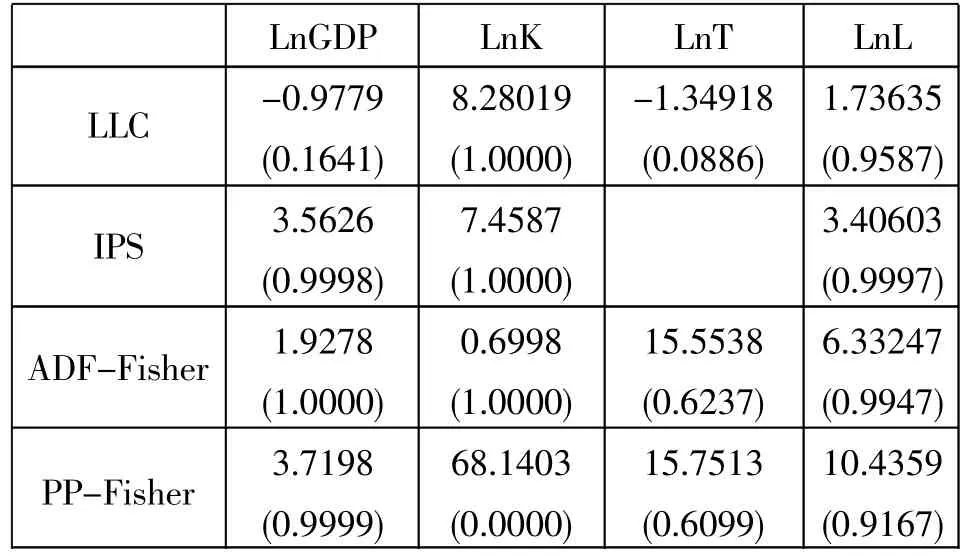
表1　武汉城市圈9个城市地区面板数据单位根检验（水平）

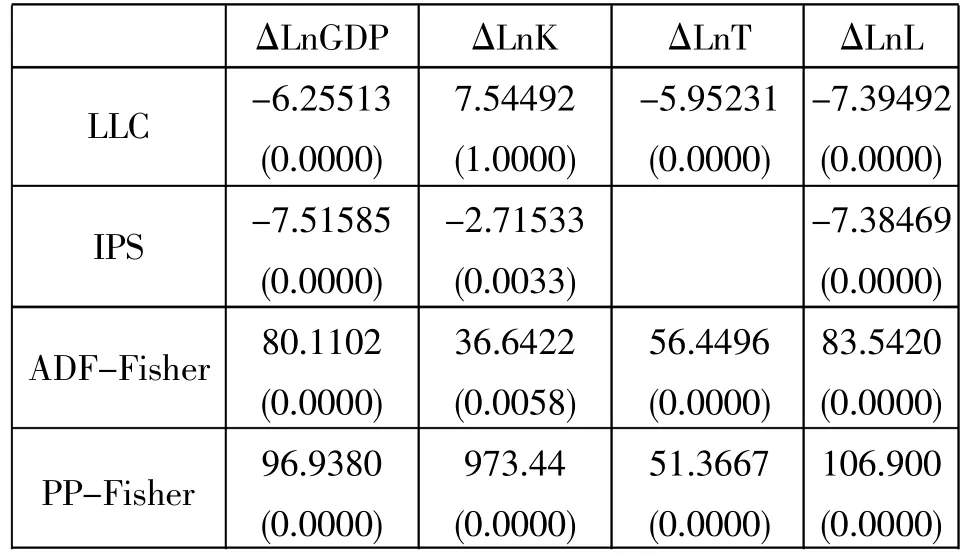
表2　武汉城市圈9个城市地区面板数据单位根检验（差分）

从表1的检验结果可以看出，LnGDP、LnT、LnL三个变量的四种单位根检验结果均在5%的显著性水平下不拒绝原假设，说明这三个变量存在单位根，是非平稳的。LnK除了PP-Fisher检验结果拒绝原假设，其他三种检验结果不拒绝原假设，按照少数服从多数的原则，说明LnK也是非平稳的。对各变量的一阶差分变量进行单位根检验，从表2的检验结果看，除了ΔLnK的LLC检验法不拒绝存在单位根的假设外，其他方法都拒绝单位根的假设，按照少数服从多数的原则，说明LnGDP、LnK、LnT、LnL是一阶差分平稳序列，即I（1）过程。如果LnGDP、LnK、LnT、LnL四个变量之间存在协整关系，才可以用它们来进行回归分析。

为检验四个变量之间是否存在长期稳定的关系，本文采用Engle和Granger二步法检验基础上的Pedroni协整检验法和Kao协整检验法。两种检验的原假设是变量之间不存在协整关系，Pedroni协整检验法主要看 Panel ADF-Statistic和 Group ADF-Statistic统计量的值，这两个统计量对检验协整关系是否成立最有效力。

表3　总样本的协整检验结果

从表3中的检验结果来看，三个统计量在5%的显著性水平下拒绝原假设，即变量系统存在协整关系，可以对其直接进行回归分析。

3.数据计量分析。

（1）城市圈视角下土地资源尾效测算结果静态分析。

在做面板数据回归分析时，模型选择上，我们经常用Hausman检验确定应该建立随机效应模型还是固定效应模型。

表4　模型选择的Hausman检验

根据表4的检验结果，Chi-Sq.Statistic统计量的P值小于0.05，拒绝个体效应与回归变量无关的假定，因此，应建立个体固定效应模型。根据式（5）进行回归，发现模型的残差存在序列相关性，因此，采用科克伦—奥科特迭代法来消除自相关性。最终得到的回归结果：

从回归的结果来看，资本、土地和劳动的产出弹性均为正值，并且都通过显著性水平为5%的T统计检验对产出有较为显著的影响。

从上述回归结果可知，α=0.4859，β=0.4772，由1995——2014年武汉城市圈总体从业人员数可以计算出城市圈总体劳动力增长率N，由公式：L1× （1+n）t=Lt

其中，L1表示计算初年的社会从业人员，即1995年，L1=1204.54万人，Lt表示计算末年的社会从业人员，即2014年，Lt=1832.23万人，t是计算的年数，t=20。据上公式计算的劳动力平均增长率n=2.12%。然后根据公式（11）计算得出土地资源对经济增长的“阻力”为0.0197，即在1995—2014年间，武汉城市圈由于土地资源的不断消耗，经济增长速度平均每年降低1.97%。

可以看出，武汉城市圈作为一个整体，是我国中部地区正在快速发展的城市群区域，在“1+8”城市圈中，经济发展水平武汉一头独大，其他8个城市的经济总量基本和武汉市持平，在武汉城市圈5.78万平方公里的国土面积中，可供利用的土地资源较多，但孝感、黄冈、咸宁等地级城市农业比重较高，需要占用的土地资源较多，因此，土地资源对整个城市圈经济增长的约束还是较为明显的。

（2）9个城市地区的土地资源尾效静态分析。

武汉城市圈9个城市不仅在土地资源拥有量上存在着较大的差异，经济发展水平上也存在着较大的不平衡，其主要表现在其他8个城市与武汉市的差距，因此土地资源对经济增长的约束在这9个城市地区也应该有差异。为了比较土地资源在武汉城市圈中对不同城市经济增长的影响，本文采用变系数面板模型，对武汉城市圈9个城市地区1995-2014年的数据进行分析，得到了各城市地区资本、土地产出弹性的估计情况。具体结果见表5。

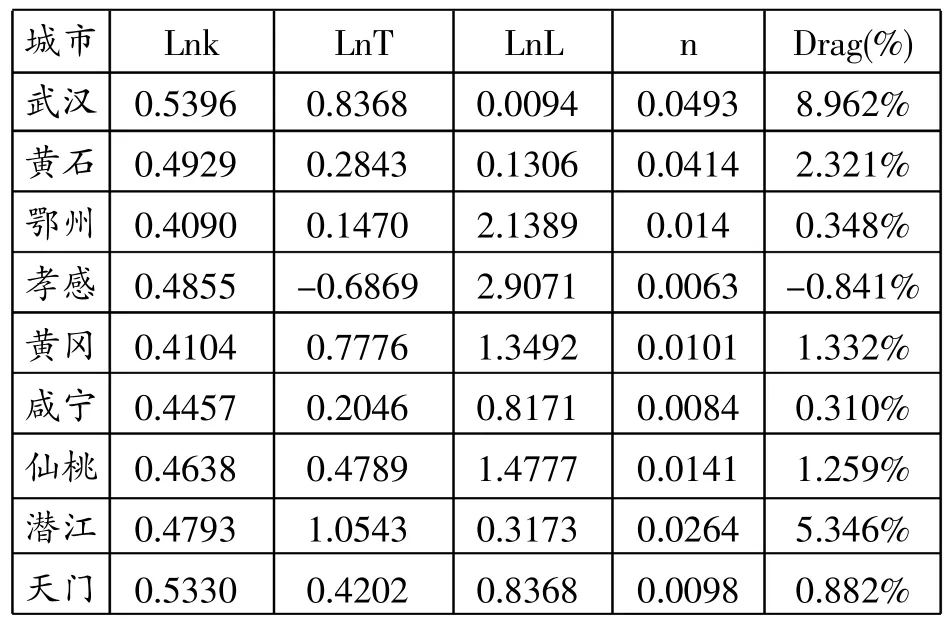
表5　武汉城市圈9个城市变异系数面板模型结果和土地尾效值

根据尾效值大小，武汉市、潜江市大于5，为强约束型，黄石大于1小于5为高约束型。这几个地区土地资源对经济增长约束较大，武汉市从2006年之后城市急剧扩张，土地资源变得紧张，土地资源产出弹性、劳动力增长率较高；黄石和潜江本身辖区土地面积在9个城市中较小，以发展重工业为主，劳动力增长率、土地产出弹性较高，因此，导致这三个城市地区土地资源尾效较高。黄冈、仙桃的尾效值在1到2之间，为中约束型，黄冈为农业和人口大市，但由于地处山区地带，经济发展落后，人均耕地并不多，土地产出弹性较高，但劳动增长率很低；仙桃市辖区面积较小，属于省直管的副地级市，农业比重较高，劳动力增长率较低，因此，导致这两个城市地区土地资源尾效较为适中。鄂州、咸宁、天门的土地资源尾效值在0到1之间，为低约束型，这三个城市地区辖区土地面积较小，劳动力增长率低，土地产出弹性也较低，因此，导致这三个地区土地资源尾效较低。值得注意的是孝感的土地资源尾效值为负，主要是因为孝感市的土地资源产出弹性为负，主要是因为孝感地区地处江汉平原地带，为农业大市，农业耕种面积较大，而农业的边际产出又较低，农业用地已趋近饱和。

（3）9个城市土地资源尾效动态分析。

城市圈经济增长是一个动态的过程，随着城市圈内土地资源开发和功能的改变，其对城市圈区域经济增长的影响也是一个动态的过程。为了更加全面地了解土地资源对区域经济增长的动态影响，本文进一步应用面板数据时间变动方法来分析经济增长过程中土地资源尾效的动态变化。

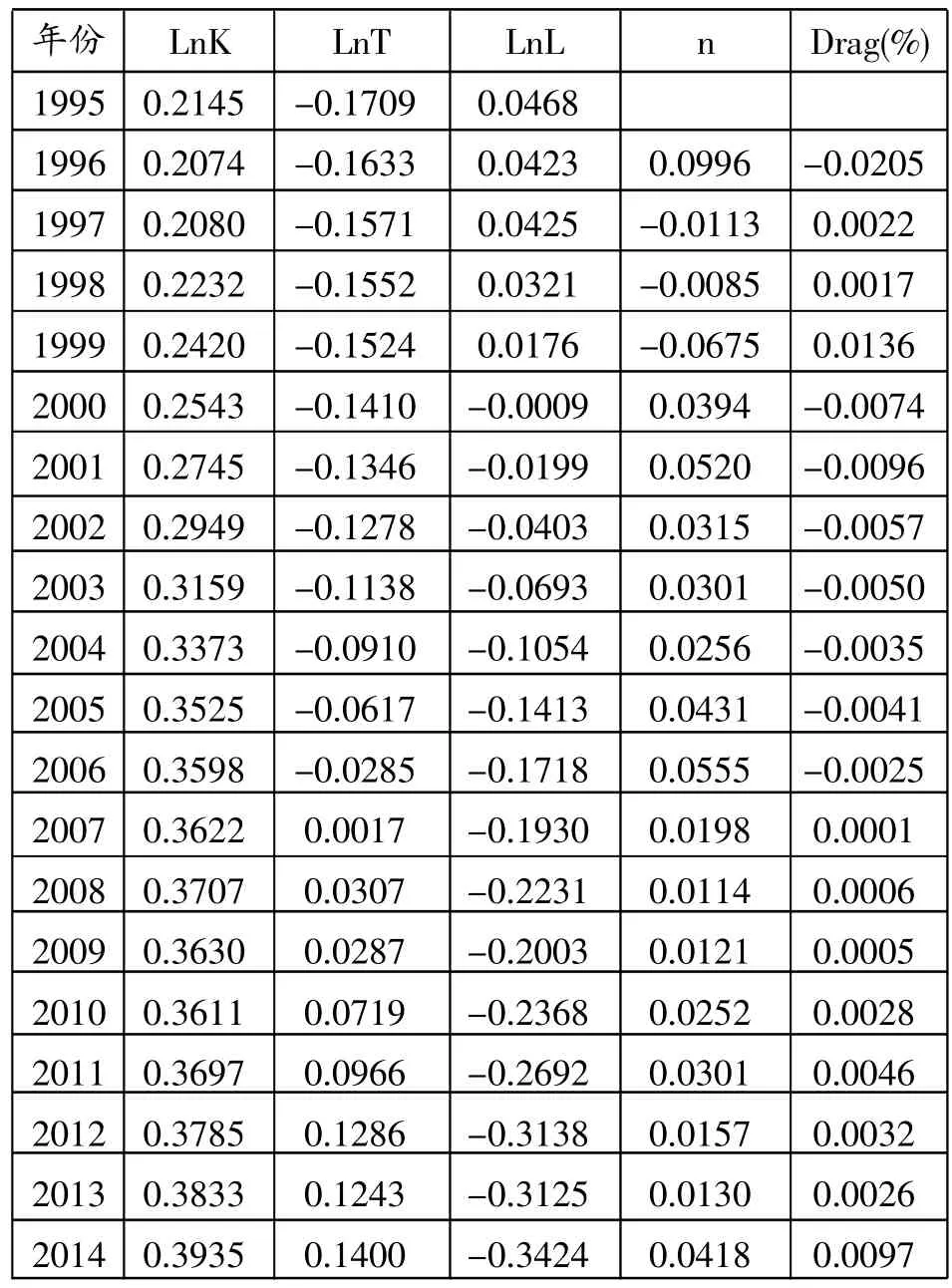
表6　1995—2015武汉城市圈经济增长中的土地资源尾效变化

从表6可以看出，武汉城市圈的土地资源尾效呈现出先上升后下降再上升的趋势，这主要体现在土地产出弹性和劳动力增长率的变化上，从1996—2006年间，武汉城市圈的土地产出弹性为负，但呈现不断的增大的趋势，这说明在此期间，土地资源的利用效率低下，土地资源投入对经济增长贡献小，土地的开发多用于效率低下的农业生产，或者土地的集约利用程度低；再者，结合劳动力增长率来看，工业化落后于城镇化，土地资源并没有成为制约武汉城市圈经济增长的因素。而在2007年，武汉城市圈正式获批为“资源节约型和环境友好型社会建设综合配套改革实验区”，城市化进程加速推进，土地资源的投入对经济的增长贡献越来越大，经济增长对土地资源依赖加大，从2007—2014年，武汉城市圈的土地资源尾效不断增大且为正，这主要体现在土地产出弹性的不断增大，各城市地区城市化速度加快，房地产行业高速增长，土地价格飞速高涨，土地财政严重，土地资源对经济增长的阻力也越来越大。

四、计量结果分析及讨论

本文分别从武汉城市圈的整体视角、9个城市土地资源尾效静态和整体动态分析土地资源约束对武汉城市圈的经济增长的影响。上述计量分析结果表明：

在1995—2014年间，武汉城市圈仅仅由于土地资源的不断消耗，经济增长速度平均每年降低1.97%。如果按照1.97%进行推算，到2030年，武汉城市圈经济增长率就会因为土地资源的约束而降低到2014年经济增长率的73%；到2040年，武汉城市圈经济增长率就会因为土地资源的约束而降低到2014年的60%。可见，土地资源对武汉城市圈经济增长将产生一定的制约作用。

从9个城市的土地尾效静态分析来看，武汉、黄石、潜江的土地资源尾效值较大，从回归结果来看，这三个城市地区土地资源弹性系数较大，资本产出弹性和劳动力增长率相比其他城市较高，表明这三个城市的经济增长依赖于土地资源的投入。特别是武汉市，在城市化快速推进的过程中，吸引了大量劳动力的流入，从业人员数量激增，导致对土地资源的需求大增，城市用地越来越紧张，土地资源的约束已在较大程度上制约着武汉市经济的可持续增长。

从武汉城市圈的土地尾效动态分析来看，土地产出弹性的大小和方向是影响土地资源尾效的一个至关重要的因素，从武汉城市圈1995—2014年的变化情况来看，土地资源尾效呈现不断增大的趋势，也就是说土地资源的约束对武汉城市圈经济增长的阻力越来越大。此外，从回归结果来看，资本产出弹性也呈现出缓慢递增的趋势，说明武汉城市圈经济增长在很大程度上还依赖于大量的固定资产投资，同时，土地的产出弹性也较为显著，也说明了武汉城市圈经济增长还依赖于土地资源的投入，近些年来武汉市基础设施大建设和城市边界不断地膨胀也印证了这一点。从式（11）可以看出，土地资源对经济增长的“阻力”越大，资源对经济增长的“阻力”就越大，要降低这个“阻力”，只能依靠降低资本、土地的产出弹性和降低劳动力增长率，即在武汉城市圈的经济增长过程中，不能过分地依赖资本、土地和劳动力增长。那么，要推动武汉城市圈经济可持续增长依靠什么呢？那就是知识创新、技术进步和制度创新，只有这样才能实现土地资源的可持续利用和城市经济的可持续增长。

［1］薛俊波，王铮，朱建武，吴兵.中国经济增长的“尾效”分析［J］.财经研究，2004，（9）.

［2］谢书玲，王铮，等.中国经济发展中水土资源的“增长尾效”分析［J］.管理世界，2005，（7）.

［3］崔云.中国经济增长中土地资源的“尾效”分析［J］.经济理论与经济管理，2007，（11）.

［4］杨杨，吴次芳，郑娟尔.土地资源约束对中国经济增长的影响［J］.技术经济，2007，（11）.

［5］王家庭.中国区域经济增长中的土地资源尾效研究［J］.经济地理，2010，（12）.

［6］金碚，等.资源与增长［M］.北京：经济管理出版社，2014.

［7］Romer，D.Advanced Macroeconomics［M］.Second edition，Shanghai University of Finance&Economics Press，The McGraw—Hill Companies，2001.

［8］Gldsmith R.W.，A Perpetual Inventory of National wealth，In Studies in Income and Wealth，ed.M. R.Gainsburgh，Princeton，1951.

［9］Marshall Reinsdorf，Mariam Cover，Measurement of Capital Stocks，Consumption of Fixed Capital，and Capital Services，Report on a Presentation to the Central American Ad Hoc Group on National Accou nts，May，2005.

责任编辑 周 刚

F127

A

1003-8477（2016）08-0063-06

陈先强（1978—），男，湖北文理学院经济与政法学院讲师，武汉大学经济学博士，华中科技大学访问学者。

湖北省教育厅人文社会科学研究项目“武汉城市圈资源与环境基础研究”（2012QX843）。