浅析动量流与电流相关性质的类比

皇甫泉生　吴国玢　顾铮（上海理工大学理学院，上海 200093）

浅析动量流与电流相关性质的类比

物理学的不同分支学科之间实际上存在着某些相似甚至相同的特征，因而可以进行类比.本文讨论力学和电学之间的类比.为此，首先以动量这一广延量作为力学的中心量，进而引入动量流的概念.文中在电荷量与动量、电流与动量流、电势差与速度差、电阻与动量阻、电容与动量容等各个相对应的物理量之间，以及相对应的计算关系式之间进行了类比，从而凸显出力学和电学的相似性或可比性以及宇宙事物的内在联系.不同分支学科之间的类比不仅可以拓宽师生的视野和思路，有利于物理教学，而且能提升人们对于力学，乃至整个物理学的认识水平.

类比；力学；电学；动量流；物质型物理量

类比方法在物理学的发展过程中经常起着启示、探索和创新的作用.卢瑟福根据α粒子散射实验得到的数据分析，将他想象中的原子内部的结构与太阳系的结构进行类比，建立起原子核结构的行星模型.类比有利于人们将新知识纳入到已有的知识系统中去，使相关知识能够融为一体，联结成一个有机的网络体系，产生举一反三、触类旁通的效果，因而被普遍应用于物理学理论的教学中.在力学中将刚体的定轴转动与质点的直线运动进行类比，使学生能较容易地掌握刚体定轴旋转运动的规律.类比在振动学中的应用亦相当广泛.在机械振动中，弹簧振子的运动方程，即振子相对于平衡位置的位移x随时间变化规律的数学形式可表示为：x=A cos（ωt+φ），而在LC回路中，电容器极板上电荷q随时间的变化规律则可表示为：q=Q cos（ωt+φ）.通过对比这两个方程，人们认识到LC回路中电荷量随时间的振荡规律十分类似于机械振动［1］.因此若把电路中电荷量以及电流、电场强度等物理量在某给定值附近随时间作周期性变化类比于机械振动，人们便可以从直观、形象的机械振动入手建立电磁振荡的概念.换言之，只要掌握了机械振动的规律，就能比较容易地弄明白电磁振荡的规律.毫无疑问，这些较为经典的类比在物理教学中一直发挥着有益的作用.

然而，由于上述类比中所选择的力学与电学对应物理量还不是最佳对应关系，致使力学与电学之间的类比囿于个例，被局限在较小的范围内.为了突破这种局限性，本文参照电学理论的结构，选择将动量这个广延量作为贯穿于力学的中心物理量，与电学中的电荷量这一广延量对应起来，并由此引入动量流的概念［2］.这样，力学与电学之间各主要物理量的对应关系就可以得到显著的改善.通过力学和电学中的动量与电荷量、动量流强度与电流强度、动量流密度与电流密度、速度与电势等相对应物理量及其计算关系式（即物理过程或现象中的规律）之间的类比，可以使这两门分支学科之间的相似性得以全面、清晰地显现出来，展露出一种全新的面貌.

1　电流与动量流

众所周知，电荷量（单位：库伦）是电学中的一个基本物理量.那么力学中有没有类似于电荷量的物理量呢？答案是肯定的，因为力学中的动量跟电荷一样，既是广延量又是守恒量.如有一个子弹射入一个静止的物体，那么子弹和物体的动量都会发生变化，并且子弹的动量减少多少，物体的动量就必定会增加多少.这一过程可以想象为动量从子弹流入了物体，即动量能够像电荷或液体和气体等物质一样不仅占据一定的空间体积，具有密度，而且还可以从一个空间区域流到另一个空间区域.德国卡尔斯鲁厄大学的G·Falk教授最早建议将电荷（量）、动量等广延量定义为物质型物理量（substance-like quantity）［3，4］，其目的是为了强调此类物理量能够像物质那样分布在空间并且在其间流动.

根据电流强度的定义：I=d q/d t；可以把动量在如固体材料、被拉伸的绳等能够传导动量的动量导体［5］内的流动看成动量流，而单位时间内流过任一截面的动量称为动量流强度（Ip），即：Ip= d p/d t.对照牛顿第二定律的数学表达式F=d p/d t，容易看出动量流强度正是大家所熟知的物理量力［6］.这意味着，凡是有作用力的地方就有动量流，凡是发生形变的地方就有动量流.

根据电荷守恒定律，在导体内任取一闭合曲面A，单位时间内经该曲面流入或流出的电量，必定等于该曲面所包围的空间区域V内的电量的增加量或减少量，即

上式就是电荷连续性方程的积分形式.若净流入（出）某区域的电量为零，则意味着该区域内的电量将保持不变.对于一个结点，如果不会有电荷的堆积或空缺，换言之，不会有电量的变化，故必然有∑I=0，即流入（出）一个结点的净电流必为零（基尔霍夫第一定律）.如前所述，将动量理解为物质型物理量意味着我们把它想象成一种“可流动的物质”，因而可以借鉴流体力学的方式来处理动量.在流体力学中，根据动量定理，分析流体质点系统与接触它的周界之间相互作用的关系可表达为［7］

其中，V代表所选择的控制区域；A代表该控制区域的表面积；p代表区域微元d V内流体的密度；u代表区域微元d V内流体的速度；∑F表示作用于该系统上的合外力.这样，其实就是在单位时间内整个控制区域内动量的增量；而

式（3）表明对于物体内所取任一闭合曲面A，单位时间内流入（出）该曲面的总动量，必定等于在同一时间内该曲面所包围的区域内动量的增加（减少）量，这就是动量连续性方程的积分形式.如果净流入（出）某区域的动量为零，则该区域内的动量将保持不变.对于一个静力学结构或结点，任何区域都不会有动量的变化，必然有：∑Ip=0，即流入一个静力学结构或结点的净动量流必为零.这类似于电学中的基尔霍夫第一定律.

为了说明前面公式中传导动量流和运流动量流之间的区别，可以将它们与电学做一个类比.人用力推小车前行时，人作为动量泵，从地面泵出动量，通过手将动量传递给小车，这里在人的手臂中流动的是动量，类似于导体中电流，因此在人的手臂中的动量流可称为传导动量流；而风吹帆船前行时，是空气把自身携带的动量传递给帆船而推动帆船前行的，类似于在显像管内运动的电子流，因此这种流动空气形成动量流就称为运流动量流.

2　动量在物体中的流动

把动量想象成像与电荷一样是可以流动的“流体”，那么动量在物体中又是怎样流的呢？如图1所示，设A板静止在光滑的平面上，让B物体在A板上运动，如果A与B的接触面存在摩擦，那么B物体的动量将会减少，A板的动量将会增加，直到两个物体的速度相同为止，且总动量保持不变.如果将其中的动量想象成如电荷一样可以流动，并且不生不灭，这自然就会认为动量是从运动速度大的B物体经接触面流入了运动速度小的A板，直到两者的速度相同为止，因此动量流动的驱动力为速度差.类似于两个不同电势的带电导体相接触，电荷会从高电势处流向低电势处，直到两带电导体的电势相同为止，电荷流动的驱动力为电势差.

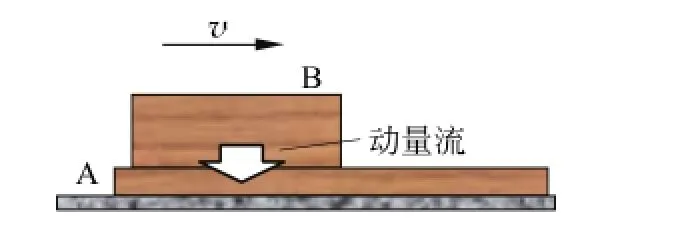
图1　摩擦时的动量流

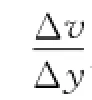
说明在此情形下，粘滞液体中的动量流强度与粘滞液体两端的速度差成正比，与粘滞液体的动量阻成反比，相当于在两个不同的电势之间接入了一个电阻，电阻中的电流遵循欧姆定律.

如果有两个同样的弹性球做对心碰撞，如图2所示.不妨设A球的动量为正，那么B球的动量为负，碰撞过程中A球的动量将由正值减少为零再减为负值，而B球的动量则从负值增加为零再增加为正值，而且总动量保持不变，这可以认为A球的动量通过接触面逐渐地流入了B球，直到两球都恢复原状，动量流才会停止.如果用一个弹簧将这A、B两球连接起来，既可以看到当弹簧被压缩时动量从A向B的流动，还可以看到当弹簧被拉伸时动量从B向A的流动［6］.就好像电学中的LC振荡电路，电荷会不停地在电路中来回振荡运动，电感在电路中起到了电泵的作用，弹簧则在动量流路中起到了动量泵的作用，利用自身的弹性形变产生动量流；而A、B两球犹如电路中的电容，在动量流路中储存和释放动量.而且从中可以得出以下结论：物体中动量流动的方向与动量正方向的设定和物体的形变（应力状况）密切相关，当物体无形变时，物体中的动量流为零；当物体被压缩（受压应力）时，动量流流向正方向；而当物体被拉伸（受张应力）时，动量流流向负方向［6］.由于动量流是矢量，当遇到不同方向的动量流时，需要把它们分解成二维甚至三维的分量来进行讨论.

假设固定在地面上的电动机（动量泵）拖拉着一物体，见图3，物体的速度为v，处于匀速运动状态.根据牛顿力学的观点，该系统在水平方向上至少有4个不同的力，其中一对是通过牵引绳作用在电动机与物体之间的拉力，一对是物体与地面之间存在着的滑动摩擦力，如图3所示.每一对力都遵循牛顿第三定律，而作用在物体上的拉力和摩擦力构成了一对平衡力，这4个力的大小都相等，因此物体匀速前进.如果设物体的运动方向为动量的正方向，那么上述事件可以描述为电动机（动量泵）从地面抽取动量，通过被拉伸的绳让动量流入物体，物体通过与地面之间的滑动摩擦（负载）把动量再传递回地面，这样动量“绕着一个回路”流动，如图4所示，回路中各处的动量流强度都相等，没有地方有动量的累积，因此物体水平方向的动量保持不变，物体匀速前进.这里水平方向的动量只有一个流回路，在其中流动的是动量，各处的动量流强度自然都相等.它等同于电学中的一个电源和一个电阻组成的简单电路，各点的电流强度都相等.如果关闭电动机，物体也停止了运动，假如此时牵引绳上还有拉力，那么物体与地面之间就会有静摩擦力，也就意味着尽管动量泵已经“罢工”，但回路中动量流依然存在，却没有能量的损耗，类似于电学中能量耗散为零的超导电流（electric super current），可称之为超导动量流（momentum super current）［8］.

除水平方向外，图4中的物体还有竖直方向的动量流.我们知道，地球附近的物体都受到地球的引力作用，因此物体与地球连线方向的引力场处于拉伸状态［5］，而物体与地面的接触部位则处于压缩状态，如果设向下为动量的正方向，那么竖直方向的动量从地球流出，经过引力场流入物体（动量流强度为mg），再从物体经接触面流回地球，构成一个竖直方向的动量流回路.如果物体处在空中，那么经过引力场流入物体的竖直方向的动量将累积在物体中，物体的动量会一直增加，物体将在竖直方向作匀加速运动.相当于处于均匀向下的电场中的正电荷，经过电场流入电荷的向下的动量（动量流强度为q E）将累积在电荷中，电荷的动量会一直增加，电荷将向下作匀加速运动.

图5是对载物桁架进行的动量流分析后所得到的水平方向动量流图［6］，不仅反映了动量的流动状况，而且尤如一幅光弹应力光图，一眼就可看出桁架的受力（动量流）情况.

图2　碰撞时的动量流

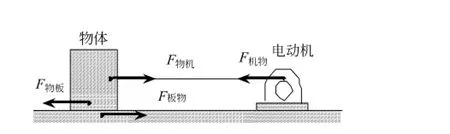
图3　电动机在地面上拉物体

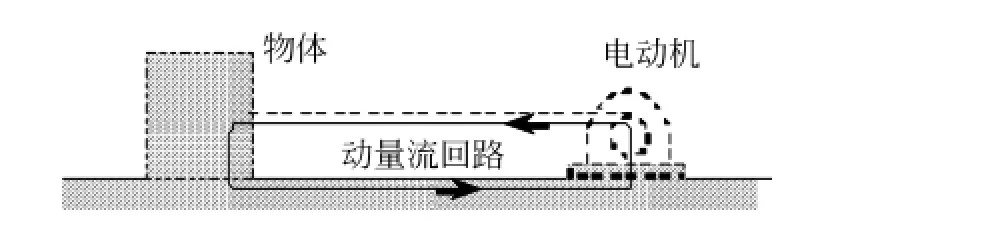
图4　动量“绕着回路”流动

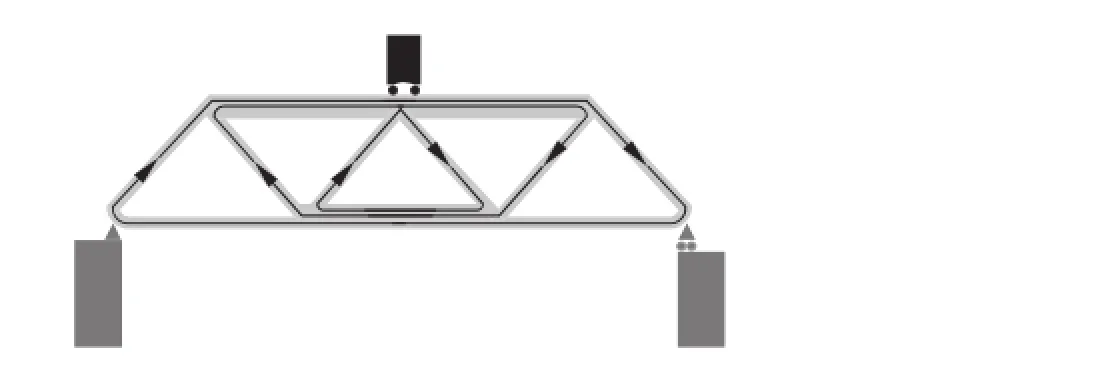
图5　水平方向的动量流图

导电材料根据传导能力可分为导体和绝缘体.类似地，传导动量的材料也可分为导体和绝缘体.动量的导体包括固体材料、拉伸的绳子、电磁场和引力场等.动量的绝缘体则包括轴承性能良好（能自由转动）的轮子和空气垫等.做气轨实验时，气轨上滑块的动量能保持很长时间不变，说明气垫有效地阻止了滑块的动量流失（流入地球），光滑的冰雪表面以及有良好轴承的轮子也会产生相同的效果.液体传导动量的能力介于固体和气体之间，一般会在不同程度上阻滞动量的传导，且其传导能力通常与温度有关（其粘度随温度而变：粘度越高，传导能力越强；粘度越低，传导能力越差），可以将液体视为动量的半导体.有趣的是，我们还能够在力学中找到与电学中的半导体二极管（单向导电）相对应的“力学二极管”（单向传导动量）：绳子——它只能在拉伸状态下（正向）传导动量却不能在压缩状态下（反向）传导动量.

3　一些力学与电学关系式的类比

电荷作为一种能量载体在流动时输送的能流强度（功率）为：P=U·I；动量作为能量载体，在流动时输送的能流强度（功率）为：P=v·Ip= v·F［6］.

电流超载会使导体过热，决定导线安全的因素是电流密度j（j=I/S）的大小.同样，动量流超载时也会引起动量导体的破坏，决定工程材料安全的因素是动量流密度σ（σ=F/S=Ip/S）的大小［9］.

电容器上增加的电荷与流入电荷前后的电势增量的关系为：Δq=CΔU.物体上所增加的动量与流入动量前后的速度增量的关系为：Δp=mΔv.可见物体的质量实际上还反映了物体储存动量能力的大小，所以质量可看作物体的动量容［8］（momentum capacity）.反过来类比，由于质量是物体运动惯性的量度，因而电容也可认为是电容器电势惯性（potential inertia）的量度［6］.

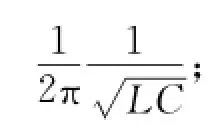
通过上述可以明显地看出，以动量为中心物理量来描述力学可以凸显出力学过程与电学过程之间的相似性，为二者之间的类比敞开了大门.运用类比，各个力学量和电学量一一对应起来，而且力学量之间的关系与相应的电学量之间的关系具有相同的数学表达式，从而反映出客观世界的统一和谐.当然，类比作为一种平行式思维的方法，并不是万能的，受到自然事物独特性的限制，力学与电学毕竟分属不同的学科分支，具有各自的特性，类比时要注意不同物理量之间的差别.比如，电学中的电势、电流是标量；然而力学中的速度、动量流却都是矢量，因此当遇到不同方向的动量流时，需要把它们分解成二维甚至三维的分量来进行讨论，需要有一定的空间想象能力.因此只有既掌握好不同学科之间的共性，又掌握好它们之间的个性，才能使我们对客观事物的认识更加全面深刻.

4　结语

将传统力学中的主要物理量力理解成动量流（强度）可以为人们提供一种研究力学的新方法.这种新方法不仅使力学自身的面貌一新，而且有助于在力学与电学（实际上还有其他分支学科）之间开展类比.将类比方法引入物理教学可以帮助师生从不同的视角去观察和认识我们周围的世界和宇宙，拓宽他们的视野和思路，激发他们的创新意识和创新能力.通过掌握这些新建立起来的概念、规律和方法，不仅有利于力学教学，还有利于人们在新的高度上重新认识整个物理学.

［1］ 程守洙，江之永.普通物理学［M］.6版.北京：高等教育出版社，2006.

［2］ 吴国玢.浅谈德国KPK物理教材的基本特点［J］.物理与工程，2010，20（5）：6-9.

［3］ Falk G.Was an der physik geht jeden an？［J］.Phys Blatter，1977（33）：616-620.

［4］ 吴国玢.关于德国KPK物理课程教学实验中若干问题的讨论［J］.物理与工程，2011，21（3）：43-45.

［5］ Herrmann F.德国卡尔斯鲁厄物理课程中文版力学［M］.戚华，改编.上海：上海教育出版社，2009.

［7］ 许贤良，王开松，孟利民.流体力学［M］.2版.北京：国防工业出版社，2011.

［8］ Herrmann F，Schmid G B.Analogy between mechanics and electricity［J］.Eur Phys，1985（6）：16-21.

［9］ 吴国玢.动量流强度和动量流密度及其破坏作用［J］.物理与工程，2012，22（1）：47-51，55.

A BRIEF DISCUSSION ON THE ANALOGY BETWEEN RELEVANT PROPERTIES OF MOMENTUM CURRENT AND THOSE OF ELECTRIC CURRENT

Huangfu Quansheng Wu Guobin Gu Zhengtian
（College of Science，University of Shanghai for Science and Technology，Shanghai 200093）

There exist some similar or even identical characteristics between the different branches of physics，which make the analogy between them possible.The analogy between mechanics and electricity is briefly discussed in this paper.Therefore，the concept of momentum current is introduced after the extensive quantity momentum has been taken as the central quantity in mechanics.Then，the analogies between such corresponding quantities in these two branches as electric charge and momentum，electric current and momentum current，potential difference and velocity difference，electric resistance and momentum resistance，electric capacity and momentum capacity，and the corresponding calculation formulas（relationships between the quantities）are simply conducted in the paper.As a result，the similarity or comparability between mechanics and electricity，and the internal connection of cosmic matters are highlighted.It is therefore anticipated that such analogies should not only be conducive to opening up new horizons for both teachers and students，activating their innovative ideas and hence promoting the teaching of physics，but also be beneficial for improving people，s cognitive level of mechanics and even whole physics itself.

analogy；mechanics；electricity；momentum current；substance-like quantities

2015-10-10；

2015-12-03

2016年度教师教学发展研究项目（CFTD1605DY）；上海理工大学“精品本科”系列教材——《大学物理基础》项目支持（编号2015-JPBKJ-018）.

皇甫泉生，男，讲师，主要从事大学物理教学科研工作. hufken@163.com