基于三阶累积量一维切片的微地震信号时延估计*

陈祖斌,刘　昕,孙　锋†，吕　昊，王东鹤

(1.吉林大学 仪器科学与电气工程学院，吉林 长春　130061；2.吉林大学 地球信息探测仪器教育部重点实验室，吉林 长春　130061)



基于三阶累积量一维切片的微地震信号时延估计*

陈祖斌1,2,刘昕1,孙锋1,2†，吕昊1，王东鹤1

(1.吉林大学 仪器科学与电气工程学院，吉林 长春130061；2.吉林大学 地球信息探测仪器教育部重点实验室，吉林 长春130061)

由于微地震有效信号易受环境噪声的干扰，严重影响时延估计值获取的准确性.基于此，提出了基于三阶累积量一维切片的方法进行微地震信号时延估计.首先计算信号的三阶自累积量和互累积量，为减少运算量满足野外实时要求取其一维切片，最终通过准则函数求取时延值.相对于传统的互相关方法，该方法对相关性未知的高斯噪声具有不敏感的特点，对相关高斯噪声有更强的抑制能力.仿真结果表明，在添加信噪比为-5～15 dB的随机高斯噪声和相关高斯噪声时，其时延检测概率和均方根误差优于互相关方法.在实际资料应用中，对实际微地震噪声进行了概率分布统计分析，并且基于井地联合监测方式，选取井中信号作为参考道对地面资料进行时延值的求取.仿真和实际资料处理验证了该方法的有效性和实用性.

参数估计；噪声抑制；三阶累积量；微地震监测；一维切片

微地震监测技术是一门交叉学科的新技术，它是通过观测、分析生产活动中所产生的微小地震事件来监测生产活动中产生的影响、效果及地下状态的地球物理技术[1].微地震监测技术在油田水力压裂监测、煤层气压裂监测、矿山与地质灾害监测等领域发挥着越来越重要的作用[2-4].微地震监测分为井中监测和地面监测，地面监测受到的环境干扰很大，相比于地面监测方式井中监测获得的微地震信号信噪比要高，基于井中-地面联合监测的方式近些年来得到广泛应用[5-6].

与常规地震勘探信号相比，微地震信号十分微弱，震级大约在-3级到+1级，有效地压制噪声获得时延估计值对后续的微地震信号识别和震源定位等工作至关重要.Eisner等[7-8]提出了一种基于“主事件”(信号明显)与“从事件”(信号不明显)互相关运算的方法来压制噪声并进行震源定位.但是，相关运算的前提是噪声与噪声之间是不相关的，而实际的微地震资料中噪声的相关性未知，且可能具有很强的相关性，这样，相关方法获得的时延估计值是不准确的.

随着高阶统计量理论的逐步完善，由于高阶累积量对高斯噪声不敏感等特性，在地球物理领域尤其在地震信号方面获得了成功的应用[9-10].冯智慧等[11]将四阶累积量应用到地震信号初至拾取中，拾取精度不亚于人工方法，并且效率大大提高；熊晓军等[12]将高阶统计量应用在油气检测中；唐斌等[13]在地震子波恢复也获得了成功应用；宋维琪等[14]研究了基于贝叶斯框架的四阶累积量的自适应算法能够有效地提取出微地震的有效信号.

本文基于微地震井中—地面联合监测方式，以井中信号为参考道，可以降低时延估计过程中的累积误差；运用三阶累积量一维切片对微地震信号进行时延估计，能够降低其估计方差，减少运算量，并且能够有效压制微地震高斯噪声，且获得准确的时延值.理论模型证明了该方法的可行性并且优于互相关方法，实际资料也获得了较好的应用.

1　基于互相关的时延估计方法

在地球物理学中，时延估计是一个重要问题，即需要确定两个传感器接收信号的时间延迟或者接收信号相对于发射信号的时间延迟.最常用的方法是(广义)互相关方法.

假设x(n)和y(n)是空间分离传感器观测结果，满足方程[15]：

(1)

式中：s(n)为有用信号；s(n-D)为s(n)的时延信号；λ为振幅因子；w1(n)和w2(n)为两个传感器的观测噪声，它们相互独立并且与信号s(n)不相关.

在信号处理中，两路信号的相似性等价于求它们的互相关函数.因此，x(n)和y(n)的互相关函数为：

(2)

式中：Rss(τ)为有用信号的自相关函数.

由于Rss(τ)

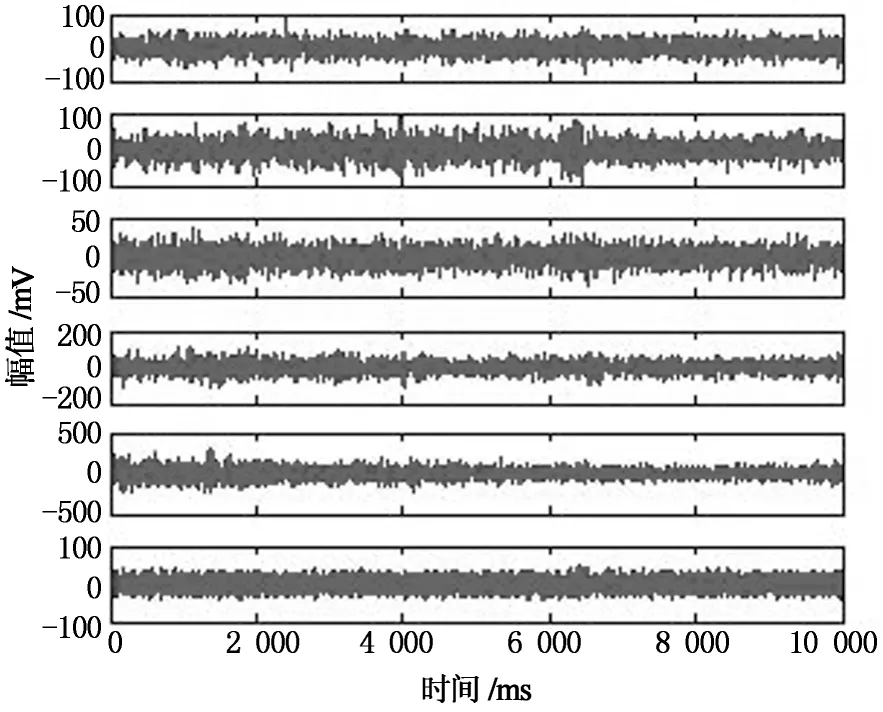
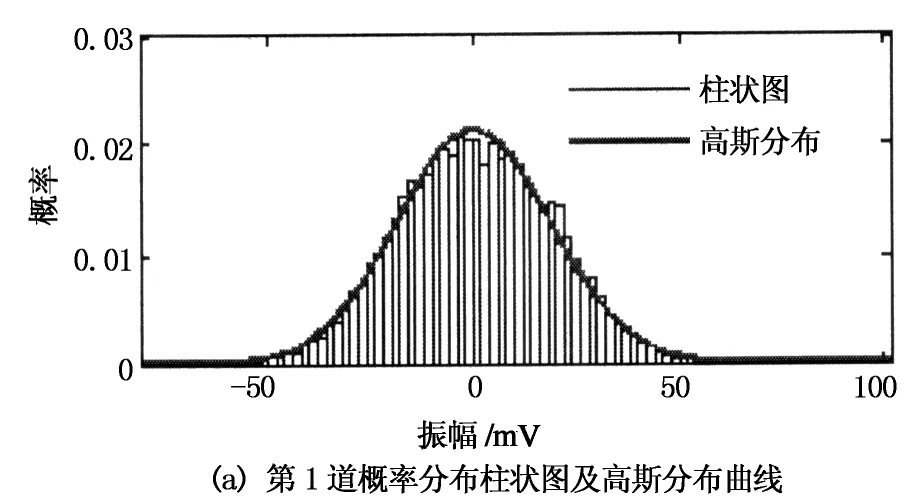
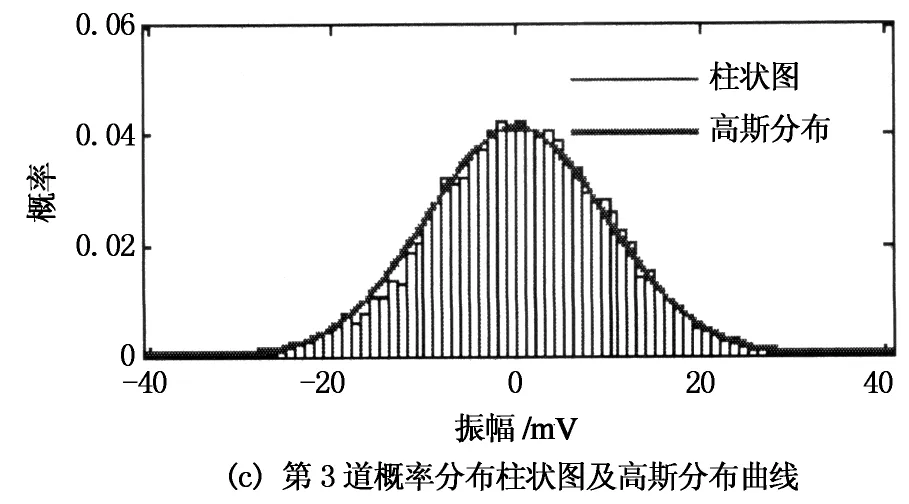
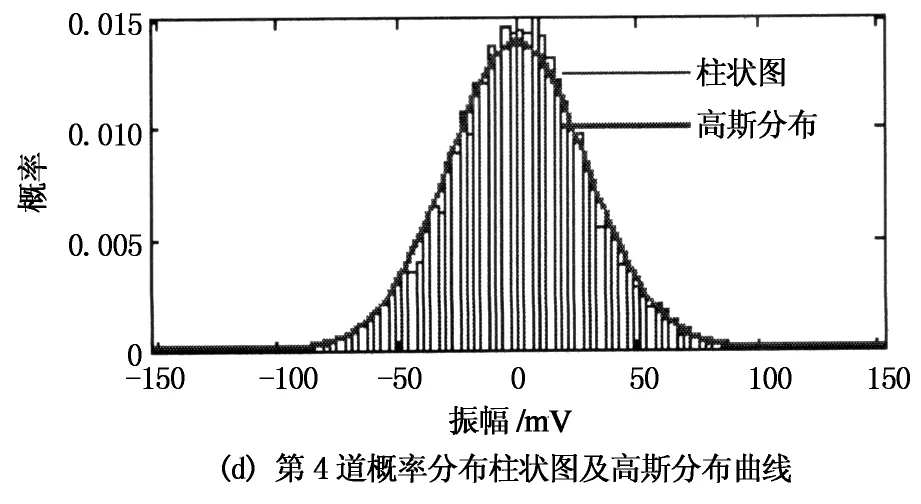
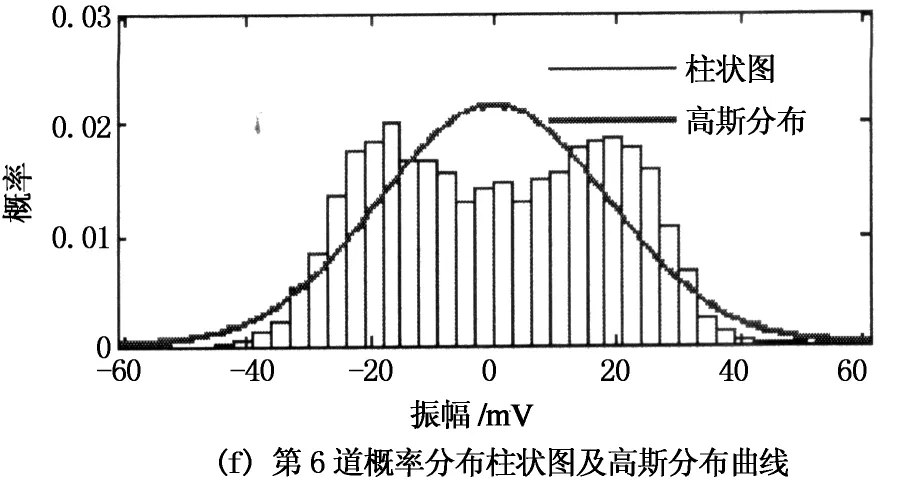
2　基于高阶累积量的时延估计方法

2.1高阶累积量的定义及性质

随机变量的概率密度函数可以描述随机变量的概率特征，概率密度函数的傅里叶变换称为特征函数φ(ω)，特征函数的对数函数称为第二特征函数ψ(ω).随机变量x的高阶累积量定义[16]为：

(3)

(4)

目前高阶累积量常用的是三阶和四阶累积量，二阶累积量常常等价于相关方法，而四阶累积量运算难以满足野外现场实时处理的需求，因此本文采用三阶累积量进行运算.高阶累积量运算通常是在零均值平稳随机过程前提下进行的，其三阶自累积量和三阶互累积量分别为：

(5)

高阶累积量中常用的两个性质：

1)高斯随机过程的高阶累积量恒为零，那么一个非高斯信号是在与之独立的高斯噪声中被观测的话，其观测过程的高阶累积量等于非高斯信号的高阶累积量[16].

2)如果3个随机变量x1，x2，x3中有一个变量和另外两个变量相互独立，则其三阶互累积量为零[17].

2.2基于三阶累积量一维切片的时延估计方法

微地震资料应用高阶累积量进行数据处理时应满足公式(1)中有效微地震信号为零均值、非高斯分布.公式(1)中的噪声为零均值加性高斯噪声，并且与信号独立，噪声之间可以是相关的，也可以是不相关的.非零均值可以通过减去均值估计变成零均值.微地震信号(无源信号)震源机制复杂，可视为非高斯信号[18].

对式(1)中的x(n)和y(n)求三阶互累积量和x(n)的三阶自累积量分别为：

(6)

由前面提到的两个性质化简可得：

(7)

由式(7)可以看出，三阶累积量中的第2个参数τ2不含有延迟量D的信息，所以为了减少计算量，实际应用中取其三阶累积量一维切片，优化处理后不仅有利于图形显示，还降低了估计方差.最终结果仍然包含微地震信号高阶累积量信息和时间延迟D，并且零均值高斯噪声的高阶累积量一维切片值依然为零[19].形成的三阶累积量一维切片定义为两个新的信号：

cxyx(τ,0)=csss(τ-D,0)；

(8)

cxxx(τ,0)=csss(τ,0).

(9)

其准则函数为：

(10)

由

可以看出，0≤J(d)≤1，当d=D时，J(d)取最大值.因此，可以利用三阶累积量一维切片定义的准则函数来求取时延估计值.

2.3参考道的选取

参考道的选取一般有3种途径：1)选取固定的一道作为参考道，然后进行高阶累积量的时延估计运算；2)每次都选取前一道作为参考道，然后运用高阶累积量对相邻道进行时延估计运算；3)把相似道先进行分组，再进行高阶累积量时延估计运算[11].

实际的微地震信号很微弱，信噪比低，尤其是地面微地震资料.相对于地面微地震资料，井中资料的信噪比较高，容易识别出有效信号.基于此，采用了基于井中-地面联合微地震监测方式，以井中资料作为参考道，对地面微地震资料进行时延估计，压制高斯噪声，获得了更准确的时延值.

2.4基于三阶累积量一维切片方法的微地震信号时延估计步骤

1)首先截取井中与地面相同时间段和相同时窗长度的数据，其中包含微地震有效信号.这样既可以减少计算量，也避免了无效微震信号噪声的干扰.

2)对截取的数据段进行归一化、去均值、带通滤波等预处理，使其满足高阶累积量运算假设.

3)以井中数据作为参考道，运用上述方法与地面各道信号进行时延估计运算，将得到的值保存.

4)得到的时差值可用于接下来的初至拾取和震源定位处理中.

3　微地震资料噪声分析

微地震监测环境噪声复杂，产生的干扰波可能与微地震传播机理和环境等因素有关.总体可以分为相干噪声和随机噪声.在理想情况下，无限范围的地震噪声根据中心极限定理总体呈现高斯分布[20].为了适用于本文所提方法，首先分析了实际噪声的概率分布情况.图1为2014年在山西进行煤层气压裂监测压裂结束后采集的噪声干扰，截取其一段数据中6道噪声数据进行概率分布分析得到图2(柱状图为实际噪声的概率分布).

图1　6道噪声数据

图2　6道噪声数据概率分布柱状图及高斯分布曲线

由图2可以看出，有限数据的噪声概率密度分布大部分图2(a)-图2(e)呈“钟形”，基本满足高斯分布特征.图2(e)由于大振幅短时瞬态信号的存在，出现了一个峰度值.图2(f)出现了双峰度，这是由于现场存在大振幅的周期性噪声信号.从对噪声的概率统计特性分析可以得出：当噪声中存在一些窄带强噪声或大振幅的周期性噪声时呈现非高斯分布，与猝发性环境有关，主要是野外施工中机械振动和人为振动产生的干扰，它是少样本随机分布的；而高斯噪声是在全范围内存在的，具有持久保持性.因此，实际监测现场环境噪声信号的分析结果表明该应用场合满足本文所述方法所需的理论基础.

4　仿真实验

仿真中采用地震勘探领域常用的Ricker子波模拟有效信号，将其合成微地震记录来验证提出算法的可靠性.Ricker子波的主频设为50Hz，合成记录道集为30道，每道间的时间延迟为10ms，如图3(a)所示.为了验证基于三阶累积量一维切片的方法在去除高斯噪声方面优于相关方法，分别在原始记录上添加随机高斯噪声和相关高斯噪声，分别如图3(b)和图3(c)所示.可以看出，相关噪声产生了一些假同相轴.

以第1道为参考道，用后续的道与参考道进行本文方法的时延估计运算.选取第2道为例与参考道进行运算，其理论时延值为10ms.图4为分别添加随机噪声和相关噪声的情况下，本文方法和传统互相关方法通过1 000次Monte-Carlo实验获得的不同信噪比下的时延检测概率.由图4可知，无论是在随机噪声还是相关噪声的影响下，本文方法都优于互相关方法，尤其在相关噪声干扰下，互相关方法在低于0dB是基本失效.图5为分别添加随机噪声和相关噪声情况下，本文方法和传统互相关方法通过1 000次Monte-Carlo实验获得的不同信噪比下的均方根误差.由图5可知，本文方法均方根误差值小于互相关方法结果，同样通过定量分析证明了本文方法的优势.图6为含有相关噪声的数据在信噪比为-3dB时运用互相关方法和本文方法进行的一次时延估计结果.由图6中圆圈处可知，基于互相关方法的最大值的时延值在零点左侧，这是相关噪声的影响，干扰了实际时延值的拾取，而基于三阶累积量一维切片方法可以正确计算出时延值，受相关高斯噪声影响很小，并且三阶累积量一维切片方法获得的结果的旁瓣要比互相关方法小，提高了检测分辨率.在实际资料处理中，信噪比极低的情况下也要对资料进行滤波等预处理，尽量提高信噪比.

图3　合成微地震原始数据及含噪数据

图4　不同信噪比下的时延检测概率(1 000次Monte-Carlo实验运行结果)

图5　不同信噪比下的均方根误差(1 000次Monte-Carlo实验运行结果)

图6　传统互相关方法和本文方法运行一次的时延估计对比(相关噪声SNR=-3 dB)

5　实际资料处理

资料处理采用2014年在山西某地进行煤层气压裂监测的实际数据，仪器系统均为本单位自主研发，其中，井中监测采用五支高精度三分量采集短节，地面采集利用无缆遥测地震仪，外接与井中匹配的高精度三分量检波器.截取了相同时间段的井中和地面数据，图7(a)为井中采集的五级三分量原始数据，信噪比较高；图7(b)为16个地面采集站的原始数据，明显看出其受到了严重的噪声干扰.应用上述方法，选取井中第2道Y分量的数据和地面的第2道Y分量数据，分别对其进行去均值、归一化、带通滤波等预处理，结果如图8(a)和8(b)所示.运用本文提出的三阶累积量一维切片方法对井中和地面数据进行时延估计，所得结果如图8(c)所示.从图中可以看出三阶累积量一维切片方法能够相对准确地求取出时延估计值.图8(d)为运用互相关方法获得的时延值，通过对比可以看出本文方法获得时延值的旁瓣更小，分辨率更高，时延值获取更准确.本文方法得到的每个时延估计值都是地面资料相对于井中资料的各个分量的时间差值，可以进一步求出地面资料各个分量的时延值，根据同行波时差定位法就可以反演出震源位置.

图7　 井中与地面原始数据

图8　 井中与地面波形及运用本文方法和互相关方法获得的时延估计对比

6　结　论

微地震监测资料受噪声干扰严重，本文提出的基于三阶累积量一维切片的方法能够有效地去除高斯噪声，获得时延估计值.通过仿真分析可以知道在添加随机高斯噪声和相关高斯噪声情况下，本文方法在时延拾取概率和均方根误差方面优于常规的相关方法，尤其在相关高斯噪声存在的情况下更能体现其优势.通过对实际微地震噪声的统计特性分析可知，实际噪声具有很强的高斯性.在实际的微地震资料处理中，选取了井中数据作为参考道，避免了选取地面数据作为参考道而受到噪声干扰大而获得的时延值不准确的问题.在信噪比很低的情况下，通过滤波等预处理可以更好地获得时延估计值.获得的时延估计值可以进一步得到地面不同道之间有效信号的时间差值，是后续微地震震源定位运算中的重要参数.

[1]宋维琪, 陈泽东, 毛中华. 水力压裂裂缝微地震监测 技术[M]. 东营: 中国石油大学出版社, 2008: 1-3.

SONGWei-qi,CHENZe-dong，MAOZhong-hua.Hydraulicfracturingcracksmicroseismicmonitoringtechnology[M].Dongying:ChinaUniversityofPetroleumPress, 2008: 1-3.(InChinese)

[2]梁兵, 朱广生. 油气田勘探开发中的微地震监测方法[M]. 北京: 石油工业出版社, 2004: 81-100.

LIANGBing,ZHUGuang-sheng.Microseismicmonitoringmethodsinoilandgasfieldexplorationanddevelopment[M].Beijing:PetroleumIndustryPress, 2004: 81-100.(InChinese)

[3]姜福兴, 杨淑华, 成云海, 等. 煤矿冲击地压的微地震监测研究[J]. 地球物理学报, 2006, 49(5): 1511-1516.

JIANGFu-xing,YANGShu-hua,CHENGYun-hai,et al.Astudyonmicroseismicmonitoringofrockburstincoalmine[J].ChineseJournalofGeophyics, 2006, 49(5):1511-1516.(InChinese)

[4]柳云龙, 田有, 冯噎, 等. 微震技术与应用研究综述[J].地球物理学进展, 2013, 28(4): 1801-1808.

LIUYun-long,TIANYou,FENGXuan, et al.Reviewofmicmseismtechnologyanditsapplication[J].ProgressinGeophysics, 2013, 28(4): 1801-1808.(InChinese)

[5]李振春, 盛冠群, 王维波, 等. 井地联合观测多分量微地震逆时干涉定位[J]. 石油地球物理勘探, 2014, 49(4) : 661-666.

LIZhen-chun,SHENGGuan-qun,WANGWei-bo, et al.Time-reversemicroseismichypocenterlocationwithinterferometricimagingconditionbasedonsurfaceanddownholemulti-components[J].OilGeophysicalProspecting,2014, 49(4):661-666.(InChinese)

[6]王晨龙, 程玖兵, 尹陈, 等.地面与井中观测条件下的微地震干涉逆时定位算法[J]. 地球物理学报, 2013, 56(9):3184-3196.

WANGChen-long,CHENGJiu-bing,YINChen, et al.Microseimiceventslocationofsurfaceandboreholeobservationwithreverse-tinefocusingusinginterferometrytechnique[J].ChineseJournalofGeophyics, 2013, 56(9): 3184-3196.(InChinese)

[7]EISNERL,ABBOTTD,BARKERWB,et al.Noisesuppressionfordetectionandlocationofmicroseismiceventsusingamatchedfilter[C]//SocietyofExplorationGeophysicists.LasVegas,Nevada:SEGAnnualMeeting, 2008:1431-1435.

[8]GIBBONSSJ,RINGDALF.Thedetectionoflowmagnitudeseismiceventsusingarray-basedwaveformcorrelation[J].GeophysicalJournalInternational, 2006，165：149-166.

[9]李希亮, 刘希强, 董晓娜, 等. 高阶统计量方法在地球物理学中的应用与展望[J].西北地震学报, 2010, 32(2): 201-205.

LIXi-liang,LIUXi-qiang,DONGXiao-na, et al.Applicationandexpectationofhigh-oderstatisticsingeophysics[J].NorthwesternSeismologicalJournal, 2010, 32(2): 201-205.(InChinese)

[10]尹成, 伍志明, 邓怀群. 高阶统计量方法在地震勘探中的应用[J]. 地球物理学进展, 2003, 18(3): 543-550.

YINCheng,WUZhi-ming,DENGHuai-qun.Applicationofhigh-orderstatisticsinseismicexploration[J].ProgressinGeophysics, 2003, 18(3): 543-550.(InChinese)

[11]冯智慧, 刘财, 冯晅, 等. 基于互四阶累积量一维切片的地震层位自动拾取方法[J].石油地球物理勘探, 2011, 46(1): 58-63.

FENGZhi-hui,LIUCai,FENGXuan, et al.Anautomaticseismichorizonpicking-upmethodbasedononedimensionalsliceofcrossfourthordercumulant[J].OilGeophysicalProspecting, 2011, 46(1): 58-63.(InChinese)

[12]熊晓军, 尹成, 张白林, 等. 高阶统计量油气检测方法研究[J]. 地球物理学报, 2004, 47(5): 920-927.

XIONGXiao-jun,YINCheng,ZHANGBai-lin, et al.Methodresearchofforecastingoilandgasusinghigher-orderstatistics[J].ChineseJournalofGeophyics, 2004, 47(5):920-927.(InChinese)

[13]唐斌, 尹成. 基于高阶统计的非最小相位地震子波恢复[J]. 地球物理学报, 2011, 54(3): 404-410.

TANGBin,YINCheng.Non-minimumphaseseismicwaveletreconstructionbasedonhigherorderstatistics[J].ChineseJournalofGeophyics, 2011, 54(3): 404-410.(InChinese)

[14]宋维琪, 杨勤勇, 郭全仕,等. 地面微地震资料弱信号提取方法研究[J]. 石油物探, 2013, 52(2): 131-135.

SONGWei-qi,YANGQin-yong,GUOQuan-shi, et al.Weaksignalextractionmethodforsurfacemicroseismicmonitoringdata[J].GeophysicalProspectingforPetroleum, 2013, 52(2): 131-135.(InChinese)

[15]张贤达. 时间序列分析—高阶统计量方法[M]. 北京: 清华大学出版社, 1996: 328-335.

ZHANGXian-da.Timesequenceanalysis[M].Beijing:TsinghuaUniversityPress, 1996: 328-335.(InChinese)

[16]张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2002: 1-20,407-410.

ZHANGXian-da.Modernsignalprocessing[M].Beijing:TsinghuaUniversityPress, 2002: 1-20,407-410.(InChinese)

[17]蒋忠进, 林君, 陈祖斌. 三阶累积量在可控震源勘探信号处理中的应用[J]. 系统工程与电子技术, 2003, 25(11): 1431-1434.

JIANGZhong-jin,LINJun,CHENZu-bin.Theapplicationofthree-ordercumulantintheprocessingofvibratordata[J].SystemsEngineeringandElectronics, 2003, 25(11): 1431-1434.

[18]NIKIASCL.Timedelayestimationinunknowngaussianspatiallycorrelatednoise[J].IEEETransactionsonAcousticsSpeechandSignalProcessing, 1988, 36(11): 1706-1714.

[19]柯宏发, 陈永光, 张哲峰. 基于四阶累积量对角切片的短波自适应通信信号检测[J]. 电子学报, 2006, 34(3): 419-423.

KEHong-fa,CHENYong-guang,ZHANGZhe-feng.HFadaptiveradiocommunicationsignaldetectionbasedonfourth-ordercumulantsdiagonalslice[J].ActaElectronicaSinica, 2006, 34(3): 419-423.(InChinese)

[20]GROOSJC,RITTERJRR.Timedomainclassificationandquantificationofseismicnoiseinanurbanenvironment[J].GeophysicalJournalInternational, 2009,179(2):1213-1231.

Time Delay Estimation of Microseismic Signal Based on One-dimensional Slice of Three-order Cumulants

CHEN Zu-bin1,2，LIU Xin1，SUN Feng1,2†，LV Hao1，WANG Dong-he1

(1.College of Instrumentation and Electrical Engineering, Jilin Univ,Changchun,Jilin130061,China;2.Key Laboratory of Geo-Exploration and Instrumentation of Education Ministry, Jilin Univ, Changchun,Jilin130061, China)

The effective microseismic signals are disturbed by noises, so the precision of time delay estimation is affected. Because time delay estimation is the key to determine location accuracy, one dimensional slice method based on third-order cumulants was proposed for microseismic signal time delay estimation. Firstly, the three-order self accumulation and mutual accumulation of the signals were calculated, then, one dimensional slice was obtained in order to reduce the computation and to satisfy the field real-time requirements. Finally, the time delay value was obtained by the criterion function. Compared with the traditional cross correlation method, this method has less sensitivity to the Gauss noise with unknown correlation and has stronger inhibition ability to the correlated Gauss noise. The simulation results show that the detection probability and root mean square error are better than the traditional method under the influence of Gauss random noise and correlated noise with SNR=-5 dB to SNR=15 dB. In the implementation of real data, the real microseismic noise probability statistic characteristics were analyzed and the data in the well were selected as references, and then the time delay value to the ground data was calculated on the basis of the surface and borehole observation. The validity and the practicability of this method were verified.

parameter estimation; noise suppression; three-order cumulants; microseismic monitoring; one dimensional slice

1674-2974(2016)08-0120-08

2015-04-15

国家自然科学基金资助项目(41074074，41074082，41304139)，National Natural Science Foundation of China (41074074，41074082，41304139)

陈祖斌(1971-)，男，湖南澧县人，吉林大学教授，硕士生导师†通讯联系人，E-mail: sunfeng@jlu.edu.cn

TE319

A