立足解法对比,培养求简意识——以一道填空题教学为例
2016-09-09江苏省连云港市新海实验中学凤凰校区周绪光
☉江苏省连云港市新海实验中学凤凰校区 周绪光
立足解法对比,培养求简意识——以一道填空题教学为例
☉江苏省连云港市新海实验中学凤凰校区周绪光
培养学生的“求简”意识,是初中数学教学的一项重要任务.便捷的解题方法和简约的解题过程,能为学生的问题解决节约大量的时间和精力,对他们取得较好的评价结果非常有利.因此,我们应以每一次例题或练习的讲评为契机,在不同解法的对比分析中培养学生优选解法的意识,促使其形成找寻解题捷径的能力和习惯.在实际教学中,老师们一般比较重视解答题的解法教学,对填空或选择这两类题型的解法分析不够,往往抱着“只要能得到结果,过程无所谓”的态度进行讲评交流,这对学生优解意识和优解能力的形成是十分不利的.现结合一道填空题的教学,谈谈笔者的做法与思考,说得不对之处,敬请批评指正.
一、一道填空题的教学历程及分析
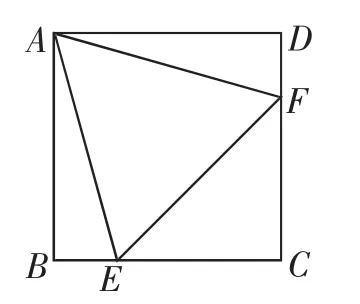
图1
(一)题目及分析
题目如图1,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,则正方形ABCD的面积为_____.
分析:本题改编自2013年山东省德州市中考卷第17题,原题为填空“压轴题”,其难度较大.基于“题目”所给条件,原题共给出了结论“①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=,要求学生将正确的序号填在题中的空格处.在例题设计时,为了契合“平行四边形”单元复习的课时目标,笔者对试题进行了改编,删去了原来的四个结论,直接让学生求“正方形ABCD的面积”,以此引导学生回顾正方形及其相关知识.想要顺利解答本题,学生必须能从自己的知识网络中提取出正方形、等边三角形的性质,全等三角形的判定及性质,勾股定理等知识,并灵活应用.
(二)教学过程及分析
1.教学过程
(1)自主解答.
学生活动:自主解答,并思考解题中用到的知识、数学思想方法和解题的注意点.
(2)解法交流.
学生根据要求先自主解答,然后在小组中交流.6分钟后,教师组织学生在全班交流.
学生1将自己的求解思路(下称方法1)进行了展示:利用正方形和等边三角形的性质得到AB=AD,AE=AF,所以Rt△ABE≌Rt△ADF.根据全等三角形的性质可得BE=DF,所以CE=CF.根据“等边三角形边长为2”可得AE=AF=EF=2,易得.设正方形的边长为a,应用勾股定理可得AD2+DF2=AF2,即
此时,学生2说:“这个方法太繁了”,教师示意学生2让学生1先说完,然后再交流.
接下来,教师请学生2将自己的思路(下称方法2)也进行了交流:在得出“BE=DF,CE=CF”后,连接AC交EF于点O.根据“到一条线段两个端点距离相等的点在这条线段的垂直平分线上”和“两点确定一条直线”可证得AC垂直平分EF.根据AE=AF=EF=2,应用“三线合一”和“勾股定理”可以求得,所以,对角线AC=利用正方形面积的“对角线”求法,可以求得
(3)对比分析.
教师请两名同学分别将自己求解的“后半段”(即解法中不同的地方)板书在黑板上,并请下面的同学进行比较,发现两者的区别和联系,选择自己认为简洁的方法.学生将自己对两种不同解法的看法、自己选择的解法及选择的缘由,都在小组中进行了交流.3分钟后,教师组织学生进行了全班交流,在肯定了两位同学的精彩展示的同时,也对两种方法的优势进行了剖析:方法1,紧扣直角三角形这一条件,用勾股定理构造方程,是解答此类问题较为常见的途径;方法2,充分利用菱形(正方形)的性质,将面积转化为“对角线乘积的一半”,对本题而言是一种很实用的技巧,简化了思路分析和求解的过程,是个不错的方法.两者比对,对本题的解答而言,方法2是优于方法1的.
2.过程简析
例题是一道涉及多个知识点的综合题,其难度较大,将其用以巩固正方形的性质是十分合适的.教师沿着预设的三个环节对例题进行了巧妙的解读,取得了较好的教学效果.
首先,安排了学生的自主解答,学生对例题进行自主分析、解答后,明确了题目的条件和结论,初步形成问题解决的思路和过程,对教师提出的思考“解题中用到的知识、数学思想方法和解题的注意点”也有着自己的认识.这样的设计,让学生的解答与思考同步,对问题的理解是深刻的、个性化的.
第二个环节是解法交流,主要是呈现不同的解题方法,积累交流资料.教师引导学生展示的是本题较为常用的两种解法,最先呈现的是方法1,此法是学生的“自然解法”,很多学生能够想到,因而在学生中大有“市场”.然而,学生2十分直白地告知大家:“方法1太繁了”!在学生1展示完第一种解法后,由其口述了更为简洁的方法2.学生1、2的口头陈述,为下一步交流积累宝贵的资料.
最后,是教师引导下的对比分析,既包括学生的自我对比分析,也包括教师的总结分析.由于口述的解法并不详实,且不利于比对,教师要求学生将这两种解法的“差别”进行了板书,并让学生进行比较,找出两者之间的区别和联系,进而找出“自己认为最简洁的方法”.最后是教师结合学生的交流发言进行总结,两种解法的点评让学生认清了解法的简与繁、优与劣.
细细分析教师的教学历程,我们不难发现,教师将教学的主要精力集中在解法的交流与对比分析上,对两种解法的优与劣进行了较为详实的剖析,这样的教学,有利于培养学生的多解意识和求简意识,对学生分析问题和解决问题能力的提升是有益的.
二、三点感悟
1.重视过程剖析,培养求简意识
数学问题中,不同的题型有着不同的特点.例题教学,在关注题型分析的同时,更应关注学生在问题解决中的结果获得过程的分析.口述、板书等方式,都是展示学生分析问题和解决问题能力的较好的途径.在这些方式下的交流,重在解题思路获得过程和解题方法的直观呈现,唤醒了学生分析问题的过程,是对不同学生解题分析差异性的最直观的体现,有利于学生发现自己的解题过程与他人之间的差别,激活学生内在的求简意识,通过接下来的对比教学将会让这一意识得到进一步强化,使之扎根在学生思考解题思路的过程之中,成为其问题解决的习惯性思维.我们可以结合上面的案例来看,教师给了两位学生展示自己解题过程的机会,通过口述过程和板书展示,每一名学生都参与了他们的问题解决过程,同时对自己的求解过程同样也有着自己的反思,其求简意识也就自然得到了进一步强化.
2.强化解法对比,彰显简法优势
有对比,才有鉴别.解法比对,是学生“求简意识”养成的必经之路.当我们将不同的解法以口述展示或板书直观呈现时,学生便可以从中看到解法的差别之处,发现简洁解法的优势所在,使其产生强烈的羡慕、渴望的积极心理状态,从知识、情感和态度上为求简意识的形成积累“素材”.上面的方法1、2,差异是非常明显的,教师非常敏锐地捕捉到这两者之间的差异,不仅让两个学生分别说,还让他们将两种解法中有差异的部分直接写在了黑板上,如此直观的展示,让解法及其形成过程完整地“显现”,给学生的对比分析提供了极大的便利.接下来,个人的自我反思、全班交流及全部交流都将围绕着黑板上(学生陈述的)两种方法展开,如此自然的教学生成,凸显出了解法的优势所在,“倒逼”着学生去体会与应用最简的分析问题的方法和解决问题的方法,从而逐步养成求简意识和应用意识.
3.教学因时而异,渐进发展能力
求简意识的形成,与学生所具备的知识基础有着很大的关系.在数学教学活动中,随着数学知识的不断积聚,学生的求简意识和求简能力也会逐步增强.知识的系统化程度越高,个体的求简意识越强,求简能力越高.因此,我们应将例题设置在合适的教学时点上,力求以解法的对比和自我的感悟,来提升个体问题解决的能力.基于这样的理解,在同一知识的不同教学时点上,我们应编排综合程度由低到高的教学例题,精心设计教学过程,将能力培养逐步落实到教学进程之中.以本文中的例题为例,这道题综合性较强,如果编排在学生刚刚获得正方形知识后的“巩固练习”中,如此大的难度显然是不适宜的;教者将其编排在正方形的复习课上,关于正方形的知识已经在学生的认知网络中扎下了根,与很多前面学过的数学知识产生“链接”在了一起,此时将题目进行教学应用显然是再适宜不过的.加之,教师为例题精心预设了与学生认知发展规律契合的教学流程,学生成为了互动交流的主体,他们在教师所搭建的平台上将个人的解法及对不同解法的理解尽情阐释,效果是显著的.
三、写在最后
例题教学的指向是多维度的,其核心是指向“四基”的,如巩固基础知识,训练基本技能等.求简意识,是学生基本活动经验的重要组成部分.较强的求简意识和求简能力,将能帮助学生在今后的问题解决中寻找捷径,“走近路”.培养学生的求简意识与求简能力的过程,也是提升学生的“四能”和数学素养的过程.因此,我们的数学教学应在突出数学“四基”核心教学基础之上,将求简意识与能力的培养穿插其中,以有效的引导和比对让学生深刻领会其价值,进而成为问题解决过程中的一种自觉意识.
以上所述,仅一家之言,不足之处,敬请各位同行专家批评指正.
