活化教材,注重过程,突出文化——人教版八年级下册“函数”的教学设计
2016-09-09湖北武汉第三寄宿中学桂文通
☉湖北武汉第三寄宿中学 桂文通
活化教材,注重过程,突出文化——人教版八年级下册“函数”的教学设计
☉湖北武汉第三寄宿中学桂文通
去年上半年,本人有幸成为我区优质课比赛的评委,这次比赛的课题是人教版八年级下册“函数”,我想结合本次比赛情况和观课的感受,谈谈对本节课教学再设计的建议,希望能给大家一定的启发.
一、创设问题情境,激发学习兴趣
数学是模式的科学,书本上的数学知识大部分都割裂了与现实的联系,失去其直观背景,而成为量化的模式.这就使得学生面对的是抽象的数学知识,而不能体会数学知识从现实中产生所需要的数学观念与意识,失去了从数学角度观察、分析现实问题的机会.而问题情境的创设,实际上是一个返璞归真的过程.问题情境能够调动学生思维的积极性、求知欲和创造欲,“一个恰当而富有吸引力的问题往往能拨动全班学生思维之弦,奏出一曲耐人寻味,甚至波澜起伏的大合唱.”所以,我们教师有义务给学生创设合适的问题情境.
结合本节教学内容,可设计如下几种问题情境.
情境1:(“嫦娥二号”升空)通过“嫦娥二号”升空视频,让学生感受时间与高度两个变量的变化和对应关系(如下表).

飞行时间/秒 129 146 257 332 1533离地面的距离/公里 1399.39 1583.81 2787.94 3601.54 16630
该情境不但让学生直观感受两个变量的变化过程,而且让学生感受到祖国的伟大成就,增强对国家发展越来越强大的自豪感和荣誉感,突出情感目标的实现.
情境2:(“乌鸦喝水”的故事)通过“乌鸦喝水”的故事,让学生感受石子的数量与瓶中水的高度的变化和对应关系.播放动画片《乌鸦喝水》,已知瓶子里的水已有5cm高,平均一粒石子让水升高3cm.
(1)思考:在这则故事中,哪些量是常量,哪些量是变量?
(2)填表:

x/粒1 2 3 4 … x y/cm 8 11 14 17 … y=5+3x
观察表格,让学生发现每当石子数x取定一个值时,水位高度y就随之确定一个值,自然引出课题.
该情境充满童趣,很容易激起学生探究问题的欲望.通过动画,复习旧知,引出新知.
情境3:(名探柯南的故事)通过名探柯南的故事,让学生感受疑犯的脚印长与其身高的变化和对应关系.《名侦探柯南》中有这样一个情景:柯南根据案发现场的脚印,锁定疑犯的身高.你知道其中的道理吗?请同学们一起玩一个破案游戏.
有关资料表明:脚印长与身高有如下数量关系:

脚印/cm 22 23 24 …身高/cm 154 161 168 …
(1)若脚印长度为26厘米,身高长度为多少厘米?
(2)若令脚印长度为x厘米,身高长度为y厘米,求y 与x之间的关系.
用数学知识破案,太有意思了,学生怎么会不集中注意力呢,这大大激发了他们的学习兴趣.
情境4:(密码破译问题)通过“二战”中密码破译的历史故事,让学生感受暗码和明码的变化和对应关系.二战中美军破译了日军密码,派战机伏击,击落了日本海军大将山本五十六的座机,重挫了日本法西斯军国主义对世界人民的侵略.
下面就是美军截获和破译的密码中的一小段:
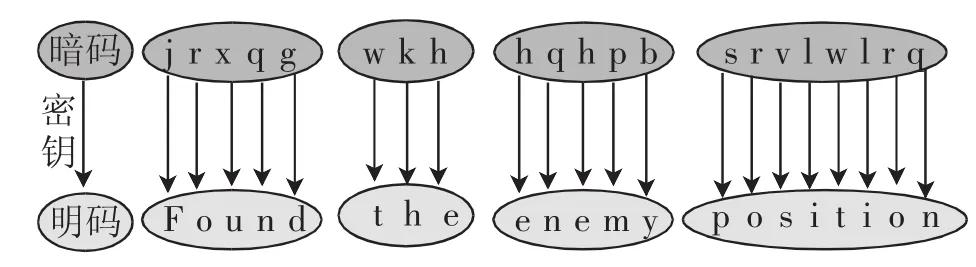
图1
用历史小故事,让学生体会数学与军事的密切联系,激发学生的求知欲,宣扬爱好世界和平的良好情感,为新课的开展营造良好的学习氛围,启发学生要善于从数学角度去观察生活和思考问题.
真实、合理的问题情境,可有效揭示初中阶段的函数本质——“变量说”.这些情境生动有趣,充满时代感和生活性,将学生引入问题状态,有效地调动了学生思维的积极性,激发了学生的学习兴趣和动机,为学生后继的概念学习搭建了一个很好的“脚手架”,学生也感到数学有用、有趣,提高了课堂效率.
好的开端,往往是一堂课成功的开始!
二、重视数学过程,获取函数概念
数学就是人们对客观世界的定性的把握和定量的刻画,逐渐抽象概括,形成方法和理念,并进行广泛应用的过程.概念教学的核心是引导学生开展概括活动,将凝结在数学概念中的数学思维活动打开,以若干典型具体实例为载体,引导学生展开分析各实例的属性、抽象概括共同本质属性、归纳得出数学概念等思维活动而获得概念.概念教学要让学生经历概念的概括过程,一般有如下几个基本环节.(1)背景引入;(2)具体实例的属性分析、比较、综合;(3)概括共同本质特征得到概念的本质属性;(4)下定义(准确的数学语言描述);(5)概念的辨析——以实例(正例、反例)为载体分析关键词的含义;(6)用概念作判断——形成用概念作判断的“基本规范”;(7)概念的“精致”——建立与相关概念的联系.
上面几个环节,课堂上可以如下实施.
(1)情境引入(略).
(2)通过教师提供的生活中的实例或学生自己身边的实例,抽象出函数关系.比如:
a.行程问题中路程S与时间t:S=60t;
b.弹簧的长度L与挂物重量m:L=20+4m;
c.圆的面积S与半径r:S=πr2;
……
【通过大量的生活中一个量随着另一个量的变化而变化的实例,让学生体会在这种变化过程中两个变量之间的关系,逐步建立函数概念.】
(3)引导学生分析上面函数的特征.提炼出函数的三要素:函数是研究一个变化的过程,它反映的是两个变量间的一种数量关系,当一个变量的值确定时,另一个变量也唯一确定(唯一性).
(4)概括函数概念.结合函数的三要素,概括出函数的基本定义.
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是自变量的函数.
(5)概念的辨析与判断,巩固概念,“回到定义中去”.可设计下面一组变式训练.
练习1:下列三种情况中,你能用x表示y吗?y是x的函数吗?为什么?
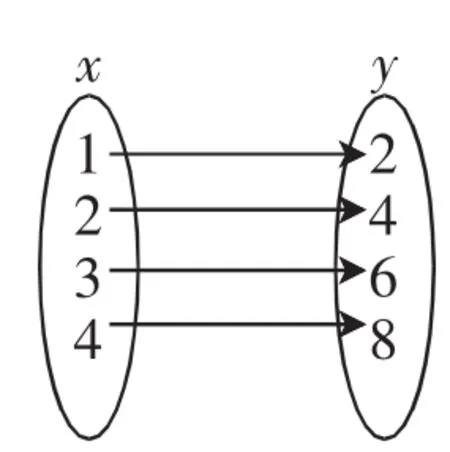
图2
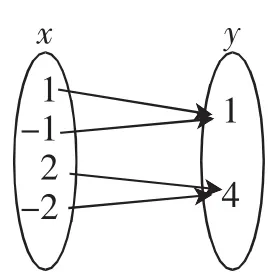
图3
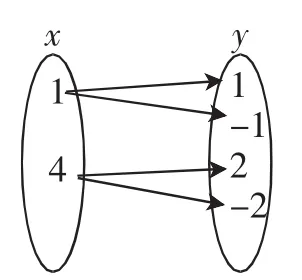
图4
(1)如图2,左边的数都乘以2后,得到了右边的数;
(2)如图3,左边的数平方后,得到右边的数;
(3)如图4,左边的数开方后,得到右边的数.
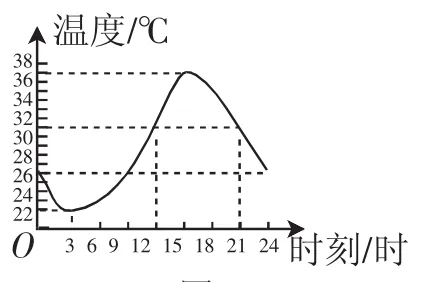
图5
练习2:图5是武汉某天的气温变化曲线,时刻t的变化引起温度T的变化.
(1)T是t的函数吗?为什么?
(2)t是T的函数吗?为什么?
练习3:在分数统计表中,分数是考号的函数吗?

考号 0001 0002 0003 0004分数 120 116 96 106
练习4:如图6,给出变量y与x的关系,请依次指出y是否是x的函数.
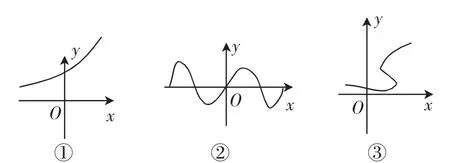
图6
【函数概念的理解是本节课的难点.首先,对函数概念中的“每一个”“唯一确定”等关键词理解难以到位,教学中可以从正、反两个方面识别函数,从数与形的角度认识函数(还可以介绍心电图曲线、股市K线图等),帮助学生理解;其次,对于学生来说,接触的主要是用解析式表示的函数,他们对图像、图表表示的函数,因为难以找到判断的标准,所以在图像、图表中,我们要重视“变量说”中“唯一性”的特征.另外,在函数的识别中,我们也可以渗透它的三种表示方法,即解析法、图像法、列表法.这样可有效地突出教学重点、突破教学难点.】
(6)概念的“精致”阶段.在教学过程中,可以比较函数与自变量的区别,以及函数与函数值的区别.
(7)介绍函数在生活中的简单应用.
例1(教材第73页)一辆汽车油箱现有汽油50L,如果不再加油,那么油箱中的油量y(L)随行驶里程x(km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系式;
(2)指出自变量x的取值范围;
(3)汽车行驶200km时,油桶中还有多少汽油?
【例1是函数在实际生活中的简单运用,不但巩固了变量与函数等概念,让学生体会到生活中许多问题都存在着函数关系,还揭示了现实世界中数量关系之间相互依存和变化的实质,是刻画和研究现实世界变化规律的重要模型.通过问题的解决,让学生体验用函数观点处理身边问题的过程,体会用函数观点构建数学模型对于处理实际问题的高效与实用.通过变量之间的关系,能使学生进一步审视已有的代数式、方程、不等式的知识及其联系,增强综合应用知识的意识,提高分析问题和解决问题的能力.】
至此,在函数概念的教学过程中,突出了数学过程,在头脑创造中还原生命活力,让静态的数学概念,呈现出丰富的数学内涵、数学思考、数学观念.在探索和发现的过程中,学生体会到数学概念的提出过程,知识的形成和发展过程,使学生在这些过程中“火热的思考”,欣赏到形式化概念中“冰冷的美丽”.
三、重组教学素材,凸显教师智慧
新的课程标准提出:“教材内容的选择应符合课程标准的要求,体现学生的身心发展特点,有利于引导学生利用已有的知识与经验,主动探索知识的发生与发展,同时也有利于教师创造性进行教学.”我们教师不仅是教材的使用者,还应该是教材的开发者.叶圣陶先生也说过:“课本只是一个例子”.我们教师可以根据课本这个例子,创新地使用教材,不要一味地“教教材”,要有很强的“用教材”意识.
比如一位老师根据教学内容,设计了一个“小明同学到森林公园去烧烤”问题串,给零碎的问题赋予一定情节,突出教学设计的整体感.她的三个问题如下所示.
探究1:(购物)在家附近超市,小明打算用8元钱去购买同一款火腿肠.粗的0.5元/根,细的0.4元/根,单价与购买数量之间有什么关系?
探究2:(乘车)小明乘以40千米/时的速度匀速行驶的公交车去森林公园,用t表示它行驶的时间(小时),用S表示它行驶的路程(千米),S与t有什么关系?
探究3:(在公园玩)扔一个石子到水里,荡开圆形水波纹的面积S与半径r有怎样的关系?
在三个问题中,自然地引入了初中学习的三类函数(反比例函数、一次函数、二次函数).
还有一位老师在整个课堂中都是围绕“世博”设计问题,突出“世博”文化主题,也很好地体现了数学的现实性.他设计的一组问题如下所示.
问题1:小明从武汉乘动车组去上海,如果动车组以250千米/时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时,用含t的式子表示s为___________;
问题2:小明在早上10点进入世博园时了解到园区现在有8万人,如闸门每小时平均净放入3万人,则t小时后园内的人数n(万人)可以表示为_________;
问题3:德国馆前要用200米的栏杆围成一个长方形的休息场地,如一边长为x米,面积为y平方米,用含有x的式子表示面积y为_____________;
问题4:由于每天参观世博会人数众多,很多场馆必须长时间排队进入.某个商店每天销售6000个折叠小凳,平均每小时卖m个,t小时卖完,用含有t的式子表示m 为_________.
其实,还可以根据教学的需要,将课本上的问题有意识地进行改造或分解,创造性地挖掘教材,极大地凸显教师的智慧.比如有老师对例1重新设计为如下5个小问题:
(1)写出表示y与x的函数关系的式子;
(2)汽车行驶200km时,油箱中还有多少汽油?
(3)汽车行驶多少千米后油箱中还有油12L?
(4)汽车最多行驶多少千米?
(5)指出自变量x的取值范围.
对照教材上的安排,增加了问题(3)、(4),并把问题(5)放置最后.问题(3)、(4)的增设,即已知函数值,求自变量的值,不但帮助学生理解函数的“单值对应关系”,而且渗透了函数与方程的联系,还为问题(5)的解决作了铺垫.
四、文化润泽课堂,绽放理性之光
数学是人类的一种文化,它的内容、思想、方法和语言是现代文明的重要组成部分,《数学课程标准》指出:数学教学应当承担向学生传递数学文化的重要职责,教师应有意识地在数学课堂上渗透数学文化,让数学这个学科绽放出应有的理性光辉,努力构建“以智生情”的数学文化课堂.重视数学数学思想方法的教学,让课堂充满数学味.在课堂上,我们要充分挖掘出教材中隐藏的数学思想方法,并且将它放大、外化,并在课堂中予以传递,让它成为学生进行数学思考的重要支撑.比如在本节教学中,可以适时地渗透函数、数形结合、数学建模等思想方法.引入数学史,凸显人文课堂.适当地介绍函数概念的发展历史、函数一词的由来和一些数学家(比如欧拉)的故事,这样做不但使学生了解函数概念的发展过程,而且还让他们从数学家的身上获得一种精神力量,引导学生透过史实,触摸到史实背后的价值和观念,使其构成一种更有教育意义的积极影响.
另外,通过数学与生活的联系,让学生感受到数学来源于生活,又服务生活这一辩证唯物主义观,也体现了数学的应用之美,让学生感受到数学的力量.
构建民主、平等的生态课堂也是课堂文化的一部分.教师要始终为学生创设一种师生平等、民主的课堂氛围,师生平等对话,充分调动学生的积极性,让学生积极参与教学活动.教师还要运用激励性评价,帮助学生更好地认识自我,建立学好数学的信心.一位老师用“聪明是勤奋的函数”结束新课,意味深长,不但点明课题,而且启迪人生.
正是教育对人的生命存在及其发展的整体关怀,使得学生在课堂上表现得精神饱满、自信专注,师生间才有心灵的碰撞、思路的交锋,使得课堂教学焕发出无穷的生命力.
参考文献:
1.李延林.理解教材是设计教学的重要基础[J].中学数学教学参考(下),2008(7).
2.吴琳.关于教材整合的一些思考[J].中国数学教育(初中版),2015(12).
3.冯菊美.从一堂优质课谈“过程化”教学的实施[J].中学数学教学参考(下),2008(12).
