坝体地震记录峰值加速度特性分析

钟菊芳，胡　晓，杨荣来

(1.南昌航空大学土木建筑学院，江西南昌330063；2.中国水利水电科学研究院工程抗震研究中心，北京100044)



坝体地震记录峰值加速度特性分析

钟菊芳1，胡晓2，杨荣来1

(1.南昌航空大学土木建筑学院，江西南昌330063；2.中国水利水电科学研究院工程抗震研究中心，北京100044)

针对目前地震工程中建议用有效峰值加速度(EPA)代替最大峰值加速度(PGA)的现状，以克孜尔大坝为例，通过对地震记录资料的统计分析揭示坝体地震响应的PGA与EPA间的内在联系和统计特性，以及EPA与PGA随震级、震中距的衰减规律，探讨坝高对PGA和EPA的影响规律，为大坝抗震计算分析中加速度峰值的合理选用和预测提供理论依据及实用模型。

地震记录；PGA；EPA；衰减规律；相关性

0　引　言

克孜尔大坝位于新疆拜城县克孜尔乡，坝区地质构造复杂，地震异常活跃且集中分布在拜城盆地及库车坳陷内[1]，黑孜尔断层自西向东穿越克孜尔水库库区、主坝左坝肩及副坝右坝肩，克孜尔大坝是我国首例建造在活动断层上的水利工程[2]。地震是克孜尔水库工程安全运行的主要潜在危险。为了更好地监测大坝在强震作用下的安全，2004年在坝址区安装了地震监测台阵。该台阵已获得85次地震记录，为开展大坝地震响应分析提供了宝贵的数据资料。

地震加速度峰值是抗震设计中的一项重要参数，取值是否合理直接影响抗震设防的标准和基本建设投资。不少学者[3- 5]开展了地震动峰值特性的研究。由于最大峰值加速度(PGA)通常指加速度时程的最大值，常由地震动的高频成分所决定，不是反映地震作用的理想抗震设计参数，工程界建议使用对结构反应有明显影响的有效峰值加速度(EPA)来描述地震动的峰值特性[3，6]。针对目前国内规范在PGA与EPA的采用方面存在不协调的现状，以克孜尔主坝0+180断面上的坝基(2- 3)、坝坡(2- 2)及坝顶(2- 1)3个测点[2]的地震记录为基础，就PGA、EPA及其比值间的统计特性、衰减特性以及相关性进行探讨，得到PGA和EPA的统计规律和衰减式，论证用EPA取代PGA的可行性和两者间的相互转换关系，便于工程设计人员合理选用PGA、EPA及与现行规范的配套使用，并通过地震分组揭示大小远近地震对PGA、EPA的影响规律，为大坝安全运行、抗震设计及维修加固数据基础和理论提供依据，最大程度地减轻震害，防止次生灾害的发生。

表1同一测点不同分量间PGA比值

注：NS、EW及UD分别表示水平南北、东西及竖向地震分量，Max.、Min.μ、σ及分别为最大值、最小值、均值及方差。

1　峰值加速度比值关系分析

1.1同一测点不同分量间峰值加速度比例关系

表1给出了同一测点不同分量间峰值加速度PGA及EPA比值的统计结果。

从统计结果来看，不同地震、同一测点不同地震分量间PGA、EPA值及其比值差异显著，测点高度对峰值及其比值的影响不显著。如近场小震坝坡记录PGANS/ PGAEW、PGANS/PGAUD、PGAEW/PGAUD、EPANS/EPAEW、EPANS/EPAUD以及EPAEW/EPAUD最大值与最小值间的差异分别达5.3、37.0、12.1、4.4、10.3及4.8倍。除近场小震坝基竖向分量的PGA大于水平分量、坝坡东西与南北分量的PGA相近外，其余情况的PGA和EPA均为水平分量大于竖向分量，东西分量大于南北分量；东西与南北分量的PGA及EPA比值均随测点高度的增加而增加。

同一测点不同分量间近场小震与远场中强震的峰值统计平均结果的差异在于：远场中强震比近场小震的峰值比大；坝基近场小震的竖向分量大于水平分量，东西分量大于南北分量；坝基远场中强震水平分量远大于竖向分量，且两水平分量差异较小。

1.2不同测点相同分量间峰值加速度比值关系

不同测点相同地震分量PGA、EPA差异显著。PGA和EPA随测点高度变化的规律基本相同，即随坝高的增加而变化。其中，坝高对坝顶的地震响应影响显著，对坝坡地震响应的影响规律不一致。坝顶的峰值比坝坡及坝基的大，坝顶具有较大的放大效应。坝坡近场小震的东西和竖向分量的EPA值，以及远场中强震的东西和南北分量的PGA和EPA值均小于坝基的对应值，其余则表现为坝坡的PGA和EPA值大于坝基的。显然，坝坡跟坝基相比，不存在明显的放大效应。

1.3同一测点相同地震分量间的PGA与EPA比值关系分析

同一测点相同地震分量间的PGA/EPA>1，近场小震的PGA/EPA大于远场中强震的对应值。远场中强震的PGA/EPA除坝基竖向分量最大外，其余均为坝坡的最大；近场小震坝顶测点的PGA/EPA除东西分量外，其余情况均为最小。说明坝顶的PGA与EPA值最为接近，坝坡的PGA值与EPA值的差异最大，PGA/EPA随坝高变化的规律为先增后减。

2　峰值加速度及其比值随震级和距离的变化规律分析

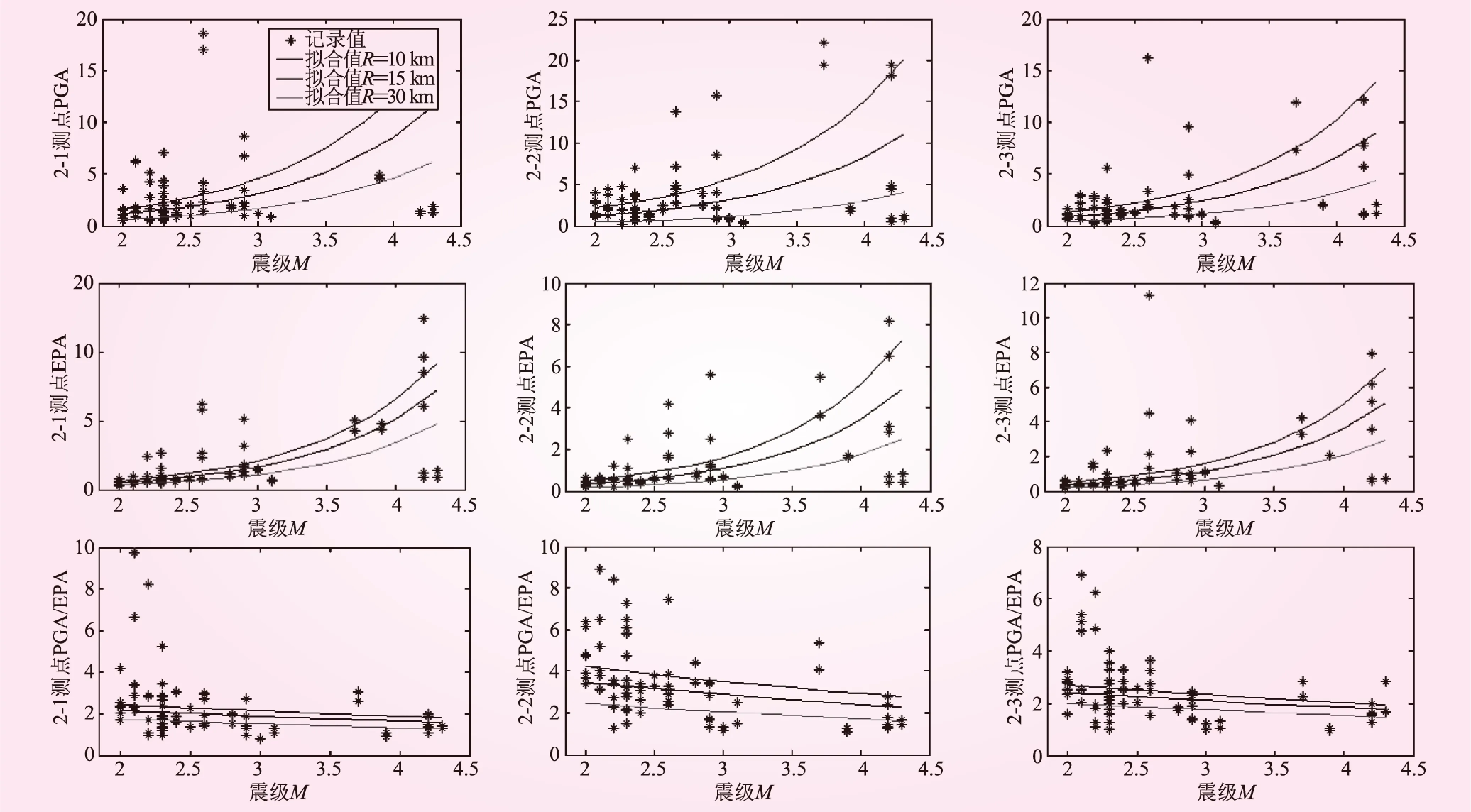
图1　坝体记录PGA、EPA及PGA/EPA随M和R变化的散点和拟合曲线(2.0≤M<4.5且R≤60 km)

图2　PGA、EPA及PGA/EPA随M和R变化的对比

近场小震和远震中强震震级饱和效应不明显，采用如下的衰减关系式进行分析：

lgY=c1+c2M+c3lgR

(1)

式中，Y代表PGA、EPA或PGA/EPA；M为震级；R为震中距；ci(i=1,2,3)为衰减系数。

采用非线性最小二乘法拟合得到了衰减系数。图1、图2为近场小震水平分量的PGA、EPA及PGA/EPA随M和R变化的拟合图。

从图1、2可以看出，PGA及EPA均随M增加和R的减小而增加；近场小震的PGA/EPA随M和R增加而减小。远场中强震除坝坡水平分量的PGA/EPA随M增加和R减小而减小；坝顶及坝基水平分量的PGA/EPA均表现为随M增加和R减小而增加。

表2相同测点的PGA和EPA间相关性分析结果

分析变量yx测点编号相关系数置信水平相关t值置信水平回归系数ab回归方程F值置信水平PGAEW-NSEPAEW-NS2-10.9280.99927.6600.9951.3070.718765.0900.9952-20.9510.99934.3710.9952.601-0.1551181.4000.9952-30.9240.99926.8210.9951.6740.319719.3450.995PGAUDEPAUD2-10.9190.99918.1950.9952.041-0.017331.0480.9952-20.8960.99915.7390.9993.533-0.096247.7110.9952-30.9240.99918.8210.9953.113-0.069354.2160.995PGAEWPGAUD2-10.8050.99910.5840.9951.143-0.604112.0290.9952-20.9230.99918.6620.9990.8530.464348.2500.9952-30.5770.9995.5170.9950.9281.22330.4410.995PGANSPGAUD2-10.9240.99918.8760.9950.862-0.614356.3000.9952-20.9350.99920.6000.9991.0280.017424.3710.9952-30.9260.99919.0780.9951.251-0.629363.9840.995PGAEWPGANS2-10.9450.99922.5690.9951.438-0.474509.3520.9952-20.9310.99919.9610.9990.7830.661398.4280.9952-30.7850.9999.8870.9950.9330.79897.7450.995EPAEWEPAUD2-10.9750.99934.2450.9950.764-0.1641172.7000.9952-20.9620.99927.3450.9990.6320.104747.8000.9952-30.8820.99914.5850.9950.775-0.103212.7130.995EPANSEPAUD2-10.9670.99929.6510.9950.614-0.072879.1690.9952-20.9850.99944.6940.9990.7250.0521997.5000.9952-30.9740.99933.5390.9950.699-0.0401124.9000.995EPAEWEPANS2-10.9830.99942.3390.9951.213-0.0581792.5000.9952-20.9750.99934.1130.9990.8700.0741163.7000.9952-30.9270.99919.2790.9951.135-0.143371.6910.995

此外，还可以看出，不同测点的PGA、EPA及PGA/EPA随M和R的衰减速度不同，大小地震的衰减规律也不相同。近场小震坝顶和坝坡的水平分量PGA为大于坝基；坝顶和坝坡PGA值随M增加而增加的幅度大于坝基；近距离(R=10 km)处坝坡PGA大于坝顶，R=15 km处两者相当，R=30 km处则坝顶大于坝坡。EPA随M增加而增加的幅度坝顶大于坝基，坝坡与坝基相当。坝顶PGA/EPA值小于坝坡和坝基，随M增加而减小的幅度也更小；坝坡PGA/EPA大于坝基，且随M增加而减小的幅度也更大。PGA和EPA随R增加而衰减的速度以坝坡最快，坝基其次，坝顶最慢。PGA/EPA随R增加而衰减的速度以坝坡最快，坝顶其次，坝基最慢。

3　峰值加速度的相关性分析

3.1同一测点记录的峰值加速度相关性分析

为了便于快速估计坝体地震响应的PGA及EPA值，采用下式进行PGA、EPA相关性分析[16]：

y=ax+b

(2)

式中，y、x可为PGA或EPA或它们的比值；a、b为回归方程的系数。

同一测点记录的相关性计算分析结果见表2。

从表2可以看出，PGA、EPA及其比值间均存在显著的线性相关性，相关系数的置信水平为99.9%；t值及回归方程F值的置信水平也在99.5%以上。利用相关性可进行PGA、EPA及其比值的预测。

3.2不同测点记录的峰值加速度相关性分析

坝顶和坝坡与坝基的PGA和EPA间存在强线性相关性，相关系数的置信水平均达到了99.9%；t值及回归方程F值的置信水平也达到了99.5%以上。其中，坝顶与坝基的东西分量PGA间的相关性强于坝坡与坝基的对应分量的相关性，水平南北和竖向分量的PGA则表现为坝坡与坝基的相关性强于坝顶与坝基间的相关性；坝顶与坝基间EPA的相关性强于坝坡与坝基间的相关性。抗震分析时，当已知坝基的PGA和EPA值时，可根据相关方程来推求坝顶及坝坡的相应值。

4　结论与讨论

通过对克孜尔大坝主坝0+180断面3个测点记录资料的分析得到如下主要结论：

(1)不同次地震，同一测点不同地震分量间PGA、EPA值差异显著。

(2)PGA和EPA随测点高度的变化规律基本相同，其中，测点高度对坝顶的地震响应影响显著，对坝坡地震响应的影响规律不一致。坝顶PGA和EPA均大于坝坡及坝基的对应值，坝顶具有较大的放大效应；坝坡跟坝基相比，不存在明显放大效应。

(3)同一测点相同地震分量间的PGA>EPA，且近场小震的PGA/EPA大于远场中强震的对应值。坝顶PGA与EPA值最为接近，坝坡的PGA值与EPA值的差异最大，PGA/EPA随测点高度变化的规律为先增后减。

(4)PGA及EPA均随M增加和R的减小而增加。近场小震的PGA/EPA随M和R增加而减小；远场中强震的竖向分量和坝顶及坝基的水平分量的PGA/EPA随M增加和R减小而增加，坝坡水平分量的PGA/EPA随M增加和R减小而减小。近场小震坝顶和坝坡的水平分量PGA大于坝基；坝顶和坝坡PGA随M增加而增加的速度快于坝基；EPA随M增加而增加的幅度坝顶大于坝基，坝坡与坝基相当；坝顶PGA/EPA值小于坝坡和坝基，随M增加而减小的幅度更小；坝坡PGA/EPA大于坝基，且随M增加而减小的幅度更大。PGA和EPA随R增加而衰减的速度以坝坡最快，坝基其次，坝顶最慢；PGA/EPA随R增加而衰减的速度以坝坡最快，坝顶其次，坝基最慢。

(5)同一测点的PGA与EPA、不同地震分量的PGA间以及EPA间均存在显著的线性相关性；坝顶和坝坡的PGA和EPA与坝基的PGA和EPA间存在强线性相关性。抗震分析时，当已知PGA、EPA相关对中的任一个量时，可以根据相关方程来预测另一量。

[1]新疆防御自然灾害研究所. 克孜尔水库地震危险性分析及对策[R]. 乌鲁木齐： 新疆防御自然灾害研究所， 1999．

[2]胡晓， 张艳红， 钟菊芳， 等. 中国重要大坝强震监测与地震动输入机制研究[R]. 北京： 中国水利水电科学研究院， 2006．

[3]胡聿贤. 地震工程学[M]. 第二版. 北京： 地震出版社. 2006．

[4]乔震元， 刘本玉， 张远富. 汶川8.0级地震峰值地震动特性研究[J]. 西北地震学报， 2011， 33(1)： 92- 95．

[5]陈鲲， 俞言祥， 高孟潭， 等. 2014年云南鲁甸Ms6. 5地震峰值加速度震动图[J]. 地震学报， 2015， 37(3)： 429- 436.

[6]陈厚群， 郭明珠. 重大工程场地设计地震动参数选择[C]∥中国水利水电科学研究院会议文集. 2002．

[7]姚凯, 孙崇绍, 朱珊珊， 等. 2008年汶川地震后的三次强余震地表峰值加速度衰减场研究[J]. 西北地震学报， 2012， 34(1)： 99- 103．

[8]李小军， 阎秀杰， 潘华. 中小震近场地震动估计中地震动衰减关系的适用性分析[J]. 地震工程与工程振动， 2005， 25(1)： 1- 7.

[9]朱勇华， 邰淑彩， 孙韫玉. 应用数理统计[M]. 武汉： 武汉水利电力大学出版社， 1999．

(责任编辑焦雪梅)

Analysis of the Characteristics of Dam Earthquake Records Peak Acceleration

ZHONG Jufang1, HU Xiao2, YANG Ronglai1

(1. College of Civil Engineering, Nanchang Hangkong University, Nanchang 330063, Jiangxi, China; 2. Earthquake Engineering Research Center, China Institute of Water Resources and Hydropower Research, Beijing 100044, China)

In view of the situation of instead of maximum peak ground acceleration (PGA) with effective peak acceleration (EPA) in earthquake engineering, the intrinsic correlation and statistical characteristics between EPA and PGA of dam seismic response are revealed by the data statistical analysis of earthquake monitoring array of Kezier Dam. The attenuation laws of EPA and PGA with the changes of seismic magnitude and epicenter distance are also revealed, and the influences of dam height on EPA and PGA are also explored. This study will provide theoretical basis and a practical model for the reasonable selection and forecast of peak acceleration in dam seismic calculation．

seismic record; maximum peak ground acceleration (PGA); effective peak acceleration (EPA); peak ratio; correlation

2015- 09- 09

国家自然科学基金项目(51468045)；科技部水利公益性行业科研专项项目(201401009)

钟菊芳(1972—)，女，江西龙南人，副教授，博士，研究方向为地震动输入机制．

TV64；TV312

A

0559- 9342(2016)05- 0020- 05