水力坡度变化下的降雨—出流试验研究

岑鑫雨，肖先煊，蔡国军，杨术刚，张家森，王　欣，黄宇彬

(1.成都理工大学环境与土木工程学院，四川成都610059；2.成都理工大学国家级地质工程实验教学示范中心，四川成都610059)



水力坡度变化下的降雨—出流试验研究

岑鑫雨1，2，肖先煊1，2，蔡国军1，2，杨术刚1，2，张家森1，2，王欣1，2，黄宇彬1，2

(1.成都理工大学环境与土木工程学院，四川成都610059；2.成都理工大学国家级地质工程实验教学示范中心，四川成都610059)

为探讨小流域出流对上游降雨的动态响应特征，在室内建立了潜水渗流地质模型，并开展了一定降雨条件下，水力坡度逐渐增大及水力坡度逐渐减小的小流域降雨-出流试验。结果发现，降雨条件不变，流域出流的峰值流量持续时间随水力坡度增大而减小，流量变化段的持续时间随水力坡度减小(增大)而增大(减小)；流域出流流量峰值会在降雨结束之前出现。分析认为地下径流的流域产、汇流模式对于降雨的响应较地表径流、壤中流与地下径流综合模式灵敏。研究为山前平原的地下水资源评价及陆面水体与地下水的水文过程的研究提供数据参考。

降雨；潜水；水力坡度；试验

0　引　言

在山前冲积平原、洪积扇及盆地，地势平坦，土壤肥沃，水量充沛，便于人类居住和从事相关生产活动。随着供水需求的增大、地表河流受到不同程度的污染，在现有的经济技术条件下，人类可利用的淡水资源越来越紧缺，故人们逐步将水源转向储量大、分布广、污染相对较小的地下水。但在生产生活中对地下水运动、分布等规律不够重视，导致因不合理开采利用地下水而产生的环境地质问题层出不穷：地面沉降、地裂缝等时刻困扰着当地居民的生产生活，所以充分认识地下水运动规律的任务更加紧迫。

纵观有关研究成果，张士锋等[1]认为：在降雨历时小于全面汇流时间和较小的降雨强度下，降雨历时与滞时有强烈的非线性关系。叶守泽等[2]持有：在充分降雨条件下，洪峰流量、降雨强度呈线性关系，降雨强度与峰现时间成负线性关系的观点。林三益等[3]指出：洪水过程受降雨过程和降雨量空间分布的影响灵敏，因此多呈现复峰过程，且涨落变化剧烈；即使是孤立单峰型洪水过程，其峰端也常在很短时间内出现骤落又猛涨的双峰或多峰，反映了与流域内降雨特性的密切关系。沈冰等[4- 7]在水文学一书中指出：在地表径流、壤中流与地下径流混合的流域产汇流模式中，流量过程的起始时刻、洪峰、重心等出现的时间均滞后于降雨过程。谢永玉[8]通过实验发现：在控制地下水埋深的条件下，次降雨入渗补给系数随地下水埋深的变化符合指数分布，在地下水位自由变动的条件下符合伽玛分布。

本试验则重点探讨潜水水力坡度变化下的降雨-出流效应。以某山前冲洪积平原为地质原型，在充分掌握该区域水文地质资料的基础上，在室内建立地质物理模型；并开展了一定降雨条件下，水力坡度逐渐增大及水力坡度逐渐减小的的小流域降雨-出流试验研究；为山前平原的地下水资源评价及陆面水体与地下水的水文过程的研究提供数据参考。

1　试验平台

1.1试验模型

以山前冲洪积平原为地质原型，在充分认识冲洪积平原的基本地质条件的基础上，根据相似原理，在室内建立了潜水渗流地质模型[9]，以模拟不同水力坡度下降雨-出流的动态过程。模型尺寸为194 cm×44 cm×156 cm，主要由渗流模拟箱，给、排水溢流箱，供水箱，排水箱，测压管组成。渗流模拟箱尺寸为151cm×30.5 cm×78 cm，箱内装有均质石英砂，模型靠近给水溢流箱一侧石英砂表面堆砌有卵石，面积约为600 cm2，厚度约为10 cm，以模拟冲洪积平原上游山区的地貌特征。

1.2试验参数及降雨条件

石英砂0.1～1 mm，卵石20～50 mm；石英砂重度γ=27 kN/m3；石英砂毛细上升高度hc=14.6 cm；石英砂渗透系数K=0.0453[9]。测流方法及精度控制：排水箱外接水管出水口处配有500 mL量筒，连续测流，每30 s测定一次出流流量并记录；若连续2次流量实测值相对误差小于3%，即(|Qn-Qn-1|/Q)≤3%时，表明出流流量稳定。本试验主要研究潜水面水力坡度对降雨出流的影响，应使模拟的降雨全部入渗，降雨强度的最大值等于降雨刚好能全部入渗而不致产生地表径流的雨强值。在准备实验时测得无降雨时流域中潜水的最小出流量为7.61 mL/s，故综合降雨模拟装置的参数及最大雨强值考虑，将降雨强度范围控制在2.50～3.00 mL/s符合试验的各项条件与要求；降雨模拟装置：本试验的降雨模拟装置主要由均匀带孔板(26 cm×24.5 cm)、给水溢流箱和水管组成，通过对给水溢流箱高度的调节控制均匀带孔板中水位高程恒定，此时降雨强度恒定；降雨条件：在卵石上方20 cm处，以降雨模拟装置模拟恒定雨强的大气降雨，每次实验总降雨量2 000 mL，降雨历时700 s，平均雨强为2.86 mL/s。

1.3试验过程

(1)水力坡度增大过程。第一次试验，供水箱与排水箱中水位相对高程分别为57.5 cm与39 cm，此时潜水面的水力坡度为0.12。待测流稳定后开始实验，用量筒在排水箱外接水管处测流，实验进行到10 min时，开始模拟降雨；45 min时，停止实验。将排水溢流箱的高度降低3 cm，待其流量稳定后重复第一次试验过程。此后，排水溢流箱的高度依次降低3 cm，总计开展7次试验，得到不同水力坡度下流量值随时间的变化关系(见图1)。

(2)水力坡度减小过程。上述试验过程完成后，排水箱水位相对高程为24 cm，设定此高程为排水箱中水位上升的初始值。在此高程基础上，以3 cm/次的高度依次提升排水箱中的水位，重复水力坡度增大时的试验过程，直至排水箱水位高程提升至39 cm。试验过程2结束后，得到7组不同水力坡度下流量值随时间的变化关系(如图2)。

2　结果分析

2.1流量随时间的变化关系曲线

水力坡度增大及减小过程的Q-t曲线见图1～2。

图1　水力坡度增大过程Q-t曲线(图中●表示起涨时刻，▲表示峰值时刻，■表示退涨时刻)

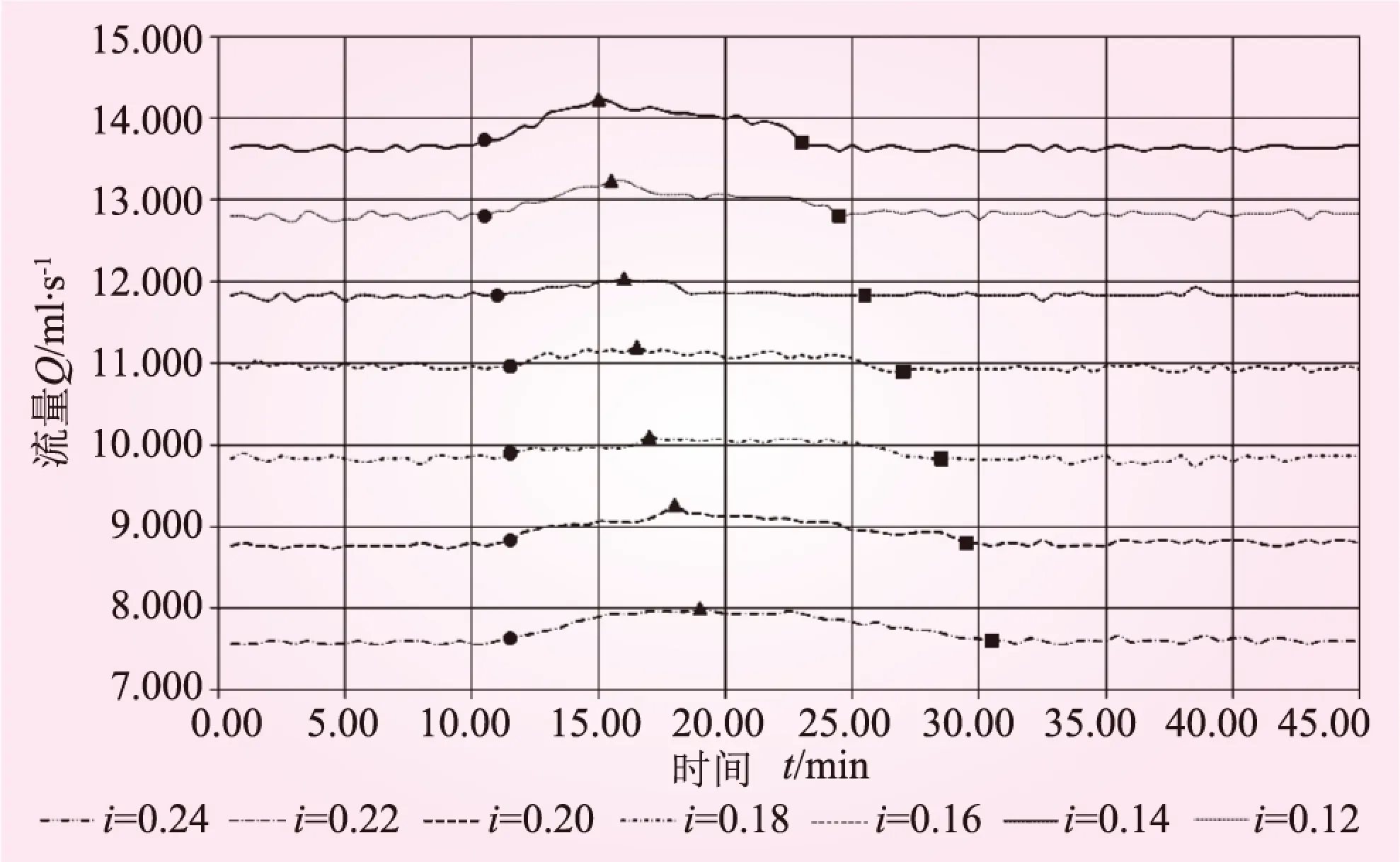
图2　水力坡度减小过程Q-t曲线(图中●表示起涨时刻，▲表示峰值时刻，■表示退涨时刻)

从图1中可以看出，下游出流量在上游产生降雨后呈现出先增大后减小直至稳定的整体趋势，每一条Q-t曲线都能明显的分为三个阶段：降雨前与退涨点后的流量稳定段、流量起涨段和流量退涨段，令流量起涨段时间为T1，流量退涨段时间为T2。由图可知：流量值随水力坡度i的增大而增大；水力坡度相等时，水力坡度增大过程中的流量大于水力坡度减小过程；降雨前的稳定流量与退涨后的流量相等；流量峰值点出现在降雨过程结束之前；在同一Q-t图中，降雨后流量起涨的时间基本一致，T1与T2随水力坡度i的增大而减小；对比图1和图2发现，水力坡度减小(图1)过程中的流量峰值点较水力坡度增大(图2)过程中前移，在两图流量起涨点位置基本相同的前提下，可知当水力坡度相等时，水力坡度增大过程中的T1大于水力坡度减小过程。

2.2流量与水力坡度关系

通过对水力坡度增大和减小两个过程的对比分析，得出峰值流量、稳定流量与水力坡度i的关系见表1。具体分析如下：

表1流量与水力坡度的关系

水力坡度减小水力坡度增大iQ1/mL·s-1Q2/mL·s-1Q2-Q1/mL·s-1iQ1/mL·s-1Q2/mL·s-1Q2-Q1/mL·s-10.127.618.000.390.128.058.670.520.148.749.270.530.149.179.800.630.169.8310.100.270.1610.2811.000.720.1810.9111.200.290.1811.2412.230.990.2011.8412.030.190.2012.2413.000.760.2212.7613.230.470.2213.0413.500.460.2413.7014.230.530.2413.9014.670.77

(1) 流量随水力坡度的变化分析。由表1可知：峰值流量与稳定流量随着水力坡度的增大(减小)而增大(减小)；水力坡度相同时，水力坡度增大阶段的流量以及峰值流量与稳定流量的差值均明显大于水力坡度减小阶段。水力坡度每增大(减小)0.02，峰值流量增大(减小)0.67～1.27 mL/s，平均变化率为8.56%，稳定流量增大(减小)0.80～1.13 mL/s，平均变化率为9.07%；水力坡度i增大过程中的稳定流量较i减小过程增加0.21～0.45 mL/s，平均增加率为3.34%；水力坡度i增大过程中的峰值流量较i减小过程增加0.34～0.83 mL/s，平均增加率为5.72%；同一次试验中，峰值流量较稳定流量增大0.6～1.0 mL/s，平均增加率为5.67%；试验时，通过调节稳定流排水系统的高程来降低出流断面的潜水位高程，在上游潜水位高程恒定的前提下，达到改变潜水水力坡度的目的。故在水力坡度增大的过程中，下游潜水位的高程是不断下降的，当潜水位下降时，水压力p减小，根据Terzaghi有效应力公式[10]σ=σ′+p。式中，σ为多孔介质总应力；σ′为有效应力；p为孔隙水压力。当水压力p减小时：地下水体积膨胀，从而释放出一部分地下水；地下水对上覆岩土体浮力降低，为维持平衡，这部分力将转嫁到多孔介质固体骨架上，有效应力σ′增大，压缩多孔介质(固体+空隙)，结果使含水层空隙度n变小、介质挤密、厚度变薄，挤压孔隙释放一部分地下水。释放出的地下水垂向补给下部含水层，使得下部含水层在垂向水流的补给下，赋存更多的地下水，而这部分补给的水流同含水层中原始所含水量在水头差与上游降雨入渗的地下径流的驱动下，流出流域，导致流域出流量增加且流量值波动幅度较大。故当水力坡度相同时，水力坡度增大过程中的出流量以及峰值流量与稳定流量的差值大于水力坡度减小过程。

(2)流量峰值点的动态分析。由图1、2可知，流量峰值点都出现在降雨过程完成前。已知当降雨形成河川径流时，流量过程的起始时刻、洪峰、重心等出现的时间均滞后于降雨过程[4- 7]，在本试验中，降雨全部入渗形成地下径流，流量过程的峰值出现时间提前于降雨过程。将本试验的流量过程与河川径流的形成过程对比(见图3)，两者都有明显的产流与汇流过程。本试验中产流过程就是模拟的大气降雨在垂直方向上的入渗过程，而河川径流的产流过程是大气降雨到达地面后，经过植物截留、填洼及地面蓄水、土壤蓄水、地下水蓄存和深层地下水的储存，从而形成地面径流、壤中流和地下径流的过程[4]。本试验的汇流过程是入渗至石英砂的降雨，在潜水水力坡度的作用下，横向运移至仪器出流断面的过程，由于本试验的介质是均质石英砂，在试验仪器中只存在着潜水含水层，故在地下水的汇流过程中只存在着地下径流这一种汇流模式；在河川汇流中，汇流过程分为坡地汇流和河网汇流，其中在河网汇流过程中，形成了地表径流、壤中流、浅层地下径流与深层地下径流，汇流模式较本试验复杂。此外，由于本试验中降雨全部入渗形成浅层地下径流，且只有单一的地下径流汇流模式，流量过程曲线中的流量峰值点都出现在降雨过程完成前，说明在降雨结束前，流域下游出口流量已达到峰值；在河川径流降雨—出流示意图中，流量过程的起始时刻、洪峰、重心等出现的时间均滞后于降雨过程，这是由于坡面漫流、壤中流和地下径流汇集到出口断面所需时间不同，因而在图3中，各类径流终止时间不同，且直接降落在河槽水面上的雨水所形成的径流最先终止，然后依次是地表径流、壤中流、浅层地下径流，最后是深层地下径流[4]。

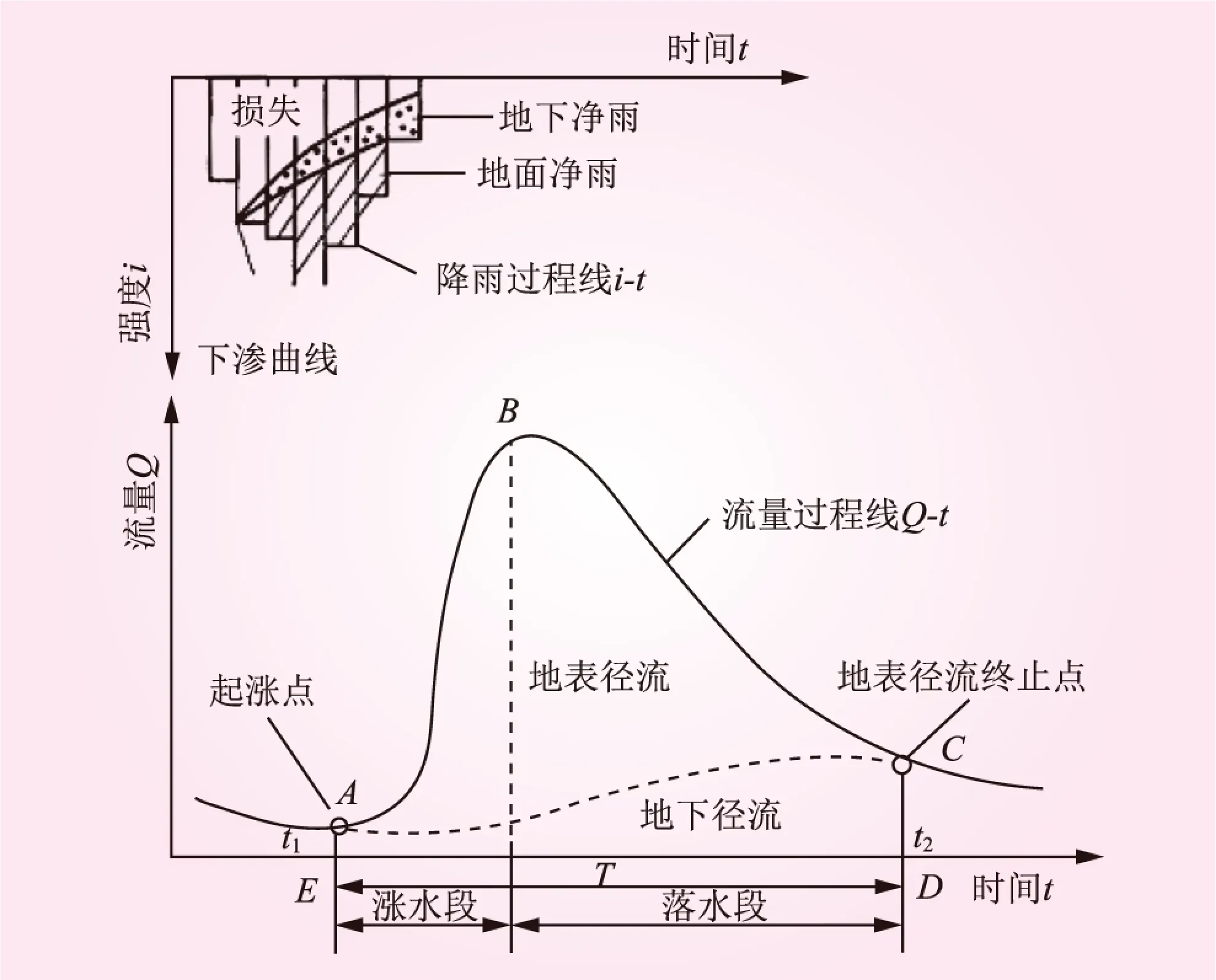
图3　河川径流一次降雨径流过程示意 [4]

2.3流量涨、退时间与水力坡度关系

通过对图1、图2流量变化过程的统计分析，得出降雨开始到峰值出现的时间段T1、达到峰值流量至流量稳定的时间段T2与水力坡度i的关系(见表2)。

表2T1、T2与水力坡度i的关系

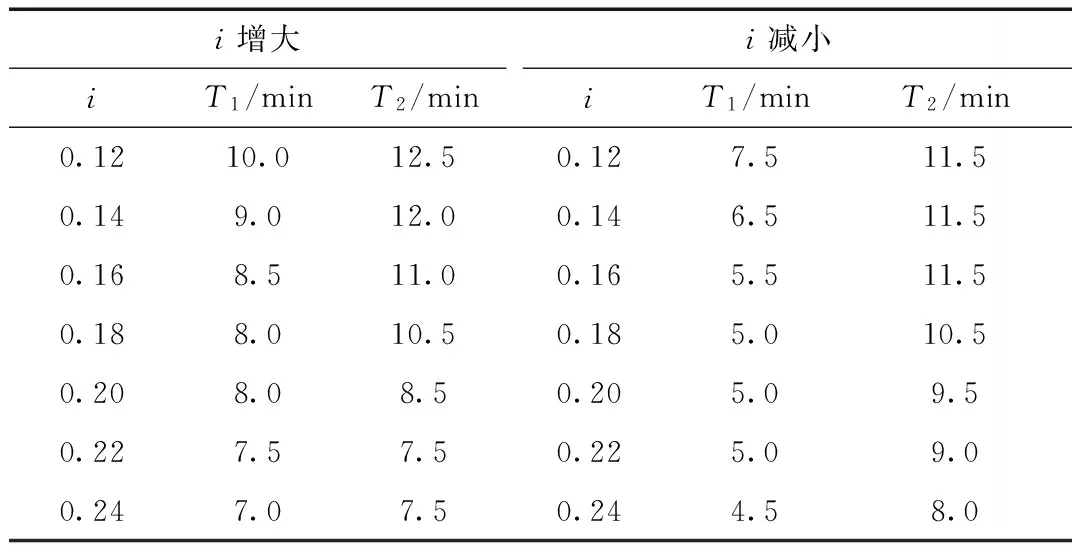
i增大i减小iT1/minT2/miniT1/minT2/min0.1210.012.50.127.511.50.149.012.00.146.511.50.168.511.00.165.511.50.188.010.50.185.010.50.208.08.50.205.09.50.227.57.50.225.09.00.247.07.50.244.58.0

(1)T流量非稳定段时间随水力坡度变化规律。T=T1+T2，T均随水力坡度i的增大而减小。根据达西定律Q=KA(H1-H2)/L=KAi。式中，Q为渗透流量；A为过水断面面积；H1、H2分别为上、下游过水断面的水头；L为上下游过水断面间距离；K为渗透系数。本试验中，渗透系数K恒定，过水断面面积变化很小故视为不变，可知水力坡度i增大时，根据达西定律计算所得的渗透流量Q也增大。由于本试验降水量恒定，故当出流流量增大时，总降水量出流所需时间减短，故在水力坡度增大与减小两个过程中，都呈现出T随水力坡度i的增大而减小的规律。

(2)水力坡度相同时T1与T2分析。由表2所示，当水力坡度相同时，T2大于T1，流量退涨段用时较流量增加段长。在流域产流中，地下径流的形成有4个前提条件：要有界面，即包气带的下界面，实际上就是潜水面；要有供水fc，且fc强度大于下层下渗强度fB；界面上产生积水，形成临时饱和带(相对起始潜水面而言)；具备一定的坡度[11]。可知当降水下渗至潜水面时，形成了一个高于原始潜水面的临时饱和带，降雨结束(即入渗水量减少)后，临时饱和带中的水释放，饱和带随之消失。故在流量增加的过程中，临时饱和带起到了给出水量的作用，而在流量减少的过程中，饱和带由于降雨入渗结束而消失，造成水力坡度相同时，T2大于T1(见图4)。

图4

由图4可知，水力坡度增大T1-i曲线整体位于水力坡度减小阶段之上，说明在水力坡度增大过程中T1整体大于水力坡度减小过程。造成此现象的原因也可用上述Terzaghi有效应力公式解释。即，由于水压力p的减小，含水层中释放出了更多的水量，故当水力坡度(图4中横坐标)相同时，水力坡度增大过程的T1大于水力坡度减小过程。同时也可从图4中得出，无论水力坡度处在增大或减小的过程，曲线的斜率基本一致，则T1随i变化时的变化率是大致相同的。

由图4可知，T2-i两条曲线的相交点为(0.18，10.5)，当水力坡度小于0.18时，水力坡度增大过程的T2大于水力坡度减小过程，反之，当水力坡度大于0.18时，水力坡度增大过程的T2小于水力坡度减小过程。水力坡度增大过程大于水力坡度减小过程，说明在水力坡度增大过程中，T2随i变化时的变化率大于水力坡度减小过程。即水力坡度的增大对地下径流流量退涨时间的影响大于水力坡度的减小对其的影响。当降雨在季节上分配不均，存在着明显的丰水期与枯水期时，丰水期时降雨丰沛，地下潜水位抬升；枯水期时降雨量少，地下潜水位下降，分别对应了本试验中的水力坡度减小过程与水力坡度增大过程。因此，在实际的生产生活中预测一次降水形成的河川径流流量退涨过程对地下径流进行分析时，应考虑该区域当时地下潜水面所处的变化阶段对流量出流的影响。

3　结　论

(1)根据Terzaghi有效应力原理，水压力的减小导致含水层水量的释放，i相同时：增加过程的稳定流量与峰值流量均大于i减小过程，增加率分别为3.34%与5.72%；且i增大过程的T1大于i减小过程，将T1理解为地下径流峰值流量与降雨的滞时，则可得当降雨完全入渗时，除流域面积、介质类型等影响因素外，潜水的初始水力坡度也是影响降雨出流滞时的因素之一。

(2)降雨全部入渗时，流量过程的峰值出现时间提前于降雨过程。可推知，只有地下径流的流域产、汇流模式对于降雨的响应较地表径流、壤中流与地下径流综合模式更加灵敏。

(3)根据达西定律，渗透系数K与过水断面面积A恒定时，流量Q随水力坡度i的增大而线性增大，而流域降水量一定，则流量非稳定段时间T随水力坡度i的增大而减小。

(4)由于降雨入渗形成高于潜水面的临时饱和带，当i相同时，T2大于T1，流量退涨段用时较流量增加段长。

(5)i的增大对地下径流流量退涨时间T2的影响大于i的减小对其的影响，故预测一次降水形成的河川径流流量退涨过程，对地下径流进行分析时应考虑该区域当时地下潜水面所处的变化阶段对流量出流的影响。

[1]张士锋， 刘昌明， 夏军， 等. 降雨径流过程驱动因子的室内模拟实验研究[J]. 中国科学： D辑地球科学， 2004， 34(3)： 280- 289．

[2]叶守泽， 陈绳甲. 由暴雨推求洪水的非线性处理方法[J]. 武汉水利电力学院学报， 1978(1)： 25- 40．

[3]林三益， 易立群. 四川省山区河流降雨洪水特性及防治对策[J]. 四川水利发电， 1998， 17(2)： 8- 15．

[4]沈冰， 黄红虎， 薛焱森. 水文学原理[M]. 北京： 中国水利水电出版社， 2008．

[5]WOOLHISER D A, LIGGETT I A， Unsteady one-dimensional flow over a plane-the rising hydrograph[J]. Water Resources Research， 1967， 3(3): 753- 771．

[6]EAGLESON P S. Dynamic hydrology[M]. New York： Mc-Graw-Hill Book Company， 1970．

[7]PINDER G F, GRAY W G. Finite element simulation in surface and subsurface hydrology[M]. NewYork： Academic Press Inc， 1977．

[8]谢永玉. 淮北平原降雨入渗补给系数随地下水埋深变化特征[J]. 地下水， 2012， 34(1)： 10- 11．

[9]肖先煊， 许模， 蔡国军， 等. 基于潜水渗流模型的地下水实际流速[J]. 实验室研究与探索， 2013， 32(4)： 11- 14．

[10]薛禹群， 吴吉春. 地下水动力学[M]. 北京： 地质出版社， 2010．

[11]于维忠. 论流域产流[J]. 水利学报， 1985， 2(2)： 1- 11．

(责任编辑陈萍)

Experimental Study on Rainfall and Discharge under the Change of Hydraulic Gradient

CEN Xinyu1,2, XIAO Xianxuan1,2, CAI Guojun1,2, YANG Shugang1,2, ZHANG Jiasen1,2, WANG Xin1,2, HUANG Yubin1,2

(1. College of Environment and Civil Engineering, Chengdu University of Technology, Chengdu 610059, Sichuan, China;2. National Geological Engineering Experimental Teaching Demonstration Center of Chengdu University of Technology, Chengdu 610059, Sichuan, China)

In order to study the dynamic response characteristics of runoff to the rainfall in upper reaches of small watershed, a indoor geological model of water flow is established, and a series of experiments of rainfall-flow under the conditions of gradual increasing and decreasing of hydraulic gradient and the condition of certain rainfall are conducted respectively. The test results show that: (a) when the rainfall condition is constant, the duration of peak flow of drainage basin will decrease with the increase of hydraulic gradient, and the duration of flow rate variation will correspondingly decrease or increase with the increase or decrease of hydraulic gradient; and (b) the peak discharge of basin will appear before the end of rain. The analyses believe the flow pattern of underground runoff of river basin responses more sensitive to the rainfall than the patterns of surface runoff and integrated interflow and underground runoff. This study can provide data reference for groundwater resources evaluation and hydrological process research of surface water and groundwater of piedmont plain.

rainfall; phreatic water; hydraulic gradient; experiment

2015- 06- 16

国家重点实验室人才培养项目(SKLGP2014Z014)；四川省教育厅基金项目(11ZB038)以及成都理工大学中青年骨干教师培养计划

岑鑫雨(1994—)，女，四川乐山人，从事地下水科学与工程专业学习研究．

TV121.1

A

0559- 9342(2016)05- 0007- 05