某机载雷达天线框架结构的有限元分析*

吴文志，胡劲松，宋 敏

(1. 中国电子科技集团公司第三十八研究所， 安徽 合肥 230088；2. 国家级工业设计中心， 安徽 合肥 230088)

某机载雷达天线框架结构的有限元分析*

吴文志1,2，胡劲松1，宋 敏1

(1. 中国电子科技集团公司第三十八研究所， 安徽 合肥 230088；2. 国家级工业设计中心， 安徽 合肥 230088)

天线框架是天线的安装平台和精度基准，其结构刚度与强度直接关系到机载雷达的性能。文中以某机载雷达天线框架结构为研究对象，建立了完整的有限元仿真模型，进行了模态分析，给出了结构的前6阶固有频率及振型，完成了该结构在加速度过载下的准静态分析及随机振动的响应分析，得到了相应的变形和应力值，并计算了相应的安全裕度。结果表明，该机载雷达天线框架具有较高的基频和较好的刚强度，结构设计满足机载产品抗力学环境设计要求。

天线框架；有限元分析；模态分析；加速度过载；随机振动

引 言

相比于地面雷达，机载雷达以飞机为载体，具有可视距离远、警戒时间长、结构紧凑、重量轻、可靠性高等显著优点，在现代战争中得到了广泛的应用。机载雷达结构在运输、工作等各个阶段，经常经受飞机的起飞、着陆、滑行及外部扰流等因素产生的加速度、噪声、冲击、振动等各种复杂、严苛的动力学环境。动力学载荷会引起天线结构的变形，甚至严重破坏天线的本体结构，对天线的电性能产生严重影响。因此，动力学环境对机载雷达天线结构的安全性和可靠性的影响不容忽视，已引起广泛的研究兴趣[1-6]。

随着计算机技术的进步和计算机辅助工程(CAE)技术的迅速发展，动力学环境对结构力学性能的影响已可通过有限元仿真技术进行计算机模拟。通过仿真分析，评估结构的抗力学环境设计，暴露结构设计的薄弱环节，提高结构的安全性和可靠性。

天线框架是支撑天线探测目标的装置，作为整个机载雷达天线系统的主承力件，既要保证天线结构在恶劣动力学载荷作用下不产生损伤乃至破坏，又要确保天线的工作性能得到最大程度的发挥，因此天线框架需具有较好的刚强度和动态特性。对天线框架在给定的外部激励下的响应进行系统的有限元分析对其结构设计有着重要的指导意义。

本文主要研究了动力学环境对机载雷达天线力学性能的影响。结合某机载雷达天线框架精确的三维模型，建立了相应的有限元仿真模型，完成了结构的模态分析、加速度过载下的准静态分析以及随机振动的响应分析。结果表明，该机载雷达天线框架的结构设计满足机载产品抗力学环境设计要求。

1 机载雷达天线框架结构

该机载雷达天线框架为薄壁空腔结构。为了便于内部设备的安装和维护，上下侧壁共开有4 组方孔，该电子设备的三维模型如图1所示，整个设备通过10个螺栓连接于飞机平台上。

图1 机载天线框架的三维结构示意图

2 机载天线框架结构有限元模型的建立

2.1 网格划分和边界条件

进行有限元计算时，需将结构离散成等价的有限单元系统，即网格划分。本文根据该机载天线框架结构的特点，对框架的一些细节方面做了适当的简化。忽略小孔、圆角、倒角等结构细节。模型采用壳单元模拟。整个有限元模型共有252 124个单元。机载天线框架结构的有限元计算模型如图2 所示。其中X方向为飞机航向，Y方向为垂向，Z方向为飞机侧向。计算时，10个安装孔位置完全固定。

图2 机载天线框架结构的有限元模型

2.2 材料参数

该天线框架结构所用的材料均为铝合金5A06，其杨氏模量为70 GPa，泊松比为0.33，密度为2 700 kg/m3，屈服强度为155 MPa。

2.3 力学环境条件

根据机载产品抗力学环境设计的要求，该结构需承受的载荷有加速度过载、随机振动等。进行结构设计时，需确保在上述力学环境作用下，该结构不会被破坏。

该机载天线框架结构所对应的加速度过载试验条件见表1。

表1 机载天线框架结构加速度过载试验条件

随机振动试验振动谱如图3所示。其中L1取0.3g2/Hz，L2取0.075 4g2/Hz，L3取0.033 6g2/Hz，L4取0.018 9g2/Hz；F1取107.5 Hz，F2取215 Hz，F3取322.5 Hz，F4取430 Hz，尖峰带宽为中心频率的±5%。试验轴向为X、Y、Z三个轴向。试验时间为每个轴向1 h。

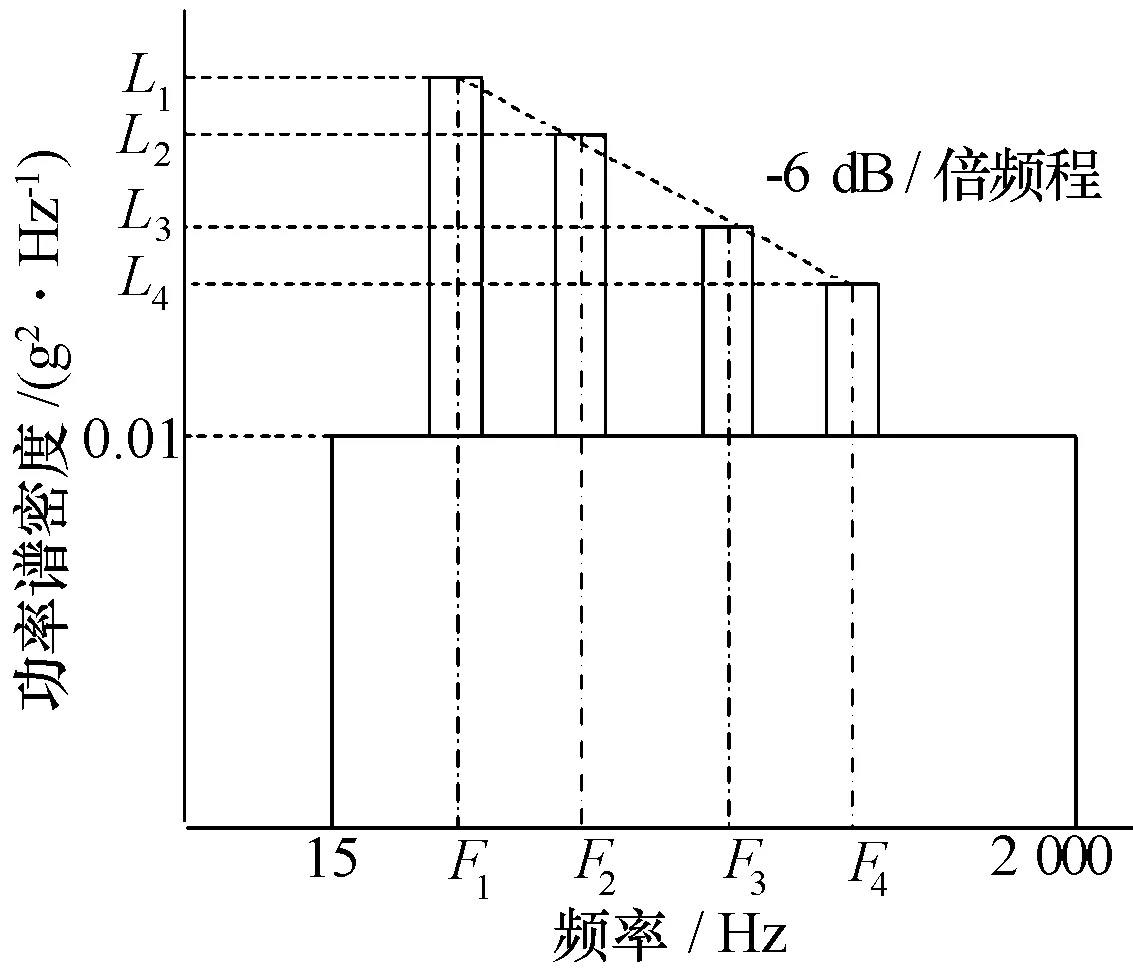
图3 机载天线框架随机振动试验条件

3 机载天线框架结构有限元分析结果

本文根据机载天线框架结构所经受的动力学环境，完成了模态计算、加速度过载以及随机振动分析，计算结果如下。

3.1 机载天线框架结构模态分析

模态分析的目的是识别出系统的模态参数[7]，得到结构固有的动态特性，包括固有频率、模态振型和阻尼比等，找出结构的薄弱环节，为结构系统的振动分析、振动故障诊断和预报、结构动力特性的优化设计提供依据。本文采用振型叠加法，使用Lanczos法提取特征值，计算该天线框架结构的固有频率及相应的振型。

该框架结构在约束态下的前6阶固有频率见表2，振型如图4所示。

表2 机载天线框架结构前6阶固有频率

由表2可知，该天线框架的前6阶固有频率较高，频率均大于430 Hz，有效地避开了外界激励力的频率，避免了共振现象的发生。由图4可知，约束模态下，前5阶模态对应的振型为天线框架侧壁的弯曲变形，这主要是由于侧壁刚度较差，是该天线框架较为薄弱的部位。第6阶模态振型的振幅最大点位于与飞机平台相连的侧板上。

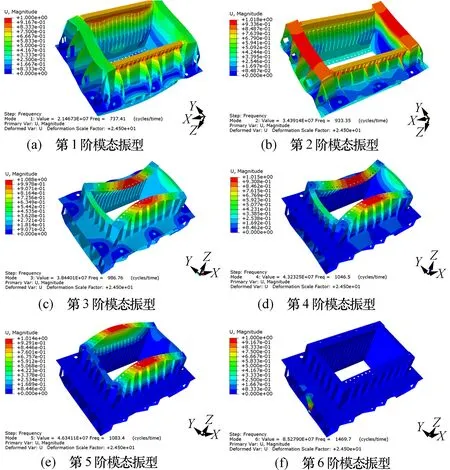
图4 机载天线框架结构前6阶模态振型图

4 机载天线框架结构加速度过载分析

加速度过载是机载设备在工作过程中需承受的重要的动力学环境之一。该天线框架结构对应的加速度过载试验条件见表1。加速度激励载荷按给定的大小沿不同方向分别施加在整个结构上。由于加速度激励载荷维持时间较长，而且其变化符合线性规律，因此可将加速度过载看成一个近似准稳态过程，分析时直接采用静力分析的方法进行[8-9]。考虑到结构所用材料的应力-应变关系及应变-位移关系均为线性的，本静力分析为线性静力分析，因此，本文仅给出向后4.5g、向上6.75g和向左3g的计算结果，应力和变形分布云图如图5所示，计算数值见表3。

图5 加速度过载下机载天线框架结构刚强度响应

由图5可知，X轴向施加4.5g的加速度激励载荷时，结构的最大变形1.42e-3 mm，位于框架边缘处，最大应力为1.67 MPa，位于结构安装孔处；Y轴向施加6.75g的加速度激励载荷时，结构的最大变形3.19 e-3 mm，位于框架边缘处，最大应力为9.35 MPa，位于设备与框架的刚性连接处；Z轴向施加3g的加速度激励载荷时，结构的最大变形9.06e-4 mm，位于框架边缘处，最大应力为2.73 MPa，位于框架边缘处。结构变形及应力水平均满足抗力学环境设计要求。

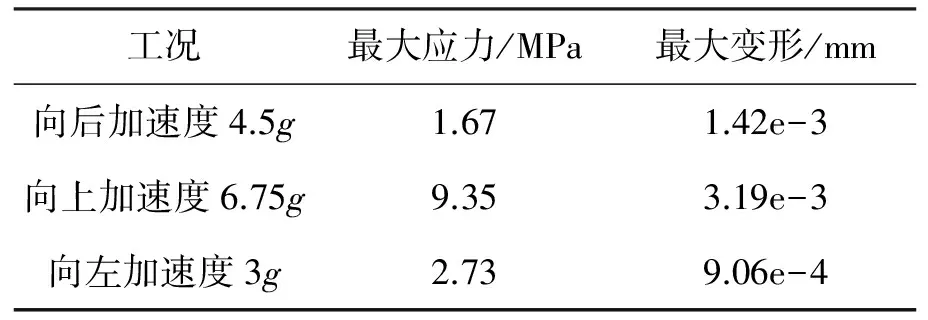
表3 加速度过载作用下天线框架的计算数值

5 机载天线框架结构随机振动仿真分析

当结构所受振动是连续的，并且可以使用功率谱密度(PSD)函数来表达作用荷载时，该结构在随机振动作用下的线性响应可以通过模态叠加原理的方法计算得到。

通过模态分析可知，该天线框架的前13阶固有频率位于0～2000 Hz以内，提取相应的固有频率及振型后，采用振型叠加法，取结构阻尼比0.03，研究该天线框架结构随机激励的线性响应。

施加轴向基础激励后系统的1σ应力和1σ变形分布云图，如图6所示。从分析结果可知，在X向随机载荷作用下，结构的最大1σ应力(不出现大于此值的概率0.682)为6.45 MPa，最大1σ变形为5.07e-3 mm，位于框架边缘处；在Y向随机载荷作用下，结构的最大1σ应力为21.4 MPa，最大1σ变形为7.03e-3 mm，位于框架边缘处；在Z向随机载荷作用下，结构的最大1σ应力为13.88 MPa，最大1σ变形为5.44e-3 mm，亦位于框架边缘处。

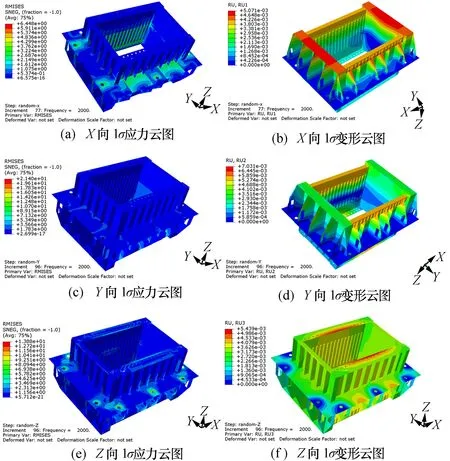
图6 随机振动下机载天线框架结构的刚强度响应

施加轴向随机振动激励后系统对应的3σ应力和3σ变形见表4。在X、Y、Z向随机载荷作用下，结构的最大3σ应力(不出现大于此值的概率为0.997)分别为19.4 MPa、64.2 MPa和41.6 MPa，结构的最大3σ变形分别为1.52e-2 mm、2.11e-2 mm及1.63e-2 mm。

表4 随机振动下天线框加3σ变形和应力计算数值

综合1σ变形、1σ应力、3σ变形及3σ应力分析结果可知，在Y向随机载荷激励下，结构的变形及应力水平明显大于沿X向或Z向，这是由于该机载天线框架在Y向的刚度较弱。为评估结构的抗力学环境设计效果，定义安全裕度：

其中,σs为材料的许用破坏应力;σSGE为等效使用应力;f为安全系数，视不同的材料选取合适的量值，一般取1.5。在Y向随机振动激励下，结构的安全裕度为MS ≥ 0.61 > 0，结构设计满足抗力学环境设计要求。

6 结束语

本文以某机载雷达天线框架结构为对象，研究了动力学环境载荷对其刚强度的影响。完成了该结构的模态计算、加速度过载下的准静态分析以及随机振动分析。有限元分析给出了框架结构的前6阶固有频率与模态振型、加速度过载下的框架应力和变形云图以及随机振动条件下的框架结构强度、刚度响应和安全裕度。研究结果表明该天线框架的结构设计满足机载产品抗力学环境的设计要求。

[1] 王志刚, 王志海. 某机载SAR天线支架的结构设计与分析[J]. 机械与电子, 2011(6): 16-18.

[2] 朱志远. 机载雷达框架刚强度分析[J]. 机械与电子, 2009(5): 65-67.

[3] 朱春临, 左防震. 某机载雷达柱式天线框架的研制[J]. 航空制造技术, 2013(10): 84-87.

[4] 任开锋, 李凤英, 宋志行, 等. 某机载雷达相控阵天线结构设计[J]. 电子机械工程, 2010, 26(2): 43-46.

[5] 宋志行, 关宏山, 钱海涛, 等. 机载有源相控阵天线的结构设计[J]. 雷达科学与技术, 2005, 3(3): 189-192.

[6] 顾吉丰. 机载雷达驱动机构的刚度分析计算[J]. 现代雷达, 2001, 23(3): 69-70, 86.

[7] 范文杰. 星载电子设备宽频随机振动响应分析[J]. 电子机械工程, 2010, 26(4): 5-8.

[8] 吴文志, 程林, 张平, 等. 某星载雷达电子设备的刚强度有限元分析[J]. 电子机械工程, 2016, 32(3): 56-59.

[9] 吴文志, 彭超, 张平, 等. 星载波导裂缝天线的动态响应特性研究[J]. 机械与电子, 2016(2): 35-37.

吴文志(1984-)，男，博士，工程师，主要从事军用电子设备结构力学仿真分析。

Finite Element Analysis of the Antenna Frame Structure of an Airborne Radar

WU Wen-zhi1,2，HU Jin-song1，SONG Min1

(1.The38thResearchInstituteofCETC,Hefei230088,China； 2.NationalIndustrialDesignCenter,Hefei230088,China)

The antenna frame is the installation platform and precision benchmark of airborne radar antenna. The stiffness and strength of the electronic equipment effect on the performances of airborne radar crucially. In this paper, the stiffness and strength response analysis of the antenna frame structure of an airborne radar is established. Based on the precise FEA model, the modal analysis is conducted; the natural frequency and vibration modes are obtained. Then the quasi-static analysis of the acceleration overload is carried out and the values of deformation and stress are obtained. The random vibration performance is also analyzed and the corresponding mechanical responses are obtained. It is shown that the structure design of the antenna frame structure of the airborne radar satisfies the strength requirement.

antenna frame; finite element analysis; modal analysis; acceleration overload; random vibration

2016-09-14

V474.2

A

1008-5300(2016)06-0052-04