一种可伸缩充压管驱动元件及其应用研究*

张 平

(1. 中国电子科技集团公司第三十八研究所， 安徽 合肥 230088；2. 国家级工业设计中心， 安徽 合肥 230088)

一种可伸缩充压管驱动元件及其应用研究*

张 平1，2

(1. 中国电子科技集团公司第三十八研究所， 安徽 合肥 230088；2. 国家级工业设计中心， 安徽 合肥 230088)

自适应技术被认为是提高传感器飞行器续航能力的有效途径之一，而驱动器是自适应结构可以实施的保障。文中提出了一种“驱动件即结构件”的可伸缩充压管驱动元件，具有驱动和承载双重作用。建立了可伸缩充压管的力学模型并推导得到等效刚度的简化公式。将充压管驱动器应用到某自适应机翼结构中，对机翼在气流扰动下的振动变形进行了仿真。结果表明可伸缩充压管可以产生足够的驱动力和驱动位移，同时可以为自适应结构提供有效的刚度支撑。

传感器飞行器；自适应技术；可伸缩充压管

引 言

自适应技术可以实现翼型弯度、厚度等重要参数的实时调节，提高飞行器整个飞行包线内的气动效率，在先进传感器飞行器中有着重要的应用前景[1-3]。而驱动装置是自适应变形的保障，研究人员普遍认为适合自适应结构的驱动器需要满足重量轻、可以提供较大的驱动力和位移等要求[4-5]。

传统的驱动方法有液压、电机驱动等[6-7]，液压驱动可以输出较大的力和位移，但是作动筒重量大；电机驱动结构重量较小，但是功率体积比不高且工作可靠性有待加强。近年来，新式驱动器如压电堆积、超声电机、SMA驱动器得到了广泛研究，压电驱动结构轻、驱动力大[8]，但是驱动位移小，将压电效应与机械振动结合的超声电机克服了驱动位移不足的缺点，目前在很多领域得到了应用，还需解决输出功率小以及使用寿命短等问题。SMA驱动具备较高的输出功率体积比[9]，由于材料对温度敏感，实际环境下不易控制。

综合考虑驱动效率、变形控制以及驱动力和位移，传统液压驱动在自适应机翼设计中仍然具有工程应用空间。尤其对于尺寸较大的无人飞行器，一般自带液压源，只要能够控制驱动元件的重量，对整个飞行器附加重量的影响是可以接受的。而常规的集中式刚性液压作动筒的重量显然难以满足要求。

本文通过结构灵巧设计，提出了一种“驱动件即结构件”的可伸缩充压管，具有重量轻、可输出较大驱动力和位移的特点。此外，该驱动元件还可以提供轴向刚度，用在自适应机翼上，可以抵抗可变形结构的振动变形。给出了该可伸缩充压管的结构方案和工作原理，建立了其等效刚度分析模型，并推导了等效轴向刚度的计算公式。将该可伸缩充压管阵列应用于某后缘变弯度机翼中并对后者的变形效果进行了仿真，结果显示该可伸缩充压管可以产生足够的驱动变形，同时可以有效地抑制机翼后缘在气流中的振动变形。

1 可伸缩充压管结构方案

可伸缩充压管方案如图1所示，单个充压管组成包括橡胶管芯、铝合金内/外套管、管口阀芯等。多个充压管可以通过阀芯与连接器相连，实现并联和串联分布。

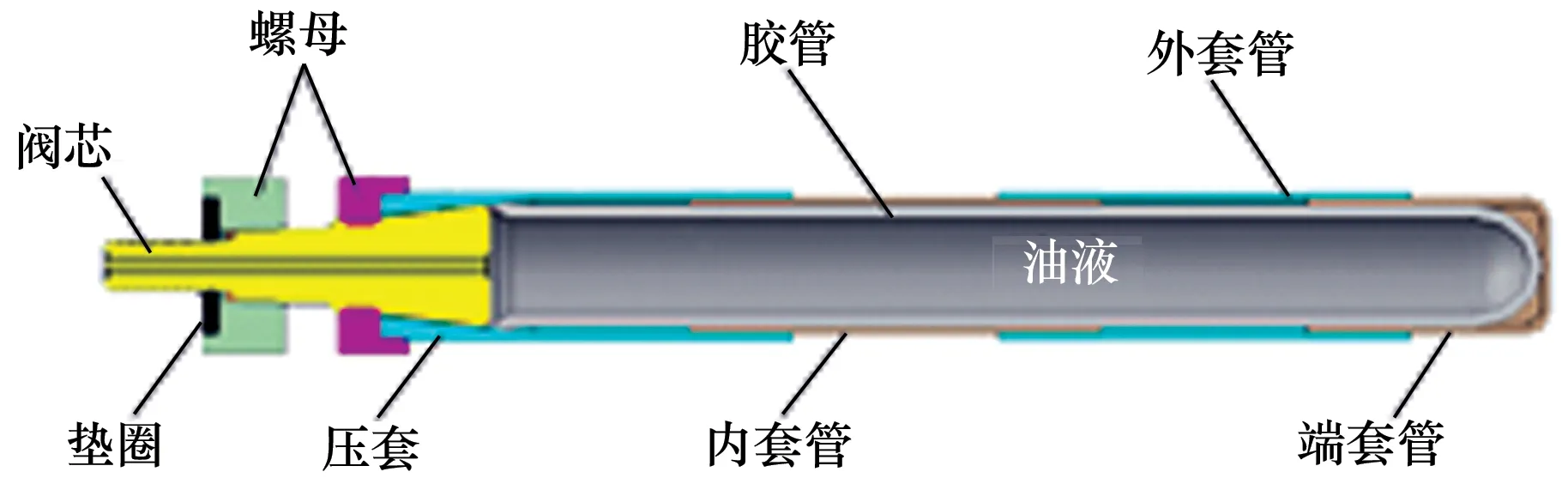
图1 可伸缩充压管结构示意图

当胶管内增压后，由于铝合金套管限制了胶管的径向膨胀，胶管只能沿着轴向变形，带动铝合金套管滑动变形，使得整个充压管产生伸长变形。为了实现双向驱动变形，可以在胶管内预先充有一定的油压，使得管长由自然长度达到工作初始长度，在工作初始长度下，通过加压或减压可以实现充压管双向约10%的变形量。

2 充压管等效刚度模型及分析

2.1 等效刚度模型

对可伸缩充压管进行建模，如图2所示，包括液柱、胶管壁和刚性套管壁3层。主要参数包括油液有效体积模量βe，套管壁厚ts，胶管的拉伸模量Et、压缩模量Ec，泊松比ν。在自然状态下胶管长L0，壁厚t0，内径为d0。

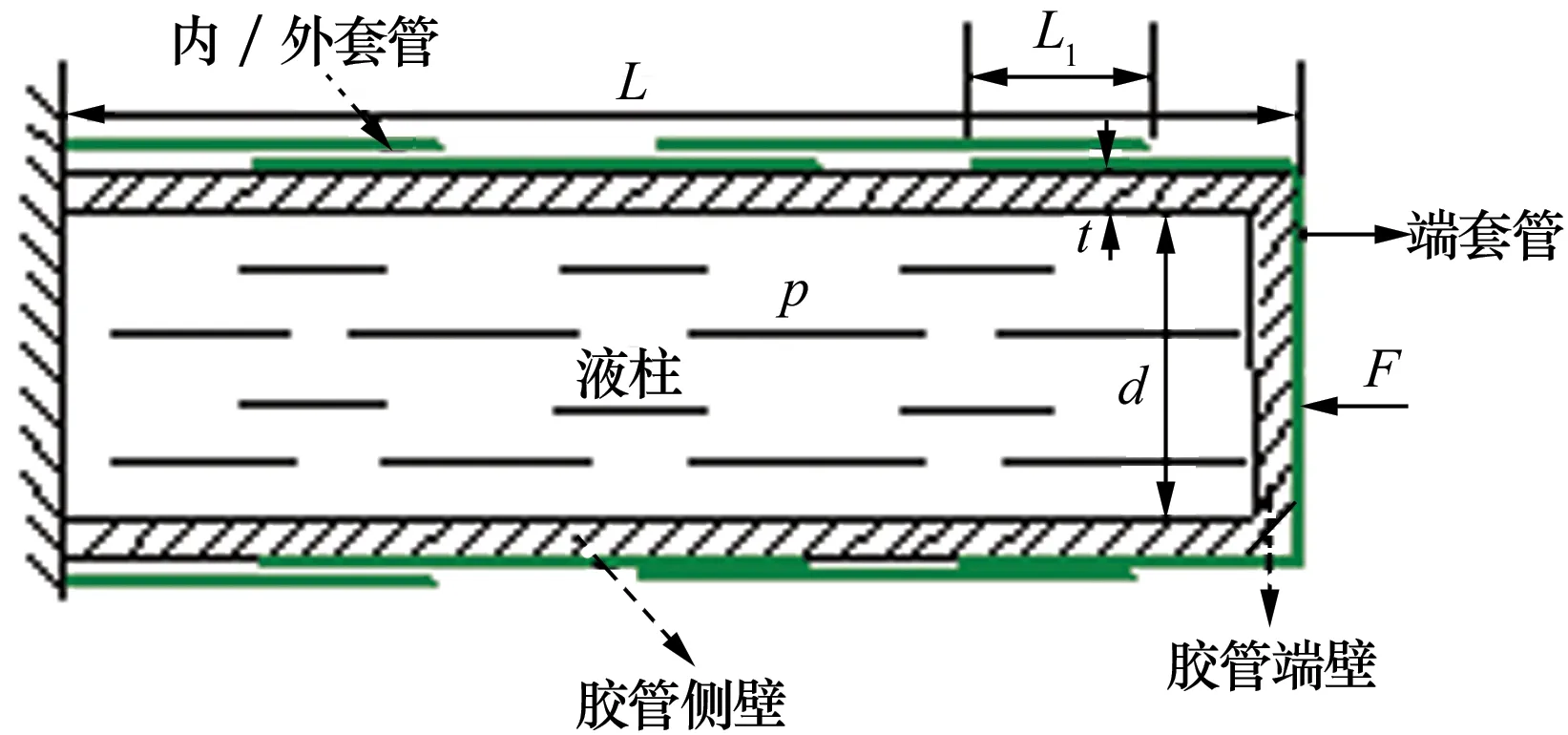
图2 可伸缩充压管模型及参数

充压管在工作状态下，管内压力为p，套管端部受到支反力F作用，结构处于平衡状态。此时胶管的长度增加至L，壁厚为t，内径为d。由于套管的径向约束，几何参数满足d+ 2t=d0+ 2t0。

2.2 等效刚度推导

在图3所示的平衡状态下，假设充压管端套沿轴向受到较小的压力增量ΔF，使得管长减小ΔL，油液压力增加Δp，如图3所示，则充压管的等效抗压刚度可以表示为Kc=ΔF/ΔL。通过取隔离体分析，对等效抗压刚度进行推导。

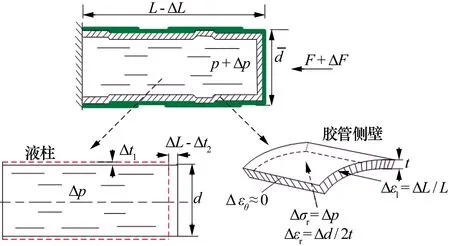
图3 可伸缩充压管等效抗压刚度分析

对于充压管，不考虑套管与胶管之间的摩擦，外力增量引起的平衡条件满足：

(1)

对于胶管内液柱，压力增加Δp，体积增加ΔV，与有效体积模量βe满足：

(2)

式中，V为封闭油液的体积，满足V≈Lπd2/4。

在Δp作用下，胶管壁产生变形，其中侧壁厚度减小Δt1，端壁厚度减小Δt2，则：

(3)

将式(3)代入式(2)得：

(4)

对于胶管的端壁，其厚度变化Δt2与压力增量Δp满足：

(5)

对于胶管的侧壁，取微元体，在Δp作用下，其应力增量满足平衡：

(6)

式中：轴向应变增量Δεl=ΔL/L；径向应变增量Δσr=Δp，Δεr=Δt1/t；胶管环向应变增量Δεθ≈0，代入式(6)得：

(7)

将式(5)和式(7)代入式(4)得：

(8)

将式(8)代入式(1)，再根据充压管等效抗压刚度的定义得到：

充压管在工作状态下油压一般在2～8 MPa范围内，在该压力下，橡胶压缩模量Ec与βe相比不能忽略，且二者都比Et大很多，因此等效抗压刚度可以简化为：

(9)

对于油液有效体积模量βe，文献[10]给出了某航空常用液压油在常温、2%含气量下，βe与油压p的试验拟合曲线，满足：

βe=f(p)=0.43p3-18.6p2+268.6p-10

代入式(9)可得Kc和p的关系曲线，如图4所示。

图4 充压管等效抗压刚度随油压变化关系

在不考虑胶管层时，即液压油直接与刚性器壁接触，充压管的等效抗压刚度主要由油液的βe决定；而考虑胶管壁的影响后，等效抗压刚度发生了明显的折减。

3 充压管在自适应机翼中的应用分析

3.1 某自适应机翼构型

图5给出了一种自适应机翼构型方案，由单块式机翼盒段和自适应后缘组成，利用后缘的光顺变形，可以调节翼型弯度。

在自适应后缘内部塞满轻质、可变形的填充物，将可伸缩充压管埋入填充物上下表面，两端与纵筋相连，沿着展向形成阵列结构，实现后缘的分布式驱动。

图5 某自适应机翼构型方案

充压管采用弹簧单元建模，弹性系数与压力有关，仿真分析时，在驱动后缘变形时，油路打开，此时充压管不能当作结构件，弹簧单元不被激活；当变形到目标位置后，油路关闭，此时充压管可以当作承压结构件，弹簧单元激活。计算出管内压力，由式(9)可得充压管的弹性系数。

3.2 自适应后缘振动变形分析

扰动载荷作用1.5 s后释放，结构阻尼取为0.03。图6为机翼后缘驱动到目标位置偏转15°时，在扰动载荷下后缘末端的振动变形，分别考虑了不加充压管和加入充压管2种情况。若不考虑充压管刚度，后缘末端将在平衡位置产生上下约4°偏转角变化；而引入充压管刚度后，后缘的抖动角度控制在0.6°以内，起到了良好的抗扰动变形作用。

4 结束语

本文设计了一种可伸缩充压管驱动器，具有重量轻、驱动力和驱动位移大等特点，可以实现对可变形结构的分布式驱动。

针对可伸缩充压管的“驱动件即结构件”特点，通过建模分析推导了充压管抗压刚度的工程简化公式。

将可伸缩充压管驱动器应用于自适应机翼后缘上，满足结构的驱动需求，并能有效提高后缘抵抗扰动载荷的能力。

[1] WEISSHAAR T A. Morphing aircraft systems: Historical perspectives and future challenges[J]. Journal of Aircraft, 2013, 50(2): 337-353.

[2] 徐文. 美国空军的传感器飞机计划[J]. 飞航导弹, 2005(3): 3-4.

[3] 杨智春, 解江. 自适应机翼技术的分类和实现途径[J]. 飞行力学, 2008, 26(5): 1-4.

[4] REICH G, SANDERS B. Introduction to morphing aircraft research[J]. Journal of Aircraft, 2007, 44(4): 1059.

[5] MERTMANN M, VERGANI G. Design and application of shape memory actuators[J]. The European Physical Journal Special Topics, 2008, 158(1): 221-230.

[6] MONNER H P. Realization of an optimized wing camber by using formvariable flap structures[J]. Aerospace Science and Technology, 2001, 5(7): 445-455.

[7] BHARTI S, FRECKER M I, LESIEUTRE G, et al. Tendon actuated cellular mechanisms for morphing aircraft wing[C]// Proceedings of SPIE Modeling, Signal Processing, and Control for Smart Structures, San Diego, CA, 2007.

[8] BARRETT R M, VOS R, TISO P, et al. Post-buckled precompressed(PBP) actuators: enhancing VTOL autonomous high speed MAVs[C]// Proceedings of 46th AIAA/ASME/ASCE/AHS/ASC Structure, Structural Dynamics & Materials Conference, Austin, TX, 2005.

[9] BARBARINO S, AMEDURI S, LECCE L. Wing shape control through an SMA-based device[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(3): 283-296.

[10] 从恒斌, 王贵桥, 郑宏伟. 液压油和软管的等效体积弹性模量测定[J]. 机床与液压, 2010, 38(5): 81-83.

张 平(1985-)，男，博士，工程师，主要研究方向为智能蒙皮设计、复合材料力学。

Study on a Pressurized Telescopic Tube Actuator and Its Application

ZHANG Ping1,2

(1.The38thResearchInstituteofCETC,Hefei230088,Chia； 2.NationalIndustrialDesignCenter,Hefei230088,China)

Adaptive technology is considered as one effective approach to enhance the endurance ability of sensor-craft, and the drivers are the basic system to keep adaptive structures working. In this paper, a kind of pressurized telescopic tube actuator which is capable of both driving and bearing is proposed. The mechanical model of the telescopic tube is established and then its simplified formula of equivalent stiffness is derived. Finally the telescopic tube actuator is applied to an adaptive wing and the vibration deformation of wing under airflow disturbance is simulated. Results show that the pressurized telescopic tube actuator is capable of producing enough driving force and displacement, also providing effective structure stiffness for adaptive structures.

sensor-craft; adaptive technology; pressurized telescopic tube

2016-10-10

V224

A

1008-5300(2016)06-0048-04