数学思想方法在初中数学合作学习模式中的应用

赵圣柱（山东省济南实验初级中学）

数学思想方法在初中数学合作学习模式中的应用

赵圣柱
（山东省济南实验初级中学）

在新课程改革的教育背景下，如何将数学思想方法应用在初中数学合作学习模式中是教师需要解决的问题。在初中数学合作模式中应用数学思想方法，有利于培养初中生的数学思维，培养初中生的抽象思维能力，培养初中生良好的数学学习习惯。

数学思想；初中数学；合作学习；教学模式；问题；策略

初中数学作为一门重要的科目，在教学中应引起教师与学生足够的重视，因为其抽象性与理性化特征较为显著，对于初中生的学习而言，存在一些困难和阻碍。随着21世纪科学技术的不断发展与完善，数学科学已在众多领域得到较为广泛的应用，传统的初中数学课堂教学模式已经不能适应当前的课堂发展，不能满足初中生对数学课堂学习的需要。

一、数形结合思想在初中数学合作学习模式中的应用

在数学解题中，数形结合是最常用的思想方法。数形结合思想可以将抽象的数学问题直观化、生动化，能将抽象思维转变为形象思维，便于学生把握数学问题的本质。在解题过程中运用数形结合，可以让学生快速地解决问题。在初中数学合作学习模式中应用数形结合思想，学生的学习有了方向性。当学生合作解决某道数学问题的时候，他们会共同使用数形结合思想，将抽象的数学问题形象化，便于学生在最快的时间将数学问题解决掉。

比如，当老师要讲解这样一道数学题的时候，即：汾河公园要建造圆形喷水池。在水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA=1.25m。由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m。试问：（1）如果不计其他因素，那么水池的半径至少要多少米，才能使喷出的水流不致落到池外？（2）如果水流喷出的抛物线形状与（1）相同，水池的半径为3.5米，要使水流不落到池外，此时水流的最大高度应达到多少米？在合作解决这道数学题的时候，学生要分析题中的量，根据题目中的量画出图形，然后再解决此道数学题。

二、分类讨论思想在初中数学合作学习模式中的应用

在我们遇到的数学问题中，有部分问题的结论并不是唯一确定的，有些问题的结论在解题过程中不能进行统一的论证，还有些题目中是用字母来表示已知量的，由于字母取值不同，因此，会影响到问题的解决。在解决此类问题的时候会划分成为不同的情况，然后再逐一解决。在合作学习模式的影响下，每位学生要发挥自身的主动性思考问题，不要局限自身的思维，而是要结合自身的学习经验来巧用分类讨论思想。

比如，当老师要讲解这样一道数学题的时候，即：三角形ABC的边AB为15厘米，边AC为13厘米，边BC上的高AD为12厘米，求此三角形的面积。该道题目中并没有指明三角形的形状，所以学生需要分类讨论。在分类讨论时，学生可以将三角形分为锐角三角形、钝角三角形，以此来得出最终的答案。在合作学习模式下，每位学生都有不同的想法，因此，在解决同一道数学题时，每位学生要表述自身的想法，将分类讨论思想运用到其中，提高自身解题的效率。

三、转化思想在初中数学合作学习模式中的应用

转化思想又被称为化归思想，其是将一个问题由难化易，由繁化简，由复杂化简单的过程。转化既是一种重要的解题思想，又是一种有效的数学思维方式。配方法、待定系数法、整体代入法等都用到了转化思想。转化思想的运用降低了学生解题的难度，提高学生解题的精准度。

比如，当老师要讲解这样一道数学题的时候，即：如下图是一块在电脑屏幕上出现的矩形色块图，由6个颜色不同的正方形组成，设中间最小一个正方形边长为1，则这个矩形色块图的面积是多少。在解此道数学题的时候，要运用转换思想，用代数考虑，将问题用一个方程表达出来，从而求出次小正方形的边长，最终求得面积。

四、方程思想在初中数学合作学习模式中的应用

方程思想是对于一个问题用方程解决的应用，也是对方程概念本质的认识，通过分析数学问题中变量间的等量关系，构建方程，或者利用方程的性质去分析、转换、解决问题。

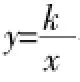
在解此道题的时候，学生可以通过联立方程组来解决，在联立方程后会得到一个一元二次方程，如果没有交点意味着这个方程误解。通过运用方程思想来解此题，整个题的难度降低了，学生之间通过合作快速找到了该问题的答案。

数学思想方法，从本质上讲是一种数学思维方式，是发现与解决数学问题的根本方法，是对数学知识的提炼与总结，是数学知识的精髓所在。在初中数学合作学习模式中应用数学思想方法，有利于培养初中生对于初中数学学习的兴趣，有利于培养初中生良好的数学学习习惯与思维方式。

［1］黄夏秋.数学思想方法在高中数学函数章节中的全面渗透［J］.考试周刊，2015（92）.

［2］陈书宝.论初中教学中数学思想方法的渗透［J］.理科考试研究，2015（24）.

·编辑王团兰