放缩法在高中数学中的应用

郑春灵（广东省惠州市东江高级中学）

放缩法在高中数学中的应用

郑春灵
（广东省惠州市东江高级中学）

高中数学是高中生在高中阶段学习的重点及难点课程，其解题方法多种多样，主要探讨高中数学解题方法中的放缩法。

放缩法；函数；不等式

高中数学的学习内容繁多，解题方法多样，学生难免会产生畏难、抵触情绪。因此，要想提高课堂的教学质量，提高学生的学习成绩，教师就要把知识点串联起来，让学生在脑中形成整体的框架。下面本文主要从函数、数列、不等式及解析几何这四个方面探讨一下放缩法的应用。

一、放缩法在函数中的应用

函数部分是高中数学教学中的难点与重点。在高考中函数部分的题占有很大的比重，由于函数的题型复杂多变，一个不同的条件，解题思路就会截然不同，因此很多学生学起来都觉得很困难。下面我就简单分析一下放缩法在函数证明题中的作用。

又因为n∈N*且n≥3，所以只需证：2n＞2n+1，

分析：此题涉及用二项式定理法的放缩，将二项式定理与函数结合起来运用放缩法解题也是近年来高考的重点。很多学生在看到这道题后，都能很快地想到利用作差的方法将该题进行简单的变形，将n代入函数关系式中，从而经过推导得出须证2n＞2n+ 1。然后很多学生就束手无策了，其实看到这样的式子，我们就要在脑海里搜索，什么样的表达式跟它相关，然后就能想到二项式，利用二项式定理法就能将该题简单地进行转化，从而放缩得出所求结论。

放缩法在函数中的应用较为普遍，因此，教师在高中数学课堂教学过程中，要注意学生对知识的综合掌握，以便于能够综合利用所学的知识，采用最简便快捷的解题方法，提高解题的效率，提高学习的质量。

二、放缩法在数列中的应用

放缩法在数列中的应用可以分成两种思路，即先求和后放缩、先放缩再求和两种。下面我举几个简单的例子来帮助学生了解一下解题思路。

（一）先求和再放缩

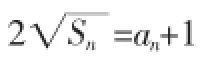
（1）数列｛an｝的通项公式；

解：（1）由已知得：4Sn=（an+1）2，当n≥2时，4Sn-1=（an-1+1）2，

将两式进行作差，得：4an=an2+2an-an-12-2an-1，

将上式进行整理，有（an+an-1）（an-an-1-2）=0，

又因为｛an｝为正数数列，

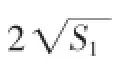
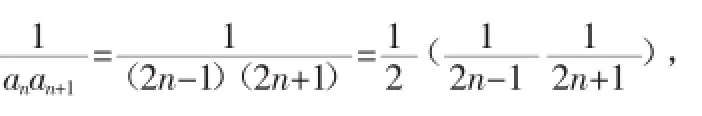
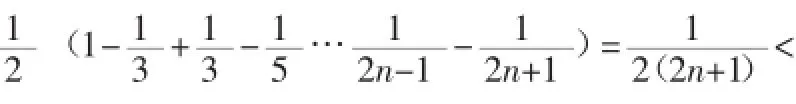
分析：由于该题的已知条件为数列通项与前n项和的关系，那么，学生自然而然地就想到利用作差的方式来求数列的通项公式。对于问题（2），根据学生的做题经验以及总结，由于an的通项公式的特征，那么我们很容易就想到要利用裂项相消的方法来求bn的通项公式，从而得出bn的前n项和，再利用函数的基本性质得出该题的证明结论。

总结：在做题时我们一般先分析数列的通项公式，如果此数列是等差或等比数列，就可以直接进行求和，或是能通过变形转化为等差、等比数列，再进行求和，再或者，可以利用裂项相加减求和、分组求和、倒序相加等求和方法求和。

（二）先放缩再求和

1.放缩成等差数列求和

例.已知各项均为正数的数列｛an｝的前n项和为Sn，且an2+an= 2Sn

解：（1）由条件可知，若令n=1，则可以得到a1+a12=2S1=2a1，

因为a1＞0，所以a1=1。

又由条件可知：an2+an=2Sn，则an+12+an+1=2Sn+1。

上述两式相减可得：an+12+an+1-an2-an=2Sn+1-2Sn。①

又∵an+1=Sn+1-Sn，代入①可得：an+12+an+1-an2-an=2an+1

整理后得：（an+1+an）（an+1-an-1）=0

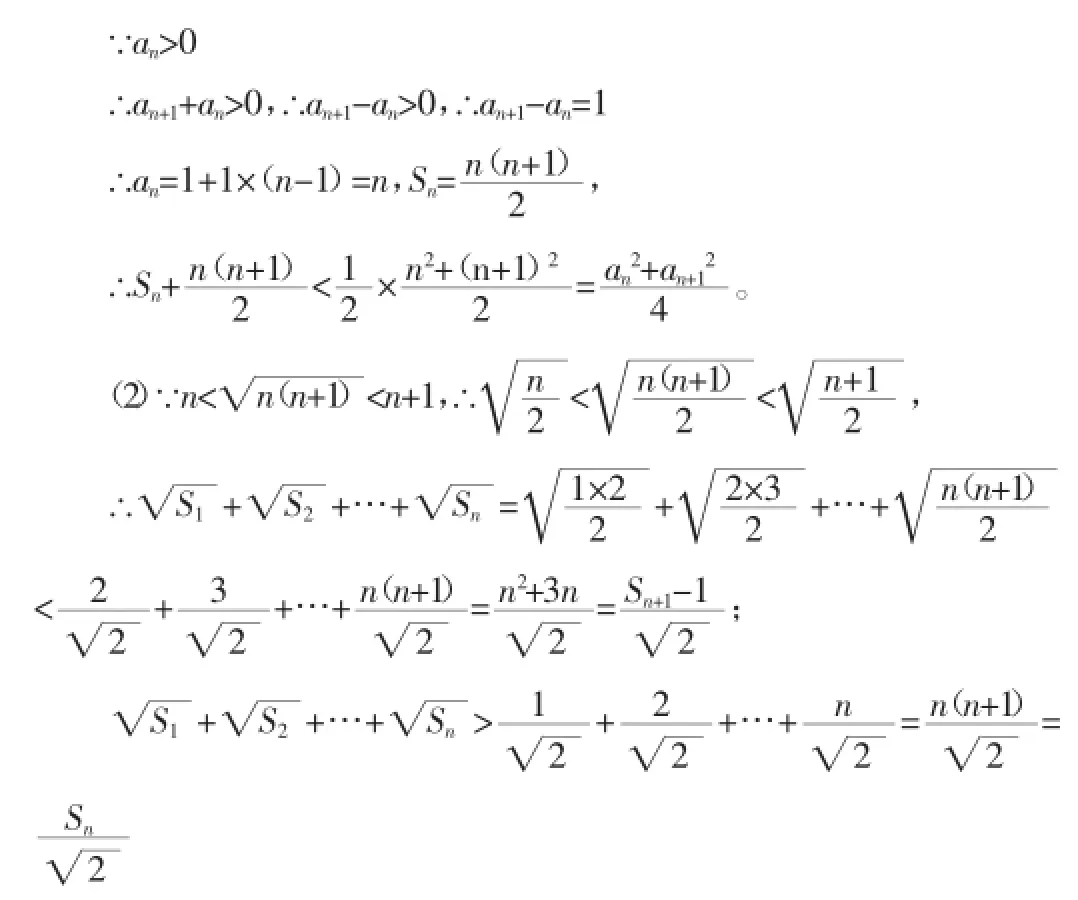
分析：由于给定的已知条件是数列通项an与前n项和Sn的关系，那么，学生自然而然地就想到利用作差的方式来求解，通过计算找出an+1与an的关系，得出数列｛an｝的公差为1，进一步再求证完成。对于（2）问，我们就要将已知与结论结合起来，并根据已经得证的结论运用合理的放缩，此题的放缩是问题的关键，若是放缩不恰当，得出的结论就难以证明该题，从而觉得该题无从下手，没有解题的技巧，只有熟练掌握放缩的原则，运用合适的方法，才能够得出正确结论。因此，我们在数学课堂教学中，也要让学生学会总结与反思，从而使他们的思维能够深化，在解题时能够多方面思考，从而快速地找到解题思路。

2.放缩成等比数列求和

例.（1）（2012年广东卷）设数列｛an｝的前n项和为Sn，满足2Sn=an+1-2n+1，n∈N*，且a1，a2+5，a3成等差数列。

①求a1的值；

②求数列｛an｝的通项公式；

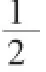
解：（1）①略；②an=3n-2n

③∵an=3n-2n=（3-2）（3n-1+3n-2×2+3n-3×2+3n-3×22+…+2n-1）≥3n-1

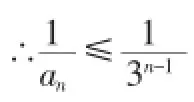
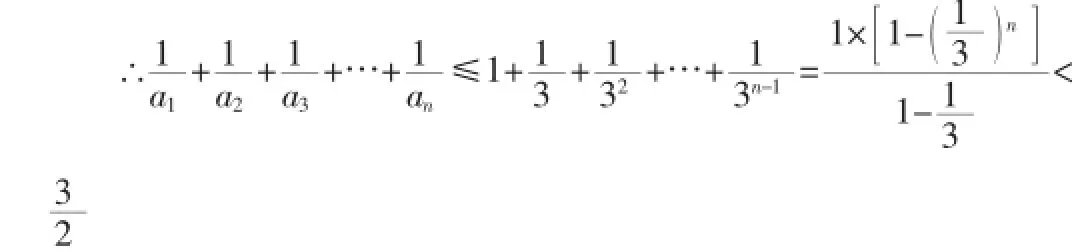
（2）∵A9-A7=a8+a9，A8-A9=-a9，a8+a9=-a9，

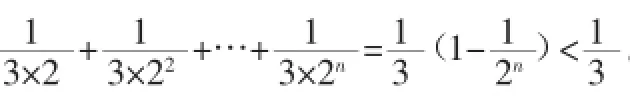
分析：该题的数列｛bn｝既不是等差数列，也不是等比数列，但是要对其进行求和，那么，我们只能将其进行放缩，根据其通项的特点以及要求的结论，找到合适的放缩方向，从而得出结论。这就要求学生对平时的学习过程加以重视，积累每道题的解题思路与方法，久而久之就能够快速地找到解题技巧。

3.放缩为差比数列求和

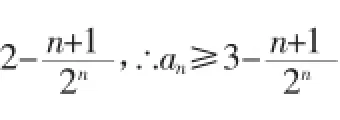
4.放缩为裂项相消求和

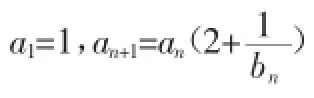
（1）求f（x）的最大值；

（2）求数列｛an｝｛bn｝的通项公式；

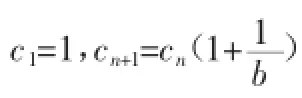
解析，（1）利用导数求最大值、此略。

（2）an=2n-1（叠乘法），bn=2n-1（待定系数法）。

由（1）ln（1+x）＜x（x≥0）

分析：放缩成差比数列与放缩成裂项相消这两种方式，主要要求学生对这类题有一定的积累，从而在做题时能够准确地找到解题思路，用这种仿佛解题可以有效地提高效率，节省做题时间。

以上例题通过不同的解题方法，比较全面地说明了放缩法在数列解题中的应用，不同的解题方法，其思路基本一致，即放缩与求和，只要将这两个部分灵活运用，那么，运用放缩法解数列题就不成问题，反而学生还会觉得这个解题过程充满趣味。

三、放缩法在不等式中的应用

放缩法在不等式证明中常在多项式中“舍掉一些正或负”从而使不等式各项之和产生变化，变大或变小。又“在分式中放大或缩小分式的分子分母”，或“在乘积式中用较大（较小）因式代替”等效法，而达到其证题目的。如重庆高考题：

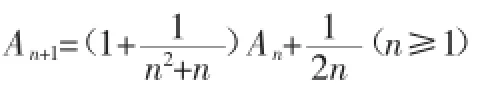
（Ⅰ）用数学归纳法证明An≥2；

（Ⅱ）已知不等式ln（1+x）＜x对x＞0成立。

证明：An＜e2（n≥1），其中无理数e=2.71828…

分析：由题目的已知条件，提示的思路很明确，首先要根据该题式子的特点，对等式两边取对数，即证明ln An＜2，而在已知An+1与An的递推关系的基础上，就应该考虑是否要去掉一些项来进行放缩。

证：（Ⅰ）略。（Ⅱ）由递推公式及（Ⅰ）结论有：

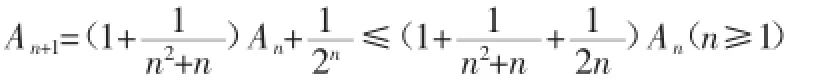
两边同时取对数，利用已知的不等式，可得：

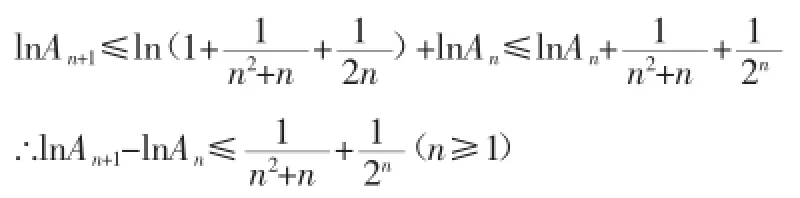
上式从1到n求和可得：

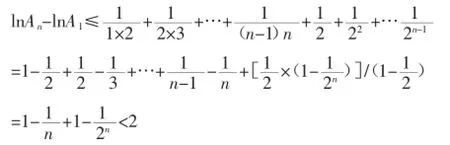
∴ln An＜2，故An＜e2（n≥1）

小结：本题解题过程中同时使用了多种放缩技巧，如舍项放缩与裂项放缩等，并在放缩的过程中构造等比数列，技巧性和知识综合度要求比较高。因此，教师在讲课时，要将各知识点串联起来进行讲解，让学生在脑中形成整体的框架，对数学知识形成整体的轮廓，以便学生在做题时，不会局限在一个知识点中，从而能够有效地发散学生的思维。

再比如全国卷这道高考题，利用不等式的基本性质来进行放缩：

（Ⅰ）求a3+b3的最小值；

（Ⅱ）是否存在a，b，使得2a+3b=6？并说明理由。

分析：该题只是利用了不等式的性质进行放缩，因此解题十分简单。只要学生的基础知识牢固，就能快速地解决此题。这就要求高中数学教师在讲解数学题时，要注重学生对基础知识的掌握情况，学生只有掌握了扎实的基础知识，才能够做到知识的融会贯通。

四、放缩法在解析几何中的应用

解析几何的教学内容也是高中数学学习的难点内容，其各种曲线的轨迹方程变化多端，是综合性很强的题型。下面我就简单举个例子来说明一下放缩法在解析几何中的应用。

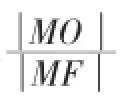
分析：该题将不等式的性质与解析几何的知识进行了融合，运用不等式法进行放缩，只有熟练掌握这两部分的知识，才能够快速解题。

综上所述，在数学的教学中，教师要时刻注意培养学生的解题技能，让学生反复练习这几种方法，并且引导他们举一反三。同时教师要注重学生对基础知识的掌握情况。只有学生在扎实的基础上，熟练掌握各个知识点，才能够将其联系起来，融会贯通，从而能够快速而准确地找到解题的思路，提高解题的效率。

［1］朱国宏.探析数列型不等式证明中“放缩法”的妙用［J］.高中数理化，2014（5）.

［2］张徐生.放缩有度，顺应目标：例谈放缩法在证明不等式中的应用［J］.数学教学研究，2007（9）.

·编辑段丽君