掌握解题技巧 突破解题障碍 培养创新思维

林公兴（福建省泉州第九中学）

掌握解题技巧突破解题障碍培养创新思维

林公兴
（福建省泉州第九中学）

《普通高中数学课程标准》指出，数学教育要面向全体学生，实现人人学有价值的数学，人人都能获得必须的数学，使不同的学生在数学上得到不同的发展。学生在解答一些简单高中数学题目时常常碰到障碍，往往是因为知识存在缺漏。扎实的知识功底、一定量的练习和解题技巧是突破解题障碍的必要条件。在选择、填空题的解题中，采用特值法可以有效降低难度，从而突破解题障碍；在解答题中，遵循一般解题原则是突破解题障碍的有效途径。在实践中，教师应发挥学生的主动性和创造性，把数学知识转化为激发学生的“药引”，培养创新思维，引发学生的进取心和求知欲，才能取得好的教学效果。

解题障碍；特值法；解题技巧；创新思维

在高中数学教学中常常会遇到这样的问题，学生在解答一些简单数学题目碰到障碍，往往是因为知识存在缺漏。这样，碰到障碍自然是在所难免。笔者从多年的高中数学教学中感受到，扎实的知识功底、一定量的练习和解题技巧是突破解题障碍的必要条件。

一、在选择、填空题的解题中，采用特值法可以有效降低难度，从而突破解题障碍

例:（2015全国理12）设函数f（x）=ex（2x-1）-ax+a，其中a＜1，若存在唯一的整数x0使得f（x0）＜0，则的取值范围是（）

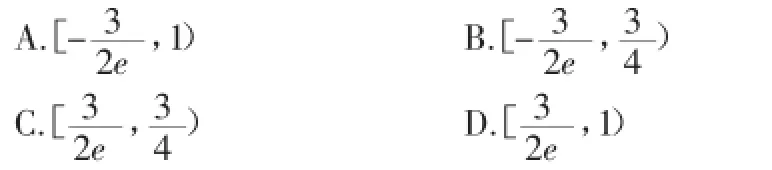
图1

图2

图3

解析：本题考查平面向量的加减数乘运算及平面向量的基本定理。向量的运算若能坐标化，则大大简化运算，降低难度。故对△ABC取特例，使得AC=3，BC=2，∠ACB=90°，如图3建立直角坐标系，则M（1，0），N（0，1），A（3，0），B（0，2），C（0，0）

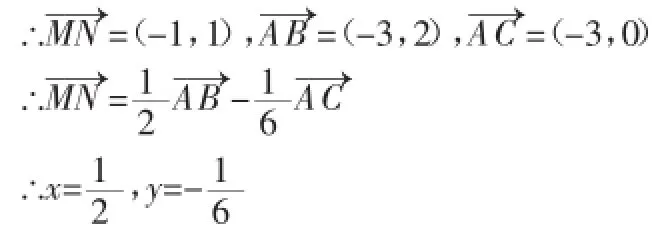
二、在解答题中，看到题目无从下手是学生常常出现的问题，遵循一般解题原则是突破解题障碍的有效途径

例：在△ABC中，若∠A，∠B为锐角，且sin2A+sin2B=sin C，试判断△ABC的形状并给予证明。

解析：看到上式容易联想到sin2A+sin2B=sin C（①）。若是①式，则通过角化边，容易证明△ABC为直角三角形，在sin2A+ sin2B=sin C中，右边缺失一个sin C的情况下，也不难判断△ABC为直角三角形。但证明是该题的难点，在判断三角形形状的问题上，对已知条件处理的一般原则是“边化角，角化边”，统一边、统一角。sin2A+sin2B=sin C中只有角的关系，有三个未知角，我们一般可以转换掉一个。根据协调性，我们往往会转换掉角C。

本研究选取微波消解法和电感耦合等离子体发射光谱法（ICP-OES）相结合的方式检测面制食品中的铝含量，并对样本进行了实验前有效处理，确保仪器保持正常运行，检测值确定为O．027μg/ml，偏差控制在1.59%以内，加标回收率的计算值处于92.4%－104.6%之间。最终证实此方法具有检出限低、操作方便简单、测定精度高等优点。所以，可以在面制食品铝含量的测定中运用这一方法。

解法一:

∵sin2A+sin2B=sin C

A+B+C=π

∴sin2A+sin2B=sin（A+B）

=sin A cos B+cos A sin B

∴sinA（sin A-cos B）+sin B（sin B-cos A）=0

∵sin A＞0，sin B＞0

∴（sin A-cos B）（sin B-cos A）≤0

以上三角函数的化简计算有一定的难度，又是一个解题障碍。当问题正面解决较困难时，不妨从反面考虑一下，若△ABC不是直角三角形，则sin C≠1，即0＜sin C＜1，则sin2A+sin2B＜1，此时式子就和谐了，更容易转化了。

解法二：假设△ABC不是直角三角形，则sin C≠1，即，0＜sin C＜1，则sin2A+sin2B＜1，

∴sin2A＜cos2B，

∵A，B为锐角，

∴△ABC为钝角三角形且cos C＜0。

又 sin2A+sin2B=sin C⇒a2+b2=2Rc=c2+2ab cos C⇒2Rc-c2= 2ab cos C

∴2Rc-c＜0即2R＜c，与事实矛盾，故假设不成立，△ABC为直角三角形得证。

数学教学应从“知识传授”的传统模式转变到“以学生为主体”的参与模式，注重数学思想方法的渗透和良好的思维品质的形成，注重学生创造精神和实践能力的培养，这是素质教育的要求，也是其根本所在。在实践中，教师应发挥学生的主动性和创造性，灵活使用教材，设计新的教学过程，把数学知识转化为激发学生的“药引”，引发学生的进取心和求知欲，才能取得好的教学效果。

·编辑段丽君