脉冲噪声中基于数据可信度加权的跳频信号检测
2016-09-07李曙光姬红兵
金 艳, 李曙光, 姬红兵
(西安电子科技大学电子工程学院, 陕西 西安 710071)
脉冲噪声中基于数据可信度加权的跳频信号检测
金艳, 李曙光, 姬红兵
(西安电子科技大学电子工程学院, 陕西 西安 710071)
时频分析是跳频(frequency-hopping,FH)信号检测的有力工具,但是脉冲噪声下性能严重退化,无法有效地提取跳频信号的周期、频率和跳变时刻等参数;基于分数低阶统计量和最大似然估计(maximum-likelihood,ML)的算法是改善脉冲噪声下FH信号时频分布的两类常用方法,但前者性能改善有限,后者通常对噪声的概率分布较为敏感,且计算复杂度高。对此,提出一种基于数据可信度加权(weightingbasedonthedatacredibility,WDC)的FH信号检测方法。该方法基于云模型(cloudmodel,CM)理论,建立了数据可信度的概念,以分析脉冲噪声下接收信号的不确定性,然后在此基础上实现信号加权,改善脉冲噪声下FH信号的时频分布特征。仿真实验证明,在稳定分布噪声中,该方法与基于分数低阶及Myriad滤波器的时频分析方法相比,能够较好地抑制脉冲噪声,获得FH信号的参数信息,具有良好的鲁棒特性。
数据可信度; 云模型; 跳频信号检测; 时频分析; 脉冲噪声
0 引 言
作为一种重要的扩频通信技术,跳频(frequencyhopping,FH)信号以其优良的组网能力、抗干扰能力和保密性在军事与民用通信中得到广泛应用。在日益复杂的电磁环境下,有效地截获FH信号,识别FH电台的频率集变得日益困难,因此,FH信号检测成为近年来扩频通信研究的热点。在传统信号处理中,一般用高斯分布描述背景噪声。但是,实际的噪声或杂波,如低频大气噪声、多用户干扰、海杂波等具有显著的脉冲特性。在该类噪声环境中,传统以高斯分布为噪声模型的FH信号检测方法不再适用[1]。
针对FH信号的检测问题,国内外学者做了大量的研究。传统的参数法主要基于最大似然(maximum-likelihood,ML)估计理论,如Myriad滤波器方法[2]和稳健理论下的时频分析方法[3]。但基于ML估计的方法受噪声的概率分布影响大,通常需要对非线性代价函数优化,计算复杂度高。传统的非参数检测法,主要有短时傅里叶变换(short-timeFouriertransform,STFT)[4]、维格纳-威利分布(Wigner-Villedistribution,WVD)[5]等。脉冲噪声环境下,通常采用分数低阶(fractionallowerorder,FLO)[6]统计量或特殊的窗函数处理,如基于熵测度的STFT[7],可有效实现脉冲噪声的抑制。但FLO的方法在选取FLO阶矩时缺乏理论支撑,基于熵测度的STFT计算复杂且性能提高有限。
具有不确定性[8]的现象与事物,广泛存在于自然界中,噪声便是一种不确定性的体现。脉冲噪声环境中,噪声对接收信号造成的不确定性影响主要体现在:①随机性,体现在噪声造成的接收信号幅值的不确定性;②模糊性,体现在接收信号极值的噪声隶属度[9]。文献[8]提出了云模型(cloudmodel,CM)理论,在统一模糊理论和随机理论的基础上,建立了一个不确定性的量化统计模型。随后,证明了正态云模型(normalcloudmodel,NCM)的普适性。在数据分析中,该理论能够兼顾模糊性和随机性,已广泛应用于图像处理[10]、智能控制[11]和数据挖掘[12-13]等领域。
根据NCM理论,本文首先提出数据可信度的概念,然后分析脉冲噪声对接收信号造成的不确定性,并转化为定量的可信度,再基于可信度曲线对信号加权以抑制脉冲噪声,改善信号的时频分布。该方法可有效实现脉冲噪声下FH信号的检测。
1 α稳定分布噪声
稳定分布[14]具有厚重的拖尾和显著的脉冲特性,与高斯分布相比,能够更好地描述雷达、地震、声纳、生物工程等领域中的杂波干扰或背景噪声。稳定分布没有统一的数学表达式,但它的特征函数具备统一的数学表达式:
(1)
式中

(2)

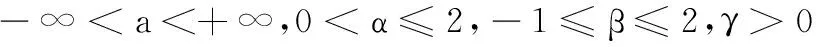
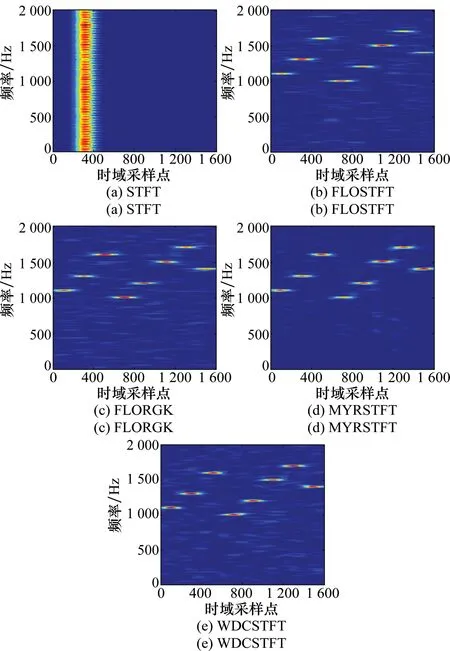
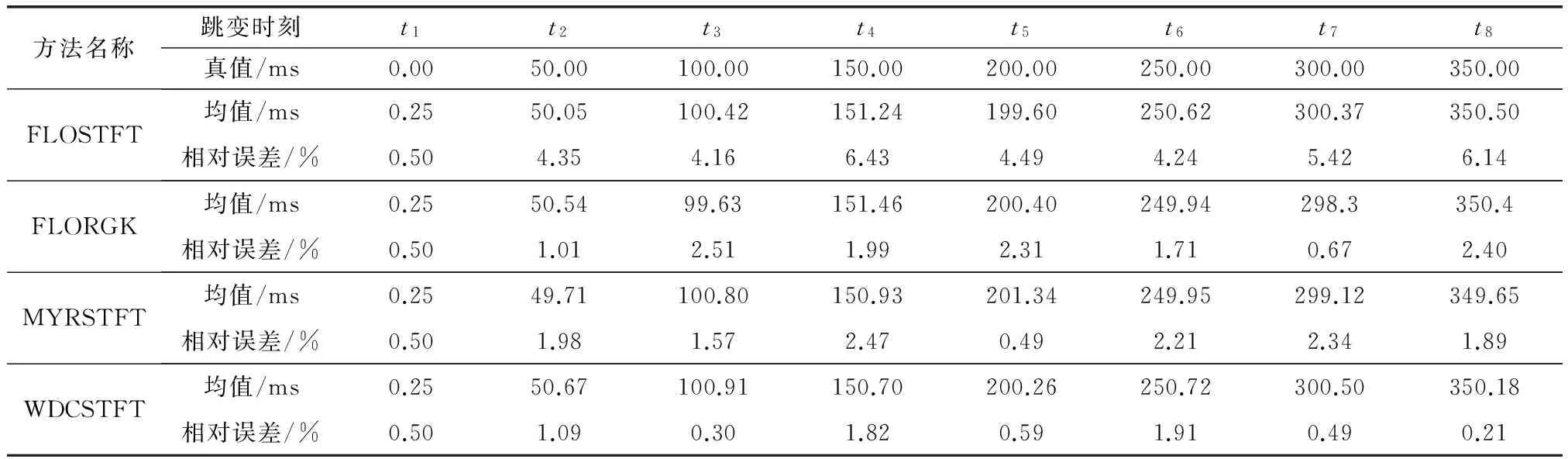
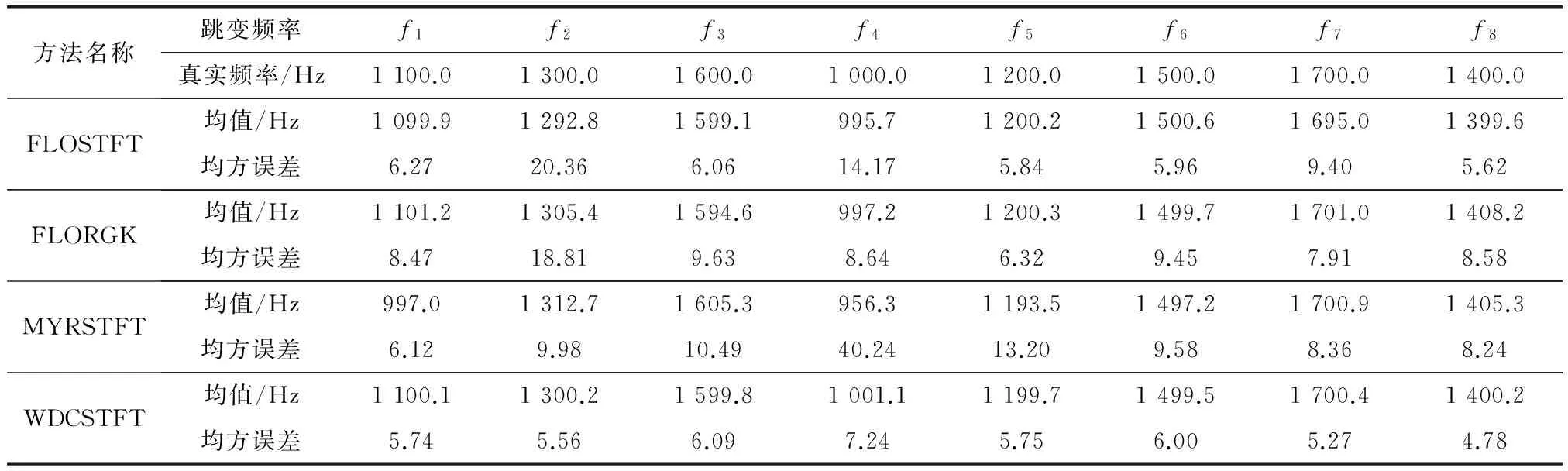
可知,α稳定分布的特征函数可由4个参数确定:α、β、γ、a。α为特征指数,α越小,分布越尖锐,拖尾越厚;β为歪斜系数,确定分布的歪斜程度,当β=0时对应于对称稳定分布,记为SαS。γ为分散系数,又称作尺度系数。a为位置参数,对于SαS分布,在0 由于α稳定分布没有二阶及以上矩,不存在方差,因此采用广义信噪比(generalsignal-noiseratio,GSNR)[19],表示为 (3) 脉冲噪声环境中,接收信号的不确定性主要表现在噪声造成的局部脉冲性,本文提出了可信度的概念来描述脉冲噪声对信号的影响。可信度定义为脉冲噪声条件下信号的可恢复程度,受脉冲影响越大,数据的可信度越低。通常情况下,信号在一定幅值范围内波动,是相对确定的,脉冲噪声造成信号局部短时间内的幅值急剧上升,形成尖峰,数据可信度降低。本文根据云模型理论,分析脉冲噪声下信号的不确定性,将这种不确定性定量表示为数据的可信度。 En′~N(En,He) (4) 数据与其不确定度形成的云状分布图称为云图,云图可直观表征样本对象中的不确定性信息。图1为云图示例,点状部分对应于Ex=0,En=1和He=0.1时的云图。实线部分为Ex=1,En=1和He=0时所得的云图。此外,实线云图也是点状云图的期望曲线。 图1 样本云图示例Fig.1 The example of a cloud distributed figure 根据NCM理论,可以对接收信号的数据做如下分析。 接收信号X的数据可信度为 (5) 其中,En′满足概率密度函数 (6) 将式(6)代入式(5)得 (7) 式(7)表明,对于任意的x,可通过数值积分计算得到相应的可信度。 (8) (9) 因为 (10) (11) Yi的概率密度为 (12) 即Yi的概率密度函数为 (13) 那么由X和Y构成的二维随机变量(x,y)的联合概率密度公式为 (14) (15) 依据该曲线,可对信号加权实现脉冲噪声的抑制 (16) 在时长为T的观测时间段内,接收到的FH信号[6]可表示为 (17) 式中,0 假设对接收信号采样后得到样本数为N的序列x{n}(n=0,1,…,N-1),采样频率为fs,首先采用基于数据可信度加权对信号消噪,然后通过时频分析,如STFT,进一步提取FH信号的参数信息。步骤如下: 步骤 1将加权处理后的信号进行STFT的时频分析,记为WDCSTFTs(k,l)。 步骤 2获得每一时刻k沿频率轴的最大值点,形成曲线,即 (18) pi=qi+Nh/2 (19) 步骤 5由以上跳变时刻可将处理后FH信号s(i)分成P段,记为sk(i)(i=1,2,…,P)。分别对每段进行DFT,检测各段FH频率,即 (20) 假设FH信号的参数为:跳频频率fk=[1.11.31.6 1.01.21.51.71.4]kHz,跳频周期T=50ms,采样频率fs=4kHz,观测时间为8个跳频周期,信号采样点数N=1 600,图2为该FH信号的时域波形。背景噪声则服从对称α稳定(SαS)分布[17],在广义信噪比(generalizedsignal-to-noiseratio,GSNR)GSNR=3dB的条件下,特征指数α=1.5和α=0.8时,FH信号的时域波形分别如图3(a)和图3(b)所示。 图2 FH信号Fig.2 The FH signals 图4给出了在GSNR=3dB时样本建立的数据可信度曲线。图4(a)和图4(b)分别为α=1.5和α=0.8时的可信度曲线,从图4中可以看出,样本经分析,处在可信度为0.1以下的数据量较少,一方面表明了脉冲噪声脉冲性越强烈其可信度的量化权值越小,另一方面也表明了脉冲噪声的稀疏性,和实际的脉冲噪声特点是相符的。比较图4(a)和图4(b),两者最显著的不同是图4(a)比图4(b)的权值横坐标跨度小,例如,当可信度为0.1时,α=1.5的横坐标区间为[-4.56,4.67],α=0.8的横坐标区间为[-9.68,10.14],这意味着前者的数据集聚性比后者好,噪声脉冲性越强,可信度的量度跨度越大。 图3 不同α值脉冲噪声中的FH信号Fig.3 The FH signals in α-stable noise with different α values 图4 可信度权值曲线Fig.4 The data credibility based weighting function 图5为脉冲噪声下,FH信号的时频分布图。在α=1.5,GSNR=3dB时,直接采用STFT所得的结果如图5(a)所示,可以看出,脉冲噪声造成了信号时间与频率分辨率的下降。基于FLO统计量的时频分布图如图5(b)和图5(c)所示,其中图5(b)为分数低阶的短时傅里叶变换(fractionallowerordershort-timeFouriertransform,FLOSTFT),图5(c)为分数低阶的径向高斯核函数(fractionallowerorderradiallyGaussiankernel,FLORGK)的时频分析。在阶矩p值的选取方面,目前缺乏相应的理论支撑。通过数值仿真分析,在p=0.2时,基于FLO统计量的时频方法分析性能接近或达到最优。因此,本文基于FLO的方法均采用该参数,由图5(b)、图5(c)与图5(a)相比可知,该方法可以较好地抑制脉冲噪声,改善FH信号的时频分布。图5(d)采用基于Myriad滤波器的方法(short-timeFouriertransformbasedonMyriad,MYRSTFT),该方法是基于柯西分布[2]进行的,需要对非线性代价函数进行优化,计算复杂度高,且可能收敛到局部极值点。图5(d)与图5(a)比较可知,Myriad滤波器的方法也可以较好地抑制脉冲噪声,且时频分布的聚集性得到进一步提高。采用本文方法(short-timeFouriertransformbasedondatacredibilityweighting,WDCSTFT)所得的结果如图5(e)所示,可以看出WDCSTFT对脉冲噪声具有很好的抑制效果,时频分布的聚集性得到明显提高。综上所述,在α=1.5,GSNR=3dB噪声水平下,WDCSTFT能够有效地获得FH信号的FH图案,较基于FLO统计量的时频分析方法和Myriad滤波器的方法,时间与频率分辨率得到进一步提高。 图5 FH信号的时频图Fig.5 Different time-frequency distribution of the FH signals 在FH周期检测方面,本文进行了200次蒙特卡罗实验,得出FH的周期均方误差,将其作为性能比较指标。图6为α=1.5和α=0.8时的FH周期均方误差性能曲线。从图6(a)可以看出,在α=1.5的条件下,当GSNR>3dB时,采用WDCSTFT可准确得到信号的跳频周期,在GSNR<-1dB时,检测性能开始退化;GSNR>1dB时,采用MYRSTFT的方法,可准确实现FH信号的周期检测;GSNR>0dB时,采用FLORGK的方法,可准确实现FH信号的周期检测;GSNR>3dB时,FLOSTFT才可准确检测出FH信号的周期。由此可知,在α=1.5时,采用WDCSTFT较其他方法在信号FH周期检测方面具备一定优势。从图6(b)可以看出,在α=0.8的条件下,当GSNR>3dB时,采用本文的方法(WDCSTFT)可准确得到信号的FH周期,当GSNR<3dB时,检测性能开始退化;GSNR>5dB时,采用MYRSTFT的方法,可准确实现FH信号的周期检测;GSNR>9dB时,采用FLORGK的方法,可准确实现FH信号的周期检测;GSNR>9dB时,FLOSTFT才可准确检测出FH信号的周期。由此可知,在α=0.8时WDCSTFT的方法较其他方法在信号FH周期的提取方面具有十分明显的优势。 图6 FH周期检测均方误差曲线Fig.6 The mean square error curves in FH cycle detection 表1 经过200次蒙特卡罗实验的跳变时刻误差统计(α=1.5,GSNR=3 dB) 表2 经过200次蒙特卡罗实验的跳变时刻误差统计(α=0.8,GSNR=5 dB) 在跳变频率检测方面,本文在GSNR=3 dB和α=1.5时,进行200次蒙特卡罗实验,所得的统计结果如表3所示。由表3可知,在该噪声水平下,WDCSTFT对跳变频率的检测标准差最大不超过4.38,而采用FLOSTFT、FLORGK和MYSTFT对跳变频率检测的标准差最大值依次为7.08、6.43、6.31。本文在GSNR=5 dB和α=0.8时,进行200次蒙特卡罗实验,所得的统计结果如表4所示。由表4可知,在该噪声水平下,WDCSTFT对跳变频率的检测标准差最大不超过7.24,而采用FLOSTFT、FLORGK和MYSTFT对跳变频率检测的标准差最大值依次为20.36、18.81、40.24。综上所述, WDCSTFT在跳变频率检测方面较其他方法准确度高,在强脉冲噪声中具有显著稳健性优势。 表3 经过200次蒙特卡罗实验的跳变频率误差统计(α=1.5,GSNR=3 dB) 表4 经过200次蒙特卡罗实验的跳变频率误差统计(α=0.8,GSNR=5 dB) 针对在脉冲噪声环境中,传统的FH信号检测方法不再适用的问题,本文依据NCM理论,从脉冲噪声对接收信号造成的不确定性的角度,提出了基于数据可信度加权的FH信号检测方法,同时较为详细地给出了相应的理论基础与算法过程。仿真实验证明,该方法能够有效地抑制脉冲噪声,实现对FH信号的检测。与常规的时频分析方法及基于ML估计的滤波方法相比,该方法提高了时频分辨率,在提取FH信号周期、跳变时刻和跳变频率方面,精度更高,具有良好的稳健性。 [2] Chavali V G, Da Silva C R C M. Detection of digital amplitude-phase modulated signals in symmetric alpha-stable noise[J].IEEETrans.onCommunications, 2012, 60(11): 3365-3375. [3] Katkovnik V, Djurovic I, Stankovic L. Robust time-frequency distributions[C]∥Proc.oftheIEEEInternationalSymposiumonSignalProcessingandItsApplications, 2001: 156-157. [4] Liu F, Ye F. Research on estimation SPWVD parameter of frequency-hopping signal[J].ComputerandInformationTechnology, 2007, 15(6): 28-30. (刘放, 叶菲. 跳频信号SPWVD参数估计方法研究[J].电脑与信息技术, 2007, 15(6): 28-30.) [5] Baraniuk R G, Jones D L. A signal-dependent time-frequency representation: optimal kernel design[J].IEEETrans.onSignalProcessing, 1993, 41(4): 1589-1602. [6] Jin Y, Liu J. Parameter estimation of frequency hopping signals in alpha stable noise environment[C]∥Proc.ofthe11thIEEEInternationalConferenceonSignalProcessing, 2012: 250-253. [7] Guo J T, Wang H Y. A new time-frequency representation based on ambiguity function analysis and its application in parameter estimation of FH signals[C]∥Proc.ofthe4thInternationalConferenceonWirelessCommunication,NetworkingandMobileComputing, 2008: l-4. [8] Li D Y, Liu C Y. Study on the universality of the normal cloud model[J].EngineeringScience, 2004, 6(8): 28-34. (李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学, 2004, 6(8): 28-34.) [9] Li D Y, Liu C Y, Gan W Y. A new cognitive model: cloud model[J].InternationalJournalofIntelligentSystems, 2009,24(3): 357-375. [10] Zhou Z. Cognition and removal of impulse noise with uncertainty[J].IEEETrans.onImageProcessing, 2012, 21(7): 3157-3167. [11] Li D Y. The cloud control method and balancing patterns of triple link inverted pendulum systems[J].EngineeringScience, 1999, 1(2):41-46.(李德毅. 三级倒立摆的云控制方法及动平衡模式[J].中国工程科学, 1999, 1(2): 41-46.) [12] Wang C Q. Study of rules extraction method based on two-dimension cloud model[J].ComputerEngineeringandApplications, 2010, 46(26):46-48. (王成全.基于二维云模型的规则提取算法研究[J].计算机应用与工程, 2010, 46(26): 46-48.) [13] Chen H, Li B. Qualitative rules mining and reasoning based on cloud model[C]∥Proc.ofthe2ndInternattonalConferenceonSoftwareEngineeringandDataMining, 2010: 523-52. [14] Liu M Q, Li B B, Cao C F. Recognition method of digital mo-dulation signals in non-Gaussian noise[J].JounalofElectronics&InformationTechnology, 2013, 35(1): 85-91. (刘明骞, 李兵兵, 曹超凤. 非高斯噪声下数字调制信号识别方法[J].电子与信息学报, 2013, 35(1): 85-91.) [15] Nikias C L, Shao M.Signalprocessingwithalpha-stabledistributionandapplication[M]. New York: Wiley,1995. [16] Pelekanakis K, Chitre M. Adaptive sparse channel estimation under symmetric alpha-stable noise[J].IEEETrans.onWirelessCommunications, 2014, 13(6): 3183-3195. [17] Zhong X, Premkumar A B, Madhukumar A S. Particle filtering for acoustic source tracking in impulsive noise with alpha-stable process[J].IEEESensorsJournal, 2013, 13(2): 589-600. [18] Aalo V A, Peppas K P, Efthymoglou G, et al. Evaluation of average bit error rate for wireless networks with alpha-stable interference[J].ElectronicsLetters, 2014, 50(1): 47-49. [19] Guo Y. The study on novel time delay estimation methods based on stable distribution[D]. Dalian: Dalian University of Technology, 2009. (郭莹. 稳定分布环境下的时延估计新方法研究[D]. 大连: 大连理工大学, 2009.) DetectionofFHsignalsbasedondatacredibilityweightinginimpulsenoiseenvironment JINYan,LIShu-guang,JIHong-bing (School of Electronic Engineering, Xidian University, Xi’an 710071, China) Time-frequencyanalysisisapowerfultoolforfrequency-hopping(FH)signaldetection,however,theperformanceoftime-frequencyanalysiswilldegradedrasticallyinimpulsenoiseenvironment,failingtoextractthehoppingduration,frequencyandtimingeffectively.Moreover,methodsbasedonfractionallowerorderstatisticsandmaximum-likelihood(ML)aregenerallyusedtoimprovetheperformanceofFHsignaltime-frequencydistribution,buttheperformanceimprovementoftheformerislimited,andthelatterisusuallysensitivetothenoisedistributionandhashighcomputationalcomplexity.TodetectFHsignalsinthepresenceofimpulsenoise,adetectionmethodofFHsignalisproposedbasedondatacredibilityweighting.Intheproposedmethod,theconceptofdatacredibilityisestablishedbasedonthecloudmodeltheorytoanalyzetheuncertaintyofthereceivedsignal.Onthisbasis,theweightingprocessisimplementedtothereceivedsignalandimprovestheperformanceoftime-frequencydistributionofFHsignalintheimpulsenoiseenvironment.SimulationresultsshowthatcomparedwiththefractionallowerorderstatisticsaswellastheMyriadfilterbasedtime-frequencyanalysismethods,theproposedmethodcandetecttheFHparameterswiththenoisebeingsuppressedeffectively,anditisrobustinthestablenoiseenvironment. datacredibility;cloudmodel;frequency-hopping(FH)signaldetection;time-frequencyanalysis;impulsenoise 2015-06-29; 2016-04-16;网络优先出版日期:2016-07-05。 国家自然科学基金(61201286);中央高校基本科研业务费专项资金(K5051202013);陕西省自然科学基金(2014JM8304)资助课题 TN911.7 ADOI:10.3969/j.issn.1001-506X.2016.09.29 金艳(1978-),女,副教授,博士,主要研究方向为现代信号处理、统计信号处理、非高斯噪声处理、信号检测与估计、通信信号侦测。 E-mail:yjin@mail.xidian.edu.cn 李曙光(1990-),男,硕士研究生,主要研究方向为非高斯噪声下跳频信号处理。 E-mail:lsg0419 @163.com 姬红兵(1963-),男,教授,博士研究生导师,主要研究方向为光电信息处理、微弱信号检测与识别、医学影像处理。 E-mail:hbji@xidian.edu.cn 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160705.1722.002.html
2 数据的可信度算法模型



3 可信度加权方法原理

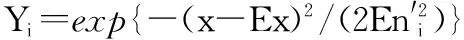

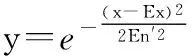

4 FH信号的参数提取
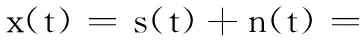

5 仿真实验及分析






6 结 论
