基于降维CKF和平滑的SINS/OD动基座对准

2016-09-07黄湘远汤霞清

系统工程与电子技术 2016年9期

关键词：对准基座降维

黄湘远, 汤霞清, 武　萌

(装甲兵工程学院控制工程系, 北京 100072)

基于降维CKF和平滑的SINS/OD动基座对准

黄湘远, 汤霞清, 武萌

(装甲兵工程学院控制工程系, 北京 100072)

为了提高捷联惯导(strapdowninertialnavigationsystem,SINS)/里程计(odometer,OD)动基座对准精度,使对准过程中具备一定精度的位置导航能力,提出了一种动基座非线性对准方法。首先对非线性系统进行简化并应用降维容积卡尔曼滤波(reduceddimensioncubatureKalmanfilter,RD-CKF)进行非线性对准,保证非线性对准过程中能够进行位置导航,对准结束时保证失准角为小角度。然后非线性R-T-S平滑至初始时刻进行校正,利用卡尔曼滤波再次对准,获得对准结束时刻高精度的姿态和位置导航。进行了实车实验,实验结果表明了方案的有效性。

容积卡尔曼滤波; 降维; 初始对准;R-T-S平滑

0　引　言

捷联惯性导航(strapdowninertialnavigationsystem,SINS)/里程计(odometer,OD)的组合导航已经成为陆用导航主要方式之一[1-2]。

晃动基座或动基座下SINS的初始对准常用惯性系对准方案[3-4],动基座对准中必须引入外参考速度和位置。由于里程计不能提供绝对的速度和位置信息,文献[5]提出一种动基座惯性系对准方案,忽略对准过程中的位置变化,长时间后位置误差较大。为了保证对准结束后位置精度,文献[6]设计了逆向导航算法,回溯到原点后进行再次导航,文献[7]基于同样的思路设计了SINS/多普勒测速仪(Dopplervelocitylog，DVL)组合导航的动基座对准方案。为了加快对准速度,文献[8]提出了基于状态估计的卡尔曼滤波逆向导航算法,文献[9-10]提出了严格逆向过程的罗经回溯对准和循环解算方法,为了充分激发误差,一次解算时间段不能太短。相关文献表明逆向思路的导航处理或状态估计可加快对准速度和解决对准结束后位置导航问题,都没有考虑对准过程中的位置导航。为了使对准过程中具有一定精度的位置导航能力,可使用SINS/OD非线性对准方案。

容积卡尔曼滤波(cubatureKalmanfilter,CKF)是一种优秀的非线性滤波器,精度高，数值稳定性强[11-12]。为了减小非线性对准中CKF的计算量,文献[13]设计了静基座下大方位失准角的降维CKF对准方案。本文基于SINS/OD非线性对准模型,首先对系统状态进行降维,推导了适合该模型的降维CKF算法。对准结束后方位精度较高,位置精度一般。为了提高对准结束后的位置精度,引入逆向处理。逆向处理过程也可通过非线性R-T-S平滑进行状态估计[14-15]来实现。

本文首先进行非线性对准,对准结束时利用R-T-S平滑和初始姿态进行修正,然后利用存储数据再次进行线性对准。最后进行了实车实验,结果表明，再次对准之后,方位精度得到一定提高,位置精度得到了较大的改善,该方案同时实现了高精度对准和位置导航。

1　SINS/OD非线性模型及简化

1.1SINS误差模型

首先定义相关坐标系,记惯性系为i系,地球系为e系,导航系n系为东北天坐标系，计算平台系为p系，载体系b系为右前上坐标系。

文献[16]给出了基于欧拉角误差模型的SINS姿态、速度和位置误差模型,本文将其改写成

(1)

式中,A′、A″、B′、B″、C′和C″均为3×3阶矩阵,非零项为

该模型要求纬度误差δL为小量,为了保证大失准角下δL为小量,通过位置、速度间歇性闭环反馈来修正SINS速度位置误差。

1.2OD误差模型

设OD坐标系为m系,y轴沿车体纵轴向前,x轴沿车体横轴向右,z轴构成右手系。

假设OD在ti-1～ti时刻内输出的脉冲数为Ni,则OD测得速度大小vD为

vD=KDNi/TD

(2)

式中,KD为OD标度因数;TD=ti-ti-1。

(3)

(4)

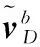
(5)

其中

1.3SINS/OD对准系统模型

(6)

(7)

系统噪声量w为

(8)

(9)

由式(1)、式(6)和式(9)构成SINS/OD初始对准的非线性系统,方程为

(10)

式中,f(x)和h(x)为非线性函数;系统噪声w～N(0,Q),测量噪声v～N(0,R), Q、R为噪声方差阵。

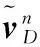
(11)

非线性系统退化为线性系统,可利用卡尔曼滤波完成对准。

1.4系统降维及状态分离框架

其次,SINS/OD动基座对准中,系统导航误差主要由大失准角φ导致,ξD引起的导航误差相对较小。因此,为了减小非线性滤波的计算量,可先不考虑ξD,将SINS/OD非线性对准系统进行降维。此时,系统状态量变为

(12)

系统观测方程变成

(13)

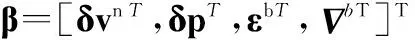
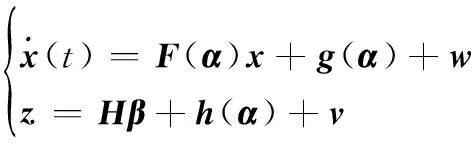
(14)

式中,F(α)为状态转移矩阵;g(α)、h(α)为非线性函数;H为线性矩阵。

2　基于降维CKF的非线性对准

考虑如式(15)所示的特殊非线性系统:

(15)

式中,αk为n维变量xk的前m个元素;βk为xk的后l=n-m个元素;系统噪声wk和观测噪声vk独立,wk～N(0,Qk)和vk～N(0,Rk)。

为了降低非线性滤波的计算量,基于“只采样非线性部分”的思路,引入降维CKF。针对系统式(15),设计对应的降维采样和滤波方式。

2.1时间更新

(16)

式中,Pξ为Px的前m行、m列子矩阵;Sx为Px的Cholesky分解阵；Sξ为Sx的前m行、m列子矩阵。且

步骤 1采样

步骤 2状态传播

计算Fi=F(ξi,k-1),gi=g(ξi,k-1),Θi=Θ(ξi,k-1),Φi=Φ(ξi,k-1),Ψi=Ψ(ξi,k-1),Ωi=Ω(ξi,k-1)。

(17)

2.2量测更新

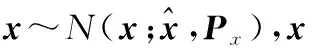
(18)

式中,Pξ为Px前m行、m列子矩阵,Pη为Px后l行、l列子矩阵,Pξη为Px的前m行、后l列子矩阵;Sx为Px的Cholesky分解阵,Sξ为Sx的前m行、m列子矩阵,Sη为Sx的后l行、l列子矩阵,Sηξ为Sx的后l行、前m列子矩阵。

证明可借鉴文献[13]的证明思路,按照相同步骤来证明定理2。为了节略篇幅,仅列出主要证明步骤,忽略相关细节。

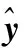
其次,求解Py。对Px做Cholesky分解

将Px和Sx改写成

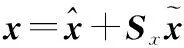
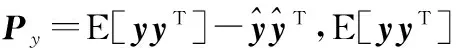
其中

舍弃繁琐的推导步骤,有

则

其中

舍弃中间步骤,得

从而,可以得到

证毕

步骤 1重采样

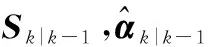
步骤 2观测传播

计算Ti=T(ξi,k|k-1),i=(ξi,k|k-1),hi=h(ξi,k|k-1)。

(19)

步骤 4状态更新

(20)

2.3非线性对准仿真

图1　车辆行驶轨迹图Fig.1　Vehicle driving trajectory

分别设置两组初始失准角[1°,1°,10°]和[3°,3°,20°],使用降维CKF进行对准实验,仿真时间700 s。由于水平对准速度快、精度高,只分析方位对准情况。图2给出了两组实验中方位对准结果,图3给出了对准过程中的水平位置误差。

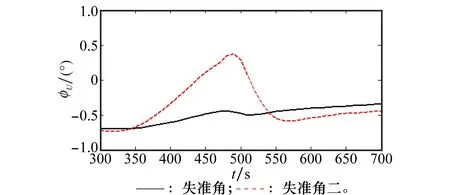
图2　方位对准误差Fig.2　Azimuth alignment error

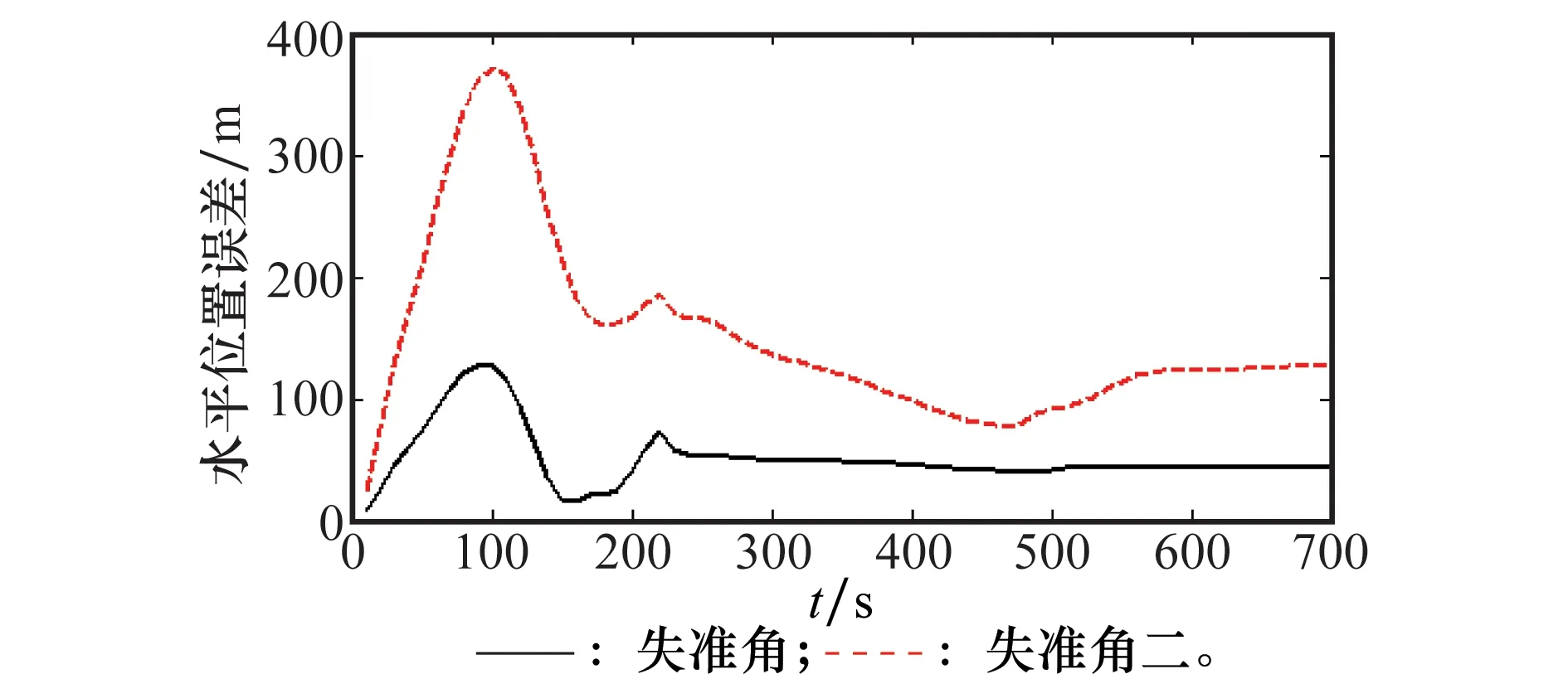
图3　水平位置误差Fig.3　Horizontal position error

3　非线性R-T-S平滑

非线性对准结束时,在此基础上进行SINS/OD组合导航,将带来较大的初始位置误差。应急情况下,可直接使用此对准结果,导航过程中出现其他参考信息时可进行校正。正常工作中,当计算速度较快或有多个处理器时,为了减小位置误差,可借用数据存储和循环解算的思想,利用逆向导航或状态平滑对导航信息进行再处理。为了减小计算量,应用状态平滑。

平滑分为R-T-S平滑[17-18]和TF平滑[19],前者计算量小,原理简单,应用广泛。非线性R-T-S平滑在前向非线性滤波的基础上进行后向递推,获得此前任意时刻状态估计，估计过程如下:

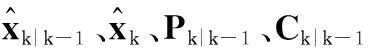
步骤 2后向递推,按照k=N,N-1,…,1的顺序进行递推

(21)

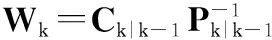
经过后向递推后,获得各时刻的状态平滑估计,由于后向递推利用的观测信息多于前向滤波,估计精度优于滤波。

图4给出了上述仿真实验中第二组实验方位对准的平滑估计结果,可以看出整个平滑过程中,方位失准角为小角度。将SINS/OD非线性对准结果进行后向平滑估计,获得初始时刻失准角估计;此时对系统进行修正,可获得小误差的SINS初始姿态,可将非线性误差模型退化为线性模型。

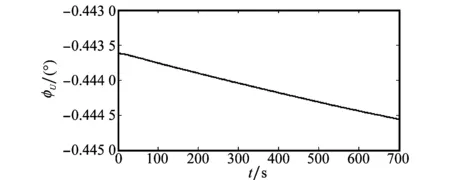
图4　方位平滑估计误差Fig.4　Azimuth alignment smoothing estimation error

4　实验验证

4.1对准算法设置

根据车辆实际情况,设计如下对准方案:

(1) 粗对准

为了在较短时间里获得较好估计效果,非线性对准要求对初始方位失准角进行一定的控制,失准角过大,对准时间变长,无法收敛。在车辆发动下,采集30s左右的数据,进行惯性系粗对准,获得初始姿态。

(2) 降维非线性对准

车辆开始行驶,利用降维CKF进行SINS/OD非线性对准,并存储相关数据(SINS、OD、滤波数据等)。机动一段时间后,完成对准。

(3) 非线性R-T-S平滑

基于存储的滤波数据进行非线性R-T-S平滑,初始时刻进行校正,获得初始姿态。

(4) 再次对准

基于存储的SINS和OD数据,使用小角度线性误差模型和卡尔曼滤波,再次进行对准。

4.2跑车实验

实验室将某型光纤陀螺SINS安装在某战车上,使用战车自身安装OD的输出信号。光纤陀螺的零偏稳定性不超过0.02 (°)/h,加速度计的偏值重复性小于0.05mg。首先需对SINS和OD的安装偏差角、OD标定系数进行初始标定,其中OD输出脉冲当量为 0.011 2米/脉冲。

表1　方位对准结果

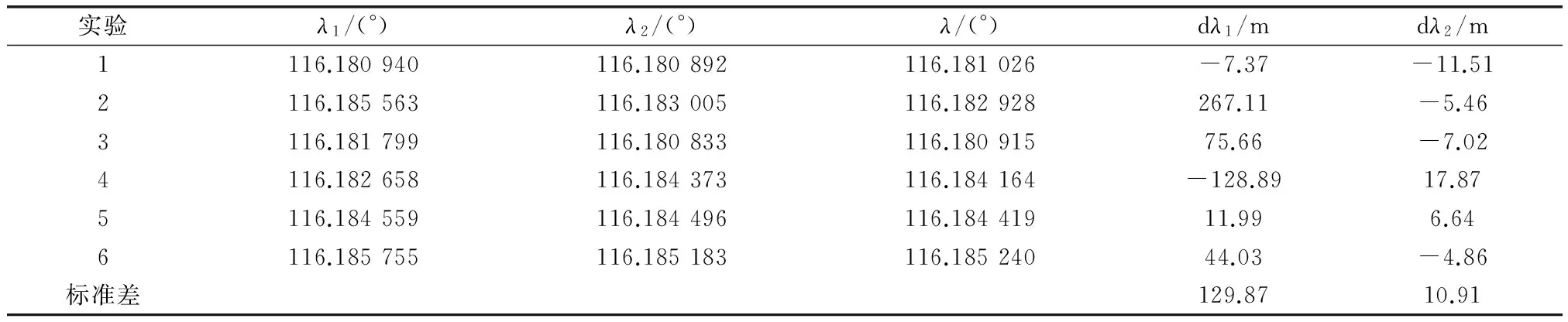
表2　经度误差

表3　纬度误差

非线性对准结束后,方位精度为0.224°,经度误差为129.87 m,纬度误差为143.54 m,对准过程中能够提供相当精度的位置导航。经过R-T-S平滑后和再次线性对准后,方位精度减为0.1°,经度误差为10.91 m,纬度误差为10.01 m,对准精度和位置精度大幅提高。再次对准大大减小了后续SINS/OD组合导航的初始位置误差,继而提高整个导航过程的位置误差。

5　结　论

为了实现SINS/OD动基座对准中的位置导航,设计了“首次降维非线性对准、非线性后向平滑、再次线性对准”的动基座对准方案。该方案对准过程中具备位置导航能力,对准结束后获得高精度的姿态精度和位置精度。该方案严格来说是一种离线方案,而实际应用需使用实时方案。为了实时实现该方案,一种方案是设计双DSP结构。DSP1用来处理前向过程,DSP2用来处理后向平滑和再次对准。当前向非线性对准收敛后,启动DSP2进行平滑和再次对准。由于DSP处理速度较快,DSP2处理时刻最终会赶上DSP1。此时,利用DSP2信息对DSP1进行校正。实际过程中,还需进行进一步研究。

[1] Wu Y X, Wu M P, Hu X P, et al. Self-calibration for land navigation using inertial sensors and odometer: observability analysis[C]∥Proc.oftheAIAAConferenceofGuidance,NavigationandControl, 2009: 1-10.

[2] Georgy J, Karamat T,Umar I, et al. Enhanced MEMS-IMU / odometer/GPS integration using mixture particle filter[J].GPSSolutions, 2011, 15(3):239-252.

[3] Silson P M G. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J].IEEETrans.onInstrumentationandMeasurement, 2011, 60(6): 1930-1941.

[4] Gu D Q, El-Sheimy N, Hassan T, et al. Coarse alignment for marine SINS using gravity in the inertial frame as a reference[C]∥Proc.oftheIEEEPosition,LocationandNavigationSymposium, 2008:961-965.

[5] Yan G M, Qin Y Y, Wei Y X, et al. New initial alignment algorithm for SINS on moving based[J].SystemsEngineeringandElectronics, 2009, 31(3):634-637. (严恭敏,秦永元,卫育新,等.一种适用于SINS动基座初始对准的新算法[J].系统工程与电子技术,2009, 31(3):634-637.)

[6] Yan G M, Yan W S, Xu D M. On reverse navigation algorithm and its application to SINS gyro-compass in-movement alignment[C]∥Proc.ofthe27thChineseControlConference, 2008: 724-729.(严恭敏,严卫生,徐德民. 逆向导航算法及其在捷联罗经动基座初始对准中的应用[C]∥第27届中国控制会议论文集,2008: 724-729.)

[7] Li W L, Wu W Q, Wang J L, et al. A novel backtracking navigation scheme for autonomous underwater vehicles[J].Measurement, 2014, 47: 496-504.

[8] Gao W,Ben Y Y,Zhang X,et al. Rapid fine strapdown INS alignment method under marine mooring condition[J].IEEETrans.onAerospaceandElectronicSystem, 2011, 47(4): 2887-2896.

[9] Liu X X, Xu X S, Wang L H, et al. A fast compass alignment method for SINS based on saved data and repeated navigation solution[J].Measurement, 2013, 46(10):3836-3846.

[10] Li J S, Xu J N, He H Y, et al. Backtracking scheme for alignment with strict reverse process based on compass[J].SystemsEngineeringandElectronics, 2014, 36(2): 348-353.(李京书, 许江宁, 何泓洋,等. 严格逆向过程的罗经回溯对准方法[J].系统工程与电子技术, 2014, 36(2):348-353.)

[11] Arasaratnam I, Haykin S. Cubature Kalman filters[J].IEEETrans.onAutomaticControl, 2009, 54(6): 1254-1269.

[12] Wang S Y, Feng J C, Tse C K. Spherical simplex-radial cubature Kalman filter[J].IEEESignalProcessingLetters, 2014, 21(1): 43-46.

[13] Qian H M, Ge L, Huang W, et al. Reduced dimension CKF algorithm and its application in SINS initial alignment[J].SystemsEngineeringandElectronics, 2013,35(7): 1492-1497.(钱华明,葛磊,黄蔚,等. 降维CKF算法及其在SINS初始对准中的应用[J].系统工程与电子技术, 2013, 35(7):1492-1497.)

[14] Arasaratnam I, Haykin S. Cubature Kalman smoothers[J].Automatica, 2011, 47(10): 2245-2250.

[15] Gadsden S A, Al-Shabi M, Arasaratnam I, et al. Combined cubature Kalman and smooth variable structure filtering: a robust nonlinear estimation strategy[J].SignalProcessing, 2014, 96:290-299.

[16] Yan G M, Yan W S, Xu D M. A SINS nonlinear error model reflecting better characteristics of SINS errors[J].JournalofNorthwesternPolytechnicalUniversity, 2009, 27(4): 511-516. (严恭敏,严卫生,徐德民. 基于欧拉平台误差角的 SINS 非线性误差模型研究[J].西北工业大学学报, 2009, 27(4): 511-516.)

[17] Wang X X, Pan Q, Liang Y, et al. Application of unscented transformation for nonlinear state smoothing[J].ActaAutomaticaSinica, 2012, 38(7):1107-1112.

[18] Jia B, Xin M. Rauch-Tung-Striebel high-degree cubature Kalman smoother[C]∥Proc.oftheAmericanControlConference, 2013: 2472-2477.

[19] Ma Y H, Fang J C, Li J L. Accurate estimation of lever arm in SINS/GPS integration by smoothing methods[J].Measurement, 2014, 48: 119-127.

ResearchonmovingbaseinitialalignmentofSINS/ODwithreduceddimensionCKFandsmoother

HUANGXiang-yuan,TANGXia-qing,WUMeng

(Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

Inordertoimprovethealignmentprecisionofstrapdowninertialnavigationsystem(SINS) /odometer(OD),andtomakeithavethepositionnavigationcapabilitywithacertainprecision,anonlinearalignmentmethodonthemovingbaseisproposed.Firstly,thenonlinearsystemissimplified,andthealignmentiscarriedoutbyusingthereduceddimensioncubatureKalmanfilter(RD-CKF),forthatpositionnavigationcanbeperformedinthenonlinearalignment,andensuringthatthemisalignmentanglesaresmallattheendofthealignment.Then,thenonlinearR-T-Ssmootherisusedtotheinitialtimeforattitudecalibration,andatwicealignmentismadebymeansofKalmanfiltertorealizehighprecisionattitudeandpositionnavigationattheendofthealignment.Theexperimentiscarriedoutinarealvehicletodemonstratetheeffectivenessoftheproposedmethod.

cubatureKalmanfilter(CKF);reduceddimension;initialalignment;R-T-Ssmoother

2015-07-16；

2015-11-17；网络优先出版日期：2016-02-18。

军队计划项目资助课题

U666.1

ADOI:10.3969/j.issn.1001-506X.2016.09.24

黄湘远(1988-),男,博士研究生,主要研究方向为非线性滤波、惯性导航。

E-mail:huangxiangyuan.623@163.com

汤霞清(1965-),男,教授,博士,主要研究方向为惯性导航、战车火控。

E-mail:tangxiaqing_001@163.com

武萌(1981-),女,讲师,博士研究生,主要研究方向为导航、制导与控制。

E-mail:wumeng0326@126.com