下行卫星认知无线电门限与功率联合优化
2016-09-07畅志贤陈思宏李艺霞
陈 鹏, 畅志贤, 陈思宏, 李艺霞
(1. 中国空间技术研究院西安分院, 陕西 西安 710100;2. 西安邮电大学通信与信息工程学院, 陕西 西安 710121)
下行卫星认知无线电门限与功率联合优化
陈鹏1, 畅志贤2, 陈思宏1, 李艺霞1
(1. 中国空间技术研究院西安分院, 陕西 西安 710100;2. 西安邮电大学通信与信息工程学院, 陕西 西安 710121)
用于卫星通信的频谱资源日益紧缺,但现存卫星系统却存在利用不足的问题。针对该问题,以最大化卫星通信中下行带内数据传输量为目标,提出了基于Underlay认知无线电的卫星信道检测门限与功率分配联合优化算法。首先分析了下行链路中信道融合检测误差、功率分配向量与数据传输量之间的数学关系,给出了信道数量及总功率均受限时信道与功率联合分配的可行性条件。之后,进行了目标模型可行性论证及融合误差分析,并将优化目标函数问题分解为检测门限与功率分配两个子优化问题。针对两个子问题,文中分别证明了加窗粒子群优化算法适用于数据融合后的门限优化,论证了信道与功率联合分配的可行性,在此基础上给出了信道与功率联合分配的最优解。引入中间量在两个子优化算法之间反复迭代,得到了本文目标函数的联合最优解。最后,仿真给出了检测门限优化性能,结果表明,改进型算法在准确度和迭代次数上均优于传统粒子群算法;比较了该联合优化算法与传统卫星通信方式及普通Underlay认知无线电用于卫星通信时的性能差异,结果表明,该联合算法能够有效提高频谱利用率;给出了算法复杂度。
卫星通信; 认知无线电;下行链路;检测门限; 功率分配; 联合优化
0 引 言
地面无线网络中经常存在频率利用不充分的情况[1]。不同于地面通信,大气层衰减效应使得卫星通信可用频率更少,资源更显珍贵。即便如此,卫星通信仍未免俗,同样存在频率利用效率低下的问题[2-4],提高频谱利用率显得尤为迫切[5]。
一种有效的解决手段是将认知无线电[6-7]引入卫星通信[8-9],在有限的频谱范围内获取更多的系统数据传输量[10-11]。作者前期工作[12]中,针对卫星通信的上行链路,以最大化频带内的统计数据传输量为目的,提出了一种基于Underlay认知无线电[13]的优化算法,仿真结果表明,该算法可以更为有效地利用卫星上行链路频率资源。然而,卫星通信为双向对等通信,下行链路与上行链路同样重要,缺一不可。本文以最大化下行链路频谱利用率为目标,结合文献[12]中算法使整个卫星通信系统的频谱利用率得到改善。
上、下行链路模型相似之处在于实现Underlay认知无线电的前提条件,即:认知系统(secondarysystem,SSY)发射机对原有系统(primarysystem,PSY)接收机所产生的干扰低于PSY接收机的干扰容限[14]。原有系统中的卫星称为原有卫星(primarysatellite,PS)。
上、下行链路模型不同之处在于信道检测方式和功率约束条件不尽相同:①认知用户(secondaryuser,SU)对PSY下行信道进行探测[15],并通过上行链路反馈给认知卫星(secondarysatellite,SS),由SS进行所有信道信息数据融合,并由SS对PSY信道进行判断,因此判断门限与误检概率之间的关系与上行链路不同;②SS作为发射机向所有SU传送数据,传输功率总和受到星载功率放大器额定功率的限制,而功率受限会造成下行信道数量受限,此时必须考虑对每个用户的信道分配和对每条信道上的功率分配。
本文针对这两个不同之处分别进行建模与分析。对于信道状态判断方法的不同,本文首先对下行链路中判断门限与误检概率之间的关系进行了分析,给出了SU检测端的判断门限与SS数据融合结果之间的关系;之后通过理论证明论证了加窗粒子群算法(windowedparticalswarmoptimization,WPSO)[12]同样适用于下行链路中最优门限的逼近。对于功率限制条件的不同,本文将信道分配与功率分配这两个问题视为一个联合分配问题,首先给出了信道与功率联合分配的可行性条件,通过等价条件的证明,将可行性条件转化为带有约束条件的最优化分配问题,最后根据库恩-塔克条件求出了下行链路中信道与功率联合分配的最优可行解。本文以最大化下行链路频带内统计数据传输量为目的,给出了一种检测门限与功率分配联合优化算法。仿真结果表明,相比于传统方式及一些典型应用方式,本文算法可以更为有效地利用卫星下行链路频率资源。
1 系统建模与目标建立
本文沿用文献[12]中假设条件与参数符号,符号均表示下行链路参数。在模型分析与论证时主要针对上、下行不同之处。
1.1信道分配模型
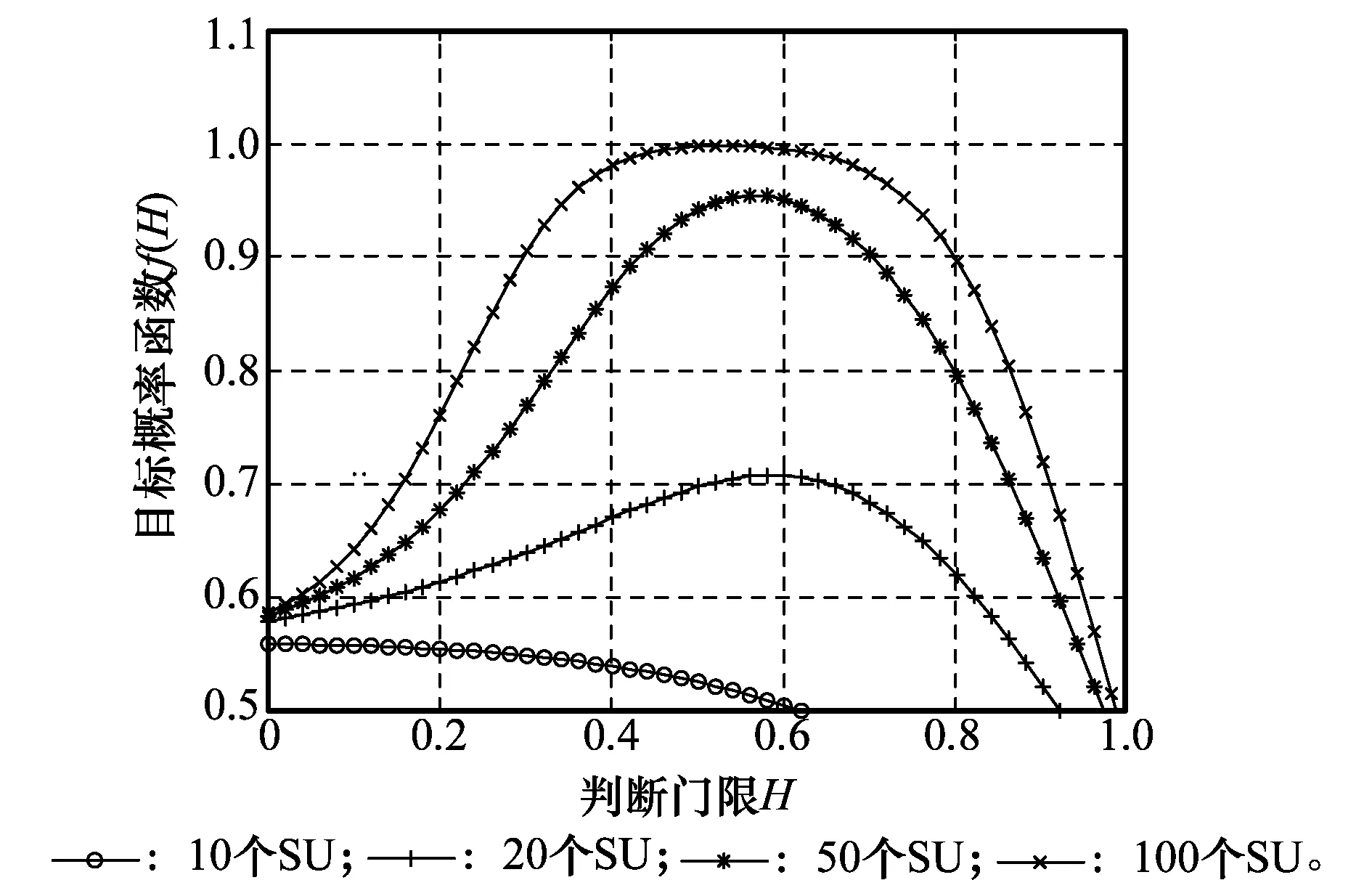
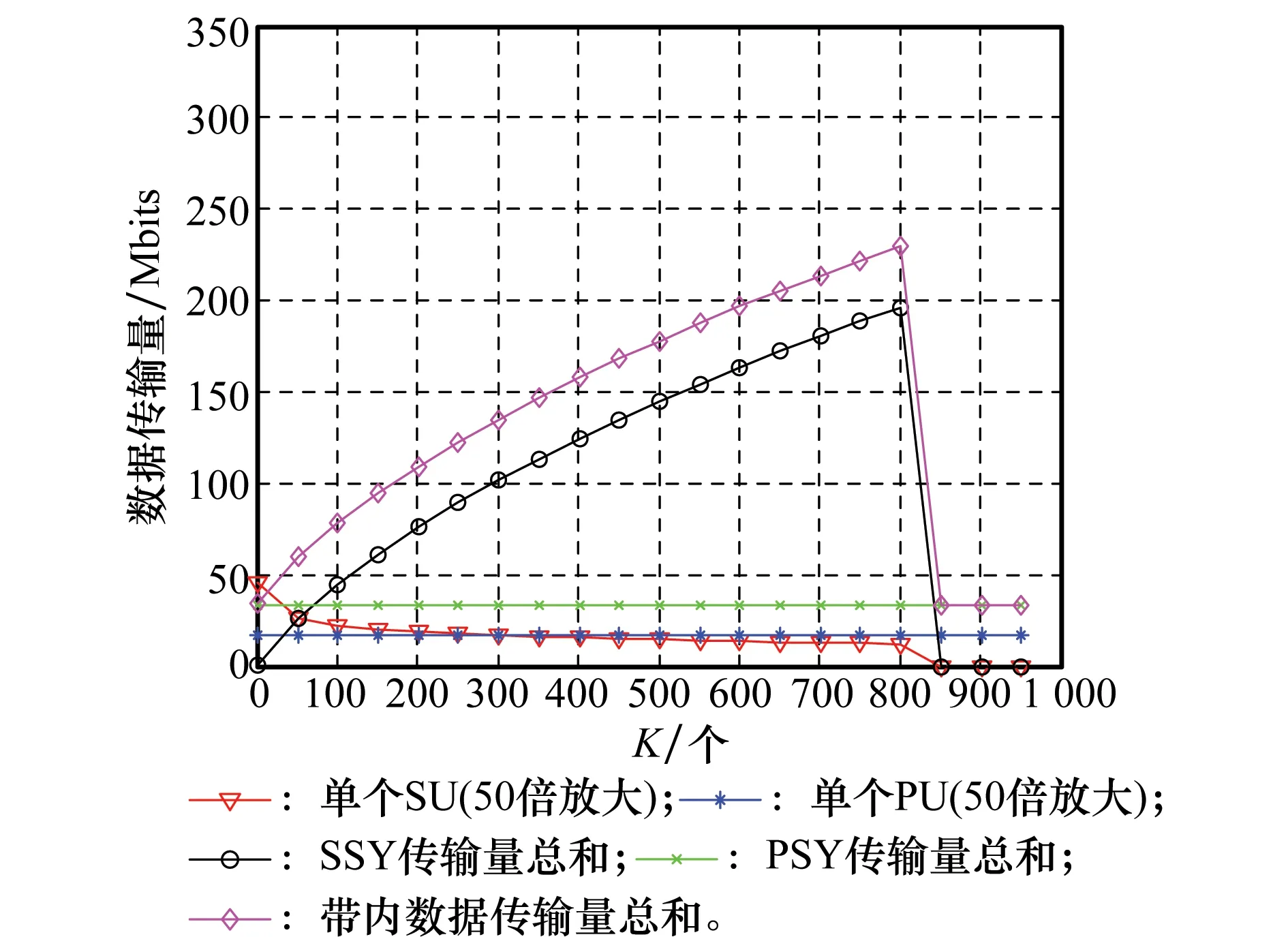
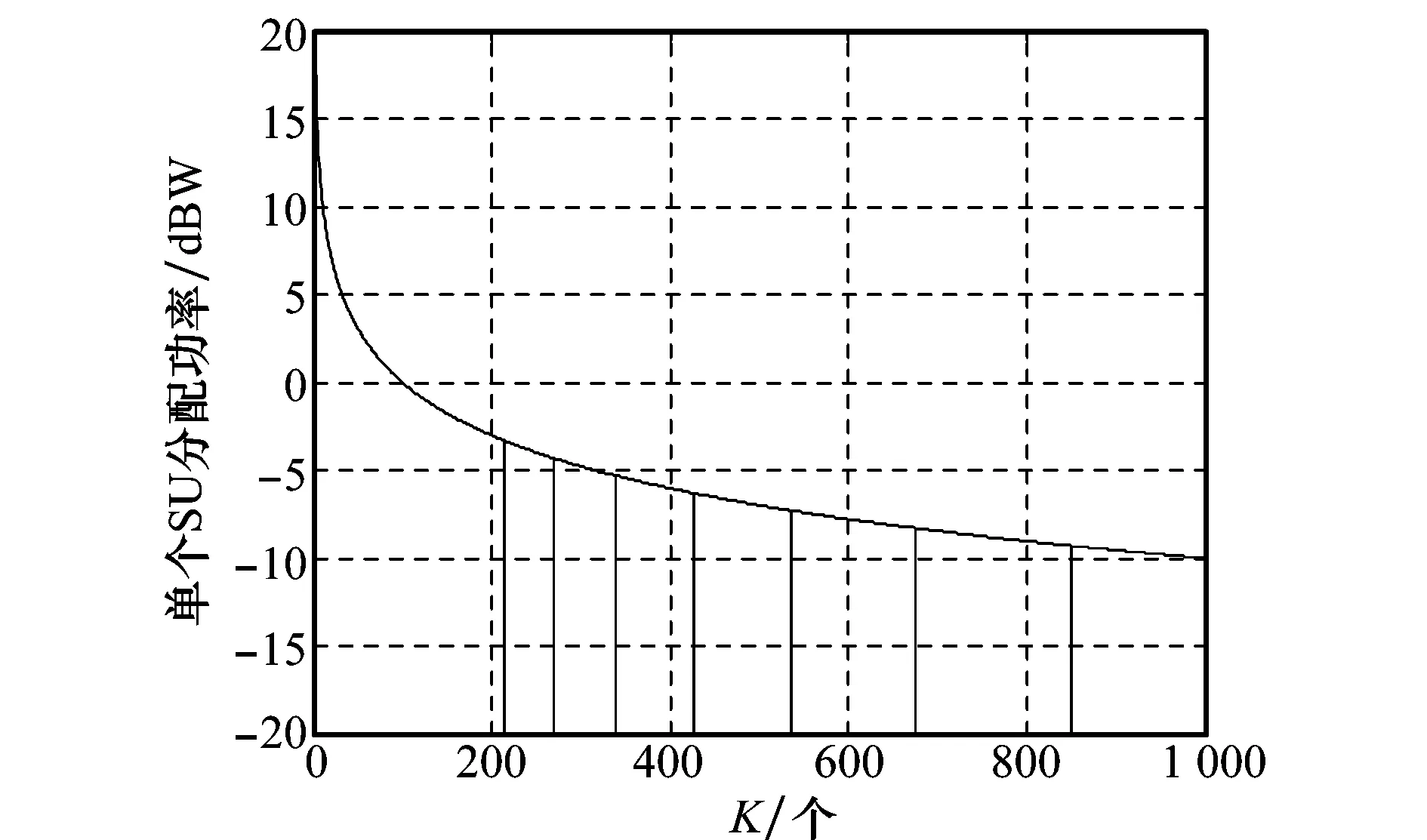
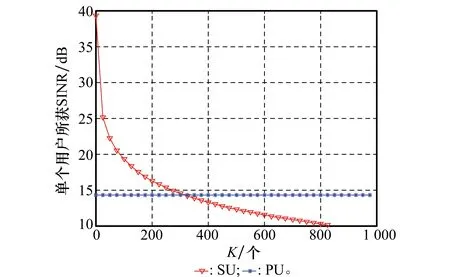
下行链路信道数量有限,假定在某一时间段内的可用扩频码为C个,即可看作此时SSY下行链路具有C条信道。假定下行信道数为C,SU数量为K,每个SU至多只能分配到1个信道,则当C≥K时所有SU均可以分配到信道,当C 于是,可以将下行链路分配问题分解为两个子问题,即C条信道如何分配给K个SU问题和C条信道上的传输功率分配问题。前者用信道分配矩阵X来描述,后者则通过功率控制向量p来说明。其中,X表示用户的信道分配情况,为一个K×C矩阵,若第k个用户被分配到了信道c则X(k,c)=1,否则X(k,c)=0。p为C元素向量,每一个元素pc代表了对应信道上分配的功率。 1.2信道分配的可行性条件 由于发送功率有限,同时须满足PSY与SSY的通信需求,可行性判断必不可少。 C1∀k∈(1,K),c∈(1,C),不存在c1≠c2使得X(k,c1)=X(k,c2),即每个SU至多分配一条信道;且不存在k1≠k2使得X(k1,c)=X(k2,c),即每个信道至多分配给一个SU; 1.3功率限制建模 根据信号功率、干扰功率和噪声功率之间的关系,每条PU下行链路上的SINR可描述为 (1) (2) (3) s.t. (4) (5) 当第k个SU被分配到第c条信道上时,即X(k,c)=1,则必须满足式(4);当第k个SU没有分配到信道时,rk=0。 (6) s.t. (7) (8) (9) 为计算简便,同样取文献[4]中数据传输量的定义式Tk=ln(1+rk),则下行链路最大化目标函数为 (10) 1.4检测误差建模 (11) 假定SUk对第n条信道漏检概率为Q(0|1),虚警概率为Q(1|0),k∈[1,K],n∈[1,N]。各SU的检测门限均为Hth,则 (12) 星载处理器融合所有SU提交的信息后对整个频段上信道占用状况进行判断,得到对信道n的检测概率为 (13) 漏检概率为 (14) 虚警概率为 (15) 在仅存在漏检时,Γ是根据a1条检测信道计算得出,即取a1条检测信道中干扰上限最小者作为Γ,其中a1∈{0,1,…,m-1}。假定漏检信道中干扰上限与检测信道中干扰上限独立同分布,此时m-a1条漏检信道中干扰上限是所有PU信道中干扰上限最小者的概率为 (16) 则由漏检引起干扰上限发生错误的概率为 (17) 在仅存在虚警时Γ是根据a2条检测信道计算得出,对虚警的a2-m条信道中干扰上限是所有PU信道中干扰上限最小者的概率为 (18) 则由虚警引起干扰上限发生错误的概率为 (19) 根据上述内容,定义各类事件及其发生概率。 准确感知事件:SSY对检测准确,此时可以最大化SSY吞吐量,该事件发生概率为 (20) 虚警感知事件:Γ的取值小于PSY实际干扰上限,以η∈(0,1)表示Γ与实际PSY干扰上限之间的比例系数。假设η服从[0,1]区间上的均匀分布,则该事件发生时,数据量与事件发生概率分别为 (21) (22) 漏检感知事件:SSY估计出的Γ大于PSY干扰上限而使PSY无法正常通信,PSY与SSY的数据传输量均为0,发生概率为 (23) 1.5目标描述 根据数学期望的定义、信道分配可行性定义和概率事件分析结果,SU的功率控制问题便转化为在式(25)~式(29)约束下求解式(24)的最优化问题。 (24) s.t. (25) (26) (27) (28) (29) 式中 (30) 建立式(24)~式(30)所述模型后,为获得可行的联合最优解,首先应该论证符合模型中限制条件的解是可行的,之后才可在限制条件的约束下求解该模型的最优解。 2.1可行性论证 通过下面两个命题的证明,不难看出策略可行性与限制条件之间的充要关系。 证明由可行性条件C1可知式(25)、式(26)成立;由可行性条件C3可知,式(27)成立;由可行性条件C4可知,式(28)成立;将式(2)代入式(30),再由条件C4可知,式(29)成立。 证毕 再将式(26)代入式(28)可得 因此条件C4成立。 证毕 可以看出,在式(25)~式(29)的限制下求解式(24)所得的信道功率联合分配策略是最大化SSY吞吐量的可行策略。 2.2D-JDPO策略 求解带有限制条件的式(24)是多变量并行最优化问题,过程复杂,不利于卫星实现,且任意参数改变导致算法重新运行。 本文算法,即下行检测门限与功率联合最优算法(downlink joint detection & power optimization, D-JDPO)以模型中概率参数为切入点,对其初步优化后,结合各参数间的关系以及限制条件对信道分配参数优化,更新中间变量并再次优化概率参数,经过反复迭代最终实现系统参数最优化。此做法的好处在于将庞大的并行计算转换为串并结合的迭代计算,且任意参数改变只需更新中间变量。 2.2.1信道分配 对星载处理器而言,当前对下行信道的分配状态可以用C维向量φ表征,φ中元素φc表示为 (31) 式中,φc表示第c条信道是否被分配到某个SU;1表示已分配;0表示未分配。假设SS能够获得各个SU反馈的信道信息,且卫星依照先申请先分配的原则向SU提供下行链路。定义Z=min(C,K),则在当前时刻前Z条信道已被分配,具体表示为 (32) 结合第1.1节内容,无论C与K的关系如何,前Z条信道状态均为已分配,具体表示为 (33) 此时,根据数学期望的定义式,式(24)中最大化目标函数可描述为 (34) 可将式(34)写为 (35) (36) (37) 为使式(34)最大化,需要考虑两个方面:其一为通过最大化E(T)对检测门限做出最优选择,其二为寻找使E(T)最大化的功率分配向量。 2.2.2下行链路中的WPSO论证 采用与文献[4]相同的思路,给出下行链路中门限优化目标函数为 max[f(H)]= (38) 下行链路中WPSO算法论证如下。 命题 3在本文场景中,以若干固定点均匀地将门限取值区间平分为数个子区间,在所有固定点中能使f(H)取值最大的点记为s,则f(H)全局最大值必取自于s相邻的两个子区间内。 证明假定与s相邻的两个固定点分别为s1、s2,且s1 证毕 通过命题3的证明可以看出,WPSO同样适用于下行链路,其具体步骤如下: 步骤 1将βz赋初值并带入目标函数式(38),其后每次迭代后根据功率子算法实时更新βz; 步骤 2本文利用9个固定点将门限取值区间平均分为10个子区间,并取窗宽为0.2; 步骤 3求出9个散落点的目标函数,找出其中最大值,将最大值对应的固定点作为窗的中心,以步骤2中窗宽加窗; 步骤 4在窗内进行PSO搜索,寻找使f(H)最大的点Hopt,直至满足优化精细度的要求,分别计算qd,ql,qo。 2.2.3功率分配优化 根据前述限制条件,式(24)中的功率分配问题可以细化为 (39) (40) s.t. (41) (42) (43) (44) 可以看出目标函数为凸函数,而其约束条件式(41)~式(44)均为线性函数,满足凸函数定义,因此满足Kuhn-Tucker条件的功率分配向量p是式(39)取最大值的充要条件。对于满足Kuhn-Tucker条件的最优功率分配向量p通常以构造拉格朗日函数对其求解。由于求解过程与U-JDPO算法类似,因此此处仅给出如式(45)所示的拉格朗日函数,求解出的最优功率向量p如式(46)所示。 (45) (46) (47) (48) (49) 综合门限优化与功率分配优化,给出下行最优联合(D-JDPO)算法的实现具体步骤,如下: 步骤 1初始化βz; 步骤 2将βz代入并以改进型粒子群算法逼近式(38),得出qd、ql; 假设PS通信参数分别为:路径损耗-210 dB,额定发送功率100 W,发送天线增益Gt=30 dB,接收天线增益Gr=40 dB,接收机噪声温度为24.3 dBK, PU之间ρ=0。假设每个用户在注册频率内分配带宽b=100 kHz,注册带宽B为100 MHz,假定PU的SINR最小取14 dB才能满足QoS要求。 3.1不同算法数据传输量比较 作为比较,本次仿真给出不带门限检测的普通Underlay认知无线电用于卫星信道与传统卫星通信方式两种情况的数据传输量。其中传统卫星通信采用固定的信道、功率分配模式;不带门限检测的Underlay认知无线电分两种方式:SSY依据全部PSY信道计算,SSY依据PSY中具有大信号的信道计算。以SU数量为自变量,数据传输量的数学期望为因变量,考察5种方法的频谱使用效率,如图1所示。 图1 不同下行通信方式的数据传输量比较Fig.1 Comparison of throughput among different downlink communication methods 与上行链路不同,在下行链路中,将Underlay认知无线电引入PSY能够直接提升系统数据传输量性能。以全信道计算Γ时,不存在漏检现象,Γ取全部信道中的最小值,此时SSY对PSY的干扰最低,同时具有最高的可靠性和最低的有效性;以大信号信道计算Γ时,能够获得最大的SSY传输功率,然而由漏检引起的双方系统中断概率亦为最大,同时具有最高的有效性和最低的可靠性;统计而言,全信道计算Γ情况的数据传输量多于大信号信道情况。D-JDPO以提高带内总数据传输量的期望为目的,对可靠性与有效性两方面联合优化,在统计上具有最多的数据传输量。 图1中在SU个数超过830后,SSY的数据传输量归于0。下行链路中卫星发送总功率不变,SU越多则每个用户分配的功率越小。当SU数量过多时,每个用户分配的功率过小,不足以满足其QoS所需的最小SINR要求,此时所有SU无法通信而造成了传输功率为0。 注意到本例中,K的最大取值为830,即SU数量最多不能超过830个,小于扩频信道数量,满足K 3.2最佳门限逼近性能 本次仿真通过50次蒙特卡罗试验,分别用传统PSO算法和WPSO算法对目标函数在不同情况下的实际曲线进行逼近,目标函数曲线如图2所示。在50次仿真结果中,将均值、方差和检测次数作为指标,所获最优门限与对应f(H) 最优逼近的指标性能如表1与表2所示。不难看出两种方法对目标函数最大值逼近均可满足误差要求。但就两者比较而言,以方差作为参数衡量两种算法检测误差时,WPSO算法在整体效果上好于传统PSO方法;在完成检测所需的迭代次数上,WPSO算法明显优于传统PSO算法。关于计算复杂度进一步讨论见第3.4节。 图2 目标函数的实际曲线Fig.2 Practice curve of interested function 表1 传统PSO算法所获性能 表2 WPSO算法性能 3.3功率分配性能 3.3.1数据传输量细节分析 选取PU数量为100,对SU及PSY进行仿真分析,所得到的结果比较如下。 图3 SU数量与数据传输量的关系Fig.3 Relationship between number of SU and throughput 图4 D-JDPO在SU不同扩频增益下的性能比较Fig.4 Comparison of performances of D-JDPO under deferent spreading gains of SU 3.3.2用户数量及分配功率分析 (50) 图5 D-JDPO中SU数量与单个SU分配功率的关系Fig.5 Analysis of D-JDPO on relationship between SU number and power allocation on per SU 在PU与SU最小SINR分别为14dB和10dB时,两者实际得到的SINR如图6所示。与上行信道不同,SU的接收SINR下降趋势明显,而PU的SINR下降不明显,甚至维持不变。这是由于在下行信道中,卫星发射机最大发送功率保持不变,当SU数量增长至一定程度后,每个SU因为得不到要求的SINR而使SSY无法正常工作,即便SSY卫星以全功率进行数据发送时,SU也不能获得相应的SINR。而PU受到的干扰来自SS的发送功率,可以维持SINR不变。 图6 各个用户SINR分析图Fig.6 Analysis of SINR of each SU 3.4复杂度分析 算法计算量关系着实现复杂度,通过文中联合优化算法的完成步骤不难了解完成该算法所需的计算量。在优化检测门限的单次迭代中,传统PSO与WPSO通过式(38)对目标函数完成一次运算均需要ο[m2+(N-m)2]次乘法,ο(N)次加法运算,单次WPSO迭代较传统PSO多进行一次粒子比较,此过程需要的加法、乘法和比较运算次数均为ο(M)。本文中取M=9,结合第3.2节中表1、表2不难看出,WPSO较之传统PSO算法,以少量的附加计算大幅降低了迭代次数,将迭代次数从7~9次降至3次。WPSO所需要总的计算量为ο(N+M)次加法、ο[m2+(N-m)2+M]次乘法和ο(M)次比较运算。 在优化功率分配的单次迭代中,式(49)中Y可通过一次比较运算完成,之后按照式(40)与式(49)进行迭代计算,pz单次迭代中所需加法与乘法运算均为Z+2次,az所需的乘法和加法运算均为Z次。仿真结果表明,在迭代次数不超过10次时即可达到要求,因此算法实际完成单个SU功率分配所需计算量为ο[20(Z+1)]次加法运算、ο[20(Z+1)]次乘法运算和一次比较运算,完成Z个SU功率分配所需计算量为ο[20Z(Z+1)]次加法运算、ο[20Z(Z+1)]次乘法运算和Z次比较运算。更新βz则需要Z(4Z+5)次乘法运算、Z(4Z+2)次加法运算及2Z次对数运算。 综上,通过文中算法完成单次检测门限与功率分配的联合优化迭代所需计算量为ο{3(m2+(N-m)2+M)+20Z(Z+1)}次乘法运算、ο[3(N+M)+20Z(Z+1)]次加法运算、ο(3M+Z)次比较运算和2Z次对数运算。当SU数量增加时,计算量随之增长,但是若所有SU所需的SINR和最大发送功率相同时,只需对单个SU进行计算则可以完成对所有SU的功率分配。 本文对下行链路中注册频段内数据传输量的最大化展开了研究,通过比较给出了下行链路与上行链路不同之处。之后针对上、下行链路的不同之处对下行链路进行了建模。与上行链路模型不同的是,除了功率分配与检测门限之外,在下行链路模型中,由于信道数量的限制,还需要强调模型与策略的可行性。为此证明了可行性条件与本文模型之间的等价关系。 针对本文模型中的多参数联合优化,通过对信道分配与功率分配的联合优化和下行链路WPSO论证给出了下行链路的最优联合迭代算法。最后仿真并比较了本文算法与目前主要方法的性能差异,分析了门限逼近算法性能,讨论了系统对SU的容纳能力,给出了SU数量对PU及双方系统的影响。仿真结果表明,WPSO在下行链路中同样优于传统PSO算法;相比于其他方法,本文联合算法能够获得最多的带内数据传输量,换言之,能够有效提高频谱使用率。 [1]FederalCommunicationCommission,SpectrumPolicyTaskForce.Reportofthespectrumefficiencyworkinggroup,FCC02-155[R].US:FederalCommunicationCommission, 2002. [2]ShreeKS,SymeonC,BjornO.Cognitiveradiotechniquesforsatellitecommunicationsystems[J].IEEE Trans.on Communication, 2013, 21(6):781-790. [3]ShreeKS,SymeonC,BjornO.Satellitecognitivecommunications:interferencemodelingandtechniquesSelection[C]∥Proc.of the 6th Advanced Satellite Multimedia Systems Conference and 12th Signal Processing for Space Communications Workshop,2012:111-118. [4]MarkoH,JukkaK,AriH,etal.Applicationofcognitiveradiotechniquestosatellitecommunication[C]∥Proc.of the IEEE International Symposium on Dynamic Spectrum Access Networks, 2012:540-544. [5]BiglieriE.Anoverviewofcognitiveradioforsatellitecommunications[C]∥Proc.of the IEEE First AESS European Conference on Satellite Telecommunications, 2012:1-3. [6]MitolaJIII,MaguireGQ.Cognitiveradio:makingsoftwareradiosmorepersonal[J].IEEE Personal Communications, 1999, 6(4):13-18. [7]HaykinS.Cognitiveradio:brain-empoweredwirelesscommunication[J].IEEE Journal on Selected Areas in Communication, 2005, 23(2):201-220. [8]VassakiS,PoulakisMI,PanagopoulosAD,etal.PowerallocationincognitivesatelliteterrestrialnetworkswithQoSconstraints[J].IEEE Communication Letters, 2013, 17(7): 1344-1346. [9]MaL,ChenXT,LiuHJ,etal.TheapplicationanalysisofcognitiveradiotechnologyinLEOsatellitesystems[J].Telecommunication Technology, 2010(4): 49-51.(马陆,陈晓挺,刘会杰,等. 认知无线电技术在低轨通信卫星系统中的应用分析[J].电信技术,2010 (4):49-51.) [10]XuD,FengZY,ZhangP.Effectivecapacityofdelayquality-of-serviceconstrainedspectrumsharingcognitiveradiowithoutdatedchannelfeedback[J].Science China (Information Science), 2013, 56(6):1-9. [11]MusavianL,AissaS.Effectivecapacityofdelay-constrainedcognitiveradioinNakagamifadingchannels[J].IEEE Trans.on Wireless Communication, 2010, 9(3): 1054-1063. [12]ChenP,QiuLD,WangY.Jointoptimizationalgorithmofdetectionthresholdandpowerallocationforsatelliteunderlaycognitiveradio[J].Journal of Xi’an Jiaotong University, 2013,47(6):31-36.(陈鹏,邱乐德,王宇.卫星认知无线电检测门限与功率分配联合优化算法[J].西安交通大学学报,2013,47(6):31-36.) [13]GoldsmithA,JafarSA,MaricI,etal.Breakingspectrumgridlockwithcognitiveradios:aninformationtheoreticperspective[J].Proceedings of the IEEE, 2009, 97(5): 894-914. [14]TadrousJ,SultanA,NafieM.Admissionandpowercontrolforspectrumsharingcognitiveradionetworks[J].IEEE Trans.on Wireless Communications, 2011, 10(6): 1945-1955. [15]XuD,FengZY,LiuY,etal.Outageprobabilityminimizingjointchannelandpowerallocationforcognitiveradionetworks[J].IEEE Electronics Letters, 2011,417(25):1402-1404. [16]YucekT,ArslanH.Asurveyofspectrumsensingalgorithmsforcognitiveradioapplications[J].IEEE Communications Surveys and Tutorials, 2009, 11(1):116-130. Downlinkjointoptimizationofdetectionthresholdandpowerallocationforsatellitecognitiveradio CHENPeng1,CHANGZhi-xian2,CHENSi-hong1,LIYi-xia1 (1. China Academy of Space Technology(Xi’an), Xi’an 710100, China; 2. School of Telecommunication and Information Engineering, Xi’an University of Posts and Telecommunication, Xi’an 710121, China) Thefrequencyresuorceforsatellitecommunicationbecomesrarewhilespectrumutilizationisinefficient.Toraisesuchaspectrumutilizationefficiency,ajointoptimizationofdetectionthresholdandpowerallocationbasedonUnderlaycognitiveradioisproposed.Firstly,themathematicalrelationshipamongdetectionfusionerrors,powerallocationvectorsanddatathroughputisanalyzed.Correspondingly,feasibilityconditionsforjointallocationofchannelandpowerareshownwiththelimitedofchannelnumberandtransmissionpower.Afterfeasibilityargumentationandfusionerroranalysis,thejointoptimizationisdividedintodetectionthre-sholdoptimizationandoptimalpowerallocation.Thesuitabilityofwindowedparticleswarmoptimizationforthedownlinkdetectionthresholdisproved.Theoptimalsolutionofjointallocationofchannelandpowerisfoundtheoreticallybasedonthefeasibilitydiscussionresult.Togetthejointoptimizationofdetectionthresholdandpowerallocation,anintermediatevariableisintroducedwhichperformsiterationbetweentwosub-arithmeticrepeatedly.Simulationresultsshowthesuperiorityoftheproposedwindowedparticleswarmoptimizationovertraditionalmethodsintemsofaccuracyanditerationtimes.Comparingtheperformanceamongthecommonsatellitecommunication,Underlycognitiveradioandthejointoptimization,thecomparisonresultsdemonstratethethroughputimprovementofthejointoptimization.Thecomputationcomplexityisalsopresented. satellitecommunication;cognitiveradio;downlink;detectionthreshold;powerallocation;jointoptimization 2015-05-11; 2015-12-20;网络优先出版日期:2016-07-03。 国家自然科学基金(61471294);国家预研基金(9140A21040114H705336);陕西省自然科学基金(2014JM8320);陕西省科技厅工业攻关项目(2014K09-14);陕西省科技厅国际合作项目(2014KW02-02)资助课题 TN927.23 ADOI:10.3969/j.issn.1001-506X.2016.09.28 陈鹏(1981-),男,工程师,博士,主要研究方向为航天器通信。 E-mail:ertiao9912@gmail.com 畅志贤(1981-),女,讲师,博士研究生,主要研究方向为移动通信。 E-mail:sallychang@163.com 陈思宏(1981-),女,高级工程师,硕士,主要研究方向为空间通信。 E-mail:chensh_xjtu@hotmail.com 李艺霞(1967-),女,高级工程师,硕士,主要研究方向为空间通信。 E-mail:yixiali2013@163.com 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160703.1418.012.html
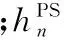


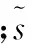
2 信道检测与分配联合优化
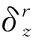
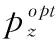
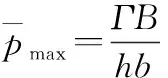
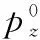
3 性能分析
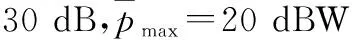



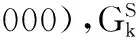

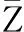


4 结 论
