基于自适应EKF的BDS/GPS精密单点定位方法

赵　琳, 张胜宗, 李　亮, 王　雪

(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)



基于自适应EKF的BDS/GPS精密单点定位方法

赵琳, 张胜宗, 李亮, 王雪

(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)

为使精密单点定位(precise point positioning,PPP)获得更短的收敛时间和更高的定位精度,多个导航系统的集成(例如北斗卫星导航系统(Beidou navigation satellite system,BDS)与全球定位系统(global positioning system,GPS)的组合)和更优的定位方法是两种可行选择。针对传统最小二乘(least square,LS)法解算孤立各历元观测量之间的关系以及扩展卡尔曼滤波(extended Kalman filter,EKF)解算先验信息不准的问题,在PPP中,运用自适应扩展卡尔曼滤波(adaptive extended Kalman filter,AEKF)对过程噪声进行调整,以达到对系统状态的最优估计。文章通过实测数据对算法进行了分析和验证,测试结果表明,与传统的EKF算法相比,基于AEKF算法的PPP收敛速度可提高9 min,定位精度可提高33.7%。

精密单点定位; 收敛时间; 定位精度; 自适应扩展卡尔曼滤波

0　引　言

精密单点定位(precise point positioning,PPP)技术指针对单台接收机的载波相位观测值,分别利用国际GNSS服务(international GNSS service,IGS)所发布的精密卫星轨道与精密卫星钟差等产品,以及其他误差修正模型对多种主要误差源进行改正来实现绝对定位的方法[1]。

目前PPP技术应用较为广泛,基于伪距与载波相位观测数据,其静态数据最终定位结果达到厘米级[2],相关技术已经比较成熟。文献[3]利用9个参考站模拟基于北斗的动态定位,其结果显示仅利用北斗系统的PPP，其定位精度可以达到分米级。但是,目前针对北斗卫星导航系统(Beidou navigation satellite system,BDS)与全球定位系统(global positioning system,GPS)组合的PPP研究相对较少,组合BDS/GPS系统进行PPP,不仅能够增加观测卫星数,提高量测冗余度,而且,较之单一系统,组合系统定位的可靠性、连续性、精度都有了显著的改善。随着全球导航卫星系统(global navigation saiellite system,GNSS)的现代化进程,双系统甚至多系统联合定位已经成为一种趋势。通过组合可以充分发挥各系统的优势,解决单系统在观测条件不佳时可用卫星数不足的问题,以提高定位的连续性[4]。

最小二乘(least square,LS)和扩展卡尔曼滤波(extended Kalman filter,EKF)是实现PPP两种传统的方法,其中传统的LS解算方法,算法简单有效,但由于忽略了各历元之间的关系,尤其是在高采样率的条件下,短时间内空间信号误差存在较强的相关性[5]。由于忽略了历元之间的相关信息,传统LS方法需要更长的时间完成定位收敛的过程。卡尔曼滤波是在线性无偏最小方差估计原理下推出的一种递推滤波方法[6]。然而,传统基于EKF的PPP方法大都采用经验模型设置滤波先验状态误差协方差阵[7-8],实际在动态定位的情况下,先验信息很难与真实的导航状态相匹配,导致定位需要很长的时间才能收敛。而在自适应扩展卡尔曼滤波(adaptive extended Kalman filter,AEKF)算法中,对过程噪声和量测噪声的估计可以优化滤波算法的性能。系统过程噪声和量测噪声作为系统的主要先验信息,对卡尔曼滤波的估计性能和稳定性有着重要的意义,对于两者估计不准确,可能会导致有偏估计,甚至滤波发散[6]。来源于真实量测信息的新息数据,对于卡尔曼滤波性能的评估而言具有重要的意义[9],通过新息方差对过程噪声和量测噪声实时估计和调整,从而更好适应外界环境变化所引起的噪声统计特性的不一致性,使得滤波器具有更佳的收敛性能[9]。使用AEKF能够避免先验信息估计不准对卡尔曼滤波性能的影响,可以进一步提高PPP定位的收敛时间和精度。

由于动态导航环境对传统卡尔曼模型的扰动,以及过程噪声和量测噪声的变化等因素的影响,制约了传统卡尔曼滤波应用的普适性[10]。通过采用极大似然准则下的AEKF算法,对系统的过程噪声进行实时的估计和调整,使得滤波器可以对于系统噪声统计特性的变化做出最优化的适应。针对BDS/GPS组合系统,对这种自适应滤波算法进行了分析。实测计算结果证明该算法的有效性和可行性。

1　组合精密单点原理与技术分析

1.1观测方程及误差处理

卫星导航定位中基本的观测方程为

(1)

(2)

式中,φ、P分别为载波相位以及测码伪距观测量;ρ为用户与卫星之间真实的几何距离;c为电磁波在真空中的传播速度;dtr、dts分别为接收机钟差以及卫星钟差;I为电离层延迟误差;T为对流层延迟;dorb为卫星轨道误差;dtid为潮汐误差;drel为相对论效应误差;N为整周模糊度;dant为天线相位误差;dphw为相位缠绕误差;εφ为载波相位观测噪声和多路径误差;εP为伪距观测噪声和多路径误差。

实际应用中,根据电离层介质的弥散性质,采用双频观测值消除电离层折射影响[11]。考虑组成L1、L2(B1、B2)频率上的线性组合的观测值,其组合系数α1、α2满足:

(3)

式中,f1、f2分别为载波L1、L2(B1、B2)的频率。原则上,α1、α2可以是任意一组满足式(3)的值。但在实际应用中,经常选择[12]

(4)

由此,可以利用双频观测值消除电离层影响。通常使用无电离层组合(ionosphere-free,IF)观测值,组合观测量如下:

(5)

(6)

式中,φIF、PIF分别为无电离层组合载波相位和伪距观测值;NIF为组合整周模糊度;νφ、νP分别为无电离层相位和伪距组合观测噪声,此外

(7)

(8)

式(7)和式(8)中所涉及误差处理方法如表1所示。

表1　PPP误差处理方法

在对各部分误差进行处理后,可以得到修正后的IF组合载波相位观测值和伪距观测值:

(9)

(10)

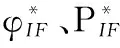
1.2参数估计方法

在上述对PPP各部分误差进行相应的处理后,PPP的估计参数有接收机三维位置、三维速度(动态)、接收机钟差、接收机频漂、对流层湿分量延迟、组合模糊度。滤波处理中选取的状态向量为

(11)

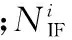
表2　状态处理方法

选取的量测量为每颗可视卫星的IF组合载波相位与伪距观测值:

(12)

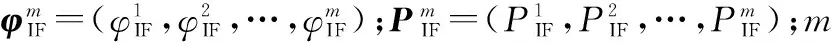
然后对系统进行建模,考虑到系统的非线性,需要先将滤波方程线性化,其中,量测方程非线性,系统模型表示为

(13)

(14)

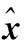
(15)

其中

(16)

其中

(17)

令

(18)

(19)

则将非线性量测函数式(14)一阶线性化后得到量测方程为

(20)

至此,可以得到线性化的系统模型式(13)和式(20),其中状态转移阵Φ和量测阵H可表示为

(21)

式中,I表示单位阵。静态模式时A=03×3,B=03×3,C=[1,0;0,0];动态模式时A=TsI3×3,B=I3×3,C=[1,Ts;0,1],Ts是状态方程的差分步长,在这里也等于测量过程的采样时间间隔。

(22)

式中,G3×k=(lk,mk,nk)(k=1,2,…,m)表示接收机到卫星的观测向量的方向余弦矩阵;I表示单位阵;E=[I1×m,01×m,I1×m,01×m];M1×m=(M1,M2,…,Mm)表示对流层湿分量映射函数矩阵。

在得到由精密星历文件计算的卫星位置误差方差,由精密钟差文件计算的卫星钟差误差方差,IF组合观测噪声方差以及对流层误差方差之后,可以较为准确地得到量测噪声方差阵。此外,同时对过程噪声和量测噪声进行调整的AEKF算法,容易导致滤波发散及滤波过程不稳定[6]。因此，下面所推导的自适应过程仅对过程噪声进行调整估计。

本文运用基于极大似然准则的AEKF对系统状态进行估计,极大似然准则综合新息以及新息协方差的变化,使其能够适应模型扰动以及噪声统计特性变化的影响[13]。已知系统的线性模型如式(13)和式(20)所示,基于参考文献[6]可以计算自适应过程下的过程噪声为

(23)

式中,N为平滑窗口宽度;Δx为状态更正量;P为估计误差方差阵。

2　数据处理与分析

为充分验证所提出算法的性能,通过静态和动态PPP实验进行了测试。需要指出的是,测试过程中,BDS和GPS精密星历与精密钟差数据分别由中科院测地所和IGS中心提供,更新时间分别为15 min和5 min。

在对数据进行处理时,还应考虑各个观测值的权重大小,权重表示了各个观测值对整个解的贡献大小,正确匹配权值才能获得最优的结果,这其中涉及的以卫星高度角定权的一种随机模型形式为

(24)

(25)

在滤波过程中,由式(23)可知在估计过程噪声Q时涉及到Δx项,从而直接反映系统的状态变化,由此可见,准确地估计过程噪声将会使得滤波器更好地跟踪动态条件系统状态的变化情况。所以在数据处理中,必须恰当地选择平滑窗口的宽度N,为此,测试时对N进行了不同的取值,取N从50开始,按步长50增加,通过比较分析可知,当窗口宽度N取200时,状态估计误差精度达到最高。

2.1静态模式

为测试静态条件下BDS/GPS组合系统及单系统PPP的效果,采用澳大利亚CUT0站2014年6月17日的数据进行定位解算,其接收机为Trimble Net R9,该观测数据采样率为30 s,截止高度角设为15°。在AEKF处理过程中,BDS和GPS载波相位观测量的观测噪声标准差均设为0.003 m,伪距观测量的观测噪声标准差分别设为0.6 m和0.3 m。

本文分别对BDS单系统,GPS单系统,BDS/GPS组合系统3种情况进行AEKF数据处理。以XYZ三方向的位置误差(分别用errorX、errorY、errorZ表示)均达到10 cm以内定义滤波收敛。对BDS/GPS组合系统分别应用LS、EKF、AEKF 3种方法进行解算,得到实验结果如图1～图4以及表3所示。

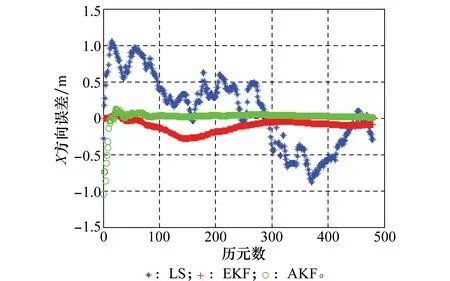
图1　3种解算方法X方向误差图Fig.1　X-component error of three methods

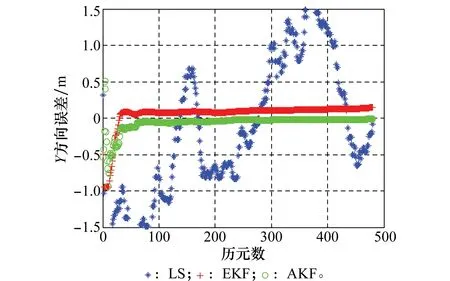
图2　3种解算方法Y方向误差图Fig.2　Y-component error of three methods

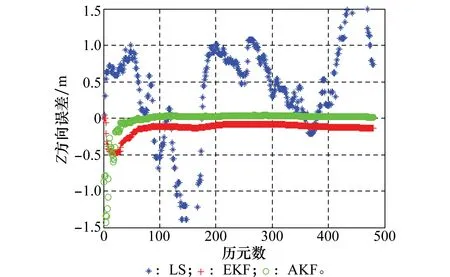
图3　3种解算方法Z方向误差图Fig.3　Z-component error of three methods

对比图1～图3中组合系统3种解算方法的位置误差曲线,可以看出,AEKF算法较之LS、EKF在定位精度及收敛速度方面有很大提升。LS方法由于没有将不同时刻的定位值联系起来相互制约,因而定位结果通常显得相当粗糙、杂乱,无法实现收敛;EKF方法由于初值及先验信息估计不够准确,导致收敛时间增加,收敛后的定位精度不够高;而AEKF方法由于通过LS方法得到了较为准确的滤波初值,滤波时间较短,定位结果较为理想。

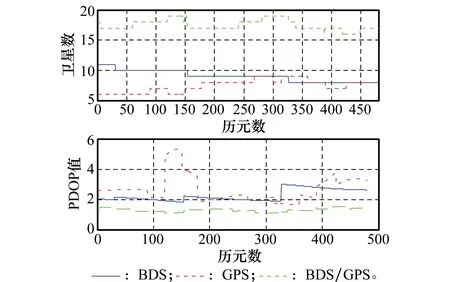
图4　3种定位方式卫星数及PDOP值Fig.4　Numbers of satellites and PDOP value of different systems

表3　BDS、GPS、BDS/GPS组合定位性能比较

对比图4及表3可以发现,虽然在大部分时间里BDS系统的卫星数要多于GPS系统,但是定位精度因子(positiondilutionofprecision,PDOP)有时没有GPS卫星的小,这主要是由于目前BDS系统的中地球轨道卫星较少,卫星空间结构不好造成的。目前BDS系统正处于全球组网阶段,其跟踪站数量有限,所提供的BDS卫星的精密轨道数据精度还不够高,而PPP解的优劣与卫星轨道和卫星钟差修正的精度有很大关系,并且,目前BDS系统只有14颗可用卫星,而GPS系统有32颗,其几何强度要远比BDS好。因此当前条件下BDSPPP的收敛时间明显长于GPSPPP[7]。而BDS/GPS组合系统相较单系统来说,极大提高了可用卫星的数目,从而改善了空间卫星几何分布。另外由图4可以看出,组合系统对PDOP值有平滑作用,使得数据处理收敛效果较好。这也是组合系统能够加快收敛时间的主要原因。定量分析发现,静态条件下,BDS系统PPP的X分量大部分优于5cm,Y分量大部分优于6cm,Z分量大部分优于5cm。GPS系统PPP的X分量大部分优于3cm,Y分量大部分优于3cm,Z分量大部分优于3cm。BDS/GPS组合系统PPP的X分量大部分优于1cm,Y分量大部分优于2cm,Z分量大部分优于2cm。

GPS系统X、Y、Z 3个方向上的均方根误差(rootmeansquare,RMS)统计均小于BDS系统,这是因为目前BDS卫星数较少,导致卫星几何构型和可靠性较差[14]以及精密轨道和精密钟差的精度相对较低。而BDS/GPS组合系统的卫星数目增加了约一半,卫星数目的增加使得相应的PDOP值有较大改善,定位精度可以得到明显提高。

2.2动态模式

为进一步验证算法在动态模式下的性能,在校园环境内开展动态试验。基准站和移动站均采用NovAtelPP6接收机,基准站与移动站之间的距离小于1km,整个动态实验时间约为22min,接收机运动速度较低(小于10m/s),数据采样率为1s,截止高度角为10°,图5为移动站运动轨迹图。在AEKF处理过程中,BDS和GPS载波相位观测量的观测噪声标准差均设为0.003m,伪距观测量的观测噪声标准差分别设为0.6m和0.3m。

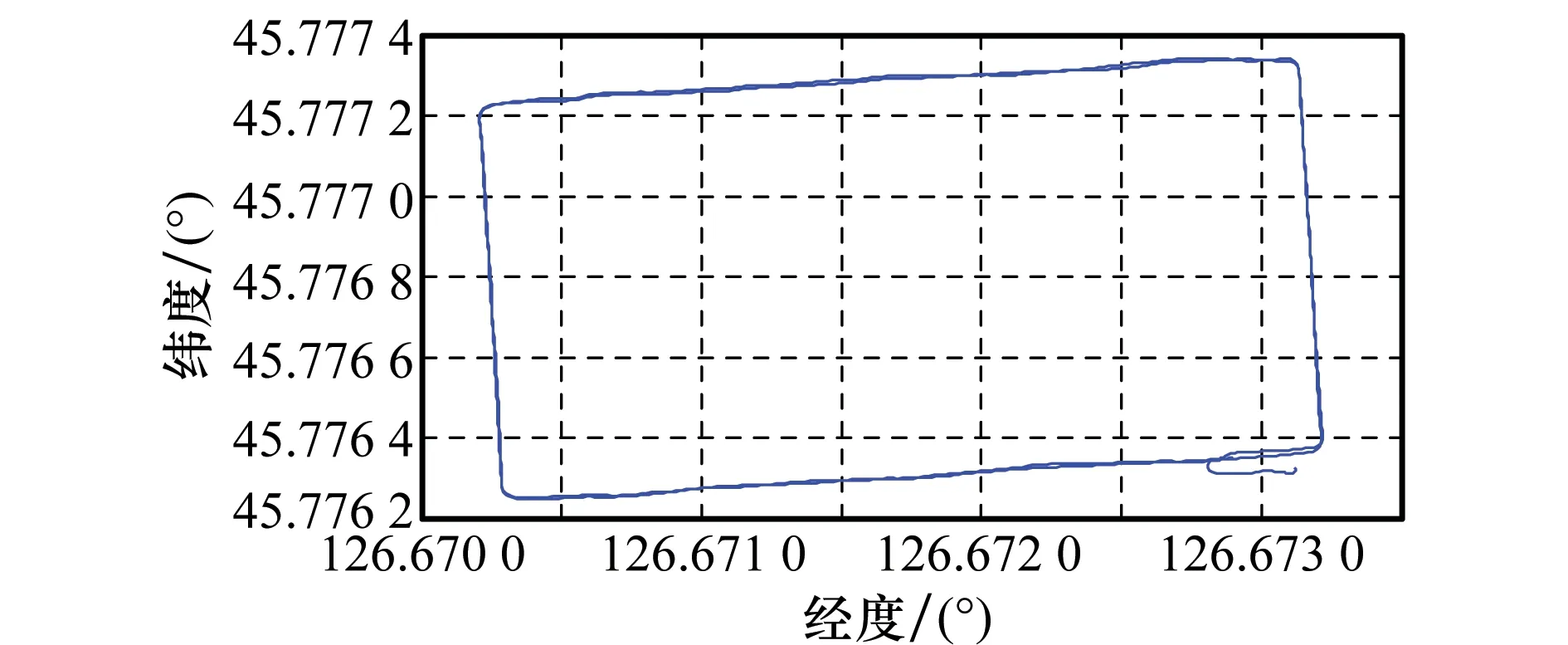
图5　移动站运动轨迹图Fig.5　Reference trajectory of rover user

为评估动态PPP精度,定位参考坐标来自于开源软件包RTKlib中的双频载波相位差分定位技术,定位精度可达到10cm级别。

运用LS、EKF、AEKF对BDS/GPS组合系统进行解算,以及运用AEKF对BDS单系统、GPS单系统、BDS/GPS组合系统进行分析,得解算结果如图6～图9及表4所示。

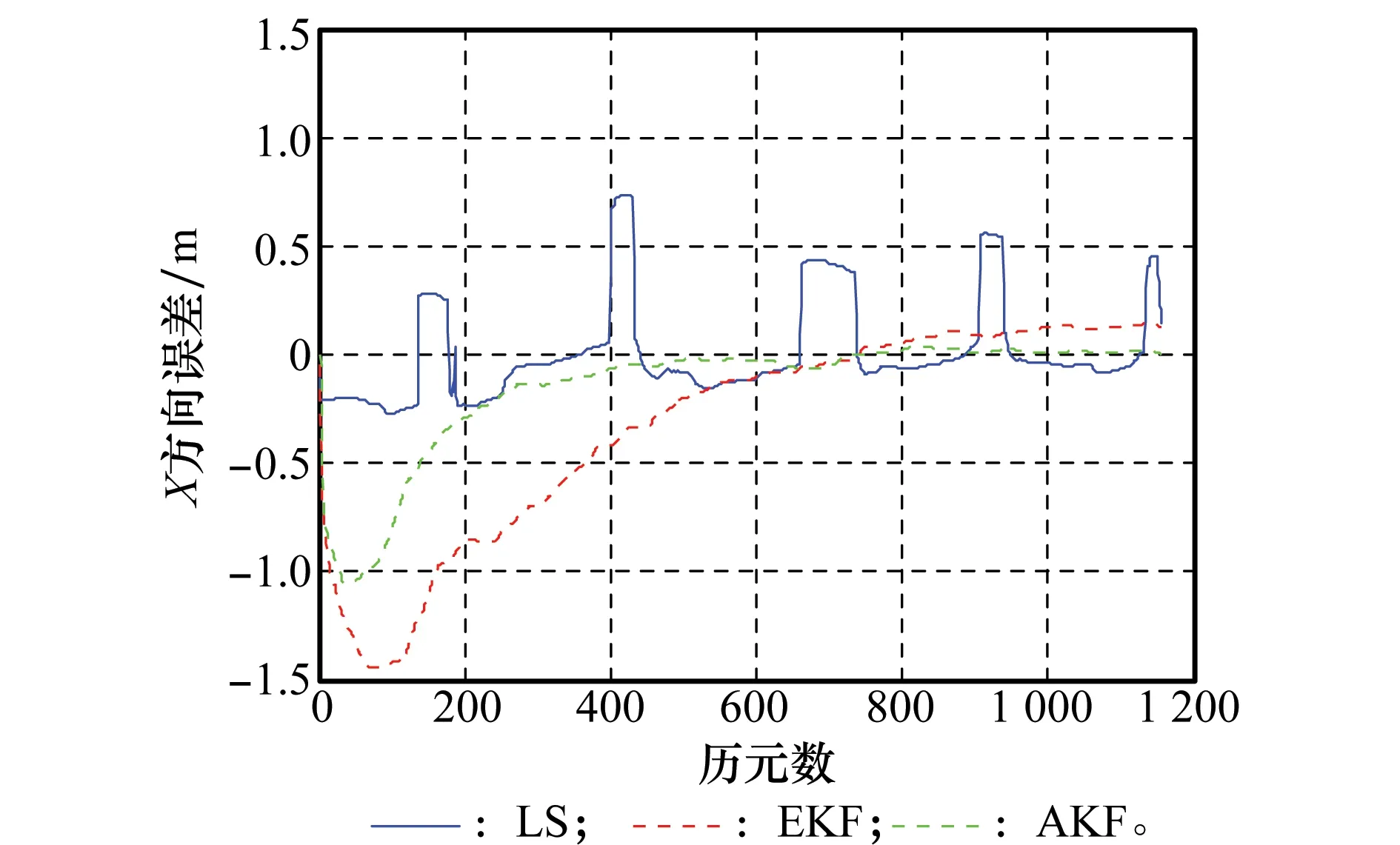
图6　3种解算方法X方向动态误差图Fig.6　X-component kinematic error of three methods

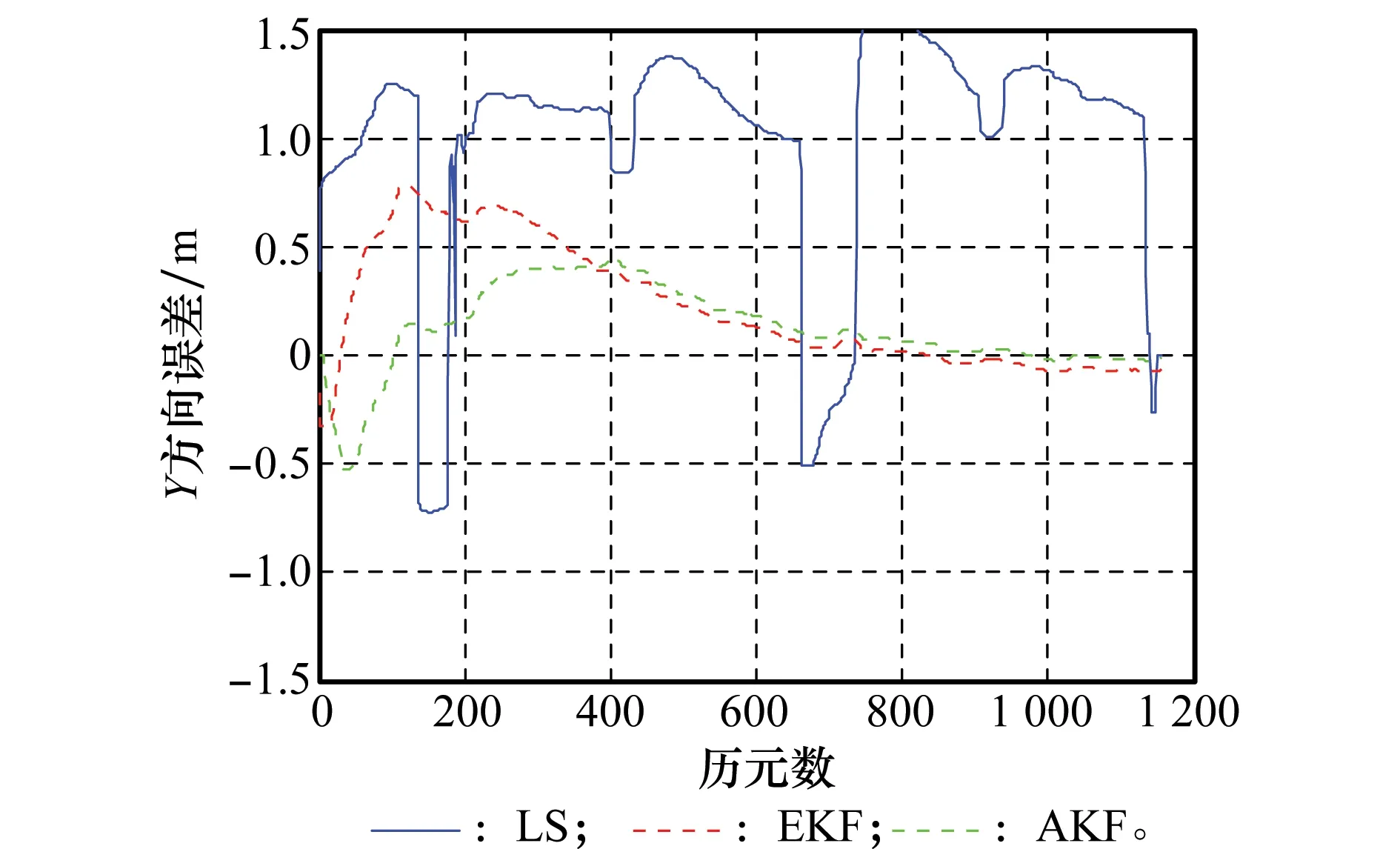
图7　3种解算方法Y方向动态误差图Fig.7　Y-component kinematic error of three methods

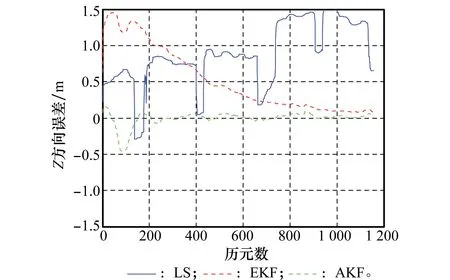
图8　3种解算方法Z方向动态误差图Fig.8　Z-component kinematic error of three methods

对比图6～图8中组合系统3种解算方法的位置误差曲线,可以看出,AEKF算法较之LS、EKF在定位误差及收敛速度方面有很大提升。与静态的情况相比,动态模式较为复杂,实际系统中,接收机的运动状态往往是未知的,同时运动的背景环境也可能是比较复杂的。因此在动态高采样率的情况下,LS方法由于忽略了各历元之间的关系,各历元定位结果之间存在突变情况,无法实现收敛,另外由图9中PDOP值的突变,解释了LS方法中定位误差的突变情况;同样地，在动态模式下,EKF对初值及先验信息的估计准确度更为敏感,由于先验信息估计不够准确,使得EKF估计方法收敛时间增加,收敛后的定位结果还不够好;AEKF的滤波初值及先验信息由最小二乘法得到,与通过经验值进行滤波初值设置的方法相比,本文所提AEKF算法的滤波性能相对更好,这在一定程度上弥补了运动的复杂性及高动态性,使得滤波时间相对较短,定位结果较为理想。

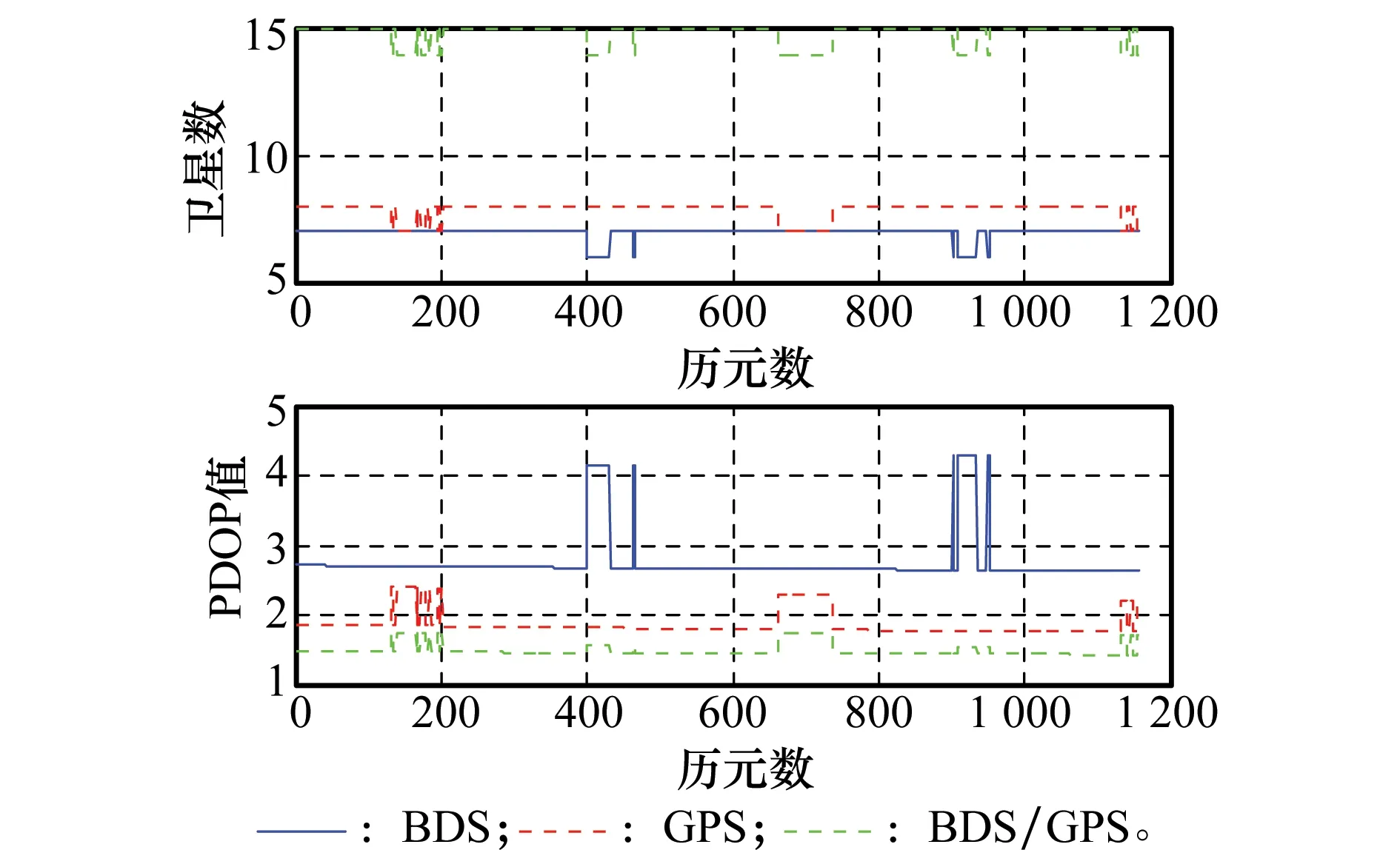
图9　3种动态定位方式卫星数及PDOP值Fig.9　Satellite number and PDOP in the kinematic mode

对比图9及表4可以发现,BDS系统的卫星个数要少于GPS系统,BDS对应PDOP值要明显大于GPS,然而随着BDS组网建设,将大大增加中轨道卫星的数目,因此BDS卫星的空间几何结构将会得到有效改善。此外,BDS测距精度和信号稳定性较GPS略差[15],相应地，在定位精度上BDS系统比GPS系统要差,而BDS/GPS组合系统由于卫星数量上的提高,使得系统的几何结构及定位可靠性增强,PDOP值相对单系统来说显著减小,使得定位精度有较大提高。

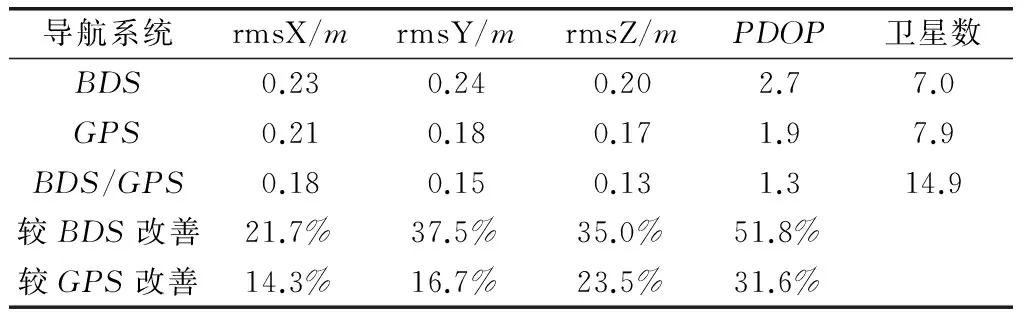
表4　BDS、GPS、BDS/GPS组合动态定位性能比较

从数值上看,组合系统对BDS系统PDOP值的改善效果要比GPS大得多,这主要是因为BDS尚不完善,卫星几何构型还不够好,因此导致其PDOP值较大。虽然目前BDS系统并不完善,在轨卫星较少,但是已经可以为GPS观测提供冗余观测量,对GPS几何构型的改善效果是显著的。单一的GPS或者BDS系统PDOP值在一些时刻变化较大,说明虽然该观测时段内系统的可用卫星数平均较多,但是由于卫星分布不均匀及信号失锁等原因,会造成单一系统定位结果不够准确,系统组合很好地解决了这个问题。为分析滤波收敛后的定位精度和稳定性,对结果进行分析,可以发现,动态条件下,收敛之后BDS系统PPP的X分量优于11cm,Y分量优于12cm,Z分量优于6cm。GPS系统PPP的X分量优于9cm,Y分量优于10cm,Z分量优于5cm。BDS/GPS组合系统精密单点定位的X分量优于4cm,Y分量优于6cm,Z分量优于4cm。

与静态模式相比,动态模式下,由于接收机的运动以及较高的采样率,使得对系统状态的估计更为困难,采用多系统组合相比单系统可以成倍地增加可视卫星数,卫星数目的增加使得相应的PDOP值有较大改善。另外,卫星数目的增加使得量测量增加,提高了量测冗余度。对比静态模式,可以看出,动态模式下,组合系统在性能上较之单系统幅度提高更大,效果更为明显。系统定位可靠性、连续性、精度都有了显著的改善。因此,多系统联合精密定位是可行的。

3　结　论

采用AEKF的方法,本文针对BDS/GPS组合PPP进行了改进研究与实现。一方面,与单系统PPP结果的对比分析发现,组合系统较单一系统在定位精度与收敛速度上都有显著提高,而且组合系统具有更多的可用卫星,能够保证定位的可靠性、可用性和连续性。另一方面,将AEKF应用于组合系统,相比传统方法,组合系统性能达到最优化,对动态的适应性有很大提高。

从实验结果来看,虽然单独BDS系统可以实现高精度定位,但是多个卫星导航系统联合定位,可以进一步提升精密定位的性能,本文的研究可为多个GNSS组合情况下的PPP提供一定的参考。

[1]ZumbergeJF.AutomatedGPSdataanalysisservice[J].GPS Solutions, 1999, 2(3): 76-78.

[2]ZhangXH,LiuJN,ForsbergR.Applicationofprecisepointpositioninginairbornesurvey[J].Geomatics and Information Science of Wuhan University, 2006, 31(1): 19-22.

[3]LiX,GeM,ZhangH,etal.TheGFZreal-timeGNSSprecisepositioningservicesystemanditsadaptionforCOMPASS[J].Advances in Space Research, 2013, 51(6): 1008-1018.

[4]HeF,GaoCF,PanSG.ApplicationofrobustHelmertvariancecomponentestimationinGPS/BDS/GLONASSintegratedpositioning[J].Journal of Navigation and Positioning, 2013, 1(3): 56-61.

[5]ZhaoL,LiL,SunM,etal.NoveladaptivehatchfiltertomitigatetheeffectsofionosphereandmultipathonLAAS[J].Journal of Systems Engineering and Electronics, 2010, 21(6): 1046-1053.

[6]ZhaoL,WangXX,LiL,etal. Nonlinear system filtering theory[M].Beijing:NationalDefenseIndustrialPress,2012.(赵琳,王小旭,李亮,等.非线性系统滤波理论[M].北京:国防工业出版社,2012.)

[7]ZhangXH,ZuoX,LiP.ConvergencetimeandpositioningaccuracycomparisonbetweenBDSandGPSprecisepointpositioning[J].Acta Geodaetica et Cartographica, 2015, 44(3): 250-256.

[8]MengXG,GuoJM.ResearchonGPS/GLONASSintegratedprecisepointpositioning[J].Geomatics and Information Science of Wuhan University, 2010, 35(12): 1409-1413.

[9]LiL.Groundbasedaugmentationsystempositioningandintegritymonitoring[D].Harbin:HarbinEngineeringUniversity,2012. (李亮. 陆基增强系统定位与完好性监测技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.)

[10]SouzaMFD,LuoZQ.Finite-horizonrobustKalmanfilterdesign[J].IEEE Trans. on Signal Processing, 2001, 49(9): 2103-2112.

[11]ZhangSX. Technology and application of GPS[M].Beijing:NationalDefenseIndustrialPress, 2004. (张守信.GPS技术与应用[M]. 北京: 国防工业出版社, 2004.)

[12]YeSR.TheoryanditsGPSprecisepointpositioningusingun-differencedphaseobservation[D].Wuhan:WuhanUniversity, 2002.(叶世榕.GPS非差精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002.)

[13]YueXK,YuanJP.AnadaptiveKalmanfilteringalgorithmbasedonmaximum-likelihoodcriterion[J].Journal of Northwestem Polytechnical University, 2005, 23(4): 469-474.

[14]JinB,YangSW,LiuWK.AnalysisofGPS/BDSintegratedsinglepointpositioning[J].Hydrographic Surveying and Charting, 2013, 33(4): 39-41, 65.

[15]TangWM,XuK,JinL,etal.TestandanalysisofBeidou/GPScombinedpseudorangepointpositioningperformance[J].Geomatics and Information Science of Wuhan University, 2015, 40(4): 529-533. (唐卫明, 徐坤, 金蕾, 等. 北斗/GPS组合伪距单点定位性能测试和分析[J].武汉大学学报(信息科学版), 2015, 40(4): 529-533.)

李亮(1984-),通信作者,男,讲师,博士,主要研究方向为卫星导航定位与完好性监测。

E-mail:liliang@hrbeu.edu.cn

王雪(1992-),女,硕士研究生,主要研究方向为精密单点定位。

E-mail:wangxue_407@hrbeu.edu.cn

BDS/GPS integrated precise point positioning based on adaptive extended Kalman filter

ZHAO Lin, ZHANG Sheng-zong, LI Liang, WANG Xue

(CollegeofAutomation,HarbinEngineeringUniversity,Harbin150001,China)

In order to achieve the shorter convergence period and better positioning accuracy for precise point positioning (PPP), the combination of multiple navigation satellite, such as the Beidou navigation satellite system (BDS) and the global positioning system (GPS), and the better positioning method are two ways to choose. However, since the traditional least square (LS) estimator ignores the temporal correlation of observations, and the extended Kalman filter (EKF) is limited by inaccurate prior information, a novel PPP method based on adaptive extended Kalman filter (AEKF) is used to adjust the process noise with the measurement consistency test. The experiment results show that, compared with traditional EKF solution, the convergence period of PPP based on AEKF can be shorten by 9 minutes, and the accuracy of positioning can be increased by 33.7%.

precise point positioning (PPP); convergence period; positioning accuracy; adaptive extended Kalman filter (AEKF)

2015-10-14；

2015-12-21；网络优先出版日期：2016-02-18。

国家自然科学基金(61304235，61273081, 61304234)；中央高校基本科研业务费(HEUCF160416)；黑龙江省博士后科研启动基金(LBH-Q15033, LBH-Q14054) 资助课题

U 666.1

A

10.3969/j.issn.1001-506X.2016.09.25

赵琳(1968-),男,教授,博士,主要研究方向为卫星导航、惯性导航。

E-mail:zhaolin@hrbeu.edu.cn

张胜宗(1988-),男,硕士,主要研究方向为卫星导航、精密单点定位。

E-mail:zhangshengzong@hrbeu.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160218.1209.004.html