郭守敬圭表测影推算冬至时刻的模拟测量研究

肖 尧 孙小淳

(中国科学院大学 人文学院,北京 100049)

郭守敬圭表测影推算冬至时刻的模拟测量研究

肖 尧 孙小淳

(中国科学院大学 人文学院,北京 100049)

元朝郭守敬首创用四丈高表和景符进行测影,以推算冬至时刻,所得到的冬至时刻具有很高的精度。本文通过模拟测量的方法,对郭守敬圭表测影定冬至时刻的方法及其精度进行探究。利用北京古观象台的圭表进行模拟测量,并以古法推定了2014年的冬至时刻,与郭守敬在至元年间(1277—1280)的测定相比较。对郭守敬测定的冬至时刻与模拟测量推算的冬至时刻进行分析,探讨郭守敬所推得的冬至时刻精准的原因以及“授时历议”中所载测影数据的取舍问题。

圭表测影 郭守敬 授时历 模拟测量 冬至时刻

在中国古代历法中,节气时刻的测定是十分重要的工作,而在所有节气中,又以冬至时刻的测定最为重要,因为历法推算以冬至为起算点。元朝郭守敬制订《授时历》,其中推定的冬至时刻相比于过去的历法,在精度上有很大的提高[1]。《授时历》中的冬至时刻是郭守敬使用圭表测影数据,通过一套方法推算确定的。之前有关郭守敬确定冬至时刻的研究多以郭守敬圭表测影的精度为重点,所依据的数据大多直接采用《元史·历志》所载数据[1—5]。然而仅仅说明测量精度的高低尚不足以对郭守敬测定冬至时刻的过程有全面的了解。郭守敬获得精度较高的数据取决于哪些因素？郭守敬在数据使用上又有何取舍？这些问题,有必要进一步探讨。

本文通过模拟测量对郭守敬圭表测影定冬至时刻的方法进行研究。使用北京古观象的“八尺”表测量2014年冬至前后若干天的正午影长,然后使用这些影长数据,以郭守敬所使用的推算方法推定2014年的冬至时刻。通过对模拟测量的精度与郭守敬在元朝至元年间测量的精度的比较,探讨郭守敬圭表测影方法的合理性以及他如何处理数据和误差。

1 圭表测影的模拟测量

《元史·历志》“授时历议”中记载的推算冬至时刻,其平均误差在2刻左右,这在当时而言十分精确[3,6]。郭守敬测定冬至时刻可分为两个环节,一是圭表测影,二是使用测影数据推算冬至时刻。圭表测影是前期的基础工作,测影准确与否直接影响到后面的推算精度。郭守敬在测影工作中不仅改进和新制仪器[7—9],而且改良了测影方法([10],996页),以此来提高测影精度。

根据《元史·天文志》中的记载,郭守敬对圭表测影工作的改进可以归为三处：一是改八尺表为四丈高表([10],996页),使影长变化更加明显,便于观察,同时在影长读数精度不变的情况下提高了测量相对精度；二是变过去的测日体上边影为测日体中心影,更为准确。《元史·天文志》载：“旧法一表端测晷,所得者日体上边之景。今以横梁取之,实得中景,不容有毫末之差”([10],997页)；三是创制景符([10],997页)通过小孔成像使虚影区同比例缩小,解决虚影读数误差过大的问题,提高影长读数的精度。为了更好地认识郭守敬圭表测影的过程和效果,我们采用模拟测量的方法探究郭守敬的圭表测影工作。

1.1 使用八尺表进行的模拟实测

郭守敬测影使用了四丈高表和景符([11],320页)。由于条件所限,模拟观测使用的是北京古观象台八尺铜圭表*此圭表石座为明代实物,其上铜表为1983年在明代石座上复原的元郭守敬八尺铜表。和北京古观象台复原的景符([12],134页)。其中,八尺铜表顶端由两龙爪擎一横梁(梁直径0.06景表尺,1景表尺=24.525厘米[13]),梁心距圭面垂直距离应为8景表尺,我们实测为7.995景表尺,下面的计算都以后者为准。横梁垂直投影与圭表刻度零位线重合,所以横梁在圭面上投影位置即为影长。图1和图2分别为复原的“八尺”铜表和景符。我们在北京古观象台测量了2014年冬至前后约半个月每天正午的影长数据。

图1 北京古观象台八尺圭表

图2 北京古观象台复原景符

测影工作从2014年12月5日开始,到2015年1月7日结束。每日在北京观象台地方时正午时刻测量表影长度。通过观察表影在圭面上的位置判断何时为古观象台正午时刻,当表影与圭面南北边平行时,即为古观象台正午。由于太阳真时与太阳平时的差值每日稍有不同,观象台每日正午对应的北京时间都不相同,同时我们的每次测量需要用时10秒左右(这个时间内表影长度的变化可忽略),可能造成记录的观象台正午时刻有一些误差。测量时将景符正放于圭面的南北中轴线上,正午时会看到太阳光透过景符小孔在圭面上成米粒大小的光斑(太阳倒像),这时在圭面南北中轴线上移动景符,使横梁影出现在光斑中,当横梁影平分光斑时,读横梁影的上下沿所在刻度。实测中使用读横梁上下沿影长的方法,原因是实测中光斑内的横梁影的中心位置不易读准,只能凭感觉判断。相比之下,读上下沿影长数值更加准确,读数时的虚影影响更小,仅0.2毫米左右的误差(见图3、图4)。

图3 表端横梁通过景符形成的影像

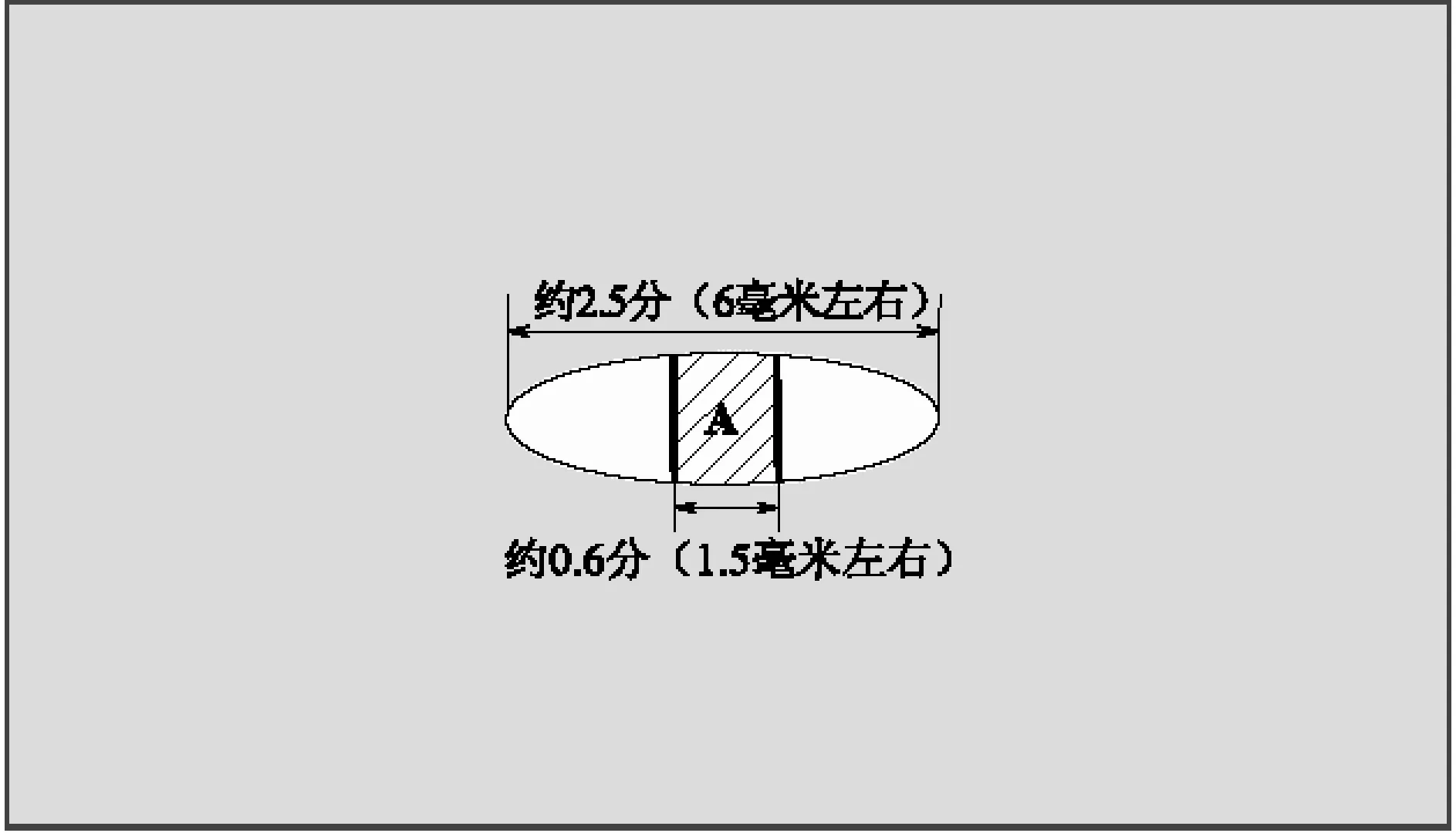
图4 使用景符读取影长示意图,A区域为横梁阴影

从2014年12月5日起,除12月9日天阴未有观测数据,共测得33组观测数据列于表1。

表1 使用北京古观象台八尺表测影数据表

续表1

在北京古观象台测量之后,我们又前往登封告成的古观象台,利用四丈高表进行了初步的测量。发现在使用景符的情况下,八尺圭表和四丈高表的测量效果相差不大,即两者在影长测量精度上是相当的,因此使用八尺表所做的模拟实测,大致上可以反映出四丈高表的测量水平。同时,登封告成四丈高表的测量工作由当地的曹书敏跟进,待有更完整的数据时可以做进一步的研究。

1.2 模拟实测影长的精度

将实测影长数据与理论推算影长数据进行比较,就可分析实测影长的精度。崔石竹、李东生曾做过类似的研究([14],332—341页),但最后结果与我们所得的有所不同。利用《2014年中国天文年历》所载的每日力学时0h的视赤纬和大气蒙气差,用贝塞尔内插法(北京古观象台圭表处地理经度λ东经116°26′2.8″,地理纬度φ北纬39°54′19.3″,海拔40米)求出某日日中天(日中天时间为我们实测的地方正午时,换算为力学时)的太阳视赤纬δ,利用公式

α=90°-φ+δ

求出太阳中天时地平高度α,再加蒙气正R0,得太阳实际地平高度为α1=α+R0。圭表高为7.995尺,于是影长的理论值为

S=7.995×cotα1

现将33组数据的理论影长值计算结果与实测影长结果列于表2进行分析(理论影长数据使用的大气蒙气差均为未修正大气蒙气差)。

表2 北京古观象台八尺表测影数据与理论值比较表

在实测的33天中,有4天的光强很弱(在表2中用加粗标记),辨别横梁影的位置已相当困难,偶然误差增大,故在数据分析中剔除这4组数据,只分析剩余的29组。实测地方正午时与理论地方正午时相差30秒左右,这应该是判别表影正北位置时的人为误差,但只要在正午时前后1分钟以内,太阳高度角变化和太阳视赤经变化对影长的影响都可忽略不计*在正午时刻前后1分钟以内,太阳高度角变化小于2″,太阳视赤经变化小于2.5′,这两者引起的影长变化小于0.01毫米,因此对测量而言可以忽略。。

对29组数据进行分析得到：29组数据的理论影长值与测量影长值之差(理论影长值-测量影长值),正值9个,负值20个,由于数据样本不大,因此不好作为判别是否存在某种系统误差的依据。29组数据的理论影长值与测量影长值差值的平均值为-0.0012景表尺(约-0.3毫米),绝对值最大的差值为2014年12月22日的-0.0082景表尺(约2毫米),29组理论影长值与测量影长值差值的标准差为0.0043景表尺(约1.1毫米)。表明理论影长值与测量影长值的平均偏离程度为0.0043景表尺,相对误差水平约为0.03%。考虑到样本数据较少,以最大误差值做估计,冬至前后的影长实测误差在0.0082景表尺左右,即误差水平在2毫米左右,相对误差水平在0.05%左右。

2 以圭表测影数据定冬至时刻

在中国古代,圭表测影很早就被用作判断节气的方法([15],363页)。在刘宋祖冲之之前,古人尚不能通过圭表测影得到准确的冬至点时刻[1]。用圭表测影的影长数据来推算冬至点时刻,始于刘宋祖冲之([16],313页)。《元史·历志》“授时历议”中就有“纪元以后诸历,为法加详,大抵不出冲之之法”([10],1122页)的说法。这套方法假设的前提是：在冬至点前后,影长随时间的变化是对称的,即：当冬至前后两个时刻距冬至时刻相等时间,这两个时刻的表影长度相等。这样,祖冲之的这套方法实质上就是寻找冬至前后影长相等的两个时刻,之后确定这两个时刻的中间点时刻,定其为冬至时刻。下面用数学化的方式进行说明,设A为冬至前某日,B和C(=B+1)为冬至后相邻两日；F为冬至后某日,D和E(=D+1)为冬至前相邻两日。a、b、c、d、e,f分别表示相应日正午的影长值。O点为冬至时刻,相距O点相等时间的A与A’,F与F’的影长相等,O点时刻即为A与A’,F与F’时刻的中点时刻。具体有6种情况,如图5所示,图中O点为冬至时刻点,OA=OA’,OF=OF’,a’=a,f’=f。

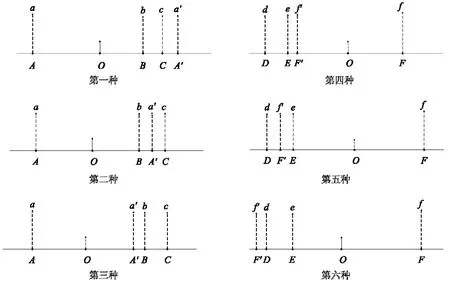
图5 郭守敬推算冬至时刻算法的6种情形示意图

陈美东将这套推算至日方法归为以下两式([2],301页)：

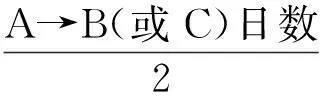
李勇最近对上述方法进行过全面的解读,指出了这套确定节气时刻方法的近似性质[3]。本文则从这套推算方法本身精度的角度进行分析。

2.1 按郭守敬推算方法根据模拟测量数据求得的2014年冬至时刻

在实测的29组数据中,冬至日前后1—2天内的影长数据未使用,原因是冬至日前后1—2天内的影长数据变化很小,与观测的误差接近,使用这部分影长数据进行除法运算会使结果出现显著偏差(故12月20日至12月23日这4天的数据未使用)。现将选取日期组合和推算冬至时刻列于表3(所有结果都为12月22日X刻,故日期不列)。

表3 推算冬至时刻选取日期组合与推算冬至时刻表

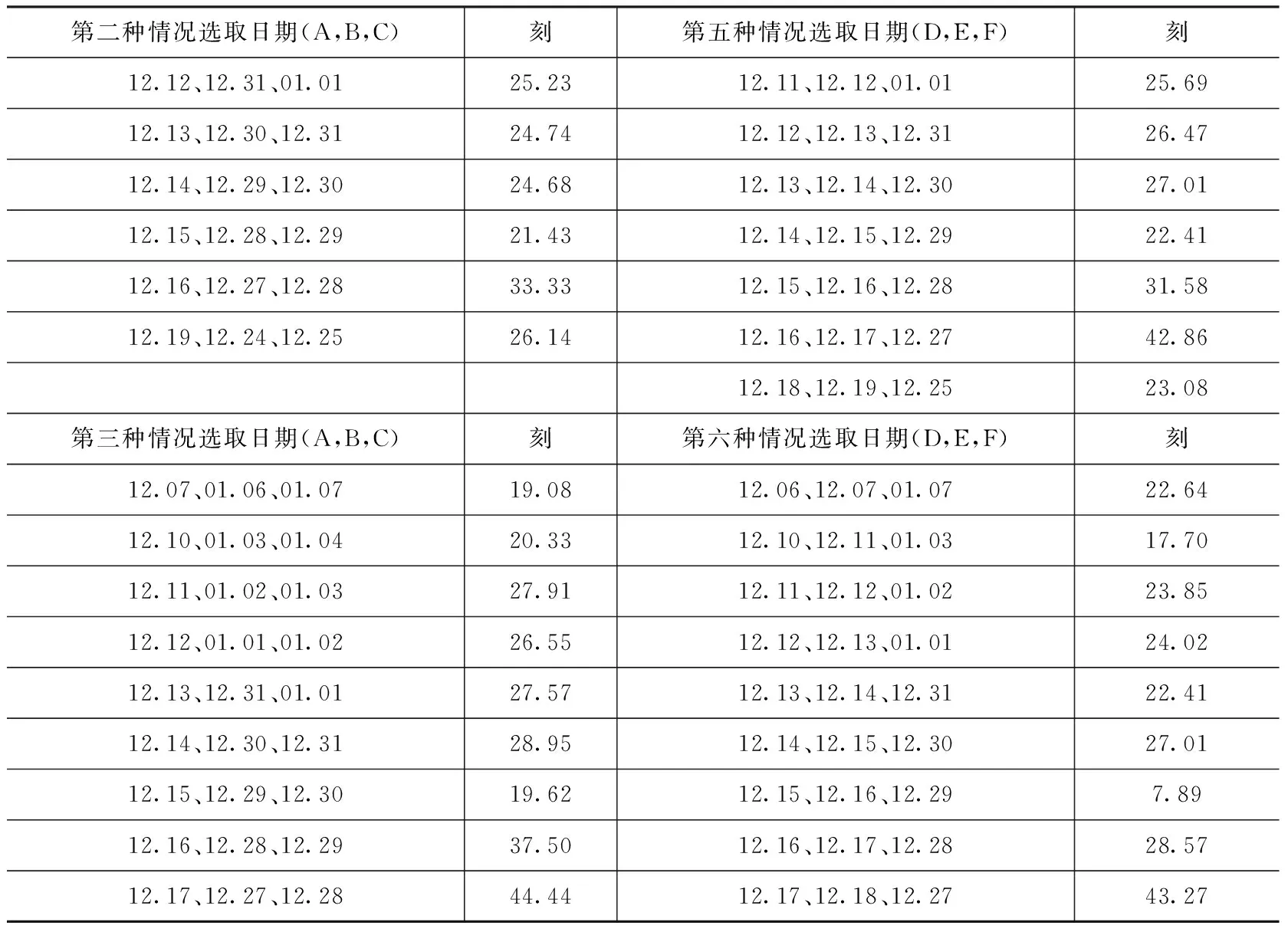
续表3

以取平均值的方式定冬至时刻,6种情况分别得到6个平均值：26.16刻、24.82刻、27.99刻、27.09刻、26.90刻、24.15刻。根据《2014年中国天文年历》,2014年的冬至时刻为北京时间12月22日7时3分1秒,换算成北京古观象台地方平时为12月22日6时48分45秒,即12月22日28.40刻。6个平均值与其最大的差值为第六种情况的4.25刻(61.2分钟),最小的差值为第三种情况的0.41刻(约5.9分钟),6个平均值的均值为26.185刻,与真冬至时刻相差2.215刻(约31.9分钟)。

通过实测影长推算的冬至时刻表明：使用郭守敬推算冬至时刻的方法,利用2014年冬至前后半个月的影长数据得到的冬至时刻平均误差在2刻左右。这个结果同郭守敬时误差相当,说明郭守敬推算冬至时刻的方法在如今取前后半个月测影数据的范围内,依旧可以得到不错精度的冬至时刻。

2.2 郭守敬以圭表测影数据推算冬至时刻方法的合理性分析

郭守敬使用的冬至时刻推算的方法中,影响最终结果的因素主要有两个,一是圭表测影的精度,二是推算方法的精度。圭表测影的精度已经通过模拟测量进行了探析,下面对冬至时刻推算方法的精度进行分析。

郭守敬的这套冬至时刻推算方法若要行之有效,需要满足三个条件。第一个条件是一日内的影长线性变化；第二个条件是相邻两日的影长变化量相等；第三个条件是影长在冬至点前后对称变化。这其中,6种情况的推算方法都必须满足第一个和第三个条件,且第一种、第三种、第四种和第六种情况的推算方法还需要满足第二个条件。下面就对这三个条件进行分析。

第一个条件为一日内的影长线性变化。以现今知识来看,一日内的影长并不线性变化,影长等价于太阳地平高度角的余切值,就一日内的影长变化而言,其变化与线性变化十分接近,所以此条件与实际情况基本符合。

第二个条件为相邻两日的影长变化量相等。以现今知识来看,相邻两日的影长变化量并不相等,以八尺表为例,冬至前后15天范围内相邻两日的影长变化量差值在1毫米左右,当一日的影长变化量远大于1毫米时,第二个条件引起的误差可忽略。

第三个条件为影长在冬至点前后对称变化。可以理解为距冬至点相等时间的两个时刻影长相等。以现代天文学知识来看,当冬至点与近日点位置一致时,可近似认为冬至点前后的影长对称变化。因为近日点前后的地球公转速率可近似认为对称变化,这使得距近日点相等时间的两个时刻的太阳高度角大致相等,因此影长大致相等。通过《中国天文年历》得到2013年、2014年和2015年冬至点与地球近日点分别相差14°3′、13°32′和11°59′(误差在2′以内)；再利用Skymap Pro 11.0软件回推得到1278年、1279年和1280年冬至点与地球近日点分别相差9′、1°26′和-30′(误差在5′以内)。可以看出,在郭守敬年代,冬至点与近日点更加靠近,则此条件与实际情况更加符合,所以郭守敬时期这套方法推算冬至时刻更为准确。有关此点我们可以通过使用理论影长值,按郭守敬法推得的冬至时刻的误差变化加以说明。图6和图7分别表示1279年和2014年的情况。影长数据都采用冬至前后3—60天的理论影长值。图中标有“一”“二”“三”“四”“五”和“六”的曲线,分别表示上述郭守敬使用的6种推算情况推得的冬至时刻误差随所取影长所在日距冬至时刻的日数的变化趋势。

图6 1279年取表影日期距冬至日天数与推算方法精度关系

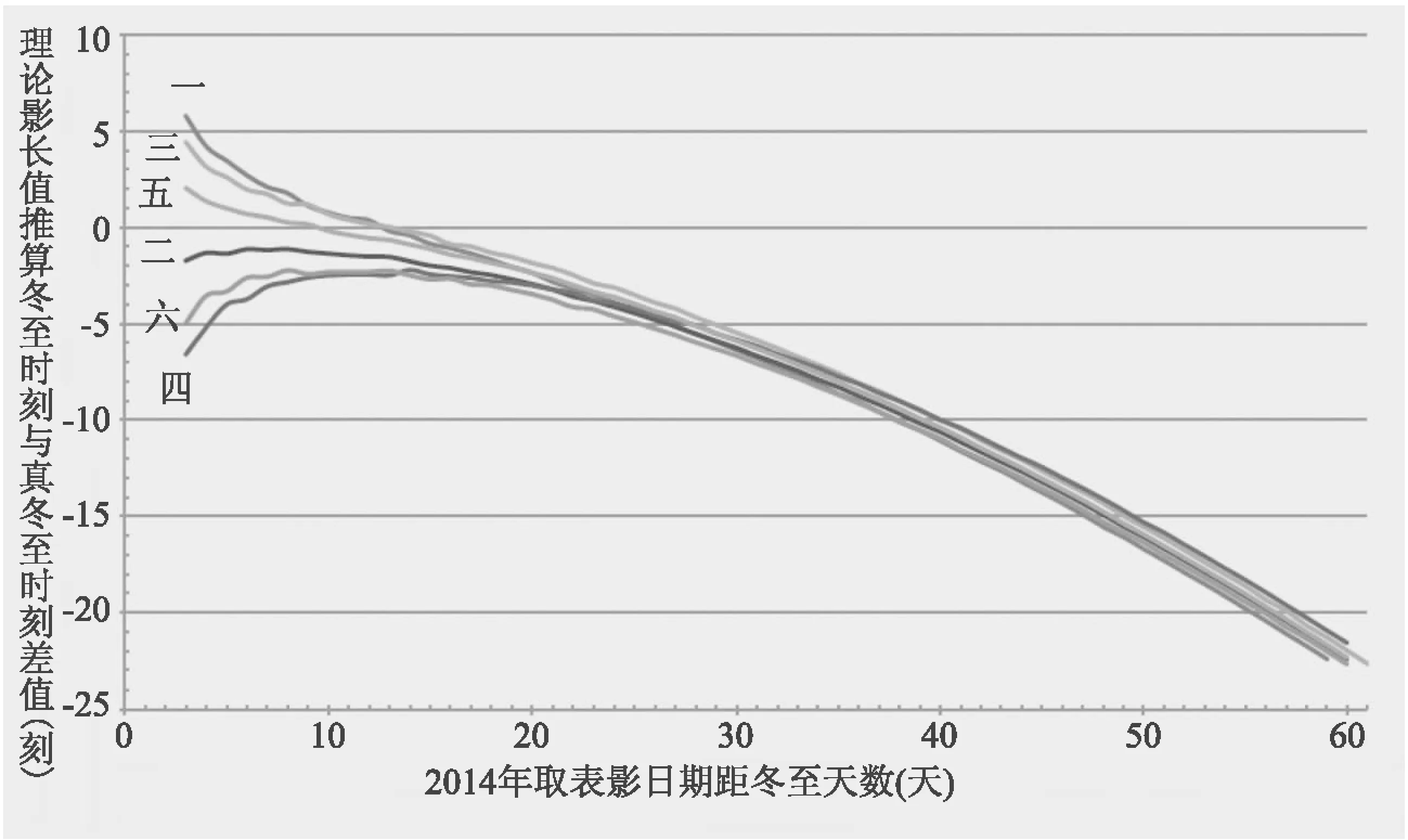
图7 2014年取表影日期距冬至日天数与推算方法精度关系

从图6看1279年的情况,当所取表影日期距冬至前后为15天以内时,按理论影长推算得到冬至时刻的误差整体上随天数增加而减小,到15天以外,误差基本固定在1刻左右。这表明,这套冬至推算方法在1279年时取表影日期距冬至天数在15天以上时有很好的准确度。从图7看2014年的情况,误差最小的部分在取表影日期距冬至前后11天左右,其误差在3刻左右,随着取表影日期距冬至天数的增加,其误差逐渐增大,在取表影日期距冬至60天左右时,误差已经达到20刻(288分钟)以上。这表明这套冬至推算方法在2014年时随着取表影日期距冬至天数(11天以上)的增加误差将越来越大。

基于以上分析,我们认为《元史·历志》“授时历议”中所载的高精度冬至时刻不仅得益于郭守敬准确的圭表测影数据,而且得益于当时冬至点与地球近日点比较接近,冬至点前后影长变化比较对称的实际情况,使得他使用的方法可以比较好地适用。以《元史·历志》“授时历议”中的取表影日期来看,其中有不少取表影日期距冬至30天以上的日期组合,但推算结果误差也不大。如果换成2014年,误差就会很大。因此我们在2014年做模拟测量时,只测量了冬至15天以内的影长,而15天以外的数据,因为推算方法本身就产生了很大误差,再对其分析相对就失去了意义。

2.3 《授时历》中选取哪些测影数据推算冬至时刻？

在《元史·历志》“授时历议”中共有3年的推算冬至时刻的53条测影数据。现将《元史·历志》“授时历议”中的冬至推算选取日期组合,及其所用推算情况和推算结果列于表4(“授时历议”中原文虽未明指使用了哪种推算情况,但根据其所选日期组合即可判断其所用推算情况)。

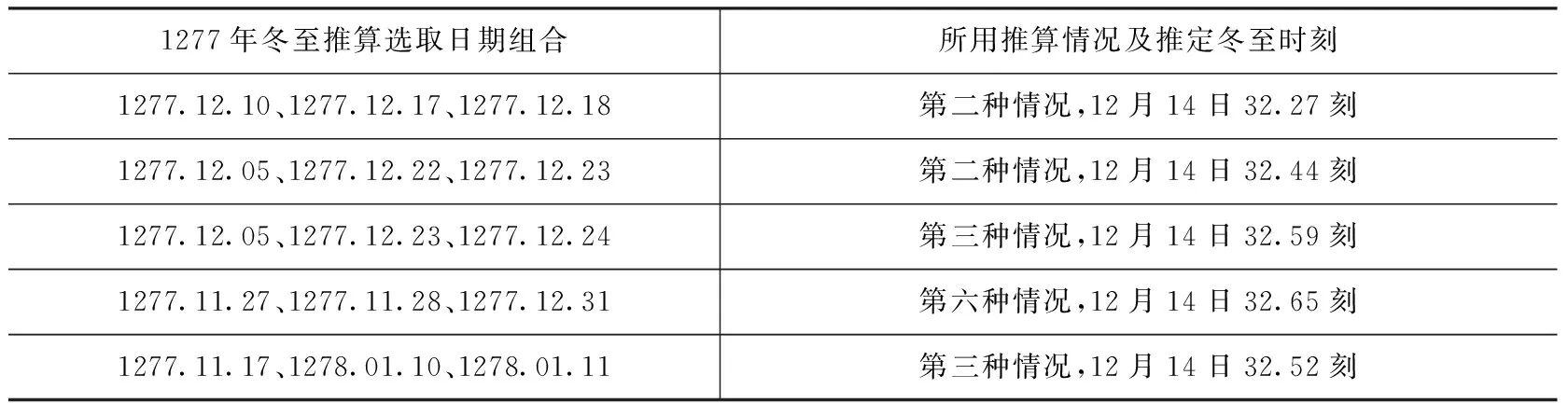
表4 1277—1279年冬至推算日期组合及冬至时刻表

续表4

表4中1278年1278.06.19、1279.06.09、1279.06.10三天的数据使用第一种推算方法得到的结果为51.88刻(表中用加粗标记),与所记载的1278年冬至时刻58刻明显不合,推测为1278.06.19的数据“五月二十八日庚戌,景一丈一尺七寸八分”([10],1126页)抄录错误,若改为一丈一尺七寸七分,最后的结果为58.13刻,则较为合理。

需要指出,“授时历议”给出的上述数据组合并不是所有可能的组合,而是经过筛选的。试看“授时历议”中关于推算1278年(至元十五年戊寅岁)冬至时刻和推算1279年(至元十六年己卯岁)冬至时刻的两段记载：

推十五年戊寅岁冬至

十一月十二日辛卯,景七丈五尺八寸八分一厘五毫；十三日壬辰,景七丈六尺三寸一厘五毫；闰十一月十五日甲子,景七丈六尺三寸六分六厘五毫；十六日乙丑,景七丈五尺九寸五分三厘；十七日丙寅,景七丈五尺五寸四厘五毫。用壬辰、甲子景相减为实,以辛卯、壬辰景相减为法,除之,亦得戊申日未初三刻。或用甲子、乙丑景相减,推之,亦合。若用辛卯、乙丑景相减为实,用乙丑、丙寅景相减,除之,并同。此取至前后十六七日景。([10],1125页)

推十六年己卯岁冬至

十月十八日壬辰,景七丈四尺五分二厘五毫；十九日癸巳,景七丈四尺五寸四分五厘；二十日甲午,景七丈五尺二分五厘；至十一月二十八日壬申,景七丈五尺三寸二分；二十九日癸酉,景七丈四尺八寸五分二厘五毫；十二月甲戌朔,景七丈四尺三寸六分五厘；初二日乙亥,景七丈三尺八寸七分一厘五毫。用甲午、癸酉景相减,癸巳、甲午景相减,如前推之,亦同。若以壬申、癸酉景相减为法,推之亦同。此取至前后十八九日景。若用癸巳与甲戌景相减,以壬辰、癸巳景相减,推之,或癸巳、甲午景相减,推之,或用甲戌、癸酉景相减,推之,或甲戌、乙亥景相减,推之,或以壬辰、乙亥景相减,用壬辰、癸巳景相减,推之并同。此取至前后二十日景。([10],1128—1129页)

其中推1278年(至元十五年戊寅岁)冬至的这一段给出了5天的测影数据,分别是1278年11月27日,1278年11月28日,1278年12月30日,1278年12月31日和1279年1月1日,这5天的数据可以有7种推算组合,而“授时历议”中只给出了3种推算组合,另外4种推算组合没有给出；推1279年(至元十六年己卯岁)冬至的这一段给出了7天的测影数据,分别是1279年11月23日,1279年11月24日,1279年11月25日,1280年1月2日,1280年1月3日,1280年1月4日和1280年1月5日,这7天的数据可以有13种推算组合,而“授时历议”中只给出了7种推算组合,另外6种推算组合没有给出。将上述日期组合、推算情况和结果,与“授时历议”所载冬至时刻误差列于表5。

表5 《授时历》推算冬至时刻所载日期组合和未载日期组合表

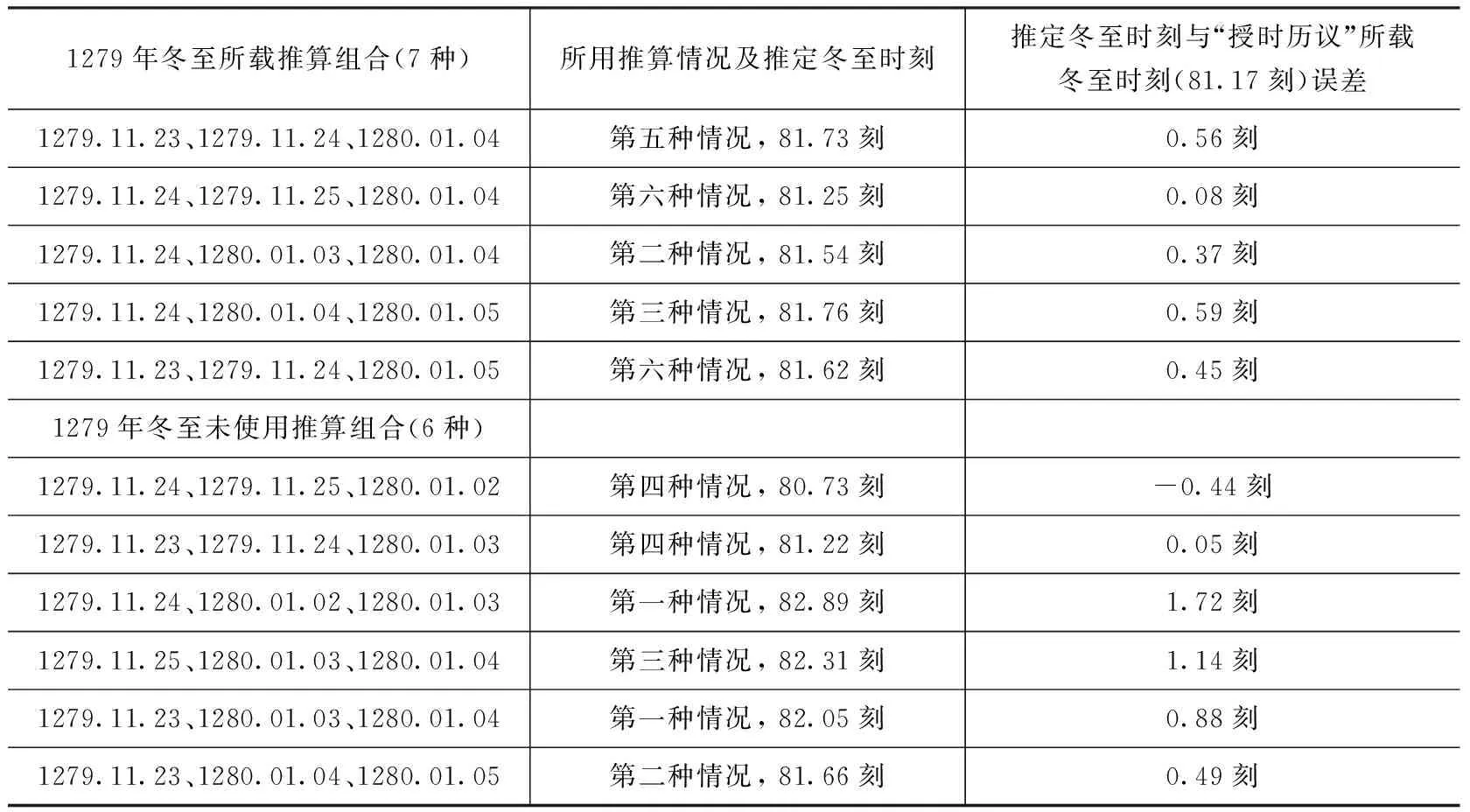
续表4

从表5发现,“授时历议”中所选取的10种推算影长组合的计算结果都在最后所载的冬至时刻后一刻以内,而未使用的10种推算影长组合中仅有3种计算结果在所载的冬至时刻后一刻以内,另外7种推算影长组合的结果皆不在冬至时刻后一刻以内。我们发现,《元史·历志》“授时历议”中所载的日期组合得到的冬至时刻都在所载冬至时刻后一刻以内,这说明郭守敬使用“后一刻以内”的标准来判断推算的冬至时刻是否“正确”,进而筛选出“正确”的数据组合。

3 结 语

通过对郭守敬圭表测影方法的模拟测量,表明八尺表与景符的配合使用已经能达到很高的测影精度。使用八尺表和景符的情况下其测影精度已达2毫米左右,相对误差水平在0.05%左右。

郭守敬以圭表测影数据推算冬至时刻的方法,在计算上可以直接得到冬至日和冬至时刻,并且将选取的影长数据类型拓展为6种。本文通过数据分析和图表展示表明：整体上,6种推算情况中的第二种和第五种推算情况推得的冬至时刻与真冬至时刻的接近程度最好,其原因是第二种和第五种推算情况要求的假设条件比其他四种推算情况少一条。同时,我们利用模拟观测的29组数据推算2014年冬至时刻平均误差为2.215刻,而郭守敬时期实测推算冬至时刻与真冬至时刻平均误差水平在2.5刻以内。需要注意的是,“授时历议”所载的冬至测影数据选取的日期距冬至日数有多有少,最多达178天,若以同样的选取方式进行日期选择用以推算2014年冬至时刻,则误差将远大于2.5刻,这是由于2014年冬至点离太阳近地点较远的缘故。郭守敬当年两者很接近,因此即使以冬至前后60天的数据进行推算,其误差也在3刻以内,而2014年以冬至前后60天的数据进行推算,误差会达到20刻以上。所以,郭守敬推算冬至时刻的精准不仅仅得益于他对影长的精确测量,也得益于当时冬至点正好与太阳近地点接近的有利条件,可以说是有相当大的“运气”成份。

最后对《元史·历志》“授时历议”中所载的影长数据和冬至时刻进行分析,发现《授时历》推算冬至时刻,并不是采用了影长数据所能提供的所有可能推算组合,而是有所取舍。郭守敬只选择冬至时刻在“后一刻以内”的推算组合,对于超出这个“标准”的组合,则完全不提,人为选择的倾向很明显。

致 谢 本文的实测工作中,北京古观象台肖军台长提供了测影场地和仪器,特此感谢。

1 陈美东. 论我国古代冬至时刻的测定及郭守敬等人的贡献[J]. 自然科学史研究, 1983, 2(1): 51—60.

2 陈美东. 郭守敬等人晷影测量结果的分析[J]. 天文学报, 1982, 23(3): 299—305.

3 李勇. 中国古代太阳中天观测及二至点测算精度[J]. 天文学进展, 2005, 23(1): 70—79.

4 李勇. 《授时历》历元时刻的获取[J]. 天文学报, 2013, (6): 569—580.

5 郭盛炽, 全和钧, 张家泰等. 古观星台测景结果精度分析[J]. 自然科学史研究, 1983, 2(2): 139—144.

6 陈美东. 中国科学技术史·天文学卷[M]. 北京: 科学出版社, 2003.

7 Sun, Xiaochun, Jacob, Kistemaker. Influence of Islamic Astronomy in Song and Yuan China Some facts and Discussions[J].ProceedingsoftheXXthInternationalCongressofHistoryandScience, 2001, (9): 59—74.

8 Hartner, W. The Astronomical Instruments of Cha-Ma-Lu-Ting, their Identification, and their Relations to the Instruments of the Observatory of Maragha. [J].ISIS, 1950, (41): 184.

9 (宋)苏颂. 陆敬严, 钱学英译. 新仪象法要译注[M]. 上海: 上海古籍出版社, 2007.

10 (明)宋濂, 等. 元史[M]. 北京: 中华书局, 1974.

11 薄树人. 试探有关郭守敬仪器的几个悬案[J]. 自然科学史研究, 1982, 1(4): 320—326.

12 伊世同. 元代圭表复原探索[J]. 自然科学史研究, 1984, 3(2): 128—137.

13 丘光明. 中国古代度量衡[M]. 北京: 商务印书馆, 1996.

14 崔石竹, 李东生. 仿古测影探索[J]. 自然科学史研究, 1987, 6(4): 332—341.

15 黎耕, 孙小淳. 陶寺IIM22漆杆与圭表测影[J]. 中国科技史杂志, 2010, (4): 363—372.

16 (梁)沈约. 宋书[M]. 北京: 中华书局, 1974. 313.

A Simulative Study of Guo Shoujing’s Determination of the Winter Solstice using a Gnomon

XIAO Yao SUN Xiaochun

(School of Humanities, University of Chinese Academy of Sciences, Beijing 100049, China)

In the beginning of the Yuan Dynasty, for the determination of the moment of Winter Solstice, Guo Shoujing constructed the 40-chi-high gnomon and shadow definer, which increased the accuracy considerably. This paper studies Guo Shoujing’s method of determining Winter Solstice and its accuracy by means of simulative measurement. Using the 8-chi-high gnomon at Beijing Ancient Observatory, we measured the noon shadow lengths for a period of 33 days around the winter solstice day of 2014. Applying Guo Shoujing’s method, we are able to determine the moment of Winter Solstice of 2014. Comparing our simulative result for 2014 with Guo Shoujing’s result of 1277—1279, we analyze the reason why Guo Shoujing could obtain high accuracy in his determination of Winter Solstice. We discover that, for calculation, Guo Shoujing had been very selective in using the original data of gnomon measurement in order to produce the desired results for theShoushili.

Gnomon shadow measurement, Guo Shoujing,Shoushili, Simulative measurement, Winter Solstice

2016- 05- 18；

2016- 08- 20

肖尧,1990年生,江苏仪征人,中国科学院大学2016级科学技术史专业博士研究生,研究方向为天文学史；孙小淳,1964年生,江苏溧阳人,中国科学院大学教授,研究方向天文学史。

N092∶P1- 092

A

1673- 1441(2016)04- 0397- 16