将构造函数进行到底
2016-09-06安徽省合肥市第十七中学
安徽省合肥市第十七中学
杨维维 (邮编:230011)
将构造函数进行到底
安徽省合肥市第十七中学
杨维维(邮编:230011)
高考中含参数导数题,不管是选择、填空题还是解答题,学生往往难以找到有效的突破口,或者一遇到此类问题就分离参数,有的可以解决,有的造成计算量大且难以进行.此类问题的求解有两种基本思路:可以分离参数再构造函数,也可以直接构造函数.对于直接构造函数的情形,我们可构造一个函数,也可构造两个函数.
1 构造函数 因法而异
例1(2013年湖北省高考数学理科第10题)
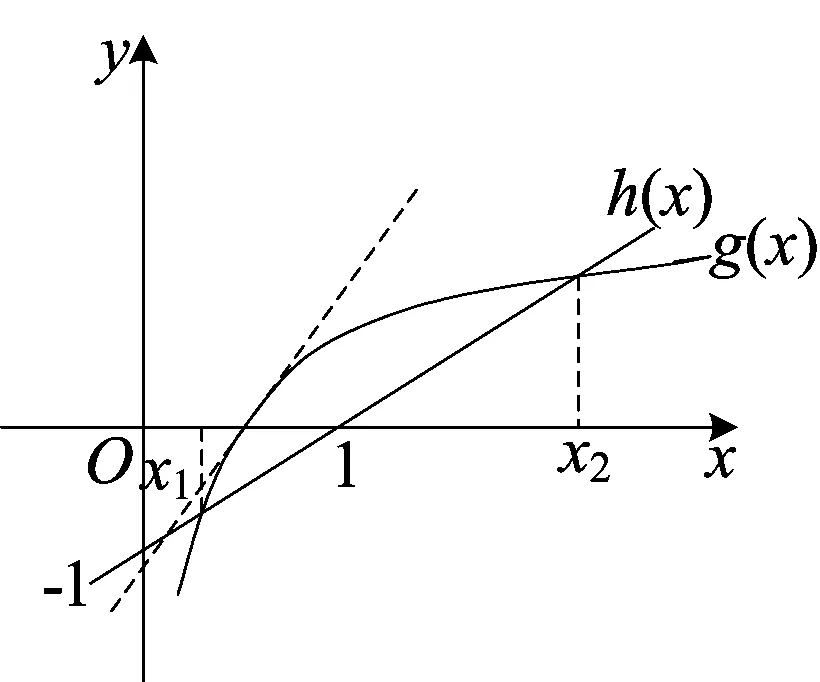
已知a为常数,函数f(x)=xlnx-ax2有两极值点x1、x2(x1 思路一求导后,分离参数再构造函数 解法一 由于f(x)=xlnx-ax2x有两个极值点x1、x2(x1 f′(x)=lnx-2ax+1有两个零点x1、x2, (0,x1)x1(x1,x2)x2(x2,+∞)f'(x)-0+0—f(x)↘极小值↗极大值↘ 解法二f′(x)=lnx-2ax+1(x>0)有两个零点x1、x2. 令f′(x)=0,由题意可得lnx=2ax-1有两个解x1、x2,即g(x)=lnx与 h(x)=2ax-1 在(0,+∞)上有两个交点. 由图象得 a>0,且0 思路三求导后,构造一个含参数函数,进行二次求导 所以y=g(x)至多有一个零点,不符合题意,舍去. 例2 (2016年高考数学全国卷I理科第21题) 已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. (I)求a的取值范围;(II)略. 解 (I) 法一分离参数再构造函数 当x=1时,f(1)=-e,故x=1不是零点. 所以g(x)在(-∞,1)内单调递减,在(1,+∞)内单调递增. 又g(2)=0,当x∈(-∞,1)时,g(x)<0,又x趋向于1时,g(x)趋向于-∞,x趋向于-∞时,g(x)趋向于0,若函数f(x)有两个零点,则需-a<0,即a>0. 法二变形后构造两个函数 设f(x)=(x-2)ex+a(x-1)2=0,得(2-x)ex=a(x-1)2, 令g(x)=(2-x)ex,得g′(x)=(1-x)ex,当x∈(-∞,1)时,g′(x)>0;当x∈(1,+∞)时,g′(x)<0,所以g(x)在(-∞,1)单调递增,在(1,+∞)单调递减,则在x=1处取得极大值g(1)=e. 又x<1时,g(x)=(2-x)ex>0,x=3时,g(x)=-e3<0,又设h(x)=a(x-1)2,知: ①当a>0时,h(x)=a(x-1)2为开口朝上的抛物线,顶点为(1,0),所以函数f(x)有两个零点; ②当a=0时,h(x)=a(x-1)2为x轴,所以函数f(x)有一个零点; ③当a<0时,h(x)=a(x-1)2为开口朝下的抛物线,顶点为(1,0),所以函数f(x)不可能有两个零点. 综上,a的取值范围为(0,+∞). 法三直接利用已知函数,讨论函数单调性 f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a). ①设a=0,则f(x)=(x-2)ex,所以f(x)有一个零点; ②设a>0,则当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,所以f(x)在(-∞,1)内单调递减,在(1,+∞)内单调递增. ③设a<0,由f′(x)=0得x=1或x=ln(-2a). 又当x≤1时,f(x)<0,故f(x)不存在两个零点. 比较三种方法,本题法一较简便. 例3(2016年合肥市二模理科第21题) 已知函数g(x)=ax3+x2+x (a为实数). (1)试讨论函数 g(x)的单调性; 解 (1)略; 当a>-1时,g(1)=a+2>1=f(1),显然,对∀x∈(0,+∞),不恒有f(x)≥g(x); 综上,实数a∈(-∞,-1]. 解题教学应立足通性通法,并不断优化提炼解法.分离参数后构造函数和变形后构造两个函数都要求构造出来的函数形式上简洁,便于判断单调性,而直接构造一个含参数的函数,往往需要对参数分类讨论,判断函数的单调性,究竟采用哪种方法好?应结合题目的具体特点,因题制宜,进行合理选择,灵活变通,在高考中方能百战不殆. 2016-06-16)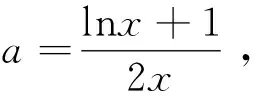

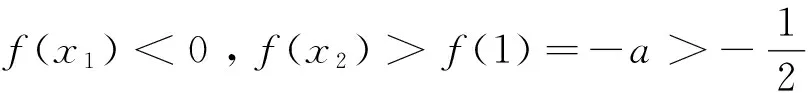



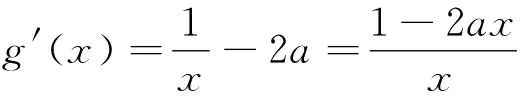





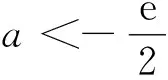

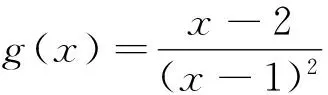
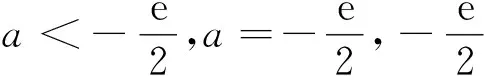
2 构造函数 合理选择




