基于灵敏度的SUV车架多性能综合优化
2016-09-06欧贺国马忠民汤晓东OuHeguoMaZhongminTangXiaodong北京汽车越野车研究院整车集成与CAE部北京100131
欧贺国,马忠民,汤晓东Ou Heguo,Ma Zhongmin,Tang Xiaodong(北京汽车越野车研究院 整车集成与CAE部,北京 100131)
基于灵敏度的SUV车架多性能综合优化
欧贺国,马忠民,汤晓东
Ou Heguo,Ma Zhongmin,Tang Xiaodong
(北京汽车越野车研究院整车集成与CAE部,北京100131)
建立某SUV车架的有限元模型,对车架进行弯曲刚度、扭转刚度和模态分析,并进行车架的弯曲和扭转刚度测试,测试结果验证了有限元模型的准确性。按照质量敏感度因子排序确定车架主要构件的优化对象,包括零件料厚和纵梁截面尺寸,并建立多目标优化模型。在提升弯扭刚度和低阶频率达到设计目标的同时,降低车架的总质量,达到轻量化设计的目标。
多目标优化;轻量化;灵敏度;车架
0 引 言
SUV经常行驶在各种复杂路况,在行驶中受到弯曲、扭转等多种载荷。作为非承载式SUV的主要承载部件,车架需要具有良好的刚度和强度,同时为了保证乘坐舒适性和使用寿命,车架还需具有良好的动态特性。作为提高燃油经济性和减少排放的有效手段之一,轻量化结构设计在汽车开发中成为一种设计要求和技术手段。SUV车架是连接车身与悬架的主要承载部件,全尺寸非承载式SUV车架总质量通常达到250~300 kg,在整车总质量中占有较大比重,因此在车架设计中需要考虑轻量化要求。
传统的多目标优化问题采用线性加权法将多目标问题转化为单目标问题进行求解,但其缺点很明显,权重的选择和各个目标的相对重要程度有很大关系,此外在搜索空间非凸时,该方法不能确保得到所有Pareto最优解[1,5]。另一种常用的多目标优化方法折衷规划法[2-4]在计算时同时考虑设计变量对多个目标的影响,通过折衷选择优化数值将多目标优化问题转化为单目标问题,以保证多个目标同时达到折衷的优化解。遗传算法在求解多目标问题上的应用越来越多,但其解决约束优化问题还缺乏有效的手段,多目标优化问题的有效求解目标数一般不超过 4个,且计算量很大[5]。ε-约束法[6-8]求解是将多目标问题的某一个目标函数作为优化目标,而约束其他目标函数,将多目标优化问题转换成单目标优化问题,转换成约束条件的目标函数只在Pareto最优边界上取值。
以某SUV车架为对象,对车架的基础设计进行了弯扭刚度和低阶频率的有限元分析,并用车架刚度测试的结果验证了有限元模型的准确性。为减少设计变量和提升运算效率,根据设计变量相对于总质量的敏感度排序以及潜在的结构耐久性能、碰撞安全性能和总布置的要求,筛选出25个零件的料厚、纵梁主截面尺寸和第五横梁截面尺寸作为优化模型的设计变量,按照 ε-约束法将车架弯曲刚度、扭转刚度、一阶扭转频率和一阶弯曲频率这4个设计目标转换为约束条件,以车架总质量最小为目标,将多目标优化问题转换成单目标问题,使用可行方向法进行优化迭代,优化收敛的设计方案中弯扭刚度和弯扭频率均满足设计目标值,车架总质量比设计要求减少8.43%,最终得到满足刚度和模态要求的车架轻量化设计方案。
1 车架刚度及模态有限元分析
1.1车架有限元模型
以平均尺寸8 mm来划分车架钣金零件网格单元,以平均尺寸5 mm对排气吊钩等实体棒形零件进行实体单元划分,焊缝采用连续的刚性单元RBE2建模,得到完整的车架有限元模型。模型中四边形单元182 517个,三角形单元5 200个,六面体单元5 040个,节点总数205 471个。通过微调所赋材料属性的密度值,得到总质量263 kg(不含前保险杠横梁系统),与实际车架质量一致,有限元模型如图1所示。
1.2车架刚度、模态分析和试验验证
按车架刚度测试规范,在车架有限元模型上进行弯曲、扭转刚度和模态计算。为验证有限元模型的准确性,同步展开对基础车架的刚度测试,有限元分析和试验测试的结果见表1。

表1 计算所得车架弯扭刚度和低阶自然频率
刚度测试结果和模型分析结果的偏差小于5%,可见当前有限元模型具有很高的准确性。表1同时列出了车架的设计目标,初始设计与设计目标尚有较大差距。
2 多性能目标综合优化模型
2.1灵敏度分析
设计灵敏度就是结构响应对设计变量的偏导数,也即结构响应的梯度。有限元方程
其中,K为刚度矩阵,U为单元节点位移向量,P为单元节点载荷向量。
方程两边对设计变量X求偏导数并对刚度矩阵求逆变换
将结构响应(如约束函数g)描述为位移向量U的函数
结构响应的灵敏度为
其中,Q为结构响应g的伴随载荷矩阵。
按左右对称关系对车架所有钣金零件的料厚属性进行压缩合并后,共有80个料厚属性。计算这些料厚属性对车架总质量、弯曲刚度、扭转刚度、一阶扭转频率、一阶弯曲频率的灵敏度,并分别进行排序作为设计变量选取的初始依据。限于篇幅,仅在表2列出待优化的25个料厚属性的灵敏度。
2.2设计变量的确定
车身悬置支架、前后悬架减振器支座、后悬架横向推力杆支架、尾横梁硬拖挂支架等零部件有较高耐久性能要求,纵梁前端及前保险杠横梁安装支架对整车碰撞性能影响极大,前部水箱横梁沿用其他车型,这些系统不允许设计变更,故不将这些零件纳入考查范围。相对于零件料厚的调整,车架纵梁和横梁的截面尺寸对其整体性能影响更为显著,但工程实际中车架主截面尺寸的变化需要全方位考虑整车通过性能、子系统之间布置间隙、开发成本等因素,经反复协调和估算,此车架主截面可用设计空间是纵梁中部最大向外加宽10 mm,第五横梁下板最大向下加高5 mm。经上述平衡与综合,最终确定25个料厚设计变量和2个形状设计变量,如图2所示,阴影显示了零件及截面变化。
表2和图3列出了27个设计变量相对于5个设计目标的响应灵敏度。灵敏度为正,表示该响应随变量的增大而增大,反之则表示该响应随变量的增大而减小。

表2 设计变量灵敏度列表
2.3多目标优化模型
按整车性能目标的分解要求,如表 1所示,此车架的基本性能指标(弯扭刚度和频率)与设计目标存在较大差距,参考竞争车型的情况,改进后的车架质量要求低于320 kg(不含前保险杠横梁)。观察表2所示的灵敏度,注意到其中的部分设计的增大对五种响应引起的变化是互相矛盾的,这构成了典型的非一致多目标优化问题。
按照ε-约束法将车架质量最小值设为优化目标,将车架弯扭频率和刚度目标转换为约束条件,建立优化数学模型
式中,f(X)为目标函数,车架质量;Freq_T0为扭转频率目标值,25 Hz;Freq_B0为弯曲频率目标值,29 Hz;Stiff_T0为扭转刚度目标值,5 000 N·m/ (°);Stiff_B0为弯曲刚度目标值,4 700 N/mm;xi为料厚和截面形状因子。
考虑到实际板材可选用的料厚规格,设置料厚变量的离散取值为:1.5,1.6,1.8,2.0,2.2,2.5,2.8,3.0,3.2,3.5,3.8,4.0,4.5,5.0 mm;同时将截面形状因子变量(第7和第27号变量)设为离散型变量,最小变动量是0.1 mm,对应纵梁截面向外加宽 1 mm和第五横梁截面向下加高0.5 mm。
3 优化结果
3.1优化计算
在针对频率进行结构优化的工程实际中,经常会出现频率阶次的跳变问题,即当结构发生变化时其固有频率阶次分布也会发生互相调换次序的情况,为避免此问题干扰频率响应约束,在OptiStruct中对优化模型的求解施加模态追踪控制[9],以确保25 Hz的频率约束只对其第一个整体扭转振型的频率进行限制,29 Hz的频率约束只对其第一个整体弯曲振型的频率进行限制。经过 8次迭代后,优化模型得到收敛解,车架的弯扭频率和刚度均满足约束要求。车架质量、频率和刚度的迭代曲线如图4—图6所示。
3.2优化结果
通过多目标优化,所有的优化目标都达到了优化要求。27个设计变量的初始值和最终优化值见表3,车架基本性能综合优化前后的对比见表4。
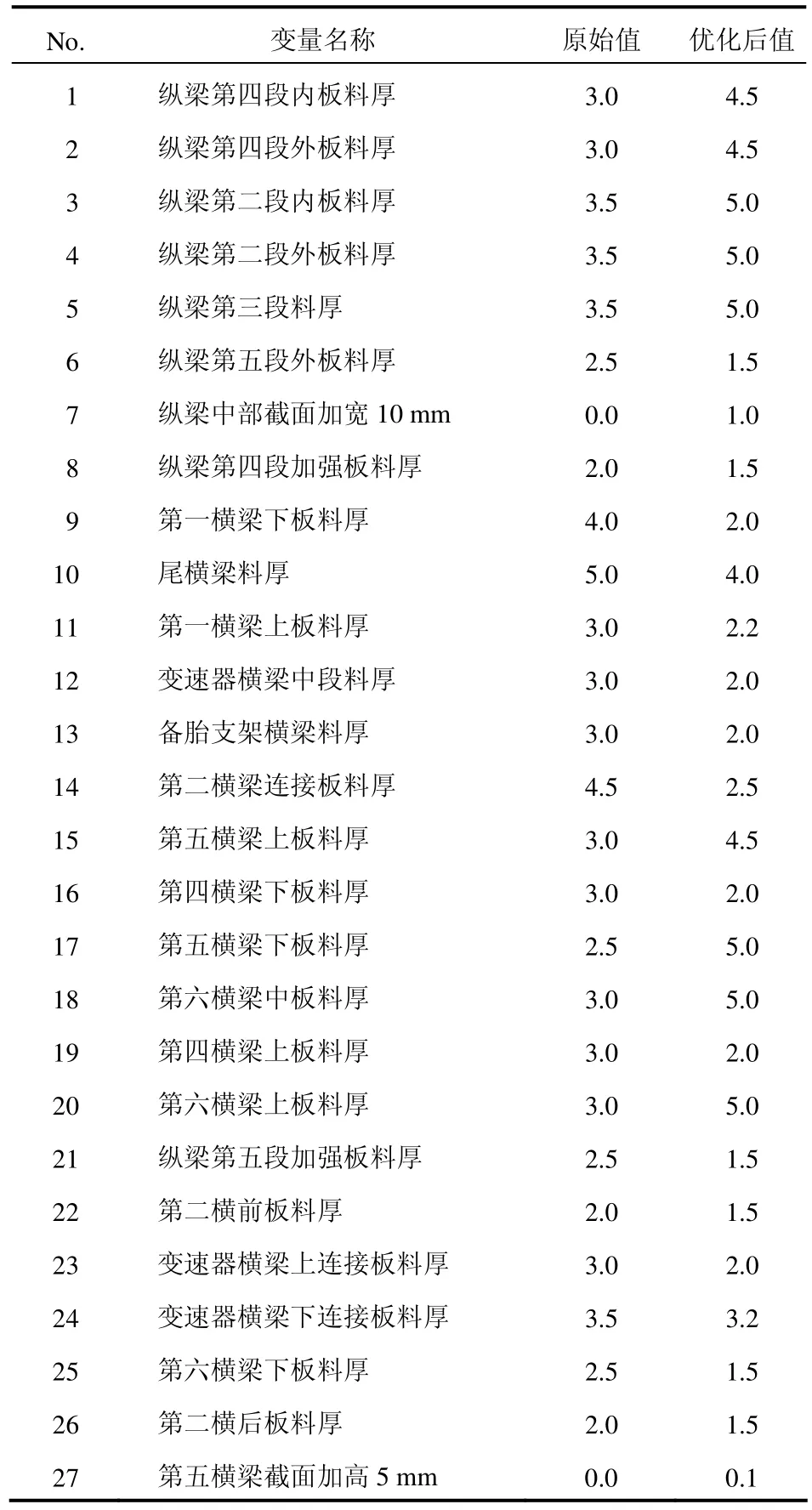
表3 设计变量优化结果
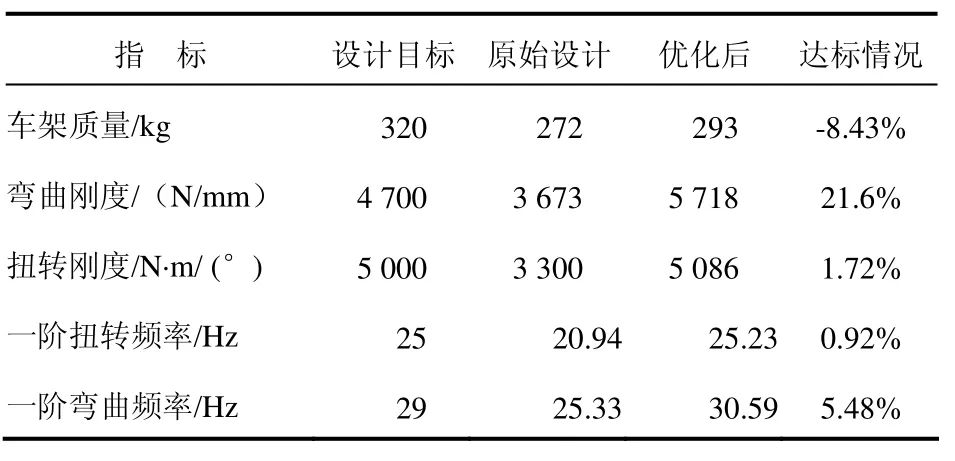
表4 车架基本性能优化前后对比
由表 4可知,优化后的车架质量有所上升,但仍然比设计目标减轻8.43%,弯扭刚度和频率均高于设计目标;因此,优化后的设计是一个满足刚度和模态要求的车架轻量化设计方案。
4 结束语
基于刚度测试验证的SUV车架有限元模型,采用灵敏度分析排序确定车架多性能提升的设计变量,按 ε-约束法将车架质量最小值设为优化目标,将车架弯扭频率和刚度目标转换为约束条件,创建了多目标优化模型。迭代收敛的车架设计方案的弯扭刚度和频率有大幅度提升,达到了实际要求,车架的质量比设计目标减轻8.43%,最终得到了满足刚度和模态要求的车架轻量化设计方案。
[1]Marler R T, Arora J S.Survey of Multi-objective Optimization Methods for Engineering [J].Struct.Multidisc.Optim., 2004, 26 (6): 369-395.
[2]刘江,桂良进,王青春,等.全承载式大客车车身结构多目标优化[J].汽车工程,2008,30(2):170-173.
[3]向湘林,左孔天,向宇,等.某 SUV 车架多目标拓扑优化设计[J].计算机辅助工程,2012,21(5):20-24.
[4]CHEN T Y, WU S C.Multiobjective Optimal Topology Design of Structures [J].Computional Mechanics, 1998, 21(6): 483-492.
[5]马小姝,李宇龙,严浪.传统多目标优化方法和多目标遗传算法的比较综述[J].电气传动自动化,2010,32(3):48-50.
[6]Marglin S.Public Investment Criteria[M].MIT Press, Cambridge, Massachusetts, 1967.
[7]Haimes Y Y.Integrated System Identification and Optimization [J].Control and Dynamic Systems, 1973, 10: 435-518.
[8]George Mavrotas.Effective Implementation of the ε-constraint Method in Multi-objective Mathematical Programming Problems[J].Applied Mathematics and Computation, 2009, 213 (2).455-465.
[9]Altair Engineering Inc.Altair OptiStruct Reference Manual[Z].2014.
U463.82: TP391.9
A
10.14175/j.issn.1002-4581.2016.04.002
1002-4581(2016)04-0004-05
2016-03-04--
